Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

V.3 Landau-Ginzburg Theory of Critical Phenomena

The emergence of nonanalyticity

Historically, the notion of spontaneous symmetry breaking, originating in the work of

Landau and Ginzburg on second-order phase transitions, came into particle physics from

condensed matter physics.

Consider a ferromagnetic material in thermal equilibrium at temperature T . The mag-

netization



M(x) is defined as the average of the atomic magnetic moments taken over

a region of a size much larger than the length scale characteristic of the relevant micro-

scopic physics. (In this chapter, we are discussing a nonrelativistic theory and x denotes the

spatial coordinates only.) We know that at low temperatures, rotational invariance is spon-

taneously broken and that the material exhibits a bulk magnetization pointing in some

direction. As the temperature is raised past some critical temperature T

the bulk mag-

netization suddenly disappears. We understand that with increased thermal agitation the

atomic magnetic moments point in increasingly random directions, canceling each other

out. More precisely, it was found experimentally that just below T

the magnetization |



vanishes as ∼ (T

− T)

, where the so-called critical exponent β  0.37.

This sudden change is known as a second order phase transition, an example of a

critical phenomenon. Historically, critical phenomena presented a challenge to theoretical

physicists. In principle, we are to compute the partition function Z = tr e

−H/T

with

the microscopic Hamiltonian H, but Z is apparently smooth in T except possibly at

T = 0. Some physicists went as far as saying that nonanalytic behavior such as (T

−

is impossible and that within experimental error |



M| actually vanishes as a smooth

function of T . Part of the importance of Onsager’s famous exact solution in 1944 of the 2-

dimensional Ising model is that it settled this question definitively. The secret is that an

infinite sum of terms each of which may be analytic in some variable need not be analytic

in that variable. The trace in tr e

−H/T

sums over an infinite number of terms.

V.3. Theory of Critical Phenomena | 293

Arguing from symmetry

In most situations, it is essentially impossible to calculate Z starting with the microscopic

Hamiltonian. Landau and Ginzburg had the brilliant insight that the form of the free

energy G as a function of



M for a system with volume V could be argued from general

principles. First, for



M constant in x , we have by rotational invariance

G = V [a



+ b(



)

...

] (1)

where a, b,

...

are unknown (but expected to be smooth) functions of T. Landau and

Ginzburg supposed that a vanishes at some temperature T

. Unless there is some special

reason, we would expect that for T near T

we have a = a

(T − T

) +

...

[rather than, say,

a = a

(T − T

)

...

]. But you already learned in chapter IV.1 what would happen. For

T>T

, G is minimized at



M =0, but as T drops below T

, new minima suddenly develop

at |



M|=



(−a/2b) ∼ (T

− T)

. Rotational symmetry is spontaneously broken, and the

mysterious nonanalytic behavior pops out easily.

To include the possibility of



M varying in space, Landau and Ginzburg argued that G

must have the form

G =



x{∂



M∂



M + a



+ b(



)

...

} (2)

where the coefficient of the (∂



term has been set to 1 by rescaling



M. You would

recognize (2) as the Euclidean version of the scalar field theory we have been studying. By

dimensional analysis we see that 1/

√

a sets the length scale. More precisely, for T>T

let us turn on a perturbing external magnetic field



H(x) by adding the term −



Assuming



M small and minimizing G we obtain (−∂

+ a)



M 



H , with the solution



M(x) =



(2π)



(x−y)



+ a



H(y)



4π |x −y|

−

√

a|x−y|



H(y) (3)

[Recall that we did the integral in (I.4.7)—admire the unity of physics!]

It is standard to define a correlation function <



M(x)



M(0)>by asking what the mag-

netization



M(x) will be if we use a magnetic field sharply localized at the origin to create

a magnetization



M(0) there. We expect the correlation function to die off as e

−|x|/ξ

over

some correlation length ξ that goes to infinity as T approaches T

from above. The critical

exponent ν is traditionally defined by ξ ∼ 1/(T − T

)

In Landau-Ginzburg theory, also known as mean field theory, we obtain ξ = 1/

√

a and

hence ν =

The important point is not how well the predicted critical exponents such as β and ν

agree with experiment but how easily they emerge from Landau-Ginzburg theory. The

theory provides a starting point for a complete theory of critical phenomena, which was

eventually developed by Kadanoff, Fisher, Wilson, and others using the renormalization

group (to be discussed in chapter VI.8).

294 | V. Field Theory and Collective Phenomena

The story goes that Landau had a logarithmic scale with which he ranked theoretical

physicists, with Einstein on top, and that after working out Landau-Ginzburg theory he

moved himself up by half a notch.

Exercise

V.3.1 Another important critical exponent γ is defined by saying that the susceptibility χ ≡ (∂M/∂H)|

H =0

diverges ∼1/|T −T

as T approaches T

. Determine γ in Landau-Ginzburg theory. [Hint: Instructively,

there are two ways of doing it: (a) Add −



M to (1) for



M and



H constant in space and solve for



H).

(b) Calculate the susceptibility function χ

(x − y) ≡ [∂M

(x)/∂H

(y)]|

H =0

and integrate over space.]

V.4 Superconductivity

Pairing and condensation

When certain materials are cooled below a certain critical temperature T

, they suddenly be-

come superconducting. Historically, physicists had long suspected that the superconduct-

ing transition, just like the superfluid transition, has something to do with Bose-Einstein

condensation. But electrons are fermions, not bosons, and thus they first have to pair

into bosons, which then condense. We now know that this general picture is substantially

correct: Electrons form Cooper pairs, whose condensation is responsible for superconduc-

tivity.

With brilliant insight, Landau and Ginzburg realized that without having to know the

detailed mechanism driving the pairing of electrons into bosons, they could understand

a great deal about superconductivity by studying the field ϕ(x) associated with these con-

densing bosons. In analogy with the ferromagnetic transition in which the magnetization



M(x) in a ferromagnet suddenly changes from zero to a nonzero value when the temper-

ature drops below some critical temperature, they proposed that ϕ(x) becomes nonzero

for temperatures below T

. (In this chapter x denotes spatial coordinates only.) In statisti-

cal physics, quantities such as



M(x) and ϕ(x) that change through a phase transition are

known as order parameters.

The field ϕ(x) carries two units of electric charge and is therefore complex. The dis-

cussion now unfolds much as in chapter V.3 except that ∂

ϕ should be replaced by D

ϕ ≡

(∂

−i2eA

)ϕ since ϕ is charged. Following Landau and Ginzburg and including the energy

of the external magnetic field, we write the free energy as

F =

+|D

ϕ|

+ a|ϕ|

|ϕ|

...

(1)

which is clearly invariant under the U(1) gauge transformation ϕ → e

i2e

ϕ and A

→A

∂

. As before, setting the coefficient of |D

ϕ|

equal to 1 just amounts to a normalization

choice for ϕ.

The similarity between (1) and (IV.6.1) should be evident.

296 | V. Field Theory and Collective Phenomena

Meissner effect

A hallmark of superconductivity is the Meissner effect, in which an external magnetic

field



B permeating the material is expelled from it as the temperature drops below T

. This

indicates that a constant magnetic field inside the material is not favored energetically. The

effective laws of electromagnetism in the material must somehow change at T

. Normally,

a constant magnetic field would cost an energy of the order ∼



V , where V is the volume

of the material. Suppose that the energy density is changed from the standard



(where as usual



∇×



A =



B). For a constant magnetic field



A grows as the distance and

hence the total energy would grow faster than V . After the material goes superconducting,

we have to pay an unacceptably large amount of extra energy to maintain the constant

magnetic field and so it is more favorable to expel the magnetic field.

Note that a term like



in the effective energy density preserves rotational and transla-

tional invariance but violates electromagnetic gauge invariance. But we already know how

to break gauge invariance from chapter IV.6. Indeed, the U(1) gauge theory described there

and the theory of superconductivity described here are essentially the same, related by a

Wick rotation.

As in chapter V.3 we suppose that for temperature T  T

, a  a

(T − T

) while b

remains positive. The free energy F is minimized by ϕ = 0 above T

, and by |ϕ|=

√

−a/b ≡ v below T

. All this is old hat to you, who have learned that upon symmetry

breaking in a gauge theory the gauge field gains a mass. We simply read off from (1) that

F =

+ (2ev)

...

(2)

which is precisely what we need to explain the Meissner effect.

London penetration length and coherence length

Physically, the magnetic field does not drop precipitously from some nonzero value outside

the superconductor to zero inside, but drops over some characteristic length scale, called

the London penetration length. The magnetic field leaks into the superconductor a bit over

a length scale l, determined by the competition between the energy in the magnetic field

∼ (∂A)

∼ A

and the Meissner term (2ev)

in (2). Thus, Landau and Ginzburg

obtained the London penetration length l

∼ (1/ev) = (1/e)

√

b/−a.

Similarly, the characteristic length scale over which the order parameter ϕ varies is

known as the coherence length l

, which can be estimated by balancing the second and

third terms in (1), roughly (∂ϕ)

∼ ϕ

and aϕ

against each other, giving a coherence

length of order l

∼ 1/

√

−a.

Putting things together, we have

∼

√

(3)

V.4. Superconductivity | 297

You might recognize from chapter IV.6 that this is just the ratio of the mass of the scalar

field to the mass of the vector field.

As I remarked earlier, the concept of spontaneous symmetry breaking went from con-

densed matter physics to particle physics. After hearing a talk at the University of Chicago

on the Bardeen-Cooper-Schrieffer theory of superconductivity by the young Schrieffer,

Nambu played an influential role in bringing spontaneous symmetry breaking to the par-

ticle physics community.

Exercises

V.4.1 Vary (1) to obtain the equation for A and determine the London penetration length more carefully.

V.4.2 Determine the coherence length more carefully.

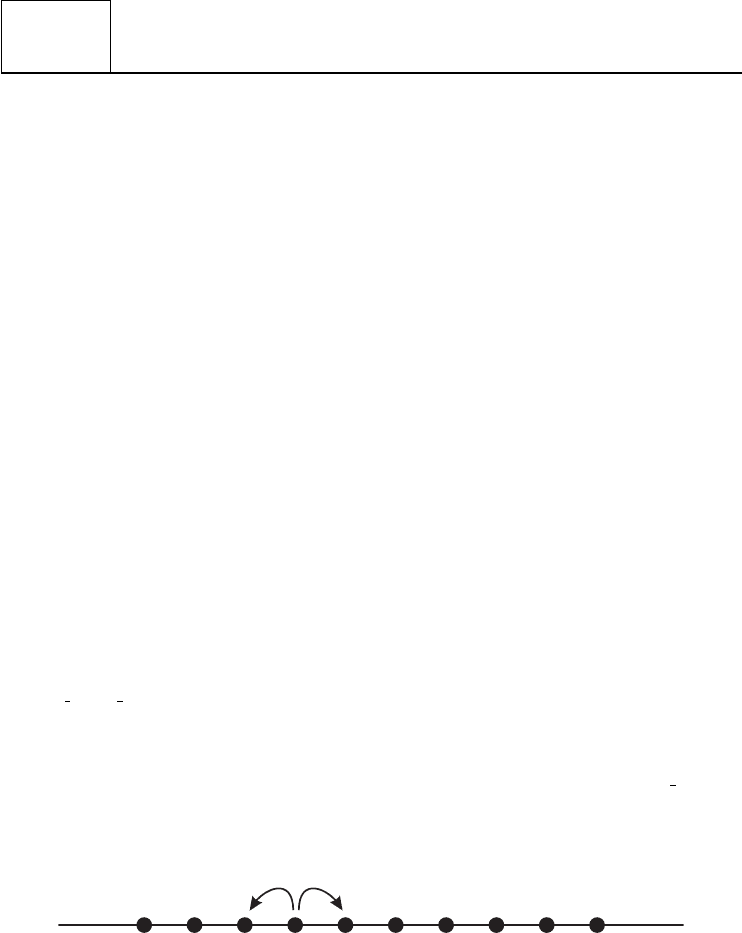
V.5 Peierls Instability

Noninteracting hopping electrons

The appearance of the Dirac equation and a relativistic field theory in a solid would be

surprising indeed, but yes, it is possible.

Consider the Hamiltonian

H =−t



†

j+1

+ c

†

j+1

) (1)

describing noninteracting electrons hopping on a 1-dimensional lattice (figure V.5.1). Here

annihilates an electron on site j . Thus, the first term describes an electron hopping from

site j to site j +1 with amplitude t . We have suppressed the spin labels. This is just about

the simplest solid state model; a good place to read about it is in Feynman’s “Freshman

lectures.”

Fourier transforming c



ikaj

c(k) (where a is the spacing between sites), we

immediately find the energy spectrum ε(k) =−2t cos ka (fig. V.5.2). Imposing a periodic

boundary condition on a lattice with N sites, we have k = (2π/Na)n with n an integer

from −

N to

N .AsN →∞, k becomes a continuous rather than a discrete variable. As

usual, the Brillouin zone is defined by −π/a < k ≤ π/a.

There is absolutely nothing relativistic about any of this. Indeed, at the bottom of the

spectrum the energy (up to an irrelevant additive constant) goes as ε(k)  2t

(ka)

≡

/2m

eff

. The electron disperses nonrelativistically with an effective mass m

eff

jj + 1j − 1

Figure V.5.1

V.5. Peierls Instability | 299

ε(k)

Figure V.5.2

But now let us fill the system with electrons up to some Fermi energy ε

(see fig.

V.5.2). Focus on an electron near the Fermi surface and measure its energy from ε

and momentum from +k

. Suppose we are interested in electrons with energy small

compared to ε

, that is, E ≡ ε − ε

ε

, and momentum small compared to k

, that is,

p ≡ k − k

 k

. These electrons obey a linear energy-momentum dispersion E = v

with the Fermi velocity v

= (∂ε/∂k)|

k=k

. We will call the field associated with these

electrons ψ

, where the subscript indicates that they are “right moving.” It satisfies the

equation of motion (∂/∂t + v

∂/∂x)ψ

= 0.

Similarly, the electrons with momentum around −k

obey the dispersion E =−v

We will call the field associated with these electrons ψ

with L for “left moving,” satisfying

(∂/∂t − v

∂/∂x)ψ

= 0.

Emergence of the Dirac equation

The Lagrangian summarizing all this is simply

L = iψ

†



∂

∂t

+ v

∂

∂x



+ iψ

†



∂

∂t

− v

∂

∂x



(2)

Introducing a 2-component field ψ =





ψ ≡ψ

†

≡ ψ

†

, and choosing units so

that v

= 1, we may write L more compactly as

L = iψ

†



∂

∂t

− σ

∂

∂x



ψ =

ψiγ

∂

ψ (3)

with γ

= σ

and γ

= iσ

satisfying the Clifford algebra {γ

, γ

}=2g

μν

300 | V. Field Theory and Collective Phenomena

Amazingly enough, the (1 + 1)-dimensional Dirac Lagrangian emerges in a totally

nonrelativistic situation!

An instability

I will now go on to discuss an important phenomenon known as Peierls’s instability. I will

necessarily have to be a bit sketchy. I don’t have to tell you again that this is not a text on

solid state physics, but in any case you will not find it difficult to fill in the gaps.

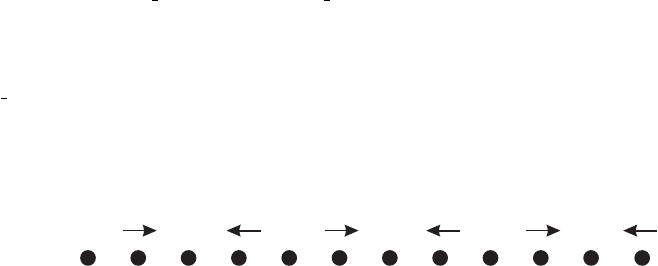
Peierls considered a distortion in the lattice, with the ion at site j displaced from its

equilibrium position by cos[q(ja)]. (Shades of our mattress from chapter I.1!) A lattice

distortion with wave vector q = 2k

will connect electrons with momentum k

with

electrons with momentum −k

. In other words, it connects right moving ones with

left moving electrons, or in our field theoretic language ψ

with ψ

. Since the right

moving electrons and the left moving electrons on the surface of the Fermi sea have the

same energy (namely ε

, duh!) we have the always interesting situation of degenerate

perturbation theory:



0 ε





0 δ

δ 0



with eigenvalues ε

±δ. A gap opens at the surface

of the Fermi sea. Here δ represents the perturbation. Thus, Peierls concluded that the

spectrum changes drastically and the system is unstable under a perturbation with wave

vector 2k

A particularly interesting situation occurs when the system is half filled with electrons

(so that the density is one electron per site—recall that electrons have up and down spin).

In other words, k

= π/2a and thus 2k

= π/a. A lattice distortion of the form shown in

figure V.5.3 has precisely this wave vector. Peierls showed that a half-filled system would

want to distort the lattice in this way, doubling the unit cell. It is instructive to see how this

physical phenomenon emerges in a field theoretic formulation.

Denote the displacement of the ion at site j by d

. In the continuum limit, we should be

able to replace d

by a scalar field. Show that a perturbation connecting ψ

and ψ

couples

ψψ and

ψγ

ψ, and that a linear combination

ψψ and

ψγ

ψ can always be rotated to

ψψ by a chiral transformation (see exercise V.5.1.) Thus, we extend (3) to

L =

ψiγ

∂

ψ +

[(∂

ϕ)

− v

(∂

ϕ)

] −

+ gϕ

ψψ +

...

(4)

Remember that you worked out the effective potential V

eff

(ϕ) of this (1 + 1)-dimensional

field theory in exercise IV.3.2: V

eff

(ϕ) goes as ϕ

log ϕ

for small ϕ, which overwhelms the

term. Thus, the symmetry ϕ →−ϕ is dynamically broken. The field ϕ acquires a

vacuum expectation value and ψ becomes massive. In other words, the electron spectrum

develops a gap.

Figure V.5.3

V.5. Peierls Instability | 301

Exercise

V.5.1 Parallel to the discussion in chapter II.1 you can see easily that the space of 2 by 2 matrices is spanned by

the four matrices I , γ

, and γ

≡ γ

= σ

. (Note the peculiar but standard notation of γ

.) Convince

yourself that

(I ±γ

) projects out right- and left handed fields just as in (3 + 1)-dimensional spacetime.

Show that in the bilinear

ψγ

ψ left handed fields are connected to left handed fields and right handed

to right handed and that in the scalar

ψψ and the pseudoscalar

ψγ

ψ right handed is connected to

left handed and vice versa. Finally, note that under the transformation ψ →e

iθγ

ψ the scalar and the

pseudoscalar rotate into each other. Check that this transformation leaves the massless Dirac Lagrangian

(3) invariant.