Zee A. Quantum Field Theory in a Nutshell
Подождите немного. Документ загружается.


V.6 Solitons
Breaking the shackles of Feynman diagrams
When I teach quantum field theory I like to tell the students that by the mid-1970s field
theorists were breaking the shackles of Feynman diagrams. A bit melodramatic, yes,
but by that time Feynman diagrams, because of their spectacular successes in quantum
electrodynamics, were dominating the thinking of many field theorists, perhaps to excess.
As a student I was even told that Feynman diagrams define quantum field theory, that
quantum fields were merely the “slices of venison”
1
used to derive the Feynman rules, and
should be discarded once the rules were obtained. The prevailing view was that it barely
made sense to write down ϕ(x). This view was forever shattered with the discovery of
topological solitons, as we will now discuss.
Small oscillations versus lumps
Consider once again our favorite toy model L =
1
2
(∂ϕ)
2
−V(ϕ)with the infamous double-
well potential V(ϕ)= (λ/4)(ϕ
2
− v
2
)
2
in (1 + 1)-dimensional spacetime. In chapter IV.1
we learned that of the two vacua ϕ =±v we are to pick one and study small oscillations
around it. So, pick one and write ϕ = v + χ , expand L in χ, and study the dynamics of
the χ meson with mass μ = (λv
2
)
1
2
. Physics then consists of suitably quantized waves
oscillating about the vacuum v.
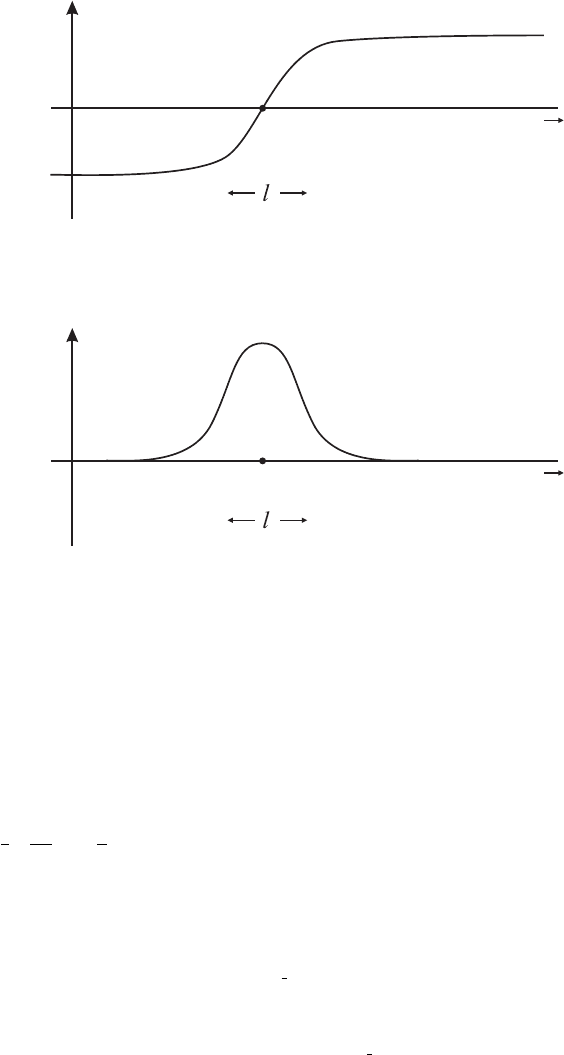
But that is not the whole story. We can also have a time independent field configuration
with ϕ(x) (in this and the next chapter x will denote only space unless it is clearly meant
to be otherwise from the context) taking on the value −v as x →−∞and +v as x →+∞,
and changing from −v to +v around some point x
0
over some length scale l as shown in
1
Gell-Mann used to speak about how pheasant meat is cooked in France between two slices of venison which
are then discarded. He forcefully advocated a program to extract and study the algebraic structure of quantum
field theories which are then discarded.
V.6. Solitons | 303
(a)
(b)
+v
−v
ϕ
x
x
0
ε
x
x
0
Figure V.6.1
figure V.6.1a. [Note that if we consider the Euclidean version of the field theory, identify
the time coordinate as the y coordinate, and think of ϕ(x, y) as the magnetization (as in
chapter V.3), then the configuration here describes a “domain wall” in a 2-dimensional
magnetic system.]
Think about the energy per unit length
ε(x) =
1
2
dϕ
dx
2
+
λ
4
(ϕ
2
− v
2
)
2
(1)
for this configuration, which I plot in figure V.6.1b. Far away from x
0
we are in one of the
two vacua and there is no energy density. Near x
0
, the two terms in ε(x) both contribute to
the energy or mass M =
dx ε(x): the “spatial variation” (in a slight abuse of terminology
often called the “kinetic energy”) term
dx
1
2
(dϕ/dx)
2
∼l(v/l)
2
∼v
2
/l, and the “potential
energy” term
dxλ(ϕ
2
− v
2
)
2
∼ lλv
4
. To minimize the total energy the spatial variation
term wants l to be large, while the potential term wants l to be small. The competition
dM/dl = 0 gives v
2
/l ∼ lλv
4
, thus fixing l ∼ (λv
2
)
−
1
2
∼ 1/μ. The mass comes out to be
∼ μv
2
∼ μ(μ
2
/λ).
We have a lump of energy spread over a region of length l of the order of the Compton
wavelength of the χ meson. By translation invariance, the center of the lump x
0
can be
anywhere. Furthermore, since the theory is Lorentz invariant, we can always boost to

304 | V. Field Theory and Collective Phenomena
send the lump moving at any velocity we like. Recalling a famous retort in the annals
of American politics (“It walks like a duck, quacks like a duck, so Mr. Senator, why don’t
you want to call it a duck?”) we have here a particle, known as a kink or a soliton, with
mass ∼ μ(μ
2
/λ) and size ∼ l. Perhaps because of the way the soliton was discovered,
many physicists think of it as a big lumbering object, but as we have seen, the size of a
soliton l ∼1/μ can be made as small as we like by increasing μ. So a soliton could look like
a point particle. We will come back to this point in chapter VI.3 when we discuss duality.
Topological stability
While the kink and the meson are the same size, for small λ the kink is much more
massive than the meson. Nevertheless, the kink cannot decay into mesons because it costs
an infinite amount of energy to undo the kink [by “lifting” ϕ(x) over the potential energy
barrier to change it from +v to −v for x from some point
>
∼
x
0
to +∞, for example]. The
kink is said to be topologically stable.
The stability is formally guaranteed by the conserved current
J
μ
=
1
2v
ε
μν
∂
ν
ϕ (2)
with the charge
Q =
+∞
−∞
dxJ
0
(x) =
1
2v
[ϕ(+∞) − ϕ(−∞)]
Mesons, which are small localized packets of oscillations in the field clearly have Q = 0,
while the kink has Q =1. Thus, the kink cannot decay into a bunch of mesons. Incidentally,
the charge density J
0
=(1/2v)(dϕ/dx) is concentrated at x
0
where ϕ changes most rapidly,
as you would expect.
Note that ∂
μ
J
μ
= 0 follows immediately from the antisymmetric symbol ε
μν
and does
not depend on the equation of motion. The current J
μ
is known as a “topological current.”
Its existence does not follow from Noether’s theorem (chapter I.10) but from topology.
Our discussion also makes clear the existence of an antikink with Q =−1 and described
by a configuration with ϕ(−∞) =+v and ϕ(+∞) =−v. The name is justified by consider-
ing the configuration pictured in figure V.6.2 containing a kink and an antikink far apart.
As the kink and the antikink move closer to each other, they clearly can annihilate into
mesons, since the configuration shown in figure V.6.2 and the vacuum configuration with
ϕ(x) =+v everywhere are separated by a finite amount of energy.
A nonperturbative phenomenon
That the mass of the kink comes out inversely proportional to the coupling λ is a clear sign
that field theorists could have done perturbation theory in λ till they were blue in the face
without ever discovering the kink. Feynman diagrams could not have told us about it.
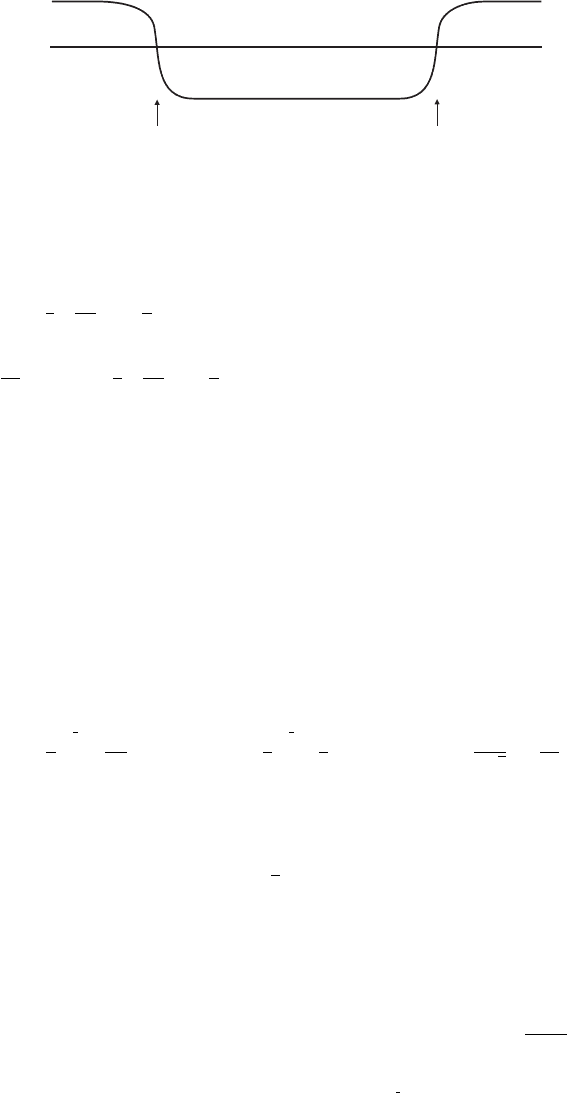
V.6. Solitons | 305
Antikink Kink
Figure V.6.2
You can calculate the mass of a kink by minimizing
M =
dx
1
2
dϕ
dx
2
+
λ
4
ϕ
2
− v
2
2
=
μ
2
λ
μ
dy
1
2
df
dy
2
+
1
4
f
2
− 1
2
where in the last step we performed the obvious scaling ϕ(x) → vf (y) and y = μx. This
scaling argument immediately showed that the mass of the kink M = a(μ
2
/λ)μ with
a a pure number: The heuristic estimate of the mass proved to be highly trustworthy.
The actual function ϕ(x) and hence a can be computed straightforwardly with standard
variational methods.
Bogomol’nyi inequality
More cleverly, observe that the energy density (1) is the sum of two squares. Using
a
2
+ b
2
≥ 2|ab| we obtain
M ≥
dx
λ
2
1
2
dϕ
dx
ϕ
2
− v
2
≥
λ
2
1
2
1
3
ϕ
3
− v
2
ϕ
2
+∞
−∞
=
4
3
√
2
μ
μ
2
λ
Q
We have the elegant result
M ≥|Q| (3)
with mass M measured in units of (4/3
√
2)μ(μ
2
/λ). This is an example of a Bogomol’nyi
inequality, which plays an important role in string theory.
Exercises
V.6.1 Show that if ϕ(x) is a solution of the equation of motion, then so is ϕ[(x −vt)/
√
1 − v
2
].
V.6.2 Discuss the solitons in the so-called sine-Gordon theory L =
1
2
(∂ϕ)
2
− g cos(βϕ). Find the topological
current. Is the Q = 2 soliton stable or not?
V.6.3 Compute the mass of the kink by the brute force method and check the result from the Bogomol’nyi
inequality.

V.7 Vortices, Monopoles, and Instantons
Vortices
The kink is merely the simplest example of a large class of topological objects in quantum
field theory.
Consider the theory of a complex scalar field in (2 + 1)-dimensional spacetime L =
∂ϕ
†
∂ϕ − λ(ϕ
†
ϕ − v
2
)
2
with the now familiar Mexican hat potential. With some minor
changes in notation, this is the theory we used to describe interacting bosons and su-
perfluids. (We choose to study the relativistic rather than the nonrelativistic version but as
you will see the issue does not enter for the questions I want to discuss here.)
Are there solitons, that is, objects like the kink, in this theory?
Given some time-independent configuration ϕ(x) let us look at its mass or energy
M =
d
2
x[∂
i
ϕ
†
∂
i
ϕ + λ(ϕ
†
ϕ − v
2
)
2
]. (1)
The integrand is a sum of two squares, each of which must give a finite contribution. In
particular, for the contribution of the second term to be finite the magnitude of ϕ must
approach v at spatial infinity.
This finite energy requirement does not fix the phase of ϕ however. Using polar coordi-
nates (r , θ) we will consider the Ansatz ϕ −→
r→∞
ve
iθ
. Writing ϕ = ϕ
1
+iϕ
2
, we see that the
vector (ϕ
1
, ϕ
2
) = v(cos θ , sin θ) points radially outward at infinity. Recall the definition of
the current J
i
=i(∂
i
ϕ
†
ϕ −ϕ
†
∂
i
ϕ) in a bosonic fluid given in chapter III.5. The flow whirls
about at spatial infinity, and thus this configuration is known as the vortex.
By explicit differentiation or dimensional analysis, we have ∂
i
ϕ ∼v(1/r) as r →∞.Now
look at the first term in M. Oops, the energy diverges logarithmically as v
2
d
2
x(1/r
2
).
Is there a way out? Not unless we change the theory.

V.7. Monopoles and Instantons | 307
Vortex into flux tubes
Suppose we gauge the theory by replacing ∂
i
ϕ by D
i
ϕ = ∂
i
ϕ − ieA
i
ϕ. Now we can achieve
finite energy by requiring that the two terms in D
i
ϕ knock each other out so that D
i
ϕ −→
r→∞
0
faster than 1/r. In other words, A
i
−→
r→∞
−(i/e)(1/|ϕ|
2
)ϕ
†
∂
i
ϕ = (1/e)∂
i
θ . Immediately, we
have
Flux ≡
d
2
xF
12
=
C
dx
i
A
i
=
2π
e
(2)
where C is an infinitely large circle at spatial infinity and we have used Stokes’ theorem.
Thus, in a gauged U(1) theory the vortex carries a magnetic flux inversely proportional to
the charge. When I say magnetic, I am presuming that A represents the electromagnetic
gauge potential. The vortex discussed here appears as a flux tube in so-called type II
superconductors. It is worth remarking that this fundamental unit of flux (2) is normally
written in the condensed matter physics literature in unnatural units as
0
=
hc
e
(3)
very pleasingly uniting three fundamental constants of Nature.
Homotopy groups
Since spatial infinity in 2 dimensional space is topologically a unit circle S
1
and since
the field configuration with |ϕ|=v also forms a circle S
1
, this boundary condition can
be characterized as a map S
1
→S
1
. Since this map cannot be smoothly deformed into the
trivial map in which S
1
is mapped onto a point in S
1
, the corresponding field configuration
is indeed topologically stable. (Think of wrapping a loop of string around a ring.)
Mathematically, maps of S
n
into a manifold M are classified by the homotopy group
n
(M), which counts the number of topologically inequivalent maps. You can look up the
homotopy groups for various manifolds in tables.
1
In particular, for n ≥ 1,
n
(S
n
) = Z,
where Z is the mathematical notation for the set of all integers. The simplest example
1
(S
1
) = Z is proved almost immediately by exhibiting the maps ϕ −→
r→∞
ve
imθ
, with m
any integer (positive or negative), using the context and notation of our discussion for
convenience. Clearly, this map wraps one circle around the other m times.
The language of homotopy groups is not just to impress people, but gives us a unifying
language to discuss topological solitons. Indeed, looking back you can now see that the
kink is a physical manifestation of
0
(S
0
) =Z
2
, where Z
2
denotes the multiplicative group
consisting of {+1, −1}(since the 0-dimensional sphere S
0
={+1, −1}consists of just two
points and is topologically equivalent to the spatial infinity in 1-dimensional space).
1
See tables 6.V and 6.VI, S. Iyanaga and Y. Kawada, eds., Encyclopedic Dictionary of Mathematics, p. 1415.
308 | V. Field Theory and Collective Phenomena
Hedgehogs and monopoles
If you absorbed all this, you are ready to move up to (3 +1)-dimensional spacetime. Spatial
infinity is now topologically S
2
. By now you realize that if the scalar field lives on the
manifold M , then we have at infinity the map of S
2
→ M. The simplest choice is thus to
take S
2
for M. Hence, we are led to scalar fields ϕ
a
(a = 1, 2, 3) transforming as a vector ϕ
under an internal symmetry group O(3) and governed by L =
1
2
∂ ϕ
.
∂ ϕ −V(ϕ
.
ϕ). (There
should be no confusion in using the arrow to indicate a vector in the internal symmetry
group.)
Let us choose V =λ( ϕ
2
− v
2
)
2
. The story unfolds much as the story of the vortex. The
requirement that the mass of a time independent configuration
M =
d
3
x[
1
2
(∂ ϕ)
2
+ λ( ϕ
2
− v
2
)
2
] (4)
be finite forces |ϕ|=v at spatial infinity so that ϕ(r =∞) indeed lives on S
2
.
The identity map S
2
→ S
2
indicates that we should consider a configuration such that
ϕ
a
−→
r→∞
v
x
a
r
(5)
This equation looks a bit strange at first sight since it mixes the index of the internal
symmetry group with the index of the spatial coordinates (but in fact we have already
encountered this phenomenon in the vortex). At spatial infinity, the field ϕ is pointing
radially outward, so this configuration is known picturesquely as a hedgehog. Draw a
picture if you don’t get it!
As in the vortex story, the requirement that the first term in (4) be finite forces us to
introduce an O(3) gauge potential A
b
μ
so that we can replace the ordinary derivative ∂
i
ϕ
a
by the covariant derivative D
i
ϕ
a
=∂
i
ϕ
a
+eε
abc
A
b
i
ϕ
c
. We can then arrange D
i
ϕ
a
to vanish
at infinity. Simple arithmetic shows that with (5) the gauge potential has to go as
A
b
i
−→
r→∞
1
e
ε
bij
x
j
r
2
(6)
Imagine yourself in a lab at spatial infinity. Inside a small enough lab, the ϕ field at
different points are all pointing in approximately the same direction. The gauge group
O(3) is broken down to O(2) U(1). The experimentalists in this lab observe a massless
gauge field associated with the U(1), which they might as well call the electromagnetic
field (“quacks like a duck”). Indeed, the gauge invariant tensor field
F
μν
≡
F
a
μν
ϕ
a
|ϕ|
−
ε
abc
ϕ
a
(D
μ
ϕ)
b
(D
ν
ϕ)
c
e|ϕ|
3
(7)
can be identified as the electromagnetic field (see exercise V.7.5).
There is no electric field since the configuration is time independent and A
b
0
= 0. We
can only have a magnetic field
B which you can immediately calculate since you know A
b
i
,
but by symmetry we already see that
B can point only in the radial direction.
This is the fabled magnetic monopole first postulated by Dirac!

V.7. Monopoles and Instantons | 309
The presence of magnetic monopoles in spontaneously broken gauge theory was dis-
covered by ’t Hooft and Polyakov. If you calculate the total magnetic flux coming out of the
monopole
d
S
.
B, where as usual d
S denotes a small surface element at infinity pointing
radially outward, you will find that it is quantized in suitable units, exactly as Dirac had
stated, as it must (recall chapter IV.4).
We can once again write a Bogomol’nyi inequality for the mass of the monopole
M =
d
3
x
1
4
(
F
ij
)
2
+
1
2
(D
i
ϕ)
2
+ V(ϕ)
(8)
[
F
ij
transforms as a vector under O(3); recall (IV.5.17).] Observe that
1
4
(
F
ij
)
2
+
1
2
(D
i
ϕ)
2
=
1
4
(
F
ij
± ε
ij k
D
k
ϕ)
2
∓
1
2
ε
ij k
F
ij
.
D
k
ϕ
Thus
M ≥
d
3
x
∓
1
2
ε
ij k
F
ij
.
D
k
ϕ + V(ϕ)
(9)
We next note that
d
3
x
1
2
ε
ij k
F
ij
.
D
k
ϕ =
d
3
x
1
2
ε
ij k
∂
k
(
F
ij
.
ϕ) = v
d
S
.
B = 4πvg
has an elegant interpretation in terms of the magnetic charge g of the monopole. Further-
more, if we can throw away V(ϕ) while keeping |ϕ|−→
r→∞
v, then the inequality M ≥4πv|g|
is saturated by
F
ij
=±ε
ij k
D
k
ϕ. The solutions of this equation are known as Bogomol’nyi-
Prasad-Sommerfeld or BPS states.
It is not difficult to construct an electrically charged magnetic monopole, known as a
dyon. We simply take A
b
0
= (x
b
/r)f (r) with some suitable function f(r).
One nice feature of the topological monopole is that its mass comes out to be ∼M
W
/α ∼
137M
W
(exercise V.7.11), where M
W
denotes the mass of the intermediate vector boson of
the weak interaction. We are anticipating chapter VII.2 a bit in that the gauge boson that
becomes massive by the Anderson-Higgs mechanism of chapter IV.6 may be identified
with the intermediate vector boson. This explains naturally why the monopole has not yet
been discovered.
Instanton
Consider a nonabelian gauge theory, and rotate the path integral to 4-dimensional Eu-
clidean space. We might wish to evaluate Z =
DAe
−S(A)
in the steepest descent approx-
imation, in which case we would have to find the extrema of
S(A) =
d
4
x
1
2g
2
tr F
μν
F
μν
with finite action. This implies that at infinity |x|=∞, F
μν
must vanish faster than 1/|x|
2
,
and so the gauge potential A
μ
must be a pure gauge: A = gdg
†
for g an element of the
gauge group [see (IV.5.6)]. Configurations for which this is true are known as instantons.

310 | V. Field Theory and Collective Phenomena
We see that the instanton is yet one more link in the “great chain of being”: kink-vortex-
monopole-instanton.
Choose the gauge group SU(2) to be definite. In the parametrization g = x
4
+ i x
.
σ
we have by definition g
†
g = 1 and det g = 1, thus implying x
2
4
+x
2
= 1. We learn that
the group manifold of SU(2) is S
3
. Thus, in an instanton, the gauge potential at infinity
A −→
|x|→∞
gdg
†
+O(1/|x|
2
) defines a map S
3
→S
3
. Sound familiar? Indeed, you’ve already
seen S
0
→ S
0
, S
1
→ S
1
, S
2
→ S
2
playing a role in field theory.
Recall from chapter IV.5 that tr F
2
= d tr(AdA +
2
3
A
3
). Thus
tr F
2
=
S
3
tr(AdA +
2
3
A
3
) =
S
3
tr(AF −
1
3
A
3
) =−
1
3
S
3
tr(gdg
†
)
3
(10)
where we used the fact that F vanishes at infinity. This shows explicitly that
trF
2
depends only on the homotopy of the map S
3
→ S
3
defined by g and is thus a topological
quantity. Incidentally,
S
3
tr(gdg
†
)
3
is known to mathematicians as the Pontryagin index
(see exercise V.7.12).
I mentioned in chapter IV.7 that the chiral anomaly is not affected by higher-order
quantum fluctuations. You are now in position to give an elegant topological proof of this
fact (exercise V.7.13).
Kosterlitz-Thouless transition
We were a bit hasty in dismissing the vortex in the nongauged theory L =∂ϕ
†
∂ϕ −λ(ϕ
†
ϕ −
v
2
)
2
in (2 + 1)-dimensional spacetime. Around a vortex ϕ ∼ ve
iθ
and so it is true, as we
have noted, that the energy of a single vortex diverges logarithmically. But what about a
vortex paired with an antivortex?
Picture a vortex and an antivortex separated by a distance R large compared to the
distance scales in the theory. Around an antivortex ϕ ∼ ve
−iθ
. The field ϕ winds around
the vortex one way and around the antivortex the other way. Convince yourself by drawing
a picture that at spatial infinity ϕ does not wind at all: It just goes to a fixed value. The
winding one way cancels the winding the other way.
Thus, a configuration consisting of a vortex-antivortex pair does not cost infinite energy.
But it does cost a finite amount of energy: In the region between the vortex and the
antivortex ϕ is winding around, in fact roughly twice as fast (as you can see by drawing a
picture). A rough estimate of the energy is thus v
2
d
2
x(1/r
2
) ∼ v
2
log(R/a), where we
integrated over a region of size R, the relevant physical scale in the problem. (To make
sense of the problem we divide R by the size a of the vortex.) The vortex and the antivortex
attract each other with a logarithmic potential. In other words, the configuration cannot
be static: The vortex and the antivortex want to get together and annihilate each other in
a fiery embrace and release that finite amount of energy v
2
log(R/a). (Hence the term
antivortex.)
All of this is at zero temperature, but in condensed matter physics we are interested in
the free energy F = E − TS (with S the entropy) at some temperature T rather than the
V.7. Monopoles and Instantons | 311
energy E. Appreciating this elementary point, Kosterlitz and Thouless discovered a phase
transition as the temperature is raised. Consider a gas of vortices and antivortices at some
nonzero temperature. Because of thermal agitation, the vortices and antivortices moving
around may or may not find each other to annihilate. How high do we have to crank up
the temperature for this to happen?
Let us do a heuristic estimate. Consider a single vortex. Herr Boltzmann tells us that the
entropy is the logarithm of the “number” of ways in which we can put the vortex inside
a box of size L (which we will let tend to infinity). Thus, S ∼ log (L/a). The entropy S is
to battle the energy E ∼ v
2
log(L/a). We see that the free energy F ∼ (v
2
− T)log(L/a)
goes to infinity if T
<
∼
v
2
, which we identify as essentially the critical temperature T
c
.
A single vortex cannot exist below T
c
. Vortices and antivortices are tightly bound below
T
c
but are liberated above T
c
.
Black hole
The discovery in the 1970s of these topological objects that cannot be seen in perturbation
theory came as a shock to the generation of physicists raised on Feynman diagrams and
canonical quantization. People (including yours truly) were taught that the field operator
ϕ(x) is a highly singular quantum operator and has no physical meaning as such, and
that quantum field theory is defined perturbatively by Feynman diagrams. Even quite
eminent physicists asked in puzzlement what a statement such as ϕ −→
r→∞
ve
iθ
would mean.
Learned discussions that in hindsight are totally irrelevant ensued. As I said in introducing
chapter V.6, I like to refer to this historical process as “field theorists breaking the shackles
of Feynman diagrams.”
It is worth mentioning one argument physicists at that time used to convince themselves
that solitons do exist. After all, the Schwarzschild black hole, defined by the metric g
μν
(x)
(see chapter I.11), had been known since 1916. Just what are the components of the metric
g
μν
(x)? They are fields in exactly the same way that our scalar field ϕ(x) and our gauge
potential A
μ
(x) are fields, and in a quantum theory of gravity g
μν
would have to be replaced
by a quantum operator just like ϕ and A
μ
. So the objects discovered in the 1970s are
conceptually no different from the black hole known in the 1910s. But in the early 1970s
most particle theorists were not particularly aware of quantum gravity.
Exercises
V.7.1 Explain the relation between the mathematical statement
0
(S
0
) =Z
2
and the physical result that there
are no kinks with |Q|≥2.
V.7.2 In the vortex, study the length scales characterizing the variation of the fields ϕ and A. Estimate the mass
of the vortex.
