Zee A. Quantum Field Theory in a Nutshell
Подождите немного. Документ загружается.


332 | VI. Field Theory and Condensed Matter
which upon absorbing θ into A by a gauge transformation we recognize as the Meissner
Lagrangian. For later convenience we also introduce the alternative form
L =−
1
2v
2
ξ
2
μ
+ ξ
μ
(∂
μ
θ −qA
μ
) (3)
We recover (2) upon eliminating the auxiliary field ξ
μ
(see appendix A and chapter III.5).
In chapter V.7 we learned that the excitation spectrum includes vortices and anti-
vortices, located where |ϕ| vanishes. If, around the zero of |ϕ|, θ changes by 2π , we have
a vortex. Around an antivortex, θ =−2π. Recall that around a vortex sitting at rest, the
electromagnetic gauge potential has to go as
qA
i
→ ∂
i
θ (4)
at spatial infinity in order for the energy of the vortex to be finite, as we can see from (2).
The magnetic flux
d
2
xε
ij
∂
i
A
j
=
d x
.
A =
θ
vortex
q
=
2π
q
(5)
is quantized in units of 2π/q.
Let us pause to think physically for a minute. On a distance scale large compared to the
size of the vortex, vortices and antivortices appear as points. As discussed in chapter V.7,
the interaction energy of a vortex and an antivortex separated by a distance R is given
by simply plugging into (2). Ignoring the probe field A
μ
, which we can take to be as
weak as possible, we obtain ∼
R
a
dr r(∇θ)
2
∼ log(R/a) where a is some short distance
cutoff. But recall that the Coulomb interaction in 2-dimensional space is logarithmic since
by dimensional analysis
d
2
k(e
i
k
.
x
/k
2
) ∼ log (|x|/a) (with a
−1
some ultraviolet cutoff).
Thus, a gas of vortices and antivortices appears as a gas of point “charges” with a Coulomb
interaction between them.
Vortex as charge in a dual theory
Duality is often made out by some theorists to be a branch of higher mathematics but
in fact it derives from an entirely physical idea. In view of the last paragraph, can we not
rewrite the theory so that vortices appear as point “charges” of some as yet unknown gauge
field? In other words, we want a dual theory in which the fundamental field creates and
annihilates vortices rather than ϕ quanta. We will explain the word “dual” in due time.
Remarkably, the rewriting can be accomplished in just a few simple steps. Proceeding
physically and heuristically, we picture the phase field θ as smoothly fluctuating, except
that here and there it winds around 2π . Write ∂
μ
θ =∂
μ
θ
smooth
+ ∂
μ
θ
vortex
. Plugging into
(3) we write
L =−
1
2v
2
ξ
2
μ
+ ξ
μ
(∂
μ
θ
smooth
+ ∂
μ
θ
vortex
− qA
μ
) (6)
Integrate over θ
smooth
and obtain the constraint ∂
μ
ξ
μ
= 0, which can be solved by writing
ξ
μ
= ε
μνλ
∂
ν
a
λ
(7)

VI.3. Duality | 333
a trick we used earlier in chapter VI.2. As in that chapter, a gauge potential comes looking
for us, since the change a
λ
→ a
λ
+ ∂
λ
does not change ξ
μ
. Plugging into (6), we find
L =−
1
4v
2
f
2
μν
+ ε
μνλ
∂
ν
a
λ
(∂
μ
θ
vortex
− qA
μ
) (8)
where f
μν
= ∂
μ
a
ν
− ∂
ν
a
μ
.
Our treatment is heuristic because we ignore the fact that |ϕ| vanishes at the vortices.
Physically, we think of the vortices as almost pointlike so that |ϕ|=v “essentially” every-
where. As mentioned in chapter V.6, by appropriate choice of parameters we can make
solitons, vortices, and so on as small as we like. In other words, we neglect the coupling
between θ
vortex
and |ϕ|. A rigorous treatment would require a proper short distance cutoff
by putting the system on a lattice.
2
But as long as we capture the essential physics, as we
assuredly will, we will ignore such niceties.
Note for later use that the electromagnetic current J
μ
, defined as the coefficient of −A
μ
in (8), is determined in terms of the gauge potential a
λ
to be
J
μ
= qε
μνλ
∂
ν
a
λ
(9)
Let us integrate the term ε
μνλ
∂
ν
a
λ
∂
μ
θ
vortex
in (8) by parts to obtain a
λ
ε
λμν
∂
μ
∂
ν
θ
vortex
.
According to Newton and Leibniz, ∂
μ
commutes with ∂
ν
, and so apparently we get zero.
But ∂
μ
and ∂
ν
commute only when acting on a globally defined function, and, heavens to
Betsy, θ
vortex
is not globally defined since it changes by 2π when we go around a vortex.
In particular, consider a vortex at rest and look at the quantity a
0
couples to in (8) namely
ε
ij
∂
i
∂
j
θ
vortex
=
∇×(
∇θ
vortex
) in the notation of elementary physics. Integrating this over
a region containing the vortex gives
d
2
x
∇×(
∇θ
vortex
) =
d x
.
∇θ
vortex
= 2π . Thus, we
recognize (1/2π)ε
ij
∂
i
∂
j
θ
vortex
as the density of vortices, the time component of some vortex
current j
λ
vortex
. By Lorentz invariance, j
λ
vortex
= (1/2π)ε
λμν
∂
μ
∂
ν
θ
vortex
.
Thus, we can now write (8) as
L =−
1
4v
2
f
2
μν
+ (2π)a
μ
j
μ
vortex
− A
μ
(qε
μνλ
∂
ν
a
λ
) (10)
Lo and behold, we have accomplished what we set out to do. We have rewritten the theory
so that the vortex appears as an “electric charge” for the gauge potential a
μ
. Sometimes
this is called a dual theory, but strictly speaking, it is more accurate to refer to it as the dual
representation of the original theory (1).
Let us introduce a complex scalar field , which we will refer to as the vortex field,
to create and annihilate the vortices and antivortices. In other words, we “elaborate” the
description in (10) to
L =−
1
4v
2
f
2
μν
+
1
2
|(∂
μ
− i(2π)a
μ
)|
2
− W () − A
μ
(qε
μνλ
∂
ν
a
λ
) (11)
2
For example, M. P. A. Fisher, “Mott Insulators, Spin Liquids, and Quantum Disordered Superconductivity,”
cond-mat/9806164, appendix A.
334 | VI. Field Theory and Condensed Matter
The potential W () contains terms such as λ(
†
)
2
describing the short distance inter-
action of two vortices (or a vortex and an antivortex.) In principle, if we master all the short
distance physics contained in the original theory (1) then these terms are all determined
by the original theory.
Vortex of a vortex
Now we come to the most fascinating aspect of the duality representation and the reason
why the word “dual” is used in the first place. The vortex field is a complex scalar field,
just like the field ϕ we started with. Thus we can perfectly well form a vortex out of ,
namely a place where vanishes and around which the phase of goes through 2π .
Amusingly, we are forming a vortex of a vortex, so to speak.
So, what is a vortex of a vortex?
The duality theorem states that the vortex of a vortex is nothing but the original charge,
described by the field ϕ we started out with! Hence the word duality.
The proof is remarkably simple. The vortex in the theory (11) carries “magnetic flux.”
Referring to (11) we see that 2πa
i
→∂
i
θ at spatial infinity. By exactly the same manipulation
as in (5), we have
2π
d
2
xε
ij
∂
i
a
j
= 2π
d x
.
a = 2π (12)
Note that I put quotation marks around the term “magnetic flux” since as is evident I am
talking about the flux associated with the gauge potential a
μ
and not the flux associated
with the electromagnetic potential A
μ
. But remember that from (9) the electromagnetic
current J
μ
= qε
μνλ
∂
ν
a
λ
and in particular J
0
= qε
ij
∂
i
a
j
. Hence, the electric charge (note
no quotation marks) of this vortex of a vortex is equal to
d
2
xJ
0
=q, precisely the charge
of the original complex scalar field ϕ. This proves the assertion.
Here we have studied vortices, but the same sort of duality also applies to monopoles.
As I remarked in chapter IV.4, duality allows us a glimpse into field theories in the strongly
coupled regime. We learned in chapter V.7 that certain spontaneously broken nonabelian
gauge theories in (3 + 1)-dimensional spacetime contains magnetic monopoles. We can
write a dual theory in terms of the monopole field out of which we can construct mono-
poles. The monopole of a monopole turns out be none other than the charged fields of the
original gauge theory. This duality was first conjectured many years ago by Olive and Mon-
tonen and later shown to be realized in certain supersymmetric gauge theories by Seiberg
and Witten. The understanding of this duality was a “hot” topic a few years ago as it led
to deep new insight about how certain string theories are dual to each other.
3
In contrast,
according to one of my distinguished condensed matter colleagues, the important notion
of duality is still underappreciated in the condensed matter physics community.
3
For example, D. I. Olive and P. C. West, eds., Duality and Supersymmetric Theories.
VI.3. Duality | 335
Meissner begets Maxwell and so on
We will close by elaborating slightly on duality in (2 + 1)-dimensional spacetime and how
it might be relevant to the physics of 2-dimensional materials. Consider a Lagrangian L(a)
quadratic in a vector field a
μ
. Couple an external electromagnetic gauge potential A
μ
to
the conserved current ε
μνλ
∂
ν
a
λ
:
L = L(a) + A
μ
(ε
μνλ
∂
ν
a
λ
) (13)
Let us ask: For various choices of L(a), if we integrate out a what is the effective
Lagrangian L(A) describing the dynamics of A?
If you have gotten this far in the book, you can easily do the integration. The central
identity of quantum field theory again! Given
L(a) ∼ aKa (14)
we have
L(A) ∼ (ε∂A)
1
K
(ε∂A) ∼ A(ε∂
1
K
ε∂)A (15)
We have three choices for L(a) to which I attach various illustrious names:
L(a) ∼ a
2
Meissner
L(a) ∼ aε∂a Chern-Simons (16)
L(a) ∼ f
2
∼ a∂
2
a Maxwell
Since we are after conceptual understanding, I won’t bother to keep track of indices and
irrelevant overall constants. (You can fill them in as an exercise.) For example, given
L(a) = f
μν
f
μν
with f
μν
= ∂
μ
a
ν
− ∂
ν
a
μ
we can write L(a) ∼ a∂
2
a and so K =∂
2
. Thus,
the effective dynamics of the external electromagnetic gauge potential is given by (15) as
L(A) ∼ A[ε∂(1/∂
2
)ε∂]A ∼ A
2
, the Meissner Lagrangian! In this “quick and dirty” way of
making a living, we simply set εε ∼ 1 and cancel factors of ∂ in the numerator against
those in the denominator. Proceeding in this way, we construct the following table:
Dynamics of a K Effective Lagrangian
L(A) ∼ A[ε∂(1/K)ε∂]A
Dynamics of the
external probe A
Meissner a
2
1 A(ε∂ε∂)A ∼ A∂
2
A Maxwell F
2
Chern-Simons aε∂a
ε∂
A(ε∂
1
ε∂
ε∂)A ∼ Aε∂A
Chern-Simons
Aε∂A
Maxwell f
2
∼ a∂
2
a ∂
2
A(ε∂
1
∂
2
ε∂)A ∼ AA Meissner A
2
(17)

336 | VI. Field Theory and Condensed Matter
Meissner begets Maxwell, Chern-Simons begets Chern-Simons, and Maxwell begets
Meissner. I find this beautiful and fundamental result, which represents a form of duality,
very striking. Chern-Simons is self-dual: It begets itself.
Going nonrelativistic
It is instructive to compare the nonrelativistic treatment of duality.
4
Go back to the super-
fluid Lagrangian of chapter V.1:
L = iϕ
†
∂
0
ϕ −
1
2m
∂
i
ϕ
†
∂
i
ϕ − g
2
(ϕ
†
ϕ −¯ρ)
2
(18)
As before, substitute ϕ ≡
√
ρe
iθ
to obtain
L =−ρ∂
0
θ −
ρ
2m
(∂
i
θ)
2
− g
2
(ρ −¯ρ)
2
+
...
(19)
which we rewrite as
L =−ξ
μ
∂
μ
θ +
m
2ρ
ξ
2
i
− g
2
(ρ −¯ρ)
2
+
...
(20)
In (19) we have dropped a term ∼ (∂
i
ρ
1/2
)
2
. In (20) we have defined ξ
0
≡ ρ. Integrating
out ξ
i
in (20) we recover (19).
All proceeds as before. Writing θ = θ
smooth
+ θ
vortex
and integrating out θ
smooth
,we
obtain the constraint ∂
μ
ξ
μ
= 0, solved by writing ξ
μ
=
μνλ
∂
ν
ˆa
λ
. The hat on ˆa
λ
is for later
convenience. Note that the density
ξ
0
≡ ρ =
ij
∂
i
ˆa
j
≡
ˆ
f (21)
is the “magnetic” field strength while
ξ
i
=
ij
(∂
0
ˆa
j
− ∂
j
ˆa
0
) ≡
ij
ˆ
f
0j
(22)
is the “electric” field strength.
Putting all of this into (20) we have
L =
m
2ρ
ˆ
f
2
0i
− g
2
(
ˆ
f −¯ρ)
2
− 2π ˆa
μ
j
μ
vortex
+
...
(23)
To “subtract out” the background “magnetic” field ¯ρ, an obviously sensible move is to write
ˆa
μ
=¯a
μ
+ a
μ
(24)
where we define the background gauge potential by ¯a
0
= 0, ∂
0
¯a
j
= 0 (no background
“electric” field) and
ij
∂
i
¯a
j
=¯ρ (25)
4
The treatment given here follows essentially that given by M. P. A. Fisher and D. H. Lee.

VI.3. Duality | 337
The Lagrangian (23) then takes on the cleaner form
L =
m
2 ¯ρ
f
2
0i
− g
2
f
2
− 2πa
μ
j
μ
vortex
− 2π ¯a
i
j
i
vortex
+
...
(26)
We have expanded ρ ∼¯ρ in the first term. As in (10) the first two terms form the Maxwell
Lagrangian, and the ratio of their coefficients determines the speed of propagation
c =
2g
2
¯ρ
m
1/2
(27)
In suitable units in which c = 1, we have
L =−
m
4 ¯ρ
f
μν
f
μν
− 2πa
μ
j
μ
vortex
− 2π ¯a
i
j
i
vortex
+
...
(28)
Compare this with (10).
The one thing we missed with our relativistic treatment is the last term in (28), for
the simple reason that we didn’t put in a background. Recall that the term like A
i
J
i
in
ordinary electromagnetism means that a moving particle associated with the current J
i
sees a magnetic field
∇×
A. Thus, a moving vortex will see a “magnetic field”
ij
∂
i
( ¯a + a)
j
=¯ρ +
ij
∂
i
a
j
(29)
equal to the sum of ¯ρ, the density of the original bosons, and a fluctuating field.
In the Coulomb gauge ∂
i
a
i
=0 we have (f
0i
)
2
=(∂
0
a
i
)
2
+(∂
i
a
0
)
2
, where the cross term
(∂
0
a
i
)(∂
i
a
0
) effectively vanishes upon integration by parts. Integrating out the Coulomb
field a
0
, we obtain
L =−
¯ρ
2m
(2π)
2
d
2
xd
2
y
j
0
(x) log
|x −y|
a
j
0
(y)
+
m
2 ¯ρ
(∂
0
a
i
)
2
− g
2
f
2
+ 2π(a
i
+¯a
i
)j
vortex
i
(30)
The vortices repel each other by a logarithmic interaction
d
2
k(e
i
k
.
x
/k
2
) ∼ log(|x|/a) as
we have known all along.
A self-dual theory
Interestingly, the spatial part f
2
of the Maxwell Lagrangian comes from the short ranged
repulsion between the original bosons.
If we had taken the bosons to interact by an arbitrary potential V(x) we would have,
instead of the last term in (20),
d
2
xd
2
y
[
ρ(x) −¯ρ
]
V(x − y)
[
ρ(y) −¯ρ
]
(31)
It is easy to see that all the steps go through essentially as before, but now the second term
in (26) becomes
d
2
xd
2
yf (x)V (x − y)f (y) (32)

338 | VI. Field Theory and Condensed Matter
Thus, the gauge field propagates according to the dispersion relation
ω
2
= (2 ¯ρ/m)V (k)
k
2
(33)
where V(k)is the Fourier transformation of V(x). In the special case V(x)= g
2
δ
(2)
(x) we
recover the linear dispersion given in (27). Indeed, we have a linear dispersion ω ∝|
k| as
long as V(x)is sufficiently short ranged for V(
k = 0) to be finite.
An interesting case is when V(x) is logarithmic. Then V(k) goes as 1/k
2
and so ω ∼
constant: The gauge field a
i
becomes massive and drops out. The low energy effective
theory consists of a bunch of vortices with a logarithmic interaction between them. Thus,
a theory of bosons with a logarithmic repulsion between them is self dual in the low energy
limit.
The dance of vortices and antivortices
Having gone through this nonrelativistic discussion of duality, let us reward ourselves by
deriving the motion of vortices in a fluid. Let the bulk of the fluid be at rest. According to (28)
the vortex behaves like a charged particle in a background magnetic field
¯
b proportional to
the mean density of the fluid ¯ρ. Thus, the force acting on a vortex is the usual Lorentz force
v ×
B, and the equation of motion of the vortex in the presence of a force F is then just
¯ρ
ij
˙x
j
= F
i
(34)
This is the well-known result that a vortex, when pushed, moves in a direction perpendic-
ular to the force.
Consider two vortices. According to (30) they repel each other by a logarithmic inter-
action. They move perpendicular to the force. Thus, they end up circling each other. In
contrast, consider a vortex and an antivortex, which attract each other. As a result of this
attraction, they both move in the same direction, perpendicular to the straight line joining
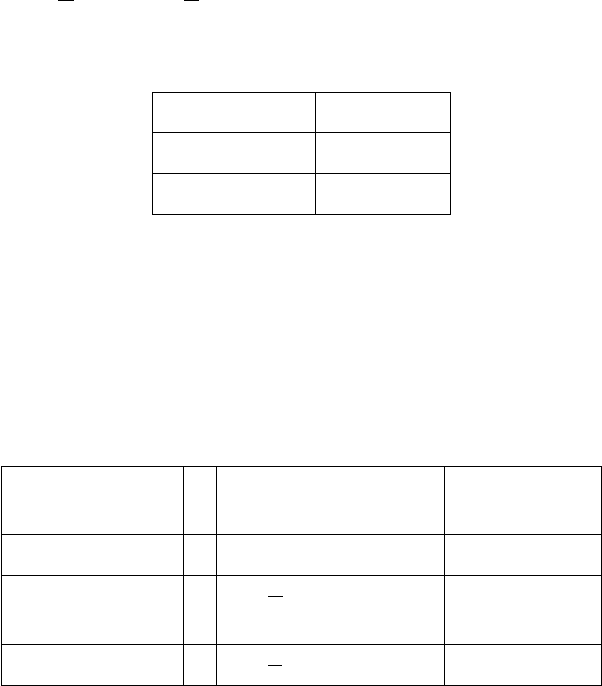
them (see fig. VI.3.1). The vortex and antivortex move along in step, maintaining the dis-
tance between them. This in fact accounts for the famous motion of a smoke ring. If we
cut a smoke ring through its center and perpendicular to the plane it lies in, we have just
+
+
_
(a)
(b)
+
Figure VI.3.1
VI.3. Duality | 339
a vortex with an antivortex for each section. Thus, the entire smoke ring moves along in a
direction perpendicular to the plane it lies in.
All of this can be understood by elementary physics, as it should be. The key observation
is simply that vortices and antivortices produce circular flows in the fluid around them, say
clockwise for vortices and anticlockwise for antivortices. Another basic observation is that
if there is a local flow in the fluid, then any object, be it a vortex or an antivortex, caught in
it would just flow along in the same direction as the local flow. This is a consequence of
Galilean invariance. By drawing a simple picture you can see that this produces the same
pattern of motion as discussed above.

VI.4 The σ Models as Effective Field Theories
The Lagrangian as a mnemonic
Our beloved quantum field theory has had two near death experiences. The first started
around the mid-1930s when physical quantities came out infinite. But it roared back to
life in the late 1940s and early 1950s, thanks to the work of the generation that included
Feynman, Schwinger, Dyson, and others. The second occurred toward the late 1950s. As
we have already discussed, quantum field theory seemed totally incapable of addressing
the strong interaction: The coupling was far too strong for perturbation theory to be of any
use. Many physicists—known collectively as the S-matrix school—felt that field theory
was irrelevant for studying the strong interaction and advocated a program of trying to
derive results from general principles without using field theory. For example, in deriving
the Goldberger-Treiman relation, we could have foregone any mention of field theory and
Feynman diagrams.
Eventually, in a reaction against this trend, people realized that if some results could be
obtained from general considerations such as notions of spontaneous symmetry breaking
and so forth, any Lagrangian incorporating these general properties had to produce the
same results. At the very least, the Lagrangian provides a mnemonic for any physical result
derived without using quantum field theory. Thus was born the notion of long distance
or low energy effective field theory, which would prove enormously useful in both particle
and condensed matter physics (as we have already seen and as we will discuss further in
chapter VIII.3).
The strong interaction at low energies
One of the earliest examples is the σ model of Gell-Mann and L
´
evy, which describes the
interaction of nucleons and pions. We now know that the strong interaction has to be
described in terms of quarks and gluons. Nevertheless, at long distances, the degrees of

VI.4. σ Models | 341
freedom are the two nucleons and the three pions. The proton and the neutron transform as
a spinor ψ ≡
p
n
under the SU(2) of isospin. Consider the kinetic energy term
¯
ψiγ∂ψ =
¯
ψ
L
iγ∂ψ
L
+
¯
ψ
R
iγ∂ψ
R
. We note that this term has the larger symmetry SU(2)
L
×SU(2)
R
,
with the left handed field ψ
L
and the right handed field ψ
R
transforming as a doublet
under SU(2)
L
and SU(2)
R
, respectively. [The SU(2) of isospin is the diagonal subgroup
of SU(2)
L
× SU(2)
R
.] We can write ψ
L
∼ (
1
2
,0) and ψ
R
∼ (0,
1
2
).
Now we see a problem immediately: The mass term m
¯
ψψ = m(
¯
ψ
L
ψ
R
+ h.c.) is not
allowed since
¯
ψ
L
ψ
R
∼ (
1
2
,
1
2
), a 4-dimensional representation of SU(2)
L
× SU(2)
R
,a
group locally isomorphic to SO(4).
At this point, lesser physicists would have said, what is the problem, we knew all along
that the strong interaction is invariant only under the SU(2) of isospin, which we will
write as SU(2)
I
. Under SU(2)
I
the bilinears constructed out of
¯
ψ
L
and ψ
R
transform as
1
2
×
1
2
=0 + 1, the singlet being
¯
ψψ and the triplet
¯
ψiγ
5
τ
a
ψ. With only SU(2)
I
symmetry,
we can certainly include the mass term
¯
ψψ.
To say it somewhat differently, to fully couple to the four bilinears we can construct out
of
¯
ψ
L
and ψ
R
, namely
¯
ψψ and
¯
ψiγ
5
τ
a
ψ , we need four meson fields transforming as the
vector representation under SO(4). But only the three pion fields are known. It seems
clear that we only have SU(2)
I
symmetry.
Nevertheless, Gell-Mann and L
´
evy boldly insisted on the larger symmetry SU(2)
L
×
SU(2)
R
SO(4) and simply postulated an additional meson field, which they called σ ,
so that (σ , π) form the 4-dimensional representation. I leave it to you to verify that
¯
ψ
L
(σ + i τ
.
π)ψ
R
+ h.c. =
¯
ψ(σ + i τ
.
πγ
5
)ψ is invariant. Hence, we can write down the
invariant Lagrangian
L =
¯
ψ[iγ∂ + g(σ + i τ
.
πγ
5
)]ψ + L(σ , π) (1)
where the part not involving the nucleons reads
L(σ , π) =
1
2
(∂σ )
2
+ (∂ π)
2
+
μ
2
2
(σ
2
+π
2
) −
λ
4
(σ
2
+π
2
)
2
(2)
This is known as the linear σ model.
The σ model would have struck most physicists as rather strange at the time it was
introduced: The nucleon does not have a mass and there is an extra meson field. Aha, but
you would recognize (2) as precisely the Lagrangian (IV.1.2) (for N =4) that we studied,
which exhibits spontaneous symmetry breaking. The four scalar fields (ϕ
4
, ϕ
1
, ϕ
2
, ϕ
3
)
in (IV.1.2) correspond to (σ , π). With no loss of generality, we can choose the vacuum
expectation value of ϕ to point in the 4th direction, namely the vacuum in which 0|σ |0=
μ
2
/λ ≡ v and 0|π |0=0. Expanding σ = v + σ
we see immediately that the nucleon
has a mass M = gv. You should not be surprised that the pion comes out massless. The
meson associated with the field σ
, which we will call the σ meson, has no reason to be
massless and indeed is not.
Can the all-important parameter v be related to a measurable quantity? Indeed. From
chapter I.10 you will recall that the axial current is given by Noether’s theorem as
J
a
μ5
=
¯
ψγ
μ
γ
5
(τ
a
/2)ψ + π
a
∂
μ
σ − σ∂
μ
π
a
. After σ acquires a vacuum expectation value,
