Zee A. Quantum Field Theory in a Nutshell
Подождите немного. Документ загружается.

342 | VI. Field Theory and Condensed Matter
J
a
μ5
contains a term −v∂
μ
π
a
. This term implies that the matrix element 0|J
a
μ5
|π
b
=ivk
μ
,
where k denotes the momentum of the pion, and thus v is proportional to the f defined in
chapter IV.2. Indeed, we recognize the mass relation M =gv as precisely the Goldberger-
Treiman relation (IV.2.7) with F(0) = 1 (see exercise VI.4.4).
The nonlinear σ model
It was eventually realized that the main purpose in life of the potential in L(σ , π) is to
force the vacuum expectation values of the fields to be what they are, so the potential can
be replaced by a constraint σ
2
+π
2
=v
2
. A more physical way of thinking about this point
is by realizing that the σ meson, if it exists at all, must be very broad since it can decay
via the strong interaction into two pions. We might as well force it out of the low energy
spectrum by making its mass large. By now, you have learned from chapters IV.1 and V.1
that the mass of the σ meson, namely
√
2μ, can be taken to infinity while keeping v fixed
by letting μ
2
and λ tend to infinity, keeping their ratio fixed.
We will now focus on L(σ , π). Instead of thinking abut L(σ , π) =
1
2
[(∂σ )
2
+ (∂ π)
2
]
with the constraint σ
2
+π
2
=v
2
, we can simply solve the constraint and plug the solution
σ =
√
v
2
−π
2
into the Lagrangian, thus obtaining what is known as the nonlinear σ model:
L =
1
2
(∂ π)
2
+
( π
.
∂ π)
2
f
2
−π
2
=
1
2
(∂ π)
2
+
1
2f
2
( π
.
∂ π)
2
+
...
(3)
Note that L can be written in the form L = (∂π
a
)G
ab
( π)(∂π
b
); some people like to think of
G
ab
as a “metric” in field space. [Incidentally, recall that way back in chapter I.3 we restricted
ourselves to the simplest possible kinetic energy term
1
2
(∂ϕ)
2
, rejecting possibilities such
as U (ϕ)(∂ϕ)
2
. But recall also that in chapter IV.3 we noted that such a term would arise by
quantum fluctuations.]
In accordance with the philosophy that introduced this chapter, any Lagrangian that
captures the correct symmetry properties should describe the same low energy physics.
1
This means that anybody, including you, can introduce his or her own parametrization of
the fields.
The nonlinear σ model is actually an example of a broad class of field theories whose
Lagrangian has a simple form but with the fields appearing in it subject to some nontrivial
constraint. An example is the theory defined by
L(U) =
f
2
4
tr(∂
μ
U
†
.
∂
μ
U) (4)
with U(x)a matrix-valued field and an element of SU(2). Indeed, if we write U =e
(i/f ) π
.
τ
we see that L(U ) =
1
2
(∂ π)
2
+ (1/2f
2
)( π
.
∂ π)
2
+
...
, identical to (3) up to the terms
indicated. The π field here is related to the one in (3) by a field redefinition.
There is considerably more we can say about the nonlinear σ models and their applica-
tions in particle and condensed matter physics, but a thorough discussion would take us
1
S. Weinberg, Physica 96A: 327, 1979.
VI.4. σ Models | 343
far beyond the scope of this book. Instead, I will develop some of their properties in the
exercises and in the next chapter will sketch how they can arise in one class of condensed
matter systems.
Exercises
VI.4.1 Show that the vacuum expectation value of (σ , π)can indeed point in any direction without changing the
physics. At first sight, this statement seems strange since, by virtue of its γ
5
coupling to the nucleon, the
pion is a pseudoscalar field and cannot have a vacuum expectation without breaking parity. But (σ , π)
are just Greek letters. Show that by a suitable transformation of the nucleon field parity is conserved, as
it should be in the strong interaction.
VI.4.2 Calculate the pion-pion scattering amplitude up to quadratic order in the external momenta, using the
nonlinear σ model (3). [Hint: For help, see S. Weinberg, Phys. Rev. Lett. 17: 616, 1966.]
VI.4.3 Calculate the pion-pion scattering amplitude up to quadratic order in the external momenta, using the
linear σ model (2). Don’t forget the Feynman diagram involving σ meson exchange. You should get the
same result as in exercise VI.4.2.
VI.4.4 Show that the mass relation M =gv amounts to the Goldberger-Treiman relation.

VI.5 Ferromagnets and Antiferromagnets
Magnetic moments
In chapters IV.1 and V.3 I discussed how the concept of the Nambu-Goldstone boson
originated as the spin wave in a ferromagnetic or an antiferromagnetic material. A cartoon
description of such materials consists of a regular lattice on each site of which sits a
local magnetic moment, which we denote by a unit vector n
j
with j labeling the site.
In a ferromagnetic material the magnetic moments on neighboring sites want to point
in the same direction, while in an antiferromagnetic material the magnetic moments
on neighboring sites want to point in opposite directions. In other words, the energy is
H =J
<ij>
n
i
.
n
j
, where i and j label neighboring sites. For antiferromagnets J>
0, and for ferromagnets J<0. I will merely allude to the fully quantum description
formulated in terms of a spin
S
j
operator on each site j ; the subject lies far beyond the
scope of this text.
In a more microscopic treatment, we would start with a Hamiltonian (such as the
Hubbard Hamiltonian) describing the hopping of electrons and the interaction between
them. Within some approximate mean field treatment the classical variable n
j
would then
emerge as the unit vector pointing in the direction of c
†
j
σc
j
with c
†
j
and c
j
the electron
creation and annihilation operators, respectively. But this is not a text on solid state physics.
First versus second order in time
Here we would like to derive an effective low energy description of the ferromagnet and
antiferromagnet in the spirit of the σ model description of the preceding chapter. Our
treatment will be significantly longer than the standard discussion given in some field
theory texts, but has the slight advantage of being correct.
The somewhat subtle issue is what kinetic energy term we have to add to −H to form the
Lagrangian L. Since for a unit vector n we have n
.
(d n/dt) = (d(n
.
n)/dt) =0, we cannot

VI.5. Magnetic Systems | 345
make do with one time derivative. With two derivatives we can form (d n/dt)
.
(d n/dt)
and so
L
wrong
=
1
2g
2
j
∂ n
j
∂t
.
∂ n
j
∂t
− J
<ij >
n
i
.
n
j
(1)
A typical field theory text would then pass to the continuum limit and arrive at the
Lagrangian density
L =
1
2g
2
(
∂ n
∂t
.
∂ n
∂t
− c
2
s
l
∂ n
∂x
l
.
∂ n
∂x
l
) (2)
with the constraint [n(x , t)]
2
= 1. This is another example of a nonlinear σ model. Just as
in the nonlinear σ model discussed in chapter VI.4, the Lagrangian looks free, but the
nontrivial dynamics comes from the constraint. The constant c
s
(which is determined in
terms of the microscopic variable J) is the spin wave velocity, as you can see by writing
down the equation of motion (∂
2
/∂t
2
)n − c
2
s
∇
2
n = 0.
But you can feel that something is wrong. You learned in a quantum mechanics course
that the dynamics of a spin variable
S is first order in time. Consider the most basic
example of a spin in a constant magnetic field described by H = μ
S
.
B. Then d
S/dt =
i[H ,
S] = μ
B ×
S. Besides, you might remember from a solid state physics course that in
a ferromagnet the dispersion relation of the spin wave has the nonrelativistic form ω ∝ k
2
and not the relativistic form ω
2
∝ k
2
implied by (2).
The resolution of this apparent paradox is based on the Pauli-Hopf identity: Given a unit
vector n we can always write n = z
†
σz, where z =
z
1
z
2
consists of two complex numbers
such that z
†
z ≡ z
†
1
z
1
+ z
†
2
z
2
= 1. Verify this! (A mathematical aside: Writing z
1
and z
2
out
in terms of real numbers we see that this defines the so-called Hopf map S
3
→S
2
.) While
we cannot form a term quadratic in n and linear in time derivative, we can write a term
quadratic in the complex doublet z and linear in time derivative. Can you figure it out
before looking at the next line?
The correct version of (1) is
L
correct
= i
j
z
†
j
∂z
j
∂t
+
1
2g
2
j
∂ n
j
∂t
.
∂ n
j
∂t
− J
<ij >
n
i
.
n
j
(3)
The added term is known as the Berry’s phase term and has deep topological meaning.
You should derive the equation of motion using the identity
dt δ
z
†
j
∂z
j
∂t
=
1
2
i
dt δn
j
.
n
j
×
∂ n
j
∂t
(4)
Remarkably, although z
†
j
(∂z
j
/∂t) cannot be written simply in terms of n
j
, its variation
can be.
Low energy modes in the ferromagnet and the antiferromagnet
In the ground state of a ferromagnet, the magnetic moments all point in the same
direction, which we can choose to be the z-direction. Expanding the equation of motion in
346 | VI. Field Theory and Condensed Matter
small fluctuations around this ground state n
j
=ˆe
z
+δ n
j
(where evidently ˆe
z
denotes the
appropriate unit vector) and Fourier transforming, we obtain
−
ω
2
g
2
+ h(k) −
1
2
iω
1
2
iω −
ω
2
g
2
+ h(k)
δn
x
(k)
δn
y
(k)
= 0 (5)
linking the two components δn
x
(k) and δn
y
(k) of δ n(k). The condition n
j
.
n
j
=1 says that
δn
z
(k) = 0. Here a is the lattice spacing and h(k) ≡ 4J [2 − cos(k
x
a) −cos(k
y
a)] 2Ja
2
k
2
for small k. (I am implicitly working in two spatial dimensions as evidenced by k
x
and k
y
.)
At low frequency the Berry term iω dominates the naive term ω
2
/g
2
, which we can
therefore throw away. Setting the determinant of the matrix equal to zero, we see that we
get the correct quadratic dispersion relation ω ∝ k
2
.
The treatment of the antiferromagnet is interestingly different. The so-called N
´
eel state
1
for an antiferromagnet is defined by n
j
=(−1)
j
ˆe
z
. Writing n
j
=(−1)
j
ˆe
z
+δ n
j
, we obtain
−
ω
2
g
2
+ f(k) −
1
2
iω
1
2
iω −
ω
2
g
2
+ f(k)
δn
x
(k)
δn
y
(k + Q)
= 0 (6)
linking δn
x
and δn
y
evaluated at different momenta. Here f(k) = 4J
[2 +cos(k
x
a) +cos(k
y
a)]and Q = [π/a, π/a]. The appearance of Q is due to (−1)
j
=e
iQaj
.
(I will let you figure out the somewhat overly compact notation.) The antiferromagnetic
factor (−1)
j
explicitly breaks translation invariance and kicks in the momentum Q when-
ever it occurs. A similar equation links δn
y
(k) and δn
x
(k + Q). Solving these equations,
you will find that there is a high frequency branch that we are not interested in and a low
frequency branch with the linear dispersion ω ∝ k.
Thus, the low frequency dynamics of the antiferromagnet can be described by the
nonlinear σ model (2), which when the spin wave velocity is normalized to 1 can be written
in the relativistic form:
L =
1
2g
2
∂
μ
n
.
∂
μ
n (7)
Exercises
VI.5.1 Work out the two branches of the spin wave spectrum in the ferromagnetic case, paying particular
attention to the polarization.
VI.5.2 Verify that in the antiferromagnetic case the Berry’s phase term merely changes the spin wave velocity
and does not affect the spectrum qualitatively as in the ferromagnetic case.
1
Note that while the N
´
eel state describes the lowest energy configuration for a classical antiferromagnet, it
does not describe the ground state of a quantum antiferromagnet. The terms S
+
i
S
−
j
+S
−
i
S
+
j
in the Hamiltonian
J
<ij>
S
i
.
S
j
flip the spins up and down.

VI.6 Surface Growth and Field Theory
In this chapter I will discuss a topic, rather unusual for a field theory text, taken from non-
equilibrium statistical mechanics, one of the hottest growth fields in theoretical physics
over the last few years. I want to introduce you to yet another area in which field theoretic
concepts are of use.
Imagine atoms being deposited randomly on some surface. This is literally how some
novel materials are grown. The height h(x , t) of the surface as it grows is governed by the
Kardar-Parisi-Zhang equation
∂h
∂t
= ν∇
2
h +
λ
2
(∇h)
2
+ η(x, t) (1)
This equation describes a deceptively simple prototype of nonequilibrium dynamics and
has a remarkably wide range of applicability.
To understand (1), consider the various terms on the right-hand side. The term ν∇
2
h
(with ν>0) is easy to understand: Positive in the valleys of h and negative on the peaks,
it tends to smooth out the surface. With only this term the problem would be linear and
hence trivial. The nonlinear term (λ/2)(∇h)
2
renders the problem highly nontrivial and
interesting; I leave it to you as an exercise to convince yourself of the geometric origin of
this term. The third term describes the random arrival of atoms, with the random variable
η(x , t) usually assumed to be Gaussian distributed, with zero mean,
1
and correlations
η(x, t)η(x
, t
)
= 2σ
2
δ
D
(x −x
)δ(t − t
) (2)
In other words, the probability distribution for a particular η(x , t) is given by
P(η) ∝ e
−
1
2σ
2
d
D
xdt η(x , t)
2
Here x represents coordinates in D-dimensional space. Experimentally, D = 2 for the
situation I described, but theoretically we are free to investigate the problem for any D.
1
There is no loss of generality here since an additive constant in η can be absorbed by the shift h → h + ct .
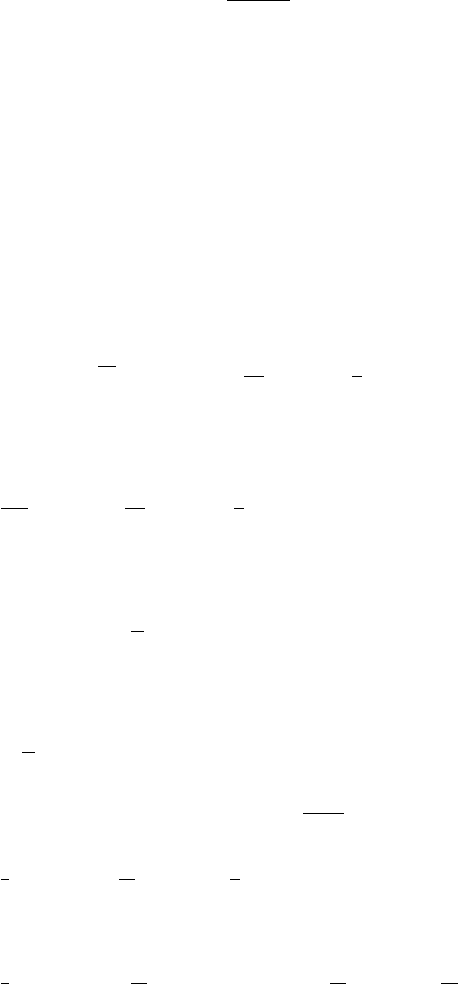
348 | VI. Field Theory and Condensed Matter
Typically, condensed matter physicists are interested in calculating the correlation be-
tween the height of the surface at two different positions in space and time:
[h(x, t) − h(x
, t
)]
2
=|x −x
|
2χ
f
|x −x
|
z
|t −t
|
, (3)
The bracket
...
here and in (2) denotes averaging over different realizations of the
random variable η(x , t). On the right-hand side of (3) I have written the dynamic scaling
form typically postulated in condensed matter physics, where χ and z are the so-called
roughness and dynamic exponents. The challenge is then to show that the scaling form is
correct and to calculate χ and z. Note that the dynamic exponent z (which in general is not
an integer) tells us, roughly speaking, how many powers of space is worth one power of
time. (For λ = 0 we have simple diffusion for which z = 2.) Here f denotes an unknown
function.
I will not go into more technical details. Our interest here is to see how this problem,
which does not even involve quantum mechanics, can be converted into a quantum field
theory. Start with
Z ≡
Dh
Dηe
−
1
2σ
2
d
D
xdt η(x , t)
2
δ
∂h
∂t
− ν∇
2
h −
λ
2
(∇h)
2
− η(x, t)
(4)
Integrating over η, we obtain Z =
Dhe
−S(h)
with the action
S(h) =
1
2σ
2
d
D
xdt
∂h
∂t
− ν∇
2
h −
λ
2
(∇h)
2
2
(5)
You will recognize that this describes a nonrelativistic field theory of a scalar field h(x , t).
The physical quantity we are interested in is then given by
h(x, t) − h(x
, t
)
2
=
1
Z
Dhe
−S(h)
[h(x, t) − h(x
, t
)]
2
(6)
Thus, the challenge of determing the roughness and dynamic exponents in statistical
physics is equivalent to the problem of determining the propagator
D(x, t) ≡
1
Z
Dhe
−S(h)
h(x, t )h(
0, 0)
of the scalar field h.
Incidentally, by scaling t → t/ν and h →
σ
2
/ν h, we can write the action as
S(h) =
1
2
d
D
xdt
∂
∂t
−∇
2
h −
g
2
(∇h)
2
2
(7)
with g
2
≡ λ
2
σ
2
/ν
3
. Expanding the action in powers of h as usual
S(h) =
1
2
d
D
xdt
∂
∂t
−∇
2
h
2
− g(∇h)
2
∂
∂t
−∇
2
h +
g
2
4
(∇h)
4
,
(8)
we recognize the quadratic term as giving us the rather unusual propagator 1/(ω
2
+ k
4
) for
the scalar field h, and the cubic and quartic term as describing the interaction. As always,

VI.6. Surface Growth | 349
h
h(x)
θ
d
cos θ
x
Figure VI.6.1
to calculate the desired physical quantity we evaluate the functional or “path” integral
Z =
Dhe
−S(h)+
d
D
xdtJ(x, t)h(x , t)
and then functionally differentiate repeatedly with respect to J .
My intent here is not so much to teach you nonequilibrium statistical mechanics as to
show you that quantum field theory can emerge in a variety of physical situations, including
those involving only purely classical physics. Note that the “quantum fluctuations” here
arise from the random driving term. Evidently, there is a close methodological connection
between random dynamics and quantum physics.
Exercises
VI.6.1 An exercise in elementary geometry: Draw a straight line tilted at an angle θ with respect to the horizontal.
The line represents a small segment of the surface at time t . Now draw a number of circles of diameter
d tangent to and on top of this line. Next draw another line tilted at angle θ with respect to the horizontal
and lying on top of the circles, namely tangent to them. This new line represents the segment of the
surface some time later (see fig. VI.6.1). Note that h = d/cos θ d(1 +
1
2
θ
2
). Show that this generates
the nonlinear term (λ/2)(∇h)
2
in the KPZ equation (1). For applications of the KPZ equation, see for
example, T. Halpin–Healy and Y.-C. Zhang, Phys. Rep. 254: 215, 1995; A. L. Barabasi and H. E. Stanley,
Fractal Concepts in Surface Growth.
VI.6.2 Show that the scalar field h has the propagator 1/(ω
2
+ k
4
).
VI.6.3 Field theory can often be cast into apparently rather different forms by a change of variable. Show that
by writing U = e
1
2
gh
we can change the action (7) to
S =
2
g
2
d
D
xdt
U
−1
∂
∂t
U − U
−1
∇
2
U
2
(9)
a kind of nonlinear σ model.

VI.7 Disorder: Replicas and Grassmannian Symmetry
Impurities and random potential
An important area in condensed matter physics involves the study of disordered systems,
a subject that has been the focus of a tremendous amount of theoretical work over the
last few decades. Electrons in real materials scatter off the impurities inevitably present
and effectively move in a random potential. In the spirit of this book I will give you a brief
introduction to this fascinating subject, showing how the problem can be mapped into a
quantum field theory.
The prototype problem is that of a quantum particle obeying the Schr
¨
odinger equa-
tion Hψ = [−∇
2
+ V(x)]ψ = Eψ, where V(x) is a random potential (representing the
impurities) generated with the Gaussian white noise probability distribution P(V)=
N e
−
d
D
x(1/2g
2
)V (x)
2
with the normalization factor N determined by
DV P (V ) =1. The
parameter g measures the strength of the impurities: the larger g, the more disordered the
system. This of course represents an idealization in which interaction between electrons
and a number of other physical effects are neglected.
As in statistical mechanics we think of an ensemble of systems each of which is charac-
terized by a particular function V(x)taken from the distribution P(V). We study the aver-
age or typical properties of the system. In particular, we might want to know the averaged
density of states defined by ρ(E) =tr δ(E − H)=
i
δ(E − E
i
), where the sum runs
over the ith eigenstate of H with corresponding eigenvalue E
i
. We denote by O(V)≡
DVP(V)O(V) the average of any functional O(V ) of V(x). Clearly,
E
∗
+δE
E
∗
dE ρ(E)
counts the number of states in the interval from E
∗
to E
∗
+δE, an important quantity in,
for example, tunneling experiments.
VI.7. Disorder | 351
Anderson localization
Another important physical question is whether the wave functions at a particular energy
E extend over the entire system or are localized within a characteristic length scale ξ(E).
Clearly, this issue determines whether the material is a conductor or an insulator. At first
sight, you might think that we should study
S(x, y; E) ≡
i
δ(E − E
i
)ψ
∗
i
(x)ψ
i
(y)
which might tell us how the wave function at x is correlated with the wave function at
some other point y, but S is unsuitable because ψ
∗
i
(x)ψ
i
(y) has a phase that depends on
V . Thus, S would vanish when averaged over disorder. Instead, the correct quantity to
study is
K(x − y; E) ≡
i
δ(E − E
i
)ψ
∗
i
(x)ψ
i
(y)ψ
∗
i
(y)ψ
i
(x)
since ψ
∗
i
(x)ψ
i
(y)ψ
∗
i
(y)ψ
i
(x) is manifestly positive. Note that upon averaging over all possi-
ble V(x)we recover translation invariance so that K does not depend on x and y separately,
but only on the separation |x −y|.As|x −y|→∞,ifK(x −y; E) ∼e
−|x−y|/ξ(E)
decreases
exponentially the wave functions around the energy E are localized over the so-called local-
ization length ξ(E). On the other hand, if K(x − y; E) decreases as a power law of |x −y|,
the wave functions are said to be extended.
Anderson and his collaborators made the surprising discovery that localization prop-
erties depend on D, the dimension of space, but not on the detailed form of P(V) (an
example of the notion of universality). For D = 1 and 2 all wave functions are localized,
regardless of how weak the impurity potential might be. This is a highly nontrivial state-
ment since a priori you might think, as eminent physicists did at the time, that whether the
wave functions are localized or not depends on the strength of the potential. In contrast, for
D = 3, the wave functions are extended for E in the range (−E
c
, E
c
).AsE approaches the
energy E
c
(known as the mobility edge) from above, the localization length ξ(E) diverges
as ξ(E)∼ 1/(E − E
c
)
μ
with some critical exponent
1
μ. Anderson received the Nobel Prize
for this work and for other contributions to condensed matter theory.
Physically, localization is due to destructive interference between the quantum waves
scattering off the random potential.
When a magnetic field is turned on perpendicular to the plane of a D = 2 electron gas
the situation changes dramatically: An extended wave function appears at E =0. For non-
zero E, all wave functions are still localized, but with the localization length diverging as
ξ(E) ∼ 1/|E|
ν
. This accounts for one of the most striking features of the quantum Hall
effect (see chapter VI.2): The Hall conductivity stays constant as the Fermi energy increases
but then suddenly jumps by a discrete amount due to the contribution of the extended state
1
This is an example of a quantum phase transition. The entire discussion is at zero temperature. In contrast
to the phase transition discussed in chapter V.3, here we vary E instead of the temperature.
