Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

372 | VII. Grand Unification

the group element that defines the gauge transformation at x and is obviously not to be

confused with the coupling constant.)

Since (A) appears in (3) multiplied by δ[f (A)], in the integral over g we expect, for

a reasonable choice of f (A), only infinitesimal g to be relevant. Let us choose f (A) =

∂A − σ . Under an infinitesimal transformation, A

→ A

− f

abc

+ ∂

and thus

(A) ={



Dθδ[∂A

− σ

− ∂

abc

− ∂

)]}

−1

(4)

“ = ” {



Dθδ[∂

abc

− ∂

)]}

−1

where the “effectively equal sign” follows since (A) is to be multiplied later by δ[f (A)].

Let us write formally

∂

abc

− ∂

) =



(x, y)θ

(y) (5)

thus defining the operator K

(x, y) =∂

abc

− ∂

)δ

(4)

(x − y). Note that in con-

trast to electromagnetism here K depends on the gauge potential. The elementary result



dθδ(Kθ) =1/K for θ and K real numbers can be generalized to



dθδ(Kθ) =1/ det K

for θ a real vector and K a nonsingular matrix. Regarding K

(x, y) as a matrix, we ob-

tain (A) = det K , but we know from chapter II.5 how to represent the determinant as a

functional integral over Grassmann variables: Write (A) =



DcDc

†

ghost

†

, c)

, with

ghost

†

, c) =



†

(x)K

(x, y)c

(y)



x[∂c

†

(x)∂c

(x) − ∂

†

(x)f

abc

(x)c

(x)]



x∂c

†

(x)Dc

(x) (6)

and with D the covariant derivative for the adjoint representation, to which the fields c

and c

†

belong just like A

. The fields c

and c

†

are known as ghost fields because they

violate the spin-statistics connection: Though scalar, they are treated as anticommuting.

This “violation” is acceptable because they are not associated with physical particles and

are introduced merely to represent (A) in a convenient form.

This takes care of the (A) factor in (3). As for the δ[f (A)] factor, we use the same trick

as in chapter III.4 and integrate Z over σ

(x) with a Gaussian weight e

−(i/2ξ)



xσ

(x)

so that δ[f (A)] gets replaced by e

−(i/2ξ)



x(∂A

)

Putting it all together, we obtain

Z =



DADcDc

†

iS(A)−(i/2ξ)



x(∂A)

+iS

ghost

†

, c)

(7)

with ξ a gauge parameter. Comparing with the corresponding expression for an abelian

gauge theory in chapter III.4, we see that in nonabelian gauge theories we have a ghost

action S

ghost

in addition to the Yang-Mills action. Thus, L

and L

are changed to

=−

(∂

− ∂

)

−

2ξ

(∂

)

+ ∂c

†

∂c

(8)

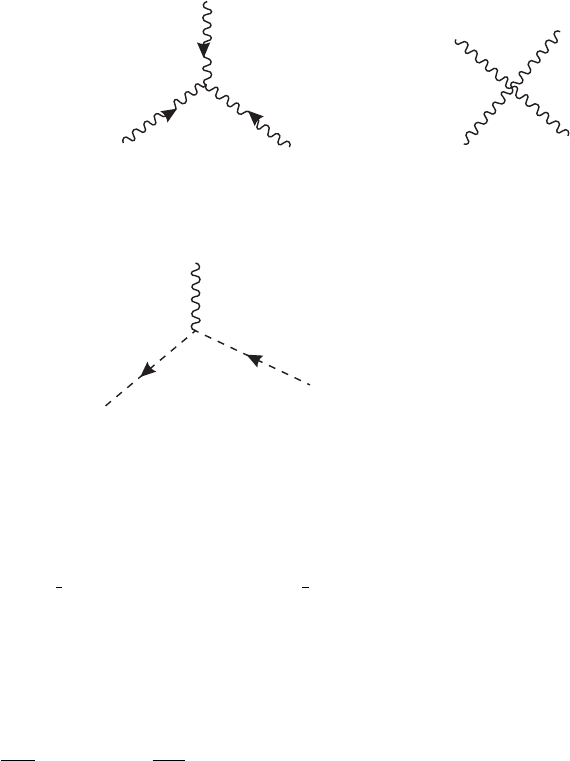
VII.1. Quantizing Yang-Mills Theory | 373

c,λ

b,ν

d,ρ

c,λ

(a) (b)

(c)

Figure VII.1.1

and

=−

g(∂

− ∂

abc

bμ

cν

abc

ade

dμ

eν

− ∂

†

abc

(x) (9)

We can now read off the propagators for the gauge boson and for the ghost field imme-

diately from (8). In particular, we see that except for the group index a the terms quadratic

in the gauge potential are exactly the same as the terms quadratic in the electromagnetic

gauge potential in (III.4.8). Thus, the gauge boson propagator is

(−i)



νλ

− (1 − ξ)



(10)

Compare with (III.4.9). From the term ∂c

†

∂c

in (8) we find the ghost propagator to be

(i/k

)δ

From L

we see that there is a cubic and a quartic interaction between the gauge

bosons, and an interaction between the gauge boson and the ghost field, as illustrated

in figure VII.1.1. The cubic and the quartic couplings can be easily read off as

abc

μν

− k

)

+ g

νλ

− k

)

+ g

λμ

− k

)

] (11)

and

−ig

abe

cde

μλ

νρ

− g

μρ

νλ

) + f

ade

cbe

μλ

νρ

− g

μν

ρλ

)

+ f

ace

bde

μν

λρ

− g

μρ

νλ

)] (12)

respectively. The coupling to the ghost field is

abc

(13)

374 | VII. Grand Unification

Obviously, we can exploit various permutation symmetries in writing these down. For

instance, in (12) the second term is obtained from the first by the interchange {c, λ}↔

{d , ρ}, and the third and fourth terms are obtained from the first and second by the

interchange {a, μ}↔{c, λ}.

Unnatural act

In a highly symmetric theory such as Yang-Mills, perturbating is clearly an unnatural

act as it involves brutally splitting L into two parts: a part quadratic in the fields and

the rest. Consider, for example, an exactly soluble single particle quantum mechanics

problem, such as the Schr

odinger equation with V(x)= 1 −(1/ cosh x)

. Imagine writing

V(x)=

+ W(x) and treating W(x) as a perturbation on the harmonic oscillator. You

would have a hard time reproducing the exact spectrum, but this is exactly how we brutalize

Yang-Mills theory in the perturbative approach: We took the “holistic entity” tr F

μν

and

split it up into the “harmonic oscillator” piece tr(∂

− ∂

)

and a “perturbation.”

If Yang-Mills theory ever proves to be exactly soluble, the perturbative approach with its

mangling of gauge invariance is clearly not the way to do it.

Lattice gauge theory

Wilson proposed a way out: Do violence to Lorentz invariance rather than to gauge in-

variance. Let us formulate Yang-Mills theory on a hypercubic lattice in 4-dimensional

Euclidean spacetime. As the lattice spacing a → 0 we expect to recover 4-dimensional

rotational invariance and (by a Wick rotation) Lorentz invariance. Wilson’s formulation,

known as lattice gauge theory, is easy to understand, but the notation is a bit awkward, due

to the lack of rotational invariance. Denote the location of the lattice sites by the vector x

On each link, say the one going from x

to one of its nearest neighbors x

, we associate an

N by N simple unitary matrix U

. Consider the square, known as a plaquette, bounded

by the four corners x

, x

, and x

(with these nearest neighbors to each other.) See

figure VII.1.2. For each plaquette P we associate the quantity S(P) = Re tr U

constructed to be invariant under the local transformation

→ V

†

(14)

The symmetry is local because for each site x

we can associate an independent V

Wilson defined Yang-Mills theory by

Z =



dU e

(1/2f

)



S(P)

(15)

where the sum is taken over all the plaquettes in the lattice. The coupling strength f

controls how wildly the unitary matrices U

’s fluctuate. For small f , large values of S(P)

are favored, and so the U

’s are all approximately equal to the unit matrix (up to an

irrelevant global transformation.)

VII.1. Quantizing Yang-Mills Theory | 375

Figure VII.1.2

Without doing any arithmetic, we can argue by symmetry that in the continuum limit

a → 0, Yang-Mills theory as we know it must emerge: The action is manifestly invariant

under local SU (N) transformation. To actually see this, define a field A

(x) with μ =

1, 2, 3, 4, permeating the 4-dimensional Euclidean space the lattice lives in, by

= V

†

iaA

(x)

(16)

where x =

+ x

) (namely the midpoint of the link U

lives on) and μ is the direction

connecting x

to x

(namely ˆμ ≡ (x

−x

)/a is the unit vector in the μ direction.) The V ’s

just reflect the gauge freedom in (14) and obviously do not enter into the plaquette action

S(P) by construction. I will let you show in an exercise that

tr U

= tr e

μν

+O(a

)

(17)

with F

μν

the Yang-Mills field strength evaluated at the center of the plaquette. Indeed, we

could have discovered the Yang-Mills field strength in this way. I hope that you start to

see the deep geometric significance of F

μν

. Continuing the exercise you will find that the

action on each plaquette comes out to be

S(P ) =Re tr e

μν

+O(a

)

= Re tr[1 + ia

μν

−

μν

+ O(a

)] =tr 1 −

tr F

μν

...

(18)

and so up to an irrelevant additive constant we recover in (15) the Yang-Mills action in the

continuum limit. Again, it is worth emphasizing that without going through any arithmetic

we could have fixed the a

term in (18) (up to an overall constant) by dimensional analysis

and gauge invariance.

The sign can be easily checked against the abelian case.

376 | VII. Grand Unification

The Wilson formulation is beautiful in that none of the hand-wringing over gauge

fixing, Faddeev-Popov determinant, ghost fields, and so forth is necessary for (15) to make

sense. Recalling chapter V.3 you see that (15) defines a statistical mechanics problem

like any other. Instead of integrating over some spin variables say, we integrate over the

group SU (N) for each link. Most importantly, the lattice gauge formulation opens up

the possibility of computing the properties of a highly nontrivial quantum field theory

numerically. Lattice gauge theory is a thriving area of research. For a challenge, try to

incorporate fermions into lattice gauge theory: This is a difficult and ongoing problem

because fermions and spinor fields are naturally associated with SO(4), which does not

sit well on a lattice.

Wilson loop

Field theorists usually deal with local observables, that is, observables defined at a space-

time point x , such as J

(x) or tr F

μν

(x)F

μν

(x), but of course we can also deal with

nonlocal observables, such as e



in electromagnetism, where the line integral is

evaluated over a closed curve C . The gauge invariant quantity in the exponential is equal

to the electromagnetic flux going through the surface bounded by C. (Indeed, recall chap-

ter IV.4.)

Wilson pointed out that lattice gauge theory contains a natural gauge invariant but

nonlocal observable W(C) ≡tr U

...U

, where the set of links connecting x

to x

et cetera and eventually to x

and back to x

traces out a loop called C. Referring

to (16) we see that W(C), known as the Wilson loop, is the trace of a product of many

factors of e

iaA

. Thus, in the continuum limit a → 0, we have evidently

W(C) ≡tr Pe



(19)

with C now an arbitrary curve in Euclidean spacetime. Here P denotes path ordering,

clearly necessary since the A

’s associated with different segments of C , being matrices,

do not commute with each other. [Indeed, P is defined by the lattice definition of W(C).]

To understand the physical meaning of the Wilson loop, Recall chapters I.4 and I.5. To

obtain the potential energy E between two oppositely charged lumps we have to compute

lim

T →∞



DAe

Maxwell

(A)+i



= e

−iET

For two lumps held at a distance R apart we plug in

(x) = η

μ0

{δ

(3)

(x)− δ

(3)

[x − (R,0,0)]}

and see that we are actually computing the expectation value e



−



)

 in

a fluctuating electromagnetic field, where C

and C

denote two straight line segments

at x = (0, 0, 0) and x =(R,0,0), respectively. It is convenient to imagine bringing the

two lumps together in the far future (and similarly in the far past). Then we deal instead

with the manifestly gauge invariant quantity e



, where C is the rectangle shown

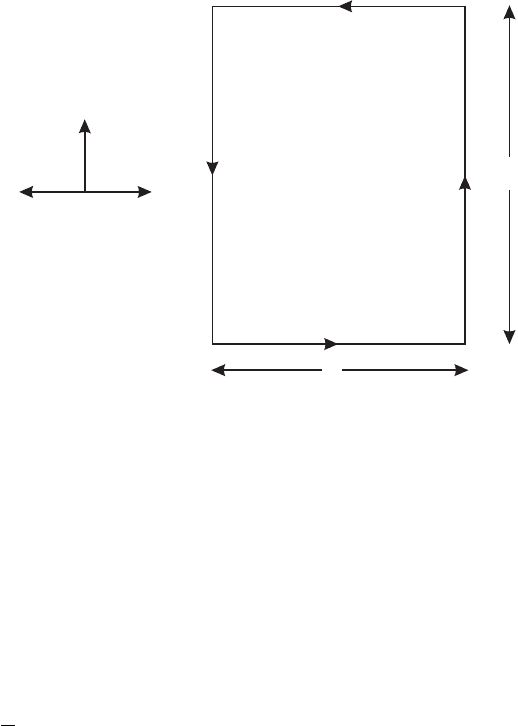
VII.1. Quantizing Yang-Mills Theory | 377

Time

Space

Figure VII.1.3

in figure VII.1.3. Note that for T large loge



∼−iE(R)T , which is essentially

proportional to the perimeter length of the rectangle C.

As we will discuss in chapter VII.3 and as you have undoubtedly heard, the currently

accepted theory of the strong interaction involves quarks coupled to a nonabelian Yang-

Mills gauge potential A

. Thus, to determine the potential energy E(R) between a quark

and an antiquark held fixed at a distance R from each other we “merely” have to compute

the expectation value of the Wilson loop

W(C)=



dU e

−(1/2f

)



S(P)

W(C) (20)

In lattice gauge theory we could compute logW(C) for C the large rectangle in fig-

ure VII.1.3 numerically, and extract E(R). (We lost the i because we are living in Euclidean

spacetime for the purpose of this discussion.)

Quark confinement

You have also undoubtedly heard that since free quarks have not been observed, quarks are

generally believed to be permanently confined. In particular, it is believed that the potential

energy between a quark and an antiquark grows linearly with separation E(R) ∼ σR.

One imagines a string tying the quark to the antiquark with a string tension σ . If this

conjecture is correct, then logW(C)∼σRT should go as the area RT enclosed by C.

Wilson calls this behavior the area law, in contrast to the perimeter law characteristic of

familiar theories such as electromagnetism. To prove the area law in Yang-Mills theory is

one of the outstanding challenges of theoretical physics.

378 | VII. Grand Unification

Exercises

VII.1.1 The gauge choice in the text preserves Lorentz invariance. It is often useful to choose a gauge that breaks

Lorentz invariance, for example, f (A) =n

(x) with n some fixed 4-vector. This class of gauge choices,

known as the axial gauge, contains various popular gauges, each of which corresponds to a particular

choice of n. For instance, in light-cone gauge, n = (1, 0, 0, 1), in space-cone gauge, n = (0, 1, i ,0). Show

that for any given A(x) we can find a gauge transformation so that n



(x) = 0.

VII.1.2 Derive (17) and relate f to the coupling g in the continuum formulation of Yang-Mills theory. [Hint: Use

the Baker-Campbell-Hausdorff formula

= e

A+B+

[A, B]+

([A,[A, B]]+[B ,[B , A]] )+

...

VII.1.3 Consider a lattice gauge theory in (D + 1)-dimensional space with the lattice spacing a in D-dimensional

space and b in the extra dimension. Obtain the continuum D-dimensional field theory in the limit a →0

with b kept fixed.

VII.1.4 Study in (2) the alternative limit b → 0 with a kept fixed so that you obtain a theory on a spatial lattice

but with continuous time.

VII.1.5 Show that for lattice gauge theory the Wilson area law holds in the limit of strong coupling. [Hint: Expand

(20) in powers of f

−2

VII.2 Electroweak Unification

The scourge of massless spin 1 particles

With the benefit of hindsight, we now know that Nature likes Yang-Mills theory. In the

late 1960s and early 1970s, the electromagnetic and weak interactions were unified into

an electroweak interaction, described by a nonabelian gauge theory based on the group

SU(2) ⊗ U(1). Somewhat later, in the early 1970s, it was realized that the strong interaction

can be described by a nonabelian gauge theory based on the group SU(3). Nature literally

consists of a web of interacting Yang-Mills fields.

But when the theory was first proposed in 1954, it seemed to be totally inconsistent with

observations as they were interpreted at that time. As Yang and Mills themselves pointed

out in their paper, the theory contains massless spin 1 particles, which were certainly not

known experimentally. Thus, except for interest on the part of a few theorists (Schwinger,

Glashow, Bludman, and others) who found the mathematical structure elegantly attractive

and felt that nonabelian gauge theory must somehow be relevant for the weak interaction,

the theory gradually sank into oblivion and was not part of the standard graduate curricu-

lum in particle physics in the 1960s.

Again with the benefit of hindsight, it would seem that there are only two logical

solutions to the difficulty that experimentalists do not see any massless spin 1 particles

except for the photon: (1) the Yang-Mills particles somehow acquire mass, or (2) the Yang-

Mills particles are in fact massless but are somehow not observed. We now know that the

first possibility was realized in the electroweak interaction and the second in the strong

interaction.

Constructing the electroweak theory

We now discuss electroweak unification. It is perhaps pedagogically clearest to motivate

how we would go about constructing such a theory. As I have said before, this is not a

380 | VII. Grand Unification

textbook on particle physics and I necessarily will have to keep the discussion of particle

physics to the bare minimum. I gave you a brief introduction to the structure of the weak

interaction in chapter IV.2. The other salient fact is that weak interaction violates parity,

as mentioned in chapter II.1. In particular, the left handed electron field e

and the right

handed electron field e

, which transform into each other under parity, enter into the weak

interaction quite differently.

Let us start with the weak decay of the muon, μ

−

→ e

−

+¯ν + ν



, with ν and ν



the

electron neutrino and muon neutrino, respectively. The relevant term in the Lagrangian

is ¯ν



¯e

, with the left hand electron field e

, the electron neutrino field (which

is left handed) ν

, and so forth. The field μ

annihilates a muon, the field ¯e

creates an

electron, and so on. (Henceforth, we will suppress the word field.) As you probably know,

the elementary constituents of matter form three families, with the first family consisting

of ν , e, and the up u and down d quarks, the second of ν



, μ, and the charm c and strange

s quarks, and so on. For our purposes here, we will restrict our attention to the first family.

Thus, we start with ¯ν

¯e

As I remarked in chapter III.2, a Fermi interaction of this type can be generated by the

exchange of an intermediate vector boson W

with the coupling W

¯ν

−

¯e

The idea is then to consider an SU(2) gauge theory with a triplet of gauge bosons denoted

by W

, with a = 1, 2, 3 . Put ν

and e

into the doublet representation and the right handed

electron field e

into a singlet representation, thus

≡





, e

(1)

(The notation is such that the upper component of ψ

is ν

and the lower component is

The fields ν

and e

, but not e

, listen to the gauge bosons W

. Indeed, according to

(IV.5.21) the Lagrangian contains

= (W

1−i2

1+i2

+ h.c.) + W

where W

1−i2

≡ W

− iW

and so forth. We recognize τ

1+i2

≡ τ

+ iτ

as the raising

operator and the first two terms as (W

1−i2

¯ν

+ h.c.), precisely what we want. By

design, the exchange of W

generates the desired term ¯ν

¯e

We need more room

We would hope that the boson W

we were forced to introduce would turn out to be the pho-

ton so that electromagnetism is included. But alas, W

couples to the current

(¯ν

−¯e

), not the electromagnetic current −( ¯e

+¯e

). Oops!

Another problem lurks. To generate a mass term for the electron, we need a doublet

Higgs field ϕ ≡





in order to construct the SU(2) invariant term f

ϕe

in the

Lagrangian so that when ϕ acquires the vacuum expectation value





we will have

VII.2. Electroweak Unification | 381

ϕe

→ f(¯ν, ¯e)





= fv¯e

(2)

But none of the SU(2) transformations leaves





invariant: The vacuum expectation value

of ϕ spontaneously breaks the entire SU(2) symmetry, leaving all three W bosons massive.

There is no room for the photon in this failed theory. Aagh!

We need more room. Remarkably, we can avoid both the oops and the aagh by extending

the gauge symmetry to SU(2) ⊗ U(1). Denoting the generator of U(1) by

Y (called the

hypercharge) and the associated gauge potential by B

[and their counterparts T

and W

for SU(2)] we have the covariant derivative D

=∂

−igW

−ig



. With four gauge

bosons, we dare to hope that one of them might turn out to be the photon.

The gauge potentials are normalized by the corresponding kinetic energy terms,

L =−

μν

)

−

μν

)

...

with the abelian B

μν

=∂

−∂

and nonabelian field

strength W

μν

=∂

−∂

+ε

abc

. The generators T

are of course normalized

by the commutation relations that define SU(2). In contrast, there is no commutation

relation in the abelian algebra U(1) to fix the normalization of the generator

Y . Until this

is fixed, the normalization of the U(1) gauge coupling g



is not fixed.

How do we fix the normalization of the generator

Y ? By construction, we want spon-

taneous symmetry breaking to leave a linear combination of T

and

Y invariant, to be

identified as the generator the massless photon couples to, namely the charge operator Q.

Thus, we write

Q = T

Y (3)

Once we know T

and

Y of any field, this equation tells us its charge. For example,

Q(ν

) =

Y(ν

) and Q(e

) =−

Y(e

). In particular, we see that the coefficient

of T

in (3) must be 1 since the charges of ν

and e

differ by 1. The relation (3) fixes the

normalization of

Y .

Determining the hypercharge

The next step is to determine the hypercharge of various multiplets in the theory, which in

turn determines how B

couples to these multiplets. Consider ψ

.Fore

to have charge

−1, the doublet ψ

must have

Y =−

. In contrast, the field e

has

Y =−1 since T

on e

Given the hypercharge of ψ

and e

we see that the invariance of the term f

ϕe

under SU(2) ⊗ U(1) forces the Higgs field ϕ to have

Y =+

. Thus, according to (3)

the upper component of ϕ has electric charge Q =+

=+1 and the lower component

Q =−

=0. Thus, we write ϕ =





. Recall that ϕ has the vacuum expectation value





. The fact that the electrically neutral field ϕ

acquires a vacuum expectation value but

the charged field ϕ

does not provide a consistency check.