Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

392 | VII. Grand Unification

QCD

g(μ)

4π

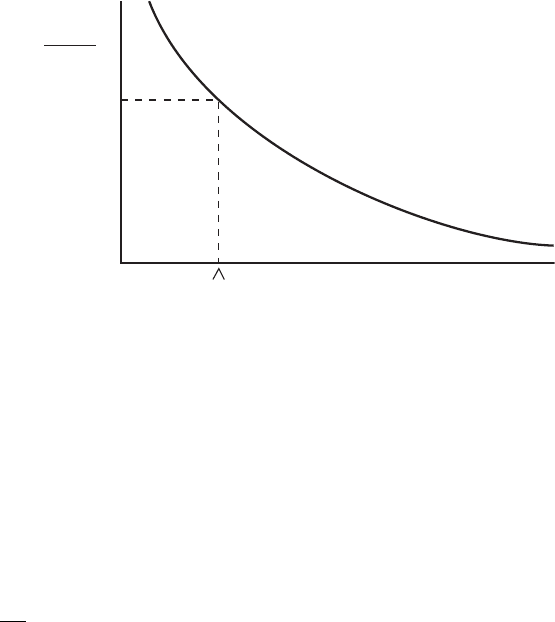
Figure VII.3.6

theory turns out to be exactly soluble, pure Yang-Mills, with all its fabulous symmetries,

is the most likely possibility. (Perhaps an even more likely candidate for solubility is

supersymmetric Yang-Mills theory. We will touch on supersymmetry in chapter VIII.4.)

Let me be specific about what it means to solve QCD. Consider a world with only up

and down quarks with m

and m

both set equal to zero, namely a world described by

L =−

μν

aμν

+¯qiγ

q (10)

The goal would be to calculate something like the ratio of the mass of the ρ meson m

the mass of the proton m

To make progress, theoretical physicists typically need to have a small parameter to

expand in, but in trying to solve (10) we are confronted with the immediate difficulty

that there is no such parameter. You might think that g is a parameter, but you would

be mistaken. The renormalization group analysis taught us that g(μ) is a function of the

energy scale μ at which it is measured. Thus, there is no particular dimensionless number

we can point to and say that it measures the strength of QCD. Instead, the best we can do

is to point to the value of μ at which (g(μ)

/4π) becomes of order 1. This is the energy,

known as 

QCD

, at which the strong interaction becomes strong as we come down from

high energy (fig. VII.3.6). But 

QCD

merely sets the scale against which other quantities

are to be measured. In other words, if you manage to calculate m

it better come out

proportional to 

QCD

since 

QCD

is the only quantity with dimension of mass around.

Similarly for m

. Put in precise terms, if you publish a paper with a formula giving m

in terms of pure numbers such as 2 and π , the field theory community will hail you as a

conquering hero who has solved QCD exactly.

The apparent trade of a dimensionless coupling g for a dimensional mass scale 

QCD

is known as dimensional transmutation, of which we will see another example in the next

chapter.

VII.3. Quantum Chromodynamics | 393

Exercises

VII.3.1 Calculate C in (9). [Hint: If you need help, consult T. Appelquist and H. Georgi, Phys. Rev. D8: 4000, 1973;

and A. Zee, Phys. Rev. D8: 4038, 1973.]

VII.3.2 Calculate (2).

VII.4 Large N Expansion

Inventing an expansion parameter

Quantum chromodynamics is a zero-parameter theory, so it is difficult to give even a first

approximation. In desperation, field theorists invented a parameter in which to expand

QCD. Suppose instead of three colors we have N colors. ’t Hooft

noticed that as N →∞

remarkable simplifications occur. The idea is that if we can calculate m

, for example,

in the large N limit the result may be close to the actual value. People sometimes joke that

particle physicists regard 3 as a large number, but actually the correction to the large N

limit is typically of order 1/N

, about 10% in the real world. Particle physicists would be

more than happy to be able to calculate hadron masses to this degree of accuracy.

As with spontaneous symmetry breaking and a number of other important concepts, the

large N expansion came out of condensed matter physics but nowadays is used routinely

in all sorts of contexts. For example, people have tried a large N approach to solve high-

temperature superconductivity and to fold RNA.

Scaling the QCD coupling

So, let the color group be U(N) and write

L =−

tr F

μν

ψ[i(∂ − iA) − m]ψ (1)

Note that we have replaced g

by g

. For finite N this change has no essential signifi-

cance. The point is to choose the power a so that interesting simplifications occur in the

limit N →∞with g

held fixed. The cubic and quartic interaction vertices of the gluons

G. ’t Hooft, Under the Spell of the Gauge Principle, p. 378.

M. Bon, G. Vernizzi, H. Orland, and A. Zee, “Topological classification of RNA structures,” J. Mol. Biol.

379:900, 2008.

VII.4. Large N Expansion | 395

γγγγ

(a) (b)

Figure VII.4.1

are proportional to N

. On the other hand, since the gluon propagator goes as the inverse

of the quadratic terms in L, it is proportional to 1/N

. The coupling of the gluon to the

quark does not depend on N .

To fix a, let us focus on a specific application, the calculation of σ(e

−

→ hadrons)

discussed in the last chapter. Suppose we want to calculate this cross section at low

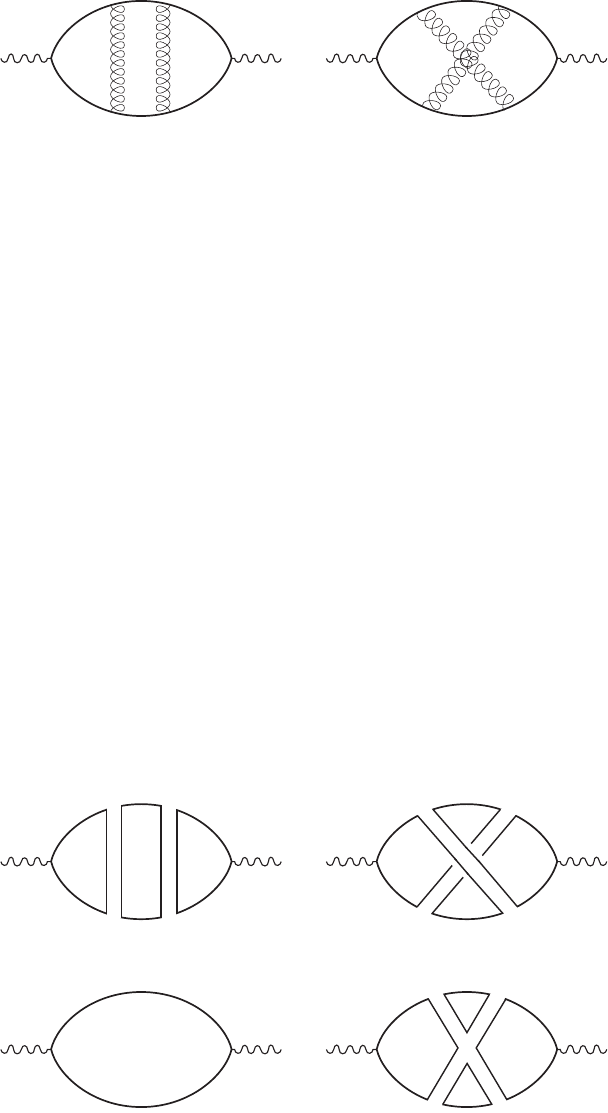
energies. Consider the two-gluon exchange diagrams shown in figures VII.4.1a and b.

The two diagrams are of order g

and we would have to calculate both. Note that 1b is

nonplanar: Since one gluon crosses over the other, the diagram cannot be drawn on the

plane if we insist that lines cannot go through each other.

Now the double-line formalism introduced in chapter IV.5 shines. In this formalism

the diagrams figure VII.4.1a and b are redrawn as in figure VII.4.2a and b. The two gluon

propagators common to both diagrams give a factor 1/N

. Now comes the punchline.

We sum over three independent color indices in 2a, thus getting a factor N

. Grab some

crayons and try to color each line in 2a with a different color: you will need three crayons.

In contrast, we sum over only one independent index in 2b, getting only a factor of N.In

other words, 2a dominates 2b by a factor N

. In the large N limit we can throw 2b away.

Clearly, the rule is to associate one factor of N with each loop. Thus, the lowest order

diagram, shown in 2c, with N different colors circulating in it, scales as N; 2a scales as

. We want 2a and 2c to scale in the same way and thus we choose a = 1.

(a)

(b)

(c)

(d)

Figure VII.4.2

396 | VII. Grand Unification

By drawing more diagrams [e.g., 2d scales as N(1/N

, with the three factors coming

from the quartic coupling, the propagators, and the sum over colors, respectively], you can

convince yourself that planar diagrams dominate in the large N limit, all scaling as N.For

a challenge, try to prove it. Evidently, there is a topological flavor to all this.

The reduction to planar diagrams is a vast simplification but there are still an infinite

number of diagrams. At this stage in our mastery of field theory, we still can’t solve large

N QCD. (As I started writing this book, there were tantalizing clues, based on insight and

techniques developed in string theory, that a solution of large N QCD might be within

sight. As I now go through the final revision, that hope has faded.)

The double-line formalism has a natural interpretation. Group theoretically, the matrix

gauge potential A

transforms just like ¯q

(but assuredly we are not saying that the gluon

is a quark-antiquark bound state) and the two lines may be thought of as describing a quark

and an antiquark propagating along, with the arrows showing the direction in which color

is flowing.

Random matrix theory

There is a much simpler theory, structurally similar to large N QCD, that actually can be

solved. I am referring to random matrix theory.

Exaggerating a bit, we can say that quantum mechanics consists of writing down a

matrix known as the Hamiltonian and then finding its eigenvalues and eigenvectors. In the

early 1950s, when confronted with the problem of studying the properties of complicated

atomic nuclei, Eugene Wigner proposed that instead of solving the true Hamiltonian in

some dubious approximation we might generate large matrices randomly and study the

distribution of the eigenvalues—a sort of statistical quantum mechanics. Random matrix

theory has since become a rich and flourishing subject, with an enormous and growing

literature and applications to numerous areas of theoretical physics and even to pure

mathematics (such as operator algebra and number theory.)

It has obvious applications

to disordered condensed matter systems and less obvious applications to random surfaces

and hence even to string theory. Here I will content myself with showing how ’t Hooft’s

observation about planar diagrams works in the context of random matrix theory.

Let us generate N by N hermitean matrices ϕ randomly according to the probability

P(ϕ)=

−N tr V(ϕ)

(2)

with V(ϕ) a polynomial in ϕ. For example, let V(ϕ)=

+ gϕ

. The normalization



dϕP(ϕ) = 1 fixes

Z =



dϕe

−N tr V(ϕ)

(3)

The limit N →∞is always understood.

For a glimpse of the mathematical literature, see D. Voiculescu, ed., Free Probability Theory .

VII.4. Large N Expansion | 397

As in chapter VI.7 we are interested in ρ(E), the density of eigenvalues of ϕ. To make

sure that you understand what is actually meant, let me describe what we would do were

we to evaluate ρ(E) numerically. For some large integer N , we would ask the computer to

generate a hermitean matrix ϕ with the probability P(ϕ)and then to solve the eigenvalue

equation ϕv =Ev. After this procedure had been repeated many times, the computer could

plot the distribution of eigenvalues in a histogram that eventually approaches a smooth

curve, called the density of eigenvalues ρ(E).

We already developed the formalism to compute ρ(E) in (VI.7.1): Compute the real

analytic function G(z) ≡(1/N) tr[1/(z − ϕ)]and ρ(E) =−(1/π) lim

ε→0

Im G(E + iε). The

average 

...

 is taken with the probability P(ϕ):

O(ϕ)=



Dϕe

−NtrV(ϕ)

O(ϕ)

You see that my choice of notation, ϕ for the matrix and V(ϕ)=

+ gϕ

as an

example, is meant to be provocative. The evaluation of Z is just like the evaluation of a path

integral, but for an action S(ϕ) = N tr V(ϕ)that does not involve



x. Random matrix

theory can be thought of as a quantum field theory in (0 + 0)-dimensional spacetime!

Various field theoretic methods, such as Feynman diagrams, can all be applied to

random matrix theory. But life is sweet in (0 + 0)-dimensional spacetime: There is no

space, no time, no energy, and no momentum and hence no integral to do in evaluating

Feynman diagrams.

The Wigner semicircle law

Let us see how this works for the simple case V(ϕ)=

(we can always absorb m into

ϕ but we won’t). Instead of G(z), it is slightly easier to calculate

(z) ≡



z − ϕ



= δ

G(z)

The last equality follows from invariance under unitary transformations:

P(ϕ)= P(U

†

ϕU) (4)

Expand

(z) =

∞



n=0

2n+1

(ϕ

)

 (5)

Do the Gaussian integral



dϕe

−N tr



dϕe

−N



p, q

= δ

(6)

Setting k = l and summing, we find the n = 1 term in (5) is equal to (1/z

)δ

(1/m

Just as in any field theory we can associate a Feynman diagram with each of the terms

in (5). For the n = 1 term, we have figure VII.4.3. The matrix character of ϕ lends itself

naturally to ’t Hooft’s double-line formalism and thus we can speak of quark and gluon

398 | VII. Grand Unification

jlki

Figure VII.4.3

propagators with a good deal of ease. The Feynman rules are given in figure VII.4.4. We

recognize ϕ as the gluon field and (5) as the gluon propagator. Indeed, we can formulate

our problem as follows: Given the bare quark propagator 1/z, compute the true quark

propagator G(z) with all interaction effects taken into account.

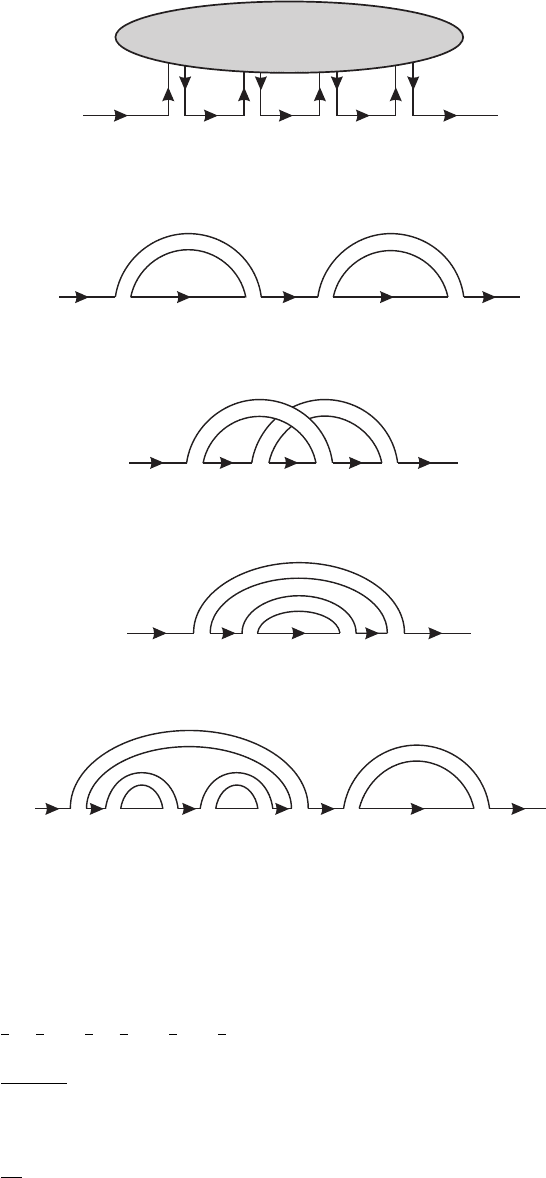
Let us now look at the n = 2 term in (5) 1/z

<ϕ

>, which we represent in

figure VII.4.5a. With a bit of thought you can see that the index i can be contracted with

k, l,orj , thus giving rise to figures VII.4.5b, c, d. Summing over color indices, just as in

QCD, we see that the planar diagrams in 5b and 5d dominate the diagram in 5c by a factor

. We can take over ’t Hooft’s observation that planar diagrams dominate.

Incidentally, in this example, you see how large N is essential, allowing us to get rid of

nonplanar diagrams. After all, if I ask you to calculate the density of eigenvalues for say

N =7 you would of course protest saying that the general formula for solving a degree-7

polynomial equation is not even known.

The simple example in figure VII.4.5 already indicates how all possible diagrams could

be constructed. In 5b the same “unit” is repeated, while in 5d the same “unit” is nested

inside a more basic diagram. A more complicated example is shown in 5e. You can convince

yourself that for N =∞all diagrams contributing to G(z) can be generated by either

“nesting” existing diagrams inside an overarching gluon propagator or “repeating” an

Figure VII.4.4

VII.4. Large N Expansion | 399

ihjlk

(a)

(b)

(c)

(d)

(e)

Figure VII.4.5

existing structure over and over again. Translate the preceding sentence into two equations:

“Repeat” (see figure VII.4.6a),

G(z) =

(z)

...

z − (z)

(7)

and “nest” (see figure VII.4.6b),

(z) =

G(z) (8)

400 | VII. Grand Unification

Σ Σ

(a)

(b)

Figure VII.4.6

Combining these two equations we obtain a simple quadratic equation for G(z) that we

can immediately solve to obtain

G(z) =



z −

−



(9)

(From the definition of G(z) we see that G(z) → 1/z for large z and thus we choose the

negative root.) We immediately deduce that

ρ(E) =

πa

− E

(10)

where a

= 4/m

. This is a famous result known as Wigner’s semicircle law.

The Dyson gas

I hope that you are struck by the elegance of the large N planar diagram approach. But you

might have also noticed that the gluons do not interact. It is as if we have solved quantum

electrodynamics while we have to solve quantum chromodynamics. What if we have to

deal with V(ϕ)=

+ gϕ

? The gϕ

term causes the gluons to interact with each

other, generating horrible diagrams such as the one in figure VII.4.7. Clearly, diagrams

proliferate and as far as I know nobody has ever been able to calculate G(z) using the

Feynman diagram approach.

Happily, G(z) can be evaluated using another method known as the Dyson gas approach.

The key is to write

ϕ = U

†

U (11)

VII.4. Large N Expansion | 401

Figure VII.4.7

where  denotes the N by N diagonal matrix with diagonal elements equal to λ

, i =

1,...,N. Change the integration variable in (3) from ϕ to U and :

Z =







dλ



−N



V(λ

)

(12)

with J the Jacobian. Since the integrand does not depend on U we can throw away the

integral over U. It just gives the volume of the group SU(N ). Does this remind you of

chapter VII.1? Indeed, in (11) U corresponds to the unphysical gauge degrees of freedom—

the relevant degrees of freedom are the eigenvalues {λ

}. As an exercise you can use the

Faddeev-Popov method to calculate J .

Instead, we will follow the more elegant tack of determining J by arguing from general

principles. The change of integration variables in (11) is ill defined when any two of the λ

’s

are equal, at which point J must vanish. (Recall that the change from Cartesian coordinates

to spherical coordinates is ill defined at the north and south poles and indeed the Jacobian

in sin θdθdϕ vanishes at θ = 0 and π .) Since the λ

’s are created equal, interchange

symmetry dictates that J = [

m>n

(λ

− λ

)]

. The power β can be fixed by dimensional

analysis. With N

matrix elements dϕ obviously has dimension λ

while (

dλ

)J has

dimension λ

βN(N−1)/2

; thus β = 2.

Having determined J , let us rewrite (12) as

Z =



(

dλ

)[

m>n

(λ

− λ

)]

−N



V(λ

)



(

dλ

−N



V(λ



m=n

log(λ

−λ

)

(13)

Dyson pointed out that in this form Z =



(

dλ

−NE(λ

, ...,λ

)

is just the partition

function of a classical 1-dimensional gas (recall chapter V.2). Think of λ

, a real number,

as the position of the ith molecule. The energy of a configuration

E(λ

,...,λ

) =



V(λ

) −



m=n

log(λ

− λ

)

(14)

consists of two terms with obvious physical interpretations. The gas is confined in a

potential well V(x) and the molecules repel

each other with the two-body potential

−(1/N ) log(x − y)

. Note that the two terms in E are of the same order in N since each

Note that this corresponds to the repulsion between energy levels in quantum mechanics.