Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

362 | VI. Field Theory and Condensed Matter

over those h(



k, ω) with



k and ω larger than  − δ but smaller than . This is precisely

what we mean when we say that we don’t care about the fluctuations of h(x , t) on length

and time scales less than ( − δ)

−1

Putting on blurry glasses

For the sake of simplicity, let us go back to our favorite, the λϕ

theory, instead of the surface

growth problem. Recall from the preceding chapters the importance of the Euclidean λϕ

theory in modern condensed matter theory. So, continue the λϕ

theory to Euclidean space

and stare at the integral

Z() =





Dϕe

−



xL(ϕ)

(11)

The notation





instructs us to include only those field configurations ϕ(x) =



k/(2π)

ikx

ϕ(k) such that ϕ(k) = 0 for |k|≡(



i=1

)

larger than . As explained

in the text this amounts to putting on blurry glasses with resolution L = 1/:Wedonot

admit or see fluctuations with length scales less than L.

Evidently, the O(d) invariance, namely the Euclidean equivalent of Lorentz invariance,

will make our lives considerably easier. In contrast, for the surface growth problem we will

need special glasses that blur space and time differently.

We are now ready to make our glasses blurrier by letting  →  − δ (with δ > 0).

Write ϕ = ϕ

+ ϕ

(s for “smooth” and w for “wriggly”), defined such that the Fourier

components ϕ

(k) and ϕ

(k) are nonzero only for |k|≤( − δ) and ( − δ) ≤|k|≤

, respectively. (Obviously, the designation “smooth” and “wriggly” is for convenience.)

Plugging into (11) we can write

Z() =



−δ

Dϕ

−



xL(ϕ

)



Dϕ

−



(ϕ

, ϕ

)

(12)

where all the terms in L

(ϕ

, ϕ

) depend on ϕ

. (What we are doing here is somewhat

reminiscent of what we did in chapter IV.3.) Imagine doing the integral over ϕ

. Call the

result

−



xδL(ϕ

)

≡



Dϕ

−



(ϕ

, ϕ

)

and thus we have

Z() =



−δ

Dϕ

−



x[L(ϕ

)+δL(ϕ

)]

(13)

There, we have done it! We have rewritten the theory in terms of the “smooth” field ϕ

Of course, this is all formal, since in practice the integral over ϕ

can only be done

perturbatively assuming that the relevant couplings are small. If we could do the integral

In condensed matter physics, the so-called dynamical exponent z measures this difference. More precisely,

in the context of the surface growth problem, the correlator (introduced in chapter VI.6) satisfies the dynamic

scaling form given in (VI.6.3). Naively, the dynamical exponent z should be 2. (For a brief review of all this, see

M. Kardar and A. Zee, Nucl. Phys. B464[FS]: 449, 1996, cond-mat/9507112.)

VI.8. Renormalization Group Flow | 363

over ϕ

exactly, we might as well just do the integral over ϕ and then we would have no

need for all this renormalization group stuff.

For pedagogical purposes, consider more generally L =

(∂ϕ)



...

(so

that λ

is the usual

and λ

the usual λ.) Since terms such as ∂ϕ

∂ϕ

integrate to zero,

we have



(ϕ

, ϕ

) =





(∂ϕ

)

...



with ϕ

hiding in the (

...

). This describes a field ϕ

interacting with both itself and a

background field ϕ

(x). By symmetry considerations δL(ϕ

) has the same form as L(ϕ

)

but with different coefficients. Adding δL(ϕ

) to L(ϕ

) thus shifts

the couplings λ

[and the

coefficient of

(∂ϕ

)

.] These shifts generate the flow in the space of couplings I described

earlier.

We could have perfectly well left (13) as our end result. But suppose we want to compare

(13) with (11). Then we would like to change the



−δ

in (13) to





. For convenience,

introduce the real number b<1by − δ = b.In



−δ

we are told to integrate over

fields with |k|≤b. So all we have to do is make a trivial change of variable: Let k = bk



so that |k



|≤. But then correspondingly we have to change x =x



/b so that e

ikx



Plugging in, we obtain



xL(ϕ

) =





−d



(∂



)



...



(14)

where ∂



= ∂/∂x



= (1/b)∂/∂x. Define ϕ



by b

2−d

(∂



)

= (∂



)

or in other words ϕ



(2−d)

. Then (14) becomes







(∂



)



−d+(n/2)(d−2)

n

...



Thus, if we define the coefficient of ϕ

n

as λ



we have



= b

(n/2)(d−2)−d

(15)

an important result in renormalization group theory.

Relevant, irrelevant, and marginal

Let us absorb what this means. (For the time being, let us ignore δL(ϕ

) to keep the

discussion simple.) As we put on blurrier glasses, in other words, as we become interested

in physics over longer distance scales, we can once again write Z() as in (11) except that

the couplings λ

have to be replaced by λ



. Since b<1 we see from (15) that the λ

’s with

(n/2)(d − 2) − d>0 get smaller and smaller and can eventually be neglected. A dose of

jargon here: The corresponding operators ϕ

(for historical reasons we revert for an instant

Terms such as (∂ϕ)

can also be generated and that is why I wrote L(ϕ) with the (

...

) under which terms such

as these can be swept. You can check later that for most applications these terms are irrelevant in the technical

sense to be defined below.

364 | VI. Field Theory and Condensed Matter

from the functional integral language to the operator language) are called irrelevant. They

are the losers. Conversely, the winners, namely the ϕ

’s for which (n/2)(d − 2) − d<0,

are called relevant. Operators for which (n/2)(d − 2) − d =0 are called marginal.

For example, take n = 2:m

2

= b

−2

and the mass term is always relevant in any

dimension. On the other hand, take n = 4, and we see that λ



= b

d−4

λ and ϕ

is relevant

for d<4, irrelevant for d>4, and marginal at d =4. Similarly, λ



= b

2d−6

λ and ϕ

marginal at d = 3 and becomes irrelevant for d>3.

We also see that d =2 is special: All the ϕ

’s are relevant.

Now all this may ring a bell if you did the exercises religiously. In exercise III.2.1

you showed that the coupling λ

has mass dimension [λ

] = (n/2)(2 − d) + d . Thus, the

quantity (n/2)(d − 2) − d is just the length dimension of λ

. For example, for d = 4,

has mass dimension −2 and thus as explained in chapter III.2 the ϕ

interaction is

nonrenormalizable, namely that it has nasty behavior at high energy. But condensed matter

physicists are interested in the long distance limit, the opposite limit from the one that

interests particle physicsts. Thus, it is the nasty guys like ϕ

that become irrelevant in the

long distance limit.

One more piece of jargon: Given a scalar field theory, the dimension d at which the most

relevant interaction becomes marginal is known as the critical dimension in condensed

matter physics. For example, the critical dimension for a ϕ

theory is 3. It is now just

a matter of “high school arithmetic” to translate (15) into differential form. Write λ



+ δλ

; then from b = 1 − (δ/) we have δλ

=−[

(d − 2) − d]λ

(δ/).

Let us now be extra careful about signs. As I have already remarked, for (n/2)(d − 2) −

d>0 the coupling λ

(which, for definiteness, we will think of as positive) get smaller,

as is evident from (15). But since we are decreasing  to  − δ, a positive δ actually

corresponds to the resolution of our blurry glasses L = 

−1

changing to L + L(δ/).

Thus we obtain

dλ

=−



(d − 2) − d



, (16)

so that for (n/2)(d − 2) − d>0 a positive λ

would decrease as L increases.

In particular, for n = 4, L(dλ/dL) = (4 − d)λ. In most condensed matter physics appli-

cations, d ≤3 and so λ increases as the length scale of the physics under study increases.

The ϕ

coupling is relevant as noted above.

The δL(ϕ

), which we provisionally neglected, contributes an additional term, which we

call dynamical in contrast to the geometrical or “trivial” term displayed, to the right-hand

side of (16). Thus, in general L(dλ

/dL) =−[(n/2)(d −2) −d] λ

+K(d, n,

...

, λ

...

with the dynamical term K depending not only on d and n, but also on all the other

couplings. [For example, in (5) the “trivial” term vanishes since we are in 4-dimensional

spacetime; there is only a dynamical contribution.]

Note that what appears on the right-hand side is minus the length dimension of λ

, not the length dimension

(n/2)(d − 2) −d as one might have guessed naively.

VI.8. Renormalization Group Flow | 365

As you can see from this discussion, a more descriptive name for the renormalization

group might be “the trick of doing an integral a little bit at a time.”

Exploiting symmetry

To determine the renormalization group flow of the coupling g in the surface growth

problem we can repeat the same type of computation we did to determine the flow of the

coupling λ and of e in our two previous examples, namely we would calculate, to use the

language of particle physics, the amplitude for h-h scattering to one loop order. But instead,

let us follow the physical picture of Kadanoff et al. In Z() =



Dhe

−S(h)

we integrate over

only those h(



k, ω) with



k and ω larger than  − δ but less than .

I will now show you how to exploit the symmetry of the problem to minimize our labor.

The important thing is not necessarily to learn about the dynamics of surface growth,

but to learn the methodology that will serve you well in other situations. I have picked

a particularly “difficult” nonrelativistic problem whose symmetries are not manifest, so

that if you master the renormalization group for this problem you will be ready for almost

anything.

Imagine having done this partial integration and call the result



Dhe

−

S(h)

. At this point

you should work out the symmetries of the problem as indicated in the exercises. Then

you can argue that

S(h) must have the form

S(h) =



xdt



∂

∂t

− β∇



h − α

(∇h)



...

, (17)

depending on two parameters α and β. The (

...

) indicates terms involving higher powers

of h and its derivatives. The simplifying observation is that the same coefficient α multiplies

both ∂h/∂t and (g/2)(∇h)

. Once we know α and β then by suitable rescaling we can

bring the action

S(h) back into the same form as S(h) and thus find out how g changes.

Therefore, it suffices to look at the (∂h/∂t)

and (∇

terms in the action, or equivalently

at the propagator, which is considerably simpler to calculate. As Rudolf Peierls once said

to the young Hans Bethe, “Erst kommt das Denken, dann das Integral.” (Roughly, “First

think, then do the integral.”) We will not do the computation here. Suffice it to note that g

has the high school dimension of (length)

(D−2)

(see exercise VI.8.5). Thus, according to

the preceding discussion we should have

(2 − D)g + c

...

(18)

A detailed calculation is needed to determine the coefficient c

, which obviously

depends on the dimension of space D since the Feynman integrals depend on D.

The equation tells us how g, an effective measure of nonlinearity in the physics of

John Wheeler gave me similar advice when I was a student: “Never calculate without first knowing the

answer.”

366 | VI. Field Theory and Condensed Matter

surface growth, changes when we change the length scale L. For the record, c

[S(D)/4(2π)

](2D − 3)/D, with S(D) the D-dimensional solid angle. The interesting

factor is of course (2D − 3), changing sign between

D = 1 and 2.

Localization

As I said earlier, renormalization group flow has literally become part of the language of

condensed matter and high energy physics. Let me give you another example of the power

of the renormalization group. Go back to Anderson localization (chapter VI.7), which so

astonished the community at the time. People were surprised that the localization behavior

depends so drastically on the dimension of space D, and perhaps even more so, that for

D = 2 all states are localized no matter how weak the strength of the disorder. Our usual

physical intuition would say that there is a critical strength. As we will now see, both

features are quite naturally accounted for in the renormalization group language. Already,

you see in (18) that D enters in an essential way.

I now offer you a heuristic but beautiful (at least to me) argument given by Abra-

hams, Anderson, Licciardello, and Ramakrishnan, who as a result became known to the

condensed matter community as the “Gang of Four.” First, you have to understand the

difference between conductivity σ and conductance G in solid state physics lingo. Conduc-

tivity

is defined by



J = σ



E, where



J measures the number of electrons passing through

a unit area per unit time. Conductance G is the inverse of resistance (the mnemonic: the

two words rhyme). Resistance R is the property of a lump of material and defined in high

school physics by V = IR, where the current I measures the number of electrons passing

by per unit time. To relate σ and G, consider a lump of material, taken to be a cube of size

L, with a voltage drop V across it. Then I = JL

=σEL

=σ (V /L)L

=σLV and thus

G(L) = 1/R = I/V = σL. Next, let us go to two dimensions. Consider a thin sheet of ma-

terial of length and width L and thickness a  L. (We are doing real high school physics,

not talking about some sophisticated field theorist’s idea of two dimensional space!) Again,

apply a voltage drop V over the length L : I =J(aL)= σEaL= σ (V /L)aL =σVa and so

G(L) = 1/R = I/V = σa. I will let you go on to one dimension: Consider a wire of length

L and width and thickness a. In this way, we obtain G(L) ∝ L

D−2

. Incidentally, condensed

matter physicists customarily define a dimensionless conductance g(L) ≡ G(L)/e

Incidentally, the theory is exactly solvable for D = 1 (with methods not discussed in this book).

Over the years I have asked a number of high energy theorists how is it possible to obtain



J = σ



E, which

manifestly violates time reversal invariance, if the microscopic physics of an electron scattering on an impurity

atom perfectly well respects time reversal invariance. Very few knew the answer. The resolution of this apparent

paradox is in the order of limits! Condensed matter theorists calculate a frequency and wave vector dependent

conductivity σ(ω,



k) and then take the limit ω,



k → 0 and



/ω → 0. Before the limit is taken, time reversal

invariance holds. The time it takes the particle to find out that it is in a box of size of order 1/k is of order 1/(Dk

)

(with D the diffusion constant). The physics is that this time has to be much longer than the observation time

∼ 1/ω.

Sam Treiman told me that when he joined the U.S. Army as a radio operator he was taught that there were

three forms of Ohm’s law: V =IR, I = V/R, and R = V/I. In the second equality here we use the fourth form.

VI.8. Renormalization Group Flow | 367

−1

β(g)

D = 3

D = 2

D = 1

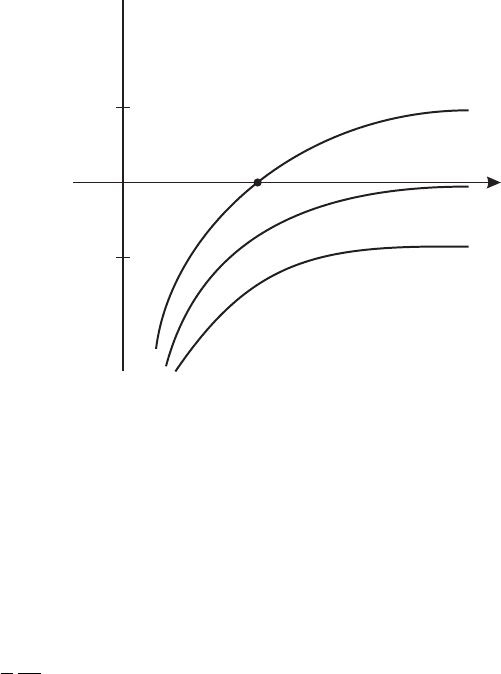
Figure VI.8.2

We also know the behavior of g(L) when g(L) is small or, in other words, when the

material is an insulator for which we expect g(L) ∼ ce

−L/ξ

, with ξ some length charac-

teristic of the material and determined by the microscopic physics. Thus, for g(L) small,

L(dg/dL) =−(L/ξ )g(L) = g(L)[log g(L) − log c], where the constant log c is negligible

in the regime under consideration.

Putting things together, we obtain

β(g) ≡



(D − 2) +

...

for large g

log g +

...

for small g

(19)

First, a trivial note: in different subjects, people define β(g) differently (without affecting

the physics of course). In localization theory, β(g)is traditionally defined as d log g/d log L

as indicated here. Given (19) we can now make a “most plausible” plot of β(g) as shown

in figure VI.8.2. You see that for D = 2 (and D = 1) the conductance g(L) always flows

toward 0 as we go to long distances (macroscopic measurements on macroscopic materials)

regardless of where we start. In contrast, for D =3, if g

the initial value of g is greater than

a critical g

then g(L) flows to infinity (presumably cut off by physics we haven’t included)

and the material is a metal, while if g

, the material is an insulator. Incidentally,

condensed matter theorists often speak of a critical dimension D

at which the long

distance behavior of a system changes drastically; in this case D

= 2.

Effective description

In a sense, the renormalization group goes back to a basic notion of physics, that the

effective description can and should change as we move from one length scale to another.

For example, in hydrodynamics we do not have to keep track of the detailed interaction

368 | VI. Field Theory and Condensed Matter

among water molecules. Similarly, when we apply the renormalization group flow to the

strong interaction, starting at high energies and moving toward low energies, the effective

description goes from a theory of quarks and gluons to a theory of nucleons and mesons.

In this more general picture then, we no longer think of flowing in a space of coupling

constants, but in “the space of Hamiltonians” that some condensed matter physicists like

to talk about.

Exercises

VI.8.1 Show that the solution of dg/dt =−bg

...

is given by

α(t)

α(0)

+ 8πbt +

...

(20)

where we defined α(t) = g(t)

/4π .

VI.8.2 In our discussion of the renormalization group, in λϕ

theory or in QED, for the sake of simplicity

we assumed that the mass m of the particle is much smaller than μ and thus set m equal to zero. But

nothing in the renormalization group idea tells us that we can’t flow to a mass scale below m. Indeed, in

particle physics many orders of magnitude separate the top quark mass m

from the up quark mass m

We might want to study how the strong interaction coupling flows from some mass scale far above m

down to some mass scale μ below m

but still large compared to m

. As a crude approximation, people

often set any mass m below μ equal to zero and any m above μ to infinity (i.e., not contributing to the

renormalization group flow). In reality, as μ approaches m from above the particle starts to contribute

less and drops out as μ becomes much less than m. Taking either the λϕ

theory or QED study this

so-called threshold effect.

VI.8.3 Show that (10) is invariant under the so-called Galilean transformation

h(x, t) → h



(x, t) = h



x +g ut , t



+u

x +

t (21)

Show that because of this symmetry only two parameters α and β appear in (17).

VI.8.4 In

S(h) only derivatives of the field h can appear and not the field itself. (Since the transformation

h(x , t) →h(x , t) +c with c a constant corresponds to a trivial shift of where we measure the surface

height from, the physics must be invariant under this transformation.) Terms involving only one power

of h cannot appear since they are all total divergences. Thus,

S(h) must start with terms quadratic in h.

Verify that the

S(h) given in (17) is indeed the most general. A term proportional to (∇h)

is also allowed

by symmetries and is in fact generated. However, such a term can be eliminated by transforming to a

moving coordinate frame h → h + ct.

VI.8.5 Show that g has the high school dimension of (length)

(D−2)

. [Hint: The form of S(h) implies that t has

the dimension of length squared and so h has the dimension (length)

(2−D)

.] Comparing the terms ∇

and g(∇h)

we determine the dimension of g.]

VI.8.6 Calculate the h propagator to one loop order. Extract the coefficients of the ω

and k

terms in a low

frequency and wave number expansion of the inverse propagator and determine α and β.

VI.8.7 Study the renormalization group flow of g for D = 1, 2, 3.

Part VII Grand Unification

This page intentionally left blank

VII.1

Quantizing Yang-Mills Theory

and Lattice Gauge Theory

One reason that Yang-Mills theory was not immediately taken up by physicists is that

people did not know how to calculate with it. At the very least, we should be able to

write down the Feynman rules and calculate perturbatively. Feynman himself took up the

challenge and concluded, after looking at various diagrams, that extra fields with ghostlike

properties had to be introduced for the theory to be consistent. Nowadays we know how

to derive this result more systematically.

The story goes that Feynman wanted to quantize gravity but Gell-Mann suggested to

him to first quantize Yang-Mills theory as a warm-up exercise.

Consider pure Yang-Mills theory—it will be easy to add matter fields later. Follow what

we have learned. Split the Lagrangian L = L

as usual into two pieces (we also choose

to scale A → gA):

=−

(∂

− ∂

)

(1)

and

=−

g(∂

− ∂

abc

bμ

cν

−

abc

ade

dμ

eν

(2)

Then invert the differential operator in the quadratic piece (1) to obtain the propagator.

This part looks the same as the corresponding procedure for quantum electrodynamics,

except for the occurrence of the index a. Just as in electrodynamics, the inverse does not

exist and we have to fix a gauge.

I built up the elaborate Faddeev-Popov method to quantize quantum electrodynamics

and as I noted, it was a bit of overkill in that context. But here comes the payoff: We can now

turn the crank. Recall from chapter III.4 that the Faddeev-Popov method would give us

Z =



DAe

iS(A)

(A)δ[f (A)] (3)

with (A) ≡{



Dgδ[f(A

)]}

−1

and S(A) =



xL the Yang-Mills action. (As in chap-

ter III.4, A

≡gAg

−1

−i(∂g)g

−1

denotes the gauge transform of A. Here g ≡g(x) denotes