Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

382 | VII. Grand Unification

The theory works itself out

Now that the couplings of the gauge bosons to the various fields, in particular, the Higgs

field, are determined, we can easily work out the mass spectrum of the gauge bosons, as

indeed, let me remind you, you have already done in exercise IV.6.3!

Upon spontaneous symmetry breaking ϕ → (1/

√





(the normalization is conven-

tional): We simply plug in

L = (D

ϕ)

†

ϕ) →

−μ

(gW

− g



)

(4)

I trust that this is what you got! Thus, the linear combination gW

−g



becomes massive

while the orthogonal combination remains massless and is identified with the photon. It

is clearly convenient to define the angle θ by tan θ =g



/g. Then,

= cos θW

− sin θB

(5)

describes a massive gauge boson known as the Z boson, while the electromagnetic po-

tential is given by A

= sin θW

+ cos θB

. Combine (4) and (5) and verify that the mass

squared of the Z boson is M

= v

+ g

2

)/4, and thus by elementary trigonometry ob-

tain the relation

= M

cos θ (6)

The exchange of the W boson generates the Fermi weak interaction

L =−

¯ν

¯e

=−

√

¯ν

¯e

where the second equality merely gives the historical definition of the Fermi coupling G.

Thus,

√

(7)

Next, we write the relevant piece of the covariant derivative

+ g



= g(cos θZ

+ sin θA

+ g



(− sin θZ

+ cos θA

)

in terms of the physically observed Z and A. The coefficient of A

works out to be

g sin θT

+ g



cos θ(Y/2) = g sin θ(T

+ Y/2); the fact that the combination Q = T

Y/2 emerges provides a nice check on the formalism. Furthermore, we obtain

e = g sin θ (8)

Meanwhile, it is convenient to write g cos θT

− g



sin θ(Y/2), the coefficient of Z

the covariant derivative, in terms of the physically familiar electric charge Q rather than

the theoretical hypercharge Y : Thus,

g cos θT

− g



sin θ(Q − T

) =

cos θ

− sin

θQ)

VII.2. Electroweak Unification | 383

In other words, we have determined the coupling of the Z boson to an arbitrary fermion

field  in the theory:

L =

cos θ

γ

− sin

θQ) (9)

For example, using (9) we can immediately write the coupling of Z to leptons:

L =

cos θ

[

(¯ν

−¯e

) + sin

θ ¯eγ

e] (10)

Including quarks

How to include the hadrons is now almost self evident. Given that only left handed

fields participate in the weak interaction, we put the quarks of the first generation into

SU(2) ⊗ U(1) multiplets as follows:

≡





, u

, d

(11)

where α = 1, 2, 3 denotes the color index, which I will discuss in the next chapter. The

right handed quarks u

and d

are put into singlets so that they do not hear the weak

bosons W

. Recall that the up quark u and the down quark d have electric charges

and

−

respectively. Referring to (3) we see

Y =

, and −

for q

, u

, and d

, respectively.

From (9) we can immediately read off the coupling of the Z boson to the quarks:

L =

cos θ

[

( ¯u

−

) − sin

θJ

] (12)

Finally, I leave it to you to verify that of the four degrees of freedom contained in ϕ

(since ϕ

and ϕ

are complex) three are eaten by the W and Z bosons, leaving one physical

degree of freedom H corresponding to the elusive Higgs particle that experimenters are

still searching for as of this writing.

The neutral current

By virtue of its elegantly economical gauge group structure, this SU(2) ⊗U(1) electroweak

theory of Glashow, Salam, and Weinberg ushered in the last great predictive era of theo-

retical particle physics. Writing (10) and (12) as

L =

cos θ

leptons

+ J

quarks

)

and using (6) we see that Z boson exchange generates a hitherto unknown neutral current

interaction

neutral current

=−

leptons

+ J

quarks

)

leptons

+ J

quarks

)

between leptons and quarks. By studying various processes described by L

neutral current

can determine the weak angle θ . Once θ is determined, we can predict g from (8). Once g

384 | VII. Grand Unification

is determined, we can predict M

from (7). Once M

is determined, we can predict M

from (6).

Concluding remarks

As I mentioned, there are three families of leptons and quarks in Nature, consisting

of (ν

, e, u, d), (ν

, μ, c, s), and (ν

, τ , t , b). The appearance of this repetitive family

structure, about which the SU(2) ⊗ U(1) theory has nothing to say, represents one of

the great unsolved puzzles of particle physics. The three families, with the appropriate

rotation angles between them, are simply incorporated into the theory by repeating what

we wrote above.

A more logical approach than the one given here would be to start with an SU(2) ⊗U(1)

theory with a doublet Higgs field with some hypercharge, and to say, “Behold, upon

spontaneous symmetry breaking, one linear combination of generators remains unbroken

with a corresponding massless gauge field.” I think that our quasi-historical approach is

clearer.

As I have mentioned on several occasions, Fermi’s theory of the weak interaction is

nonrenormalizable. In 1999, ’t Hooft and Veltman were awarded the Nobel Prize for

showing that the SU(2) ⊗U(1) electroweak theory is renormalizable, thus paving the way

for the triumph of nonabelian gauge theories in describing the strong, electromagnetic,

and weak interactions. I cannot go into the details of their proof here, but I would like

to mention that the key is to start with the nonabelian analog of the unitary gauge (recall

chapter IV.6) and proceed to the R

gauge. At large momenta, the massive gauge boson

propagators go as ∼ (k

) in the unitary gauge, but as ∼ (1/k

) in the R

gauge. The

theory is then renormalizable by power counting.

Exercises

VII.2.1 Unfortunately, the mass of the elusive Higgs particle H depends on the parameters in the double well

potential V =−μ

†

ϕ + λ(ϕ

†

ϕ)

responsible for the spontaneous symmetry breaking. Assuming that

H is massive enough to decay into W

−

and Z + Z, determine the rates for H to decay into various

modes.

VII.2.2 Show that it is possible to stay with the SU(2) gauge group and to identify W

as the photon A, but at

the cost of inventing some experimentally unobserved lepton fields. This theory does not describe our

world: For one thing, it is essentially impossible to incorporate the quarks. Show this! [Hint: We have to

put the leptons into a triplet of SU(2) instead of a doublet.]

VII.3 Quantum Chromodynamics

Quarks

Quarks come in six flavors, known as up, down, strange, charm, bottom, and top, denoted

by u, d , s , c, b, and t. The proton, for example, is made of two up quarks and a down quark

∼ (uud), while the neutral pion corresponds to ∼ (u ¯u − d

d)/

√

2. Please consult any text

on particle physics for details.

By the late 1960s the notion of quarks was gaining wide acceptance, but two separate

lines of evidence indicated that a crucial element was missing. In studying how hadrons

are made of quarks, people realized that the wave function of the quarks in a nucleon does

not come out to be antisymmetric under the interchange of any pair of quarks, as required

by the Pauli exclusion principle. At around the same time, it was realized that in the ideal

world we used to derive the Goldberger-Treiman relation and in which the pion is massless

we can calculate the decay rate for the process π

→γ + γ , as mentioned in chapter IV.7.

Puzzlingly enough, the calculated rate came out smaller than the observed rate by a factor

of 9 = 3

Both puzzles could be resolved in one stroke by having quarks carry a hitherto unknown

internal degree of freedom that Gell-Mann called color. For any specified flavor, a quark

comes in one of three colors. Thus, the up quark can be red, blue, or yellow. In a nucleon,

the wave function of the three quarks will then contain a factor referring to color, besides

the factors referring to orbital motion, spin, and so on. We merely have to make the color

part of the wave function antisymmetric; in fact, we simply take it to be ε

αβγ

, where α, β ,

and γ denote the colors carried by the three quarks. With quarks in three colors, we have to

multiply the amplitude for π

decay by a factor of 3, thus neatly resolving the discrepancy

between theory and experiment.

386 | VII. Grand Unification

Asymptotic freedom

As I mentioned in chapter VI.6, the essential clue came from studying deep inelastic scat-

tering of electrons off nucleons. Experimentalists made the intriguing discovery that when

hit hard the quarks in the nucleons act as if they hardly interact with each other, in other

words, as if they are free. On the other hand, since quarks are never seen as isolated enti-

ties, they appear to be tightly bound to each other within the nucleon. As I have explained,

this puzzling and apparently contradictory behavior of the quarks can be understood if the

strong interaction coupling flows to zero in the large momentum (ultraviolet) limit and to

infinity or at least to some large value in the small momentum (infrared) limit. A number

of theorists proposed searching for theories whose couplings would flow to zero in the

ultraviolet limit, now known as asymptotic free theories. Eventually, Gross, Wilczek, and

Politzer discovered that Yang-Mills theory is asymptotically free.

This result dovetails perfectly with the realization that quarks carry color. The nonabelian

gauge transformation would take a quark of one color into a quark of another color. Thus, to

write down the theory of the strong interaction we simply take the result of exercise IV.5.6,

L =−

μν

aμν

+¯q(iγ

− m)q (1)

with the covariant derivative D

=∂

−iA

. The gauge group is SU(3) with the quark field

q in the fundamental representation. In other words, the gauge fields A

= A

, where

(a = 1,...,8) are traceless hermitean 3 by 3 matrices. Explicitly, (A

)

where α, β =1, 2, 3. The theory is known as quantum chromodynamics, or QCD for short,

and the nonabelian gauge bosons are known as gluons. To incorporate flavor, we simply

write



j=1

¯q

(iγ

−m

for the second term in (1), where the index j goes over the

f flavors. Note that quarks of different flavors have different masses.

Infrared slavery

The flip side of asymptotic freedom is infrared slavery. We cannot follow the renormaliza-

tion group flow all the way down to the low momentum scale characteristic of the quarks

bound inside hadrons since the coupling g becomes ever stronger and our perturbative cal-

culation of β(g) is no longer adequate. Nevertheless, it is plausible although never proven

that g goes to infinity and that the gluons keep the quarks and themselves in permanent

confinement. The Wilson loop introduced in chapter VII.1 provides the order parameter

for confinement.

In elementary physics forces decrease with the separation between interacting objects,

so permanent confinement is a rather bizarre concept. Are there any other instances of

permanent confinement?

Consider a magnetic monopole in a superconductor. We get to combine what we learned

in chapters IV.4 and V.4 (and even VI.2)! A quantized amount of magnetic flux comes out

of the monopole, but according to the Meissner effect a superconductor expels magnetic

flux. Thus, a single magnetic monopole cannot live inside a superconductor.

VII.3. Quantum Chromodynamics | 387

M M

Figure VII.3.1

Now consider an antimonopole a distance R away (figure VII.3.1). The magnetic flux

coming out of the monopole can go into the antimonopole, forming a tube connecting

the monopole and the antimonopole and obliging the superconductor to give up being a

superconductor in the region of the flux tube. In the language of chapter V.4, it is no longer

energetically favorable for the field or order parameter ϕ to be constant everywhere; instead

it vanishes in the region of the flux tube. The energy cost of this arrangement evidently

grows as R (consistent with Wilson’s area law).

In other words, an experimentalist living inside a superconductor would find that

it costs more and more energy to pull a monopole and an antimonopole apart. This

confinement of monopoles inside a superconductor is often taken to be a model of the yet-

to-be-proven confinement of quarks. Invoking electromagnetic duality we can imagine

a magnetic superconductor in contrast to the usual electric superconductor. Inside a

magnetic superconductor, electric charges would be permanently confined. Our universe

may be likened to a color magnetic superconductor in which quarks (the analog of electric

charges) are confined.

On distance scales large compared to the radius of the color flux tube connecting a quark

to an antiquark, the tube can be thought of as a string. Historically, that was how string

theory originated. The challenge, boys and girls, is to prove that the ground state or vacuum

of (1) is a color magnetic superconductor.

Symmetries of the strong interaction

Now that we have a theory of the strong interaction, we can understand the origin of the

symmetries of the strong interaction, namely the isospin symmetry of Heisenberg and the

chiral symmetry that when spontaneously broken leads to the appearance of the pion as a

Nambu-Goldstone boson (as discussed in chapters IV.2 and VI.4).

Consider a world with two flavors, which is all that is relevant for a discussion of the pion.

Introduce the notation u ≡ q

, d ≡ q

, and q =





so that we can write the Lagrangian as

L =−

μν

aμν

+¯q(iγ

− m)q

with

m =



0 m



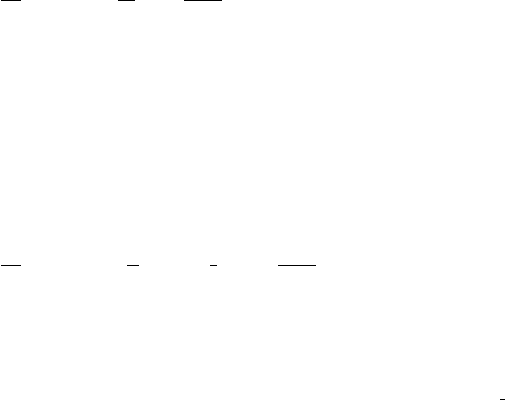
388 | VII. Grand Unification

where m

and m

are the masses of the up and down quarks, respectively. If m

= m

the Lagrangian is invariant under q → e

iθ

q, corresponding to Heisenberg’s isospin

symmetry.

In the limit in which m

and m

vanish, the Lagrangian is invariant under q → e

iϕ

τγ

q ,

known as the chiral SU(2) symmetry, chiral because the right handed quarks q

and the

left handed quarks q

transform differently. To the extent that m

and m

are both much

smaller than the energy scale of the strong interaction, chiral SU(2) is an approximate

symmetry.

The pion is the Nambu-Goldstone boson associated with the spontaneous breaking

of the chiral SU(2). Indeed, this is an example of dynamical symmetry breaking since

there is no elementary scalar field around to acquire a vacuum expectation. Instead, the

strong interaction dynamics is supposed to drive the composite scalar fields ¯uu and

dd to

“condense into the vacuum” so that 0|¯uu |0=0|

dd |0become nonvanishing, where the

equality between the two vacuum expectation values ensures that Heisenberg’s isospin is

not spontaneously broken, an experimental fact since there are no corresponding Nambu-

Goldstone bosons. In terms of the doublet field q, the QCD vacuum is supposed to be such

that 0|¯qq |0 = 0 while 0|¯q τq |0=0.

Renormalization group flow

The renormalization group flow of the QCD coupling is governed by

= β(g) =−

(G)

16π

(2)

with the all-crucial minus sign. Here

(G)δ

= f

acd

bcd

(3)

I will not go through the calculation of β(g) here, but having mastered chapters VI.8

and VII.1 you should feel that you can do it if you want to.

At the very least, you should

understand the factor g

and T

(G) by drawing the relevant Feynman diagrams.

When fermions are included,

= β(g) =

−

(G) +

(F )

16π

(4)

where

(F )δ

= tr[T

(F )T

(F )] (5)

I do expect you to derive (4) given (2). For SU(N) T

(F ) =

for each fermion in the

fundamental representation. Note that asymptotic freedom is lost when there are too many

fermions.

For a detailed calculation, see, e.g., S. Weinberg, The Quantum Theory of Fields, Vol. 2, sec. 18.7.

VII.3. Quantum Chromodynamics | 389

–

Figure VII.3.2

You already solved an equation like (4) in exercise VI.8.1. Let us define, in analogy to

quantum electrodynamics, α

(μ) ≡ g(μ)

/4π , the strong coupling at the momentum scale

μ. From (4) we obtain

(Q) =

(μ)

1 + (1/4π)(11 −

)α

(μ) log(Q

/μ

)

(6)

showing explicitly that α

(Q) → 0 logarithmically as Q →∞.

Electron-positron annihilation

I have space to show you only one physical application. Experimentalists have measured

the cross section σ of e

−

annihilation into hadrons as a function of the total center-of-

mass energy E. The amplitude is shown in figure VII.3.2. To calculate the cross section in

terms of the amplitude, we have to go through what some people call “boring kinematics,”

such as normalizing everything correctly, dividing by the flux of the two beams, and so

forth (see the appendix to chapter II.6). For the good of your soul, you should certainly go

through this type of calculation at least once. Believe me, I did it more times than I care

to remember. But happily, as I will now show you, we can avoid most of this grunge labor.

First, consider the ratio

R(E) ≡

σ(e

−

→ hadrons)

σ(e

−

→ μ

−

)

The kinematic stuff cancels out. In figure VII.3.2 the half of the diagram involving the

electron positron lines and the photon propagator also appears in the Feynman diagram

−

→μ

−

(figure VII.3.3) and so cancels out in R(E). The blob in figure VII.3.2, which

hides all the complexity of the strong interaction, is given by 0|J

(0) |h, where J

is the

For the accumulated experimental evidence on α

(Q), see figure 14.3 in F. Wilczek, in: V. Fitch et al., eds.,

Critical Problems in Physics, p. 281.

390 | VII. Grand Unification

−

Figure VII.3.3

electromagnetic current and the state |h can contain any number of hadrons. To obtain

the cross section we have to square the amplitude, include a δ-function for momentum

conservation, and sum over all |h, thus arriving at



(2π)

− p

−

)0|J

(0) |hh|J

(0) |0 (7)

[with q ≡ p

+ p

−

= (E ,



0)]. This quantity can be written as



iqx

0|J

(x)J

(0) |0=



iqx

0|[J

(x), J

(0)]|0

= 2Im(i



iqx

0|TJ

(x)J

(0) |0)

(The first equality follows from E>0 and the second was explained in chapter III.8.)

To determine this quantity, we would have to calculate an infinite number of Feynman

diagrams involving lots of quarks and gluons. A typical diagram is shown in figure VII.3.4.

Completely hopeless!

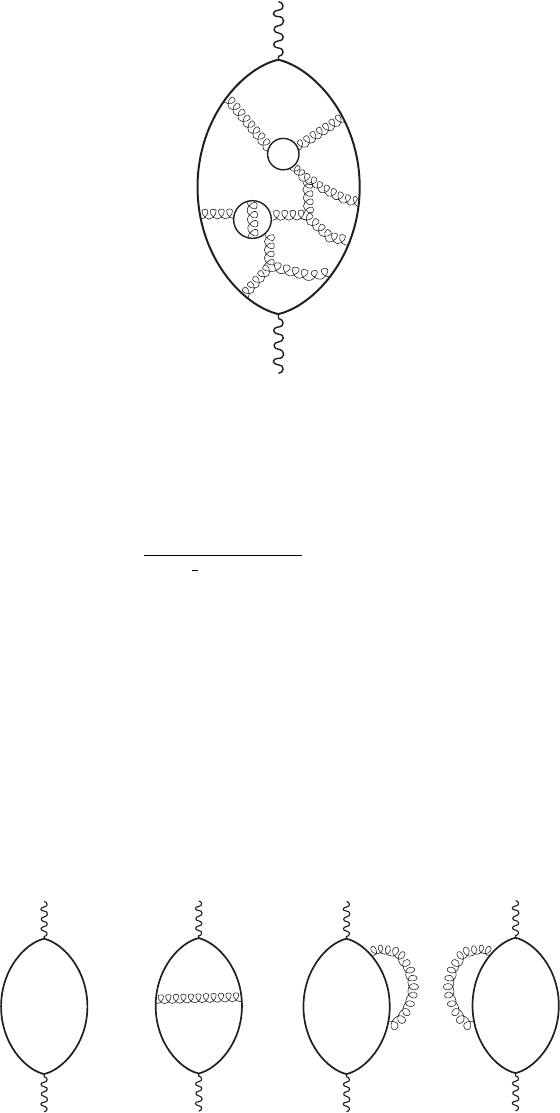
This is where asymptotic freedom rides to the rescue! From chapter VI.7 you learned

that for a process at energy E the appropriate coupling strength to use is g(E). But as we

crank up E, g(E) gets smaller and smaller. Thus diagrams such as figure VII.3.4 involving

many powers of g(E) all fall away, leaving us with the diagrams with no power of g(E)

(fig. VII.3.5a) and two powers of g(E) (figs. VII.3.5b,c,d). No calculation is necessary to

obtain the leading term in R(E), since the diagram in figure VII.3.5a is the same one

that enters into e

−

→ μ

−

: We merely replace the quark propagator by the muon

propagator (quark and muon masses are negligible compared to E). At high energy, the

quarks are free and R(E) merely counts the square of the charge Q

of the various quarks

contributing at that energy. We predict

R(E) −→

E→∞



(8)

The factor of 3 accounts for color.

VII.3. Quantum Chromodynamics | 391

Figure VII.3.4

Not only does QCD turn itself off at high energies, it tells us how fast it is turning itself

off. Thus, we can determine how the limit in (8) is approached:

R(E) =







1 + C

(11 −

) log(E/μ)

...



(9)

I will leave it to you to calculate C.

Dreams of exact solubility

An analytic solution of quantum chromodynamics is something of a “Holy Grail” for

field theorists (a grail that now carries a prize of one million dollars: see www.ams.org/

claymath/). Many field theorists have dreamed that at least “pure” QCD, that is QCD

without quarks, might be exactly soluble. After all, if any 4-dimensional quantum field

(a) (b) (c) (d)

Figure VII.3.5