Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

412 | VII. Grand Unification

This remarkable cancellation between sums of cubes of a strange list of numbers

suggests strongly, to say the least, that SU(5) is not the end of the story. Besides, it would

be nice if the 5

∗

and 10 could be unified into a single representation.

Exercises

VII.5.1 Write down the charge operator Q acting on 5, the defining representation ψ

. Work out the charge

content of the 10 = ψ

μν

and identify the various fields contained therein.

VII.5.2 Show that for any grand unified theory, as long as it is based on a simple group, we have at the unification

scale

sin

θ =



(18)

where the sum is taken over all fermions.

VII.5.3 Check that the SU(3) ⊗ SU(2) ⊗ U(1) theory is anomaly-free. [Hint: The calculation is more involved

than in SU(5) since there are more independent generators. First show that you only have to evaluate

tr Y {T

, T

} and tr Y

, with T

and Y the generators of SU(2) and U(1), respectively.]

VII.5.4 Construct grand unified theories based on SU(6), SU(7), SU(8), . . . , until you get tired of the game.

People used to get tenure doing this. [Hint: You would have to invent fermions yet to be experimentally

discovered.]

VII.6 Protons Are Not Forever

Proton decay

Charge conservation guarantees the stability of the electron, but what about the stability of

the proton? Charge conservation allows p → π

. No fundamental principle says that

the proton lives forever, but yet the proton is known for its longevity: It has been around

essentially since the universe began.

The stability of the proton had to be decreed by an authority figure: Eugene Wigner was

the first to proclaim the law of baryon number conservation. The story goes that when

Wigner was asked how he knew that the proton lives forever he quipped, “I can feel it in

my bones.” I take the remark to mean that just from the fact that we do not glow in the

dark we can set a fairly good lower bound on the proton’s life span.

As soon as we start grand unifying, we better start worrying. Generically, when we grand

unify we put quarks and leptons into the same representation of some gauge group [see

(VII.5.11 and VII.5.12)]. This miscegenation immediately implies that there are gauge

bosons transforming quarks into leptons and vice versa. The bag of three quarks known

as the proton could very well get turned into leptons upon the exchange of these gauge

bosons. In other words, the proton, the rock on which our world is built upon, may not be

forever! Thus, grand unification runs the risk of being immediately falsified.

Let M

denote generically the masses of those gauge bosons transforming quarks into

leptons and vice versa. Then the amplitude for proton decay is of order g

, with g

the coupling strength of the grand unifying gauge group, and the proton decay rate  is

given by (g

)

times a phase space factor controlled essentially by the proton mass

since the pion and positron masses are negligible compared to the proton mass. By

dimensional analysis, we determine that  ∼ (g

)

. Since the proton is known to

live for something like at least 10

years, M

had better be huge compared to the kind of

energy scales we can reach experimentally.

The mass M

is of the same order as the mass scale M

GUT

at which the grand unified

theory is spontaneously broken down to SU(3) ⊗SU(2) ⊗ U(1). Specifically, in the SU(5)

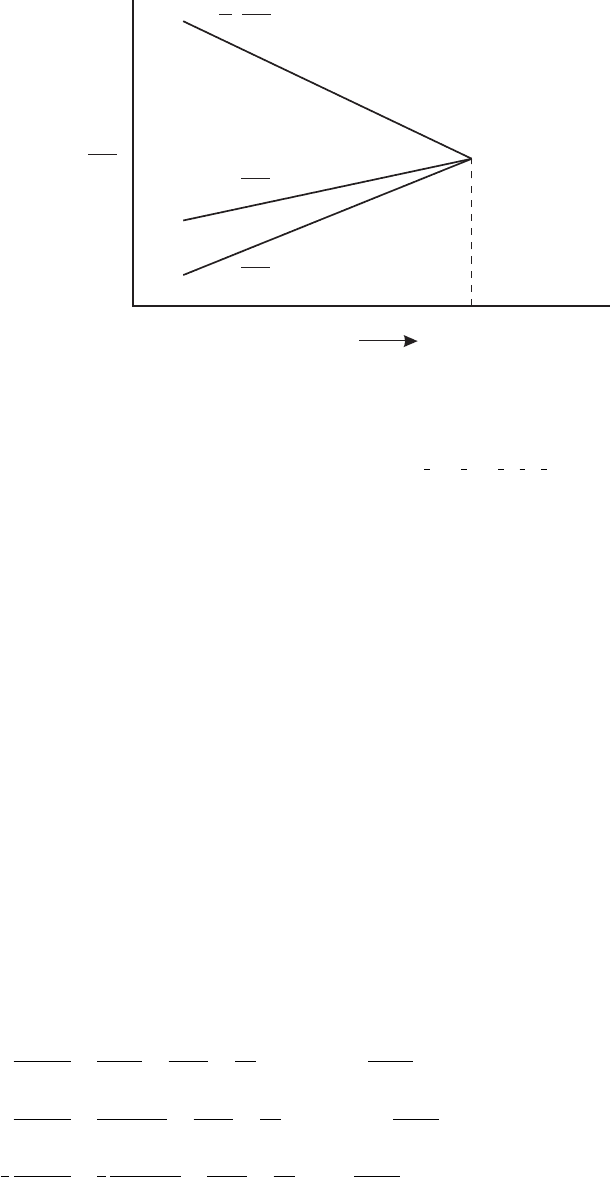
414 | VII. Grand Unification

( )

4π

GUT

Figure VII.6.1

theory, a Higgs field H

transforming as the adjoint 24, with its vacuum expectation value

H

 equal to the diagonal matrix with elements (−

, −

) times some v, can

do the job, as was discussed in chapter IV.6. The gauge bosons in SU(3) ⊗ SU(2) ⊗ U(1)

remain massless while the other gauge bosons acquire mass M

of order gv.

To determine M

GUT

, we apply renormalization group flow to g

, g

, and g

, the cou-

plings of SU(3), SU(2), and U(1), respectively. The idea is that as we move up in the

mass or energy scale μ the two asymptotically free couplings g

(μ) and g

(μ) decrease

while g

(μ) increases. Thus, at some mass scale M

GUT

they will meet and that is where

SU(3) ⊗ SU(2) ⊗U(1) is unified into SU(5) (see figure VII.6.1). Because of the extremely

slow logarithmic running (it should be called walking or even crawling but again for his-

torical reasons we are stuck with running) of the coupling constant, we anticipate that the

unification mass scale M

GUT

will come out to be much larger than any scale we were used

to in particle physics prior to grand unification. In fact, M

GUT

will turn out to have an

enormous value of the order 10

14−15

Gev and the idea of grand unification passes its first

hurdle.

Stability of the world implies the weakness of electromagnetism

Using the result of exercise VI.8.1 we obtain (here α

≡ g

/4π and α

GUT

≡ g

/4π denote

the strong interaction and grand unification analog of the fine structure constant α,

respectively, with F the number of families)

4π

(μ)]

≡

(μ)

GUT

6π

(4F −33) log

GUT

(1)

4π

(μ)]

≡

sin

θ(μ)

α(μ)

GUT

6π

(4F −22) log

GUT

(2)

4π

(μ)]

≡

cos

θ(μ)

α(μ)

GUT

6π

4F log

GUT

(3)

VII.6. Protons Are Not Forever | 415

By θ(μ) we mean the value of θ at the scale μ.Atμ = M

GUT

, the three couplings are related

through SU(5).

We evaluate these equations for some experimentally accessible value of μ, plugging in

measured values of α

and α. With three equations, we not only manage to determine the

unification scale M

GUT

and coupling α

GUT

, but we can predict θ . In other words, unless

the ratio g

to g

is precisely right, the three lines in figure VII.6.1 will not meet at one

point.

Note that the number of fermion families F contributes equally to (1), (2), and (3). This is

as it should be since the fermions are effectively massless for the purpose of this calculation

and do not “know” that the unifying group has been broken into SU(3) ⊗ SU(2) ⊗ U(1).

These equations are derived assuming that all fermion masses are small compared to μ.

Rearranging these equations somewhat, we find

sin

θ =

5α(μ)

9α

(μ)

(4)

sin

α(μ)

(μ)

6π

11 log

GUT

(5)

α(μ)

GUT

6π



F − 22



log

GUT

(6)

We obtain in (4) a prediction for sin

θ(μ) independent of M

GUT

and of the number of

families.

Note that (5) gives the bound

α(μ)

≥

6π

11 log

GUT

(7)

A lower bound on the proton lifetime (and hence on M

GUT

) translates into an upper bound

on the fine structure constant. Amusingly, the stability of the world implies the weakness

of electromagnetism.

As I noted earlier, plugging in the measured value of α

, we obtain a huge value for

GUT

. I regard this as a triumph of grand unification: M

GUT

could have come out to have

a much lower scale, leading to an immediate contradiction with the observed stability of the

proton, but it didn’t. Another way of looking at it is that if we are somehow given M

GUT

and

GUT

, grand unification fixes the couplings of all three nongravitational interactions! The

point is not that this simplest try at grand unification doesn’t quite agree with experiment:

The miracle is that it works at all.

It is beyond the scope of this book to discuss in detail the comparison of (4), (5), and

(6) with experiment. To do serious phenomenology, one has to include threshold effects

(see exercise VII.6.1), higher order corrections, and so on. To make a long story short,

after grand unified theory came out there was enormous excitement over the possibility

of proton decay. Alas, the experimental lower bound on the proton lifetime was eventually

pushed above the prediction. This certainly does not mean the demise of the notion of

grand unification. Indeed, as I mentioned earlier, the perfect fit is enough to convince

most particle theorists of the essential correctness of the idea. Over the years people have

proposed adding various hypothetical particles to the theory to promote proton longevity.

416 | VII. Grand Unification

The idea is that these particles would affect the renormalization group flow and hence

GUT

. The proton lifetime is actually not the most critical issue. With more accurate

measurements of α

and of θ , it was found that the three couplings do not quite meet at

a point. Indeed, for believers in low energy supersymmetry, part of their faith is founded

on the fact that with supersymmetric particles included, the three coupling constants do

meet.

But skeptics of course can point to the extra freedom to maneuver.

Branching ratios

You may have realized that (1), (2), and (3) are not specific for SU(5): they hold as long

as SU(3) ⊗ SU(2) ⊗ U(1) is unified into some simple group (simple so that there is only

one gauge coupling g).

Let us now focus on SU(5). Recall that we decompose the SU(5) index μ, which can

take on five values, into two types. In other words, the index μ is labeled by {α, i}, where α

takes on three values and i takes on two values. The gauge bosons in SU(5) correspond to

the 24 independent components of the traceless hermitean field A

(μ, ν = 1,2,...,5)

transforming as the adjoint representation. Focusing on the group theory of SU(5),we

will suppress Lorentz indices, spinor indices, etc. Clearly, the eight gauge bosons in SU(3)

transform an index of type α into an index of type α, while the three gauge bosons in SU(2)

transform an index of type i into an index of type i. Then there is the U(1) gauge boson

that couples to the hypercharge

Y . (Of course, you know what I mean by my somewhat

loose language: The SU(3) gauge bosons transform fields carrying a color index into a

field carrying a color index.)

The fun comes with the gauge bosons A

and A

, which transform the index α into

the index i and vice versa. Since α takes on three values, and i takes on two values, there

are 6 + 6 = 12 such gauge bosons, thus accounting for all the gauge bosons in SU(5).In

other words, 24 → (8, 1) + (1, 3) +(1, 1) + (3, 2) + (3

∗

,2). We will now see explicitly that

the exchange of these bosons between quarks and leptons leads to proton decay.

We merely have to write down the terms in the Lagrangian involving the coupling of

the bosons A

and A

to fermions and draw the appropriate Feynman diagrams. I will

go through part of the group theoretic analysis, leaving you to work out the rest. Simply

by contracting indices we see that the boson A

acting on ψ

takes it to ψ

and acting on

νρ

takes it to ψ

μρ

. Let us look at what A

does, using your result from exercise VII.5.1.

It takes

= e

−

→ ψ

d (8)

αβ

=¯u → ψ

5β

= u (9)

and

α4

= d → ψ

= e

(10)

See, e.g., F. Wilczek, in: V. Fitch et al., eds., Critical Problems in Physics, p. 297.

VII.6. Protons Are Not Forever | 417

u u

Figure VII.6.2

Thus, the exchange of A

generates the process (figure VII.6.2) u + d →¯u + e

, leading to

proton decay p(uud) → π

(u ¯u) + e

. Observe that while the decay p → π

+ e

violates

both baryon number B and lepton number L, it conserves the combination B −L.

In exercise VII.6.2 you will work out the branching ratios for various decay modes. Too

bad experimentalists have not yet measured them.

Fermion masses

We might hope that with grand unification we would gain new understanding of quark

and lepton masses. Unfortunately, the situation on fermion masses in SU(5) is muddled,

and to this day nobody understands the origin of quark and lepton masses.

Introducing a Higgs field ϕ

transforming as the 5 (as indicated by the notation) we can

write the coupling

Cψ

μν

(11)

and

μν

Cψ

λρ

μνλρσ

(12)

(with ϕ

the conjugate 5

∗

), reflecting the group theoretic fact (see appendix C) that 5

∗

⊗10

contains the 5 and 10 ⊗ 10 contains the 5

∗

Since 5 → (3, 1, −

) ⊕ (1, 2,

) we see that this Higgs field is just the natural extension

of the SU(2) ⊗ U(1) Higgs doublet (1, 2,

). Not wanting to break electromagnetism, we

allow only the electrically neutral fourth component of ϕ to acquire a vacuum expectation

value. Setting ϕ

=v, we obtain (up to uninteresting overall constants)

Cψ

α4

+ ψ

Cψ

⇒ m

= m

(13)

and

αβ

Cψ

γ 5

αβγ

⇒ m

= 0 (14)

418 | VII. Grand Unification

The larger symmetry yields a mass relation m

= m

at the unification scale; we again

have to apply the renormalization group flow. It is worth noting that the mass relation

= m

comes about because as far as the fermions are concerned, SU(5) has been only

broken down to SU(4) by ϕ. The trouble is that we obtain more or less the same relation

for each of the three families, since most of the running occurs between the unification

scale M

GUT

and the top quark mass so that threshold effects give only a small correction.

Putting in numbers one gets something like

∼

∼ 3 (15)

Let us use this to predict the down sector quark masses in terms of the lepton masses.

The formula m

∼ 3m

works rather well and provides indirect evidence that there can

only be three families since the renormalization group flow depends on F . The formula

∼ 3m

is more or less in the ballpark, depending on what “experimental” value one

takes for m

. The formula for m

, on the other hand, is downright embarrassing. People

mumble something about the first family being so light and hence other effects, such as

one-loop corrections might be important. At the cost of making the theory uglier, people

also concoct various schemes by introducing more Higgs fields, such as the 45, to give

mass to fermions.

Note that in one respect SU(5) is not as “economical” as SU(2) ⊗ U(1), in which the

same Higgs field that gives mass to the gauge bosons also gives mass to the fermions.

The universe is not empty, but almost

I mention in passing another triumph of grand unification: its ability to explain the origin

of matter in our universe. It has long behooved physicists to understand two fundamental

facts about the universe: (1) the universe is not empty, and (2) the universe is almost empty.

To physicists, (1) means that the universe is not symmetric between matter and antimatter,

that is, the net baryon number N

is nonzero; and (2) is quantified by the strikingly small

observed value N

∼ 10

−10

of the ratio of the number of baryons to the number of

photons.

Suppose we start with a universe with equal quantities of matter and antimatter. For the

universe to evolve into the observed matter dominated universe, three conditions must be

satisfied: (1) The laws of the universe must be asymmetric between matter and antimatter.

(2) The relevant physical processes had to be out of equilibrium so that there was an arrow

of time. (3) Baryon number must be violated.

We know for a fact that conditions (1) and (2) indeed hold in the world: There is

CP violation in the weak interaction and the early universe expanded rapidly. As for

(3), grand unification naturally violates baryon number. Furthermore, while proton decay

(suppressed by a factor of 1/M

GUT

in amplitude) proceeds at an agonizingly slow rate (for

those involved in the proton decay experiment!), in the early universe, when the X and

Y bosons are produced in abundance, their fast decays could easily drive baryon number

VII.6. Protons Are Not Forever | 419

violation. The suppression factor 1/M

GUT

does not come in. I have no doubt that eventually

the number 10

−10

measuring “the amount of dirt in the universe” will be calculated in

some grand unified theory.

Hierarchy

I promised you that the Weisskopf phenomenon would come back to haunt us. That the

grand unification mass scale M

GUT

naturally comes out so large counts as a triumph,

but it also leads to a problem known as the hierarchy problem. The hierarchy refers to

the enormous ratio M

GUT

, where M

denotes the electroweak unification scale, of

order 10

Gev. I will sketch this rather murky subject. Look at the Higgs field ϕ respon-

sible for breaking electroweak theory. We don’t know its renormalized or physical mass

precisely, but we do know that it is of order M

. Imagine calculating the bare pertur-

bation series in some grand unified theory—the precise theory does not enter into the

discussion—starting with some bare mass μ

for ϕ. The Weisskopf phenomenon tells

us that quantum correction shifts μ

by a huge quadratically cutoff dependent amount

δμ

∼ f



∼ f

GUT

, where we have substituted for  the only natural mass scale

around, namely M

GUT

, and where f denotes some dimensionless coupling. To have the

physical mass squared μ

=μ

+δμ

come out to be of order M

, something like 28 or-

ders of magnitude smaller than M

GUT

, would require an extremely fine-tuned and highly

unnatural cancellation between μ

and δμ

. How this could happen “naturally” poses a

severe challenge to theoretical physicists.

Naturalness

The hierarchy problem is closely connected with the notion of naturalness dear to the the-

oretical physics community. We naturally expect that dimensionless ratios of parameters

in our theories should be of order unity, where the phrase “order unity” is interpreted lib-

erally between friends, say anywhere from 10

−2

or 10

−3

to 10

or 10

. Following ’t Hooft,

we can formulate a technical definition of naturalness: The smallness of a dimensionless

parameter η would be considered natural only if a symmetry emerges in the limit η → 0.

Thus, fermion masses could be naturally small, since, as you will recall from chapter II.1,

a chiral symmetry emerges when a fermion mass is set equal to zero. On the other hand,

no particular symmetry emerges when we set either the bare or renormalized mass of a

scalar field equal to zero. This represents the essence of the hierarchy problem.

Exercises

VII.6.1 Suppose there are F



new families of quarks and leptons with masses of order M



. Adopting the crude

approximation described in exercise VI.8.2 of ignoring these families for μ below M



and of treating M



420 | VII. Grand Unification

as negligible for μ above M



, run the renormalization group flow and discuss how various predictions,

such as proton lifetime, are changed.

VII.6.2 Work out proton decay in detail. Derive relations between the following decay rates: (p → π

(p → π

¯ν), (n →π

−

), and (n → π

¯ν).

VII.6.3 Show that SU(5) conserves the combination B −L. For a challenge, invent a grand unified theory that

violates B − L.

VII.7 SO(10) Unification

Each family into a single representation

At the end of chapter VII.5 we felt we had good reason to think that SU(5) unification is

not the end of the story. Let us ask if we might be able to fit the 5 and 10

∗

into a single

representation of a bigger group G containing SU(5).

It turns out that there is a natural embedding of SU(5) into the orthogonal SO(10)

that works,

but to explain that I have to teach you some group theory. The starting point

is perhaps somewhat surprising: We go back to chapter II.3, where we learned that the

Lorentz group SO(3, 1), or its Euclidean cousin SO(4), has spinor representations. We

will now generalize the concept of spinors to d-dimensional Euclidean space. I will work

out the details for d even and leave the odd dimensions as an exercise for you. You might

also want to review appendix B now.

Clifford algebra and spinor representations

Start with an assertion. For any integer n we claim that we can find 2n hermitean matrices

(i = 1, 2,

...

,2n) that satisfy the Clifford algebra

{γ

, γ

}=2δ

(1)

In other words, to prove our claim we have to produce 2n hermitean matrices γ

that

anticommute with each other and square to the identity matrix. We will refer to the γ

’s as

the γ matrices for SO(2n).

For n = 1, it is a breeze: γ

= τ

and γ

= τ

. There you are.

Howard Georgi told me that he actually found SO(10) before SU(5).