Zee A. Quantum Field Theory in a Nutshell
Подождите немного. Документ загружается.

This page intentionally left blank

VIII.1
Gravity as a Field Theory
and the Kaluza-Klein Picture
Including gravity
Field theory texts written a generation ago typically do not even mention gravity. The
gravitational interaction, being so much weaker than the other three interactions, was
simply not included in the education of particle physicists. The situation has changed with
a vengeance: The main drive of theoretical high energy physics today is the unification of
gravity with the other three interactions, with string theory the main candidate for a unified
theory.
From a course on general relativity you would have learned about the Einstein-Hilbert
action for gravity
S =
1
16πG
d
4
x
√
−gR ≡
d
4
x
√
−gM
2
P
R (1)
where g = det g
μν
denotes the determinant of the curved metric g
μν
of spacetime, R is
the scalar curvature, and G is Newton’s constant. Let me remind you that the Riemann
curvature tensor
R
λ
μνκ
= ∂
ν
λ
μκ
− ∂
κ
λ
μν
+
σ
μκ
λ
νσ
−
σ
μν
λ
κσ
(2)
is constructed out of the Riemann-Christoffel symbol (recall chapter I.11):
λ
μν
=
1
2
g
λρ
(∂
ν
g
ρμ
+ ∂
μ
g
ρν
− ∂
ρ
g
μν
) (3)
The Ricci tensor is defined by R
μκ
=R
ν
μνκ
and the scalar curvature by R = g
μν
R
μν
. Varying
S gives us
1
the Einstein field equation
R
μν
−
1
2
g
μν
R =−8πGT
μν
(4)
The Einstein-Hilbert action is uniquely determined if we require the action to be coor-
dinate invariant and to involve two powers of spacetime derivative. As you can see from
1
See, e.g., S. Weinberg, Gravitation and Cosmology, p. 364.

434 | VIII. Gravity and Beyond
(2) and (3) the scalar curvature R involves two powers of derivative and the dimensionless
field g
μν
and thus has mass dimension 2. Hence G
−1
must have mass dimension 2. The
second form in (1) emphasizes this point and is often preferred in modern work on grav-
ity. (The modified Planck mass M
P
≡ 1/
√
16πG differs from the usual Planck mass by a
trivial factor, much like the relation between h and .)
The theory sprang from Einstein’s profound intuition regarding the curvature of space-
time and is manifestly formulated in terms of geometric concepts. In many textbooks,
Einstein’s theory is developed, and rightly so, in purely geometric terms.
On the other hand, as I hinted back in chapter I.6, gravity can be treated on the same
footing as the other interactions. After all, the graviton may be regarded as just another
elementary particle like the photon. The action (1), however, does not look anything like
the field theories we have studied thus far. I will now show you that in fact it does have the
same kind of structure.
Gravity as a field theory
Let us write g
μν
= η
μν
+ h
μν
, where η
μν
denotes the flat Minkowski metric and h
μν
the
deviation from the flat metric. Expand the action in powers of h
μν
. In order not to drown
in a sea of Lorentz indices, let us suppress them for a first go-around. Merely from the
fact that the scalar curvature R involves two derivatives ∂ in its definition, we see that the
expansion must have the schematic form
S =
d
4
x
1
16πG
(∂h∂h + h∂h∂h + h
2
∂h∂h +
...
) (5)
after dropping total divergences. As I remarked in chapter I.11, the field h
μν
(x) describes
a graviton in flat space and is to be treated like any other field. The first term ∂h∂h, which
governs how the graviton propagates, is conceptually no different than the first term in the
action for a scalar field ∂ϕ∂ϕ or for the photon field ∂A∂A. The terms cubic and higher in
h determine the interaction of the graviton with itself.
The Einstein-Hilbert action in the weak field expansion is structurally reminiscent of the
Yang-Mills action, which may be written in schematic form as S =
d
4
x(1/g
2
)(∂A∂A +
A
2
∂A +A
4
). As I explained in chapter IV.5, we understand the self interaction of the Yang-
Mills bosons physically: The bosons themselves carry the charge to which they couple.
We can understand the self interaction of the graviton similarly: The graviton couples to
anything carrying energy and momentum, and it certainly carries energy and momentum.
In contrast, the photon does not couple to itself.
We say that Yang-Mills and Einstein theories are nonlinear, while Maxwell theory is
linear. The former are hard, the latter easy.
But while the Yang-Mills action terminates, the Einstein-Hilbert action, because of the
presence of
√
−g and of the inverse of g
μν
, is an infinite series in the graviton field h
μν
.
The other major difference is that while Yang-Mills theory is renormalizable, gravity is
notoriously nonrenormalizable, as we argued by dimensional analysis in chapter III.2. We
are now in a position to see this explicitly. Consider the self energy correction to the graviton

VIII.1. Gravity as a Field Theory | 435
(a)
(b)
Figure VIII.1.1
propagator shown in figure VIII.1.1a. We see from the second term in (5) that the three-
graviton coupling involves two powers of momentum. Thus the Feynman integral goes as
d
4
k(kkkk/k
2
k
2
), with four powers of k in the numerator from the two vertices and four
powers in the denominator from the propagators. Taking out two powers of momentum to
extract the coefficient of ∂h∂h, we see that the correction to 1/G is quadratically divergent.
Because of the explicit powers of momentum in the coupling, the divergence gets worse
and worse as we go to higher and higher order. Compare figure VIII.1.1b to 1a: We have
three more propagators, worth ∼1/k
6
, and one more loop integration
d
4
k, but two more
vertices ∼ k
4
. The degree of divergence goes up by 2. Of course we already knew all this
by dimensional analysis.
As mentioned in chapter I.11 the fundamental definition
T
μν
(x) =−
2
√
−g
δS
M
δg
μν
(x)
tells us that coupling of the graviton to matter (in the weak field limit) can be included by
adding the term
−
d
4
x
1
2
h
μν
T
μν
(6)
to the action, where T
μν
stands for the (flat spacetime) stress-energy tensor of all the matter
fields of the world, a matter field being any field that is not the graviton field. Thus, with
the inclusion of matter (5) is modified schematically
2
to
S =
d
4
x[
1
16πG
(∂h∂h + h∂h∂h + h
2
∂h∂h +
...
) + (hT +
...
)] (7)
In chapter IV.5 I noted that we can bring Yang-Mills theory into the same convention
commonly used in Maxwell theory by a trivial rescaling A → gA. Similarly, we can also
bring Einstein theory into the same convention by rescaling the graviton field h
μν
→
√
Gh
μν
so that the action becomes (to ease writing we absorb 16π into G whenever we
feel like it)
S =
d
4
x (∂h∂h +
√
Gh∂h∂h + Gh
2
∂h∂h +
...
+
√
GhT )
2
If this is to represent an expansion of S in powers of h, then strictly speaking, if we display the terms cubic
and quartic in the Einstein-Hilbert action, we should also display the contribution coming from the terms of
higher order in h contained in T
μν
(x) =−(2/
√
−g)δS
M
/δg
μν
(x).

436 | VIII. Gravity and Beyond
We see explicitly that
√
16πG =1/M
P
measures the strength of the graviton coupling to
itself and to all other fields. Once again, the enormity of M
P
(compared to the scale of the
strong interaction, say) indicates the feebleness of gravity.
Here we expanded g
μν
around a flat metric but we could just as well expand g
μν
=
¯g
μν
+ h
μν
, with ¯g
μν
a curved metric, that of a black hole (see chapter V.7) for instance.
Determining the weak field action
After this index free survey we are ready to tackle the indices. We would like to determine
the first term ∂h∂h in (7) so that we can obtain the graviton propagator. Thus, we have to
expand the action S ≡ M
2
P
d
4
x
√
−gg
μν
R
μν
up to and including order h
2
. From (2) and
(3) we see that the Ricci tensor R
μν
starts in O(h) so that it suffices to evaluate
√
−gg
μν
to
O(h). That’s easy: As we have already seen in chapter I.11, g =−[1 +η
μν
h
μν
+O(h
2
)] and
g
μν
= η
μν
− h
μν
+ O(h
2
) so that
√
−gg
μν
= η
μν
− h
μν
+
1
2
η
μν
h + O(h
2
), where we have
defined h ≡ η
μν
h
μν
. We now must calculate R
μν
to O(h
2
), a straightforward but tedious
task starting from (2) and (3).
In line with the spirit of this book, which is to avoid tedious calculation whenever
possible, I will now show you how to get around this. We invoke symmetry considerations!
Under a general coordinate transformation x
μ
→x
μ
=x
μ
−ε
μ
(x) the metric changes
to g
μν
= (∂x
μ
/∂x
σ
)(∂x
ν
/∂x
τ
)g
στ
. Plugging in g
μν
= η
μν
− h
μν
+
...
, lowering the in-
dices (with η
μν
to this order), and using (∂x
μ
/∂x
σ
) = δ
μ
σ
−∂
σ
ε
μ
, we find, treating ∂
μ
ε
ν
as
of the same order as h
μν
:
h
μν
= h
μν
+ ∂
μ
ε
ν
+ ∂
ν
ε
μ
(8)
Note the structural similarity to the electromagnetic gauge transformation A
μ
= A
μ
−
∂
μ
. Very nice! We will explore the sense in which gravity can be regarded as a gauge
theory in more detail later.
We are looking for the terms in the action quadratic in h and quadratic in ∂. Lorentz
invariance tells us that there are four possible terms (To see this, first write down terms
with the indices on the two ∂ matching, then the terms with the index on a ∂ matching an
index on an h, and so on):
S =
d
4
x(a∂
λ
h
μν
∂
λ
h
μν
+ b∂
λ
h
μ
μ
∂
λ
h
ν
ν
+ c∂
λ
h
λν
∂
μ
h
μν
+ dh
λ
λ
∂
μ
∂
ν
h
μν
)
with four unknown constants a, b, c, and d . Now vary S with δh
μν
= ∂
μ
ε
ν
+ ∂
ν
ε
μ
, inte-
grating by parts freely. For example,
δ(∂
λ
h
μν
∂
λ
h
μν
) = 2[∂
λ
(2∂
μ
ε
ν
)](∂
λ
h
μν
)“ = ”4ε
ν
∂
2
∂
μ
h
μν
Since there are three objects linear in h, linear in ε, and cubic in ∂ (namely ε
ν
∂
2
∂
ν
h and
ε
ν
∂
ν
∂
λ
∂
μ
h
λμ
in addition to the one already shown) the condition δS = 0 gives three equa-
tions, just enough to fix the action up to an overall constant, corresponding to Newton’s
constant. The invariant combination turns out to be
I ≡
1
2
∂
λ
h
μν
∂
λ
h
μν
−
1
2
∂
λ
h
μ
μ
∂
λ
h
ν
ν
− ∂
λ
h
λν
∂
μ
h
μν
+ ∂
ν
h
λ
λ
∂
μ
h
μν
(9)

VIII.1. Gravity as a Field Theory | 437
Thus, even if we had never heard of the Einstein-Hilbert action we could still determine
the action for gravity in the weak field limit by requiring that the action be invariant under
the transformation (8). This is hardly surprising since coordinate invariance determines
the Einstein-Hilbert action. Still, it is nice to construct gravity “from scratch.”
Referring to (6), we can now write the weak field expansion of S as
S
wfg
=
d
4
x
1
32πG
I −
1
2
h
μν
T
μν
without having to expand R to O(h
2
). The coefficient of I is fixed by the requirement that
we reproduce the usual Newtonian gravity (see later).
The graviton propagator
As we anticipated in (5) the action S
wfg
indeed has the same quadratic structure of all
the field theories we have studied, and so as usual the graviton propagator is just the
inverse of a differential operator. But just as in Maxwell and Yang-Mills theories the relevant
differential operator in Einstein-Hilbert theory does not have an inverse because of the
“gauge invariance” in (8).
No problem. We have already developed the Faddeev-Popov method to deal with this
difficulty. In fact, for my limited purposes here, to derive the graviton propagator in flat
spacetime, I don’t even need the full-blown Faddeev-Popov formalism with ghosts and all.
3
Indeed, recall from chapter III.4 that for the Feynman gauge (ξ = 1) we simply add (∂A)
2
to the invariant
1
2
F
μν
F
μν
= ∂
μ
A
ν
(∂
μ
A
ν
− ∂
ν
A
μ
)“ = ” − A
μ
η
μν
∂
2
A
ν
− (∂A)
2
thus canceling the last term. Inverting the differential operator −η
μν
∂
2
we obtain the
photon propagator in the Feynman gauge −iη
μν
/k
2
. We play the same “trick” for gravity.
After staring at
I =
1
2
∂
λ
h
μν
∂
λ
h
μν
−
1
2
∂
λ
h
μ
μ
∂
λ
h
ν
ν
− ∂
λ
h
λν
∂
μ
h
μν
+ ∂
ν
h
λ
λ
∂
μ
h
μν
for a while, we see that by adding (∂
μ
h
μν
−
1
2
∂
ν
h
λ
λ
)
2
we can knock off the last two terms in
I so that S
wfg
effectively becomes
S
wfg
=
d
4
x
1
2
1
32πG
∂
λ
h
μν
∂
λ
h
μν
−
1
2
∂
λ
h∂
λ
h
− h
μν
T
μν
(10)
In other words, the freedom in choosing h
μν
in (8) allows us to impose the so-called
harmonic gauge condition
∂
μ
h
μ
ν
=
1
2
∂
ν
h
λ
λ
(11)
(the linearized version of ∂
μ
(
√
−gg
μν
) = 0.)
3
This is because (8) does not involve the field h
μν
, just as in the Maxwell case but unlike the Yang-Mills
case. Since we do not intend to calculate loop diagrams in quantum gravity, we do not need the full power of the
Faddeev-Popov method.

438 | VIII. Gravity and Beyond
Writing (10) in the form
S =
1
32πG
d
4
x
h
μν
K
μν;λσ
(−∂
2
)h
λσ
+ O(h
3
)
we see that we have to invert the matrix
K
μν;λσ
≡
1
2
(η
μλ
η
νσ
+ η
μσ
η
νλ
− η
μν
η
λσ
)
regarding μν and λσ as the two indices. Note that we have to maintain the symmetry of
h
μν
. In other words, we are dealing with matrices acting in a linear space spanned by
symmetric two-index tensors. Thus, the identity matrix is actually
I
μν;λσ
≡
1
2
(η
μλ
η
νσ
+ η
μσ
η
νλ
)
You can check that K
μν;λσ
K
λσ
;ρω
= I
μν;ρω
so that K
−1
= K. Thus, in the harmonic gauge
the graviton propagator in flat spacetime is given by (scaling out Newton’s constant)
D
μν , λσ
(k) =
1
2
η
μλ
η
νσ
+ η
μσ
η
νλ
− η
μν
η
λσ
k
2
+ iε
(12)
Newton from Einstein
Varying (10) with respect to h
μν
we obtain the Euler-Lagrange equation of motion
4
1
32πG
(−2∂
2
h
μν
+ η
μν
∂
2
h) − T
μν
= 0. Taking the trace, we find ∂
2
h = 16πGT (with T ≡
η
μν
T
μν
) and so we obtain
5
∂
2
h
μν
=−16πG(T
μν
−
1
2
η
μν
T) (13)
In the static limit, T
00
is the dominant component
6
of the stress-energy tensor and (13)
reduces to
∇
2
φ =4πGT
00
upon recalling from chapter I.5 that the Newtonian gravitational
potential φ ≡
1
2
h
00
. We have just derived Poisson’s equation for φ.
Incidentally, this suggests another way of avoiding the tedious task of expanding the
Einstein-Hilbert action (and hence R) to O(h
2
) if you are willing to accept the Einstein
field equation (4) as given. You need expand R
μν
only to O(h) to obtain (13) from (4), and
from (13) you can reconstruct the action to O(h
2
). Indeed, from (2) and (3) you easily get
R
μν
=
1
2
(−∂
2
h
μν
+ ∂
μ
∂
λ
h
λ
ν
+ ∂
ν
∂
λ
h
λ
μ
− ∂
μ
∂
ν
h
λ
λ
) + O(h
2
) →−
1
2
∂
2
h
μν
+ O(h
2
)
with the further simplification in harmonic gauge. But this is not quite fair since con-
siderable technology
7
(Palatini identity and all the rest) is needed to derive (4) from (1).
4
Note that the flat spacetime energy momentum conservation ∂
μ
T
μν
=0 together with the equation of motion
implies ∂
2
(∂
μ
h
μν
−
1
2
∂
ν
h) = 0.
5
Thus, the Einstein equation in vacuum R
μν
= 0 reduces to ∂
2
h
μν
= 0; hence the name “harmonic.”
6
Note that, in contrast to T
00
, h
00
does not dominate the other components of h
μν
.
7
See S. Weinberg, Gravitation and Cosmology, pp. 290 and 364.
VIII.1. Gravity as a Field Theory | 439
Einstein’s theory and the deflection of light
Consider two particles with stress-energy tensors T
μν
(1)
and T
μν
(2)
respectively interacting via
the exchange of a graviton. The scattering amplitude is then (up to some overall constant
not essential for our purposes here) given by
GT
μν
(1)
D
μν , λσ
(k)T
λσ
(2)
=
G
2k
2
(2T
μν
(1)
T
(2)μν
− T
(1)
T
(2)
)
For nonrelativistic matter T
00
is much larger than the other components T
0j
and T
ij
(as
I have just remarked), so the scattering amplitude between two lumps of nonrelativistic
matter (say, the earth and you) is proportional to
G
2k
2
(2T
00
(1)
T
00
(2)
− T
00
(1)
T
00
(2)
) =
G
2k
2
T
00
(1)
T
00
(2)
As explained way back in chapters I.4 and I.5, the interaction potential is given by the
Fourier transform of the scattering amplitude, namely
G
d
3
xd
3
x
T
(1)00
(x)T
(2)00
(x
)
d
3
ke
i
k
.
(x−x
)
1
k
2
and thus for two well-separated objects we recover the Newtonian potential GM
(1)
M
(2)
/r.
We are now able to address the issue raised at the end of chapter I.5. Suppose a particle
theorist, Dr. Gravity, wants to propose a theory of gravity to rival Einstein’s theory. Dr. G
claims that gravity is due to the exchange of a spin 2 particle with a teeny mass m
G
coupled
to the stress-energy tensor T
μν
. In chapter I.5 we worked out the propagator of a massive
spin 2 particle, namely
D
spin 2
μν , λσ
(k) =
1
2
(G
μλ
G
νσ
+ G
μσ
G
νλ
−
2
3
G
μν
G
λσ
)/(k
2
− m
2
G
+ iε)
with G
μν
= η
μν
− k
μ
k
ν
/m
2
G
(after a trivial notational adjustment). Since the particle is
coupled to a conserved source k
μ
T
μν
= 0 we can replace G
μν
by η
μν
. Thus, in the limit
m
G
→ 0 we have the propagator
D
spin 2
μν , λσ
(k) =
1
2
η
μλ
η
νσ
+ η
μσ
η
νλ
−
2
3
η
μν
η
λσ
k
2
+ iε
(14)
Compare this with (12). Dr. G’s propagator differs from Einstein’s:
2
3
versus 1. Remarkably,
gravity is not generated by an almost massless spin 2 particle. The “
2
3
discontinuity”
between (12) and (14) was discovered in 1970 independently by Iwasaki, by van Dam and
Veltman, and by Zakharov.
In Dr. G’s theory (with his own gravitational coupling G
G
), the interaction between two
particles is given by
G
G
T
μν
(1)
D
μν , λσ
(k)T
λσ
(2)
=
G
G
2k
2
(2T
μν
(1)
T
(2)μν
−
2
3
T
(1)
T
(2)
)
For two lumps of nonrelativistic matter this becomes
G
G
2k
2
(2T
00
(1)
T
00
(2)
−
2
3
T
00
(1)
T
00
(2)
) =
4
3
G
G
2k
2
T
00
(1)
T
00
(2)
Dr. G simply takes his G
G
=
3
4
G and his theory passes all experimental tests.

440 | VIII. Gravity and Beyond
But wait! There is also the famous 1919 observation of the deflection of starlight by
the sun, and the photon is definitely not a lump of nonrelativistic matter. Indeed, recall
from chapter I.11 (or from your course on electromagnetism) that T ≡ T
μ
μ
vanishes for
the photon. Thus, taking T
μν
(1)
and T
μν
(2)
to be the stress-energy tensor of the sun and of the
photon respectively, Einstein would have for the scattering amplitude (G/2k
2
)2T
μν
(1)
T
(2)μν
while Dr. G would have (G
G
/2k
2
)2T
μν
(1)
T
(2)μν
=
3
4
(G/2k
2
)2T
μν
(1)
T
(2)μν
. Dr. G would have
predicted a deflection angle of 3GM/R instead of 4GM/R (with M and R the mass
and radius of the sun). On the Brazilian island of Sobral in 1919 Einstein triumphed
over Dr. G.
As explained in chapter I.5, while a massive spin 2 particle has 5 degrees of freedom the
massless graviton has only 2. (I give an analysis of the helicity ±2 structure of one graviton
exchange in appendix 2.) The 5 degrees of freedom may be thought of as consisting of the
helicity ±2 degrees of freedom we want plus 2 helicity ±1 and a helicity 0 degrees of
freedom. The coupling of the helicity ±1 degrees of freedom vanishes because k
μ
T
μν
=0.
Thus, effectively, we are left with an extra scalar coupling to the trace T ≡ η
μν
T
μν
of the
stress-energy tensor; as we can see plainly the discrepancy indeed resides in the last term
of (12) and (14).
You should be disturbed that a measurement of the deflection of starlight can show
that a physical quantity, the graviton mass m
G
, is mathematically zero rather than less
than some extremely small value. This apparent paradox was resolved by A. Vainshtein in
1972.
8
He found that Dr. G’s theory contains a distance scale
r
V
=
GM
m
4
G
1
5
in the gravitational field around a body of mass M. The helicity 0 degree of freedom
becomes effective only on the distance scales r r
V
. Inside the Vainshtein radius r
V
, the
gravitational field is the same as in Einstein’s theory and experiments cannot distinguish
between Einstein’s and Dr. G’s theories. With the current astrophysical bound m
G
(10
24
cm)
−1
and M the mass of the sun, r
V
comes out to be much larger than the size
of the solar system. In other words, the apparent paradox arose because of an interchange
of limits: We can take either the characteristic distance of the measurement r
obs
(the radius
of the sun in the deflection of starlight) or the Vainshtein radius r
V
to infinity first.
So all is well: Dr. G’s theory is consistent with current measurements provided that
he takes m
G
small enough. What he is not allowed to do is use the one graviton exchange
approximation. Instead, he should solve the massive analog of Einstein’s field equation (4)
around a massive body such as the sun, as Vainshtein did. This is equivalent to expanding
to all orders in the graviton field h and resumming: In Feynman diagram language we
8
A. I. Vainshtein, Phys. Lett. 39B:393, 1972; see also C. Deffayet, G. Dvali, G. Gabadadze, and A. I. Vainshtein,
Phys. Rev. D65:044026, 2002.
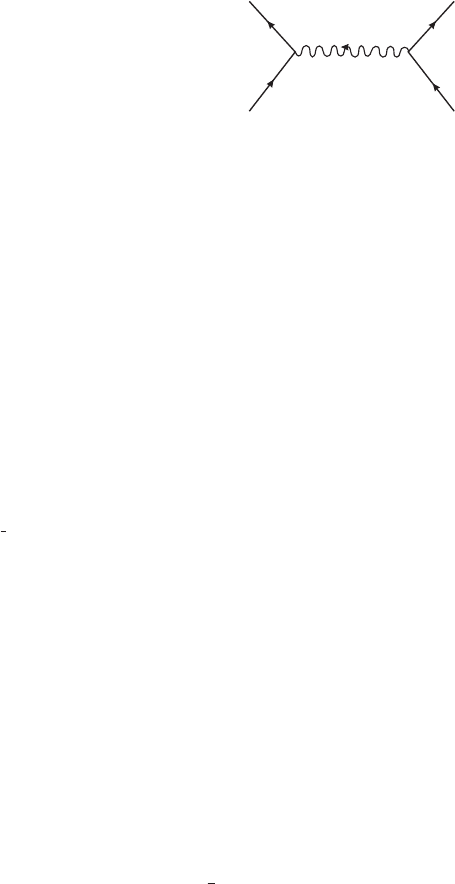
VIII.1. Gravity as a Field Theory | 441
q
k
1
k
2
p
1
p
2
Figure VIII.1.2
have an infinite number of diagrams corresponding to the sun emitting 1, 2, 3,
...
, ∞
gravitons respectively. The paradox is formally resolved by noting that the higher orders
are increasingly singular as m
G
→ 0.
The gravity of light
At this point, you are ready to do perturbative quantum gravity: You have the graviton
propagator (12), and you can read off the interaction between gravitons from the detailed
version of (7) and the interaction between the graviton and any other field from the term
−
1
2
h
μν
T
μν
. The only trouble is that you might “drown in a sea of indices” if you don’t watch
out, as I have already warned you.
I know of one calculation (in fact one of my favorites in theoretical physics) in which
we can beat the indices down easily. An interesting question: Einstein said that light
is deflected by a massive object, but is light deflected gravitationally by light? Tolman,
Ehrenfest, and Podolsky discovered that in the weak field limit two light beams moving
in the same direction do not interact gravitationally, but two light beams moving in the
opposite directions do. Surprising, eh?
The scattering of two photons k
1
+k
2
→p
1
+p
2
via the exchange of a graviton is given
by the Feynman diagram in figure VIII.1.2, with the momentum transfer q ≡p
1
−k
1
, plus
another diagram with p
1
and p
2
interchanged. The Feynman rule for coupling a graviton
to two photons can be read off from
h
μν
T
μν
=−h
μν
(F
μλ
F
ν
λ
−
1
4
η
μν
F
ρλ
F
ρλ
)
but all we need is that the interaction involve two powers of spacetime derivatives ∂ acting
on the electromagnetic potential A
μ
so that the graviton-photon-photon vertex involves
2 powers of momenta, one from each photon. Hence the scattering amplitude (with all
Lorentz indices suppressed) has the schematic form ∼ (k
1
p
1
)D(k
2
p
2
). The η’s in the
graviton propagator D tie the indices on (k
1
p
1
) and (k
2
p
2
) together. (We have suppressed
the polarization vectors of the photons, imagining that they are to be averaged over in
the amplitude squared.) Referring to (12), we see that the amplitude is the sum of three
terms such as ∼ (k
1
.
p
1
)(k
2
.
p
2
)/q
2
, ∼ (k
1
.
k
2
)(p
1
.
p
2
)/q
2
, and ∼ (k
1
.
p
2
)(k
2
.
p
1
)/q
2
.
Since according to Fourier the long distance part of the interaction potential is given by
