Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

242 | IV. Symmetry and Symmetry Breaking

condition on d

eff

/dϕ

not at ϕ = 0 but at ϕ equal to some arbitrarily chosen mass M.

(Recall that ϕ has the dimension of mass.) Thus, the second condition reads

eff

dϕ



ϕ=M

= λ(M) (18)

where λ(M) is a coupling manifestly dependent on M .

Plugging

eff

(ϕ) = (

λ +

(16π)

log



+ C)ϕ

+ O(λ

)

into (18) we see that λ(M) is equal to λ plus O(λ

) corrections, among which is a term like

log M. We can get a clean relation by differentiating λ(M) :

dλ(M)

16π

+ O(λ

)

16π

λ(M)

+ O[λ(M)

] (19)

where the second equality is correct to the order indicated. This interesting relation tells us

how the coupling λ(M) depends on the mass scale M at which it is defined. Recall exercise

III.1.3. We will come back to this relation in chapter VI.7 on the renormalization group.

Meanwhile, let us press on. Using (18) to determine C and plugging it into V

eff

obtain

eff

(ϕ) =

λ(M)ϕ

λ(M)

(16π)



log

−



+ O[λ(M)

] (20)

You are no longer surprised, I suppose, that C and the cutoff  have both disappeared.

That’s a renormalizable theory for you!

The fact that V

eff

does not depend on the arbitrarily chosen M , namely, M(dV

eff

/dM) =

0, reproduces (19) to the order indicated.

Breaking by quantum fluctuations

Now we can answer the motivating question: To break or not to break?

Quantum fluctuations generate a correction to the potential of the form +ϕ

log ϕ

but log ϕ

is whopping big and negative for small ϕ! The O() correction overwhelms

the classical O(

) potential +ϕ

near ϕ = 0. Quantum fluctuations break the discrete

symmetry ϕ →−ϕ.

It is easy enough to determine the minima ±ϕ

min

of V

eff

(ϕ) (which you should plot as

a function of ϕ to get a feeling for). But closer inspection shows us that we cannot take the

precise value of ϕ

min

seriously; V

eff

has the form λϕ

(1 + λ log ϕ +

...

) suggesting that

the expansion parameter is actually λ log ϕ rather than λ. [Try to convince yourself that

(

...

) starts with (λ log ϕ)

.] The minima ϕ

min

of V

eff

clearly occurs when the expansion

parameter is of order unity. In an exercise in chapter IV.7 you will see a clever way of getting

around this problem.

IV.3. Effective Potential | 243

Fermions

In (11) ϕ

plays the role of an external field while ϕ corresponds to a quantum field we

integrate over. The role of ϕ can also be played by a fermion field ψ. Consider adding

ψ(i∂ −m − fϕ)ψ to the Lagrangian. In the path integral

Z =



DϕD

ψDψe



(∂ϕ)

−V(ϕ)+

ψ(i∂−m−fϕ)ψ]

(21)

we can always choose to integrate over ψ first, obtaining

Z =



Dϕe



(∂ϕ)

−V(ϕ)]+tr log(i∂−m−fϕ)

(22)

Repeating the steps in (13) we find that the fermion field contributes

(ϕ) =+i



(2π)

tr log

p − m − fϕ

p

(23)

to V

eff

(ϕ). (The trace in (23) is taken over the gamma matrices.) Again from chapter II.5,

we see that physically V

(ϕ) represents the vacuum energy of a fermion with the effective

mass m(ϕ) ≡ m + fϕ.

We can massage the trace of the logarithm using tr log M = log det M (II.5.12) and

cyclically permuting factors in a determinant):

tr log(p − a) = tr log γ

(p − a)γ

= tr log(−p − a)

tr(log(p − a) + log(p + a)) +

tr log(−1)

tr log(−1)(p

− a

). (24)

Hence,

tr log

(p − a)

p

tr log

− a

= 2 log

− a

(25)

and so

(ϕ) = 2i



(2π)

log

− m(ϕ)

(26)

Contrast the overall sign with the sign in (14): the difference in sign between fermionic

and bosonic loops was explained in chapter II.5.

Thus, in the end the effective potential generated by the quantum fluctuations has a

pleasing interpretation: It is just the energy density due to the fluctuating energy, entirely

analogous to the zero point energy of the harmonic oscillator, of quantum fields living in

the background ϕ (see exercise IV.3.5).

Exercises

IV.3.1 Consider the effective potential in (0 + 1)-dimensional spacetime:

eff

(ϕ) = V(ϕ)+



(2π)

log

+ V



(ϕ)

+ O(

)

244 | IV. Symmetry and Symmetry Breaking

No counterterm is needed since the integral is perfectly convergent. But (0 + 1)-dimensional field theory

is just quantum mechanics. Evaluate the integral and show that V

eff

is in complete accord with your

knowledge of quantum mechanics.

IV.3.2 Study V

eff

in (1 + 1)−dimensional spacetime.

IV.3.3 Consider a massless fermion field ψ coupled to a scalar field ϕ by fϕ

ψψ in (1 + 1)-dimensional

spacetime. Show that

2π

(f ϕ)

log

(27)

after a suitable counterterm has been added. This result is important in condensed matter physics, as

we will see in chapter V.5 on the Peierls instability.

IV.3.4 Understand (14) using Feynman diagrams. Show that V

eff

is generated by an infinite number of di-

agrams. [Hint: Expand the logarithm in (14) as a series in V



(ϕ)/k

and try to associate a Feynman

diagram with each term in the series.]

IV.3.5 Consider the electrodynamics of a complex scalar field

L =−

μν



(∂

+ ieA

)ϕ

†



(∂

− ieA

)ϕ

+ μ

†

ϕ − λ(ϕ

†

ϕ)

(28)

In a universe suffused with the scalar field ϕ(x) taking on the value ϕ independent of x as in the text,

the Lagrangian will contain a term (e

†

ϕ)A

so that the effective mass squared of the photon field

becomes M(ϕ)

≡ e

†

ϕ. Show that its contribution to V

eff

(ϕ) has the form



(2π)

log

− M(ϕ)

(29)

Compare with (14) and (26). [Hint: Use the Landau gauge to simplify the calculation.] If you need help,

I strongly urge you to read S. Coleman and E. Weinberg, Phys. Rev. D7: 1883, 1973, a paragon of clarity

in exposition.

IV.4 Magnetic Monopole

Quantum mechanics and magnetic monopoles

Curiously enough, while electric charges are commonplace nobody has ever seen a mag-

netic charge or monopole. Within classical physics we can perfectly well modify one of

Maxwell’s equations to



∇



B =ρ

, with ρ

denoting the density of magnetic monopoles.

The only price we have to pay is that the magnetic field



B can no longer be represented



B =



∇×



A since otherwise



∇



B =



∇



∇×



A = ε

ij k

∂

=0 identically. Newton and

Leibniz told us that derivatives commute with each other.

So what, you say. Indeed, who cares that



B cannot be written as



∇×



A? The vector po-

tential



A was introduced into physics only as a mathematical crutch, and indeed that is

still how students are often taught in a course on classical electromagnetism. As the dis-

tinguished nineteenth-century physicist Heaviside thundered, “Physics should be purged

of such rubbish as the scalar and vector potentials; only the fields



E and



B are physical.”

With the advent of quantum mechanics, however, Heaviside was proved to be quite

wrong. Recall, for example, the nonrelativistic Schr

odinger equation for a charged particle

in an electromagnetic field:



−

(



∇−ie



+ eφ



ψ =Eψ (1)

Charged particles couple directly to the vector and scalar potentials



A and φ, which are

thus seen as being more fundamental, in some sense, than the electromagnetic fields



and



B , as I alluded to in chapter III.4. Quantum physics demands the vector potential.

Dirac noted brilliantly that these remarks imply an intrinsic conflict between quantum

mechanics and the concept of magnetic monopoles. Upon closer analysis, he found that

quantum mechanics does not actually forbid the existence of magnetic monopoles. It

allows magnetic monopoles, but only those carrying a specific amount of magnetic charge.

246 | IV. Symmetry and Symmetry Breaking

Differential forms

For the following discussion and for the next chapter on Yang-Mills theory, it is highly

convenient to use the language of differential forms. Fear not, we will need only a few

elementary concepts. Let x

be D real variables (thus, the index μ takes on D values)

and A

(not necessarily the electromagnetic gauge potential in this purely mathematical

section) be D functions of the x’s. In our applications, x

represent coordinates and, as

we will see, differential forms have natural geometric interpretations.

We call the object A ≡ A

a 1-form. The differentials dx

are treated following New-

ton and Leibniz. If we change coordinates x → x



, then as usual dx

=(∂x

/∂x

ν

)dx

ν

that A ≡A

(∂x

/∂x

ν

)dx

ν

≡ A



ν

. This reproduces the standard transforma-

tion law of vectors under coordinate transformation A



= A

(∂x

/∂x

ν

). As an example,

consider A = cos θdϕ. Regarding θ and ϕ as angular coordinates on a 2-sphere (namely

the surface of a 3-ball), we have A

= 0 and A

= cos θ . Similarly, we define a p-form as

H = (1/p!)H

...

. (Repeated indices are summed, as always.) The

“degenerate” example is that of a 0-form, call it , which is just a scalar function of the

coordinates x

. An example of a 2-form is F = (1/2!)F

μν

We now face the question of how to think about products of differentials. In an ele-

mentary course on calculus we learned that dx dy represents the area of an infinitesimal

rectangle with length dx and width dy. At that level, we more or less automatically regard

dy dx as the same as dx dy. The order of writing the differentials does not matter. However,

think about making a coordinate transformation so that x =x(x



, y



) and y =y(x



, y



) are

now functions of the new coordinates x



and y



. Now look at

dx dy =



∂x



∂x

∂y





∂y

∂x



∂y





(2)

Note that the coefficient of dx



is (∂x/∂x



)(∂y/∂y



) and that the coefficient of dy



is (∂x/∂y



)(∂y/∂x



). We see that it is much better if we regard the differentials dx

as anticommuting objects [what mathematicians would call Grassmann variables (recall

chapter (II.5)] so that dy



=−dx



and dx



= 0 = dy



. Then (2) simplifies

neatly to

dx dy =



∂x



∂y



−

∂x

∂y



∂y

∂x







≡ J(x, y; x



, y



)dx



(3)

We obtain the correct Jacobian J(x, y; x



, y



) for transforming the area element dx dy to

the area element dx



In many texts, dx dy is written as dx^dy. We will omit the wedge—no reason to clutter

up the page.

This little exercise tells us that we should define dx

=−dx

and regard the

area element dx

as directional. The area elements dx

and dx

have the same

magnitude but point in opposite directions.

IV.4. Magnetic Monopole | 247

We now define a differential operation d to act on any form. Acting on a p-form H ,it

gives by definition

dH =

∂

...

Thus, d = ∂

dx

and

dA = ∂

(∂

− ∂

)dx

In the last step, we used dx

=−dx

We see that this mathematical formalism is almost tailor made to describe electromag-

netism. If we call A ≡ A

the potential 1-form and think of A

as the electromag-

netic potential, then F = dA is in fact the field 2-form. If we write F out in terms of its

components F = (1/2!)F

μν

, then F

μν

is indeed equal to the electromagnetic field

(∂

− ∂

Note that x

is not a form, and dx

is not d acting on a form.

If you like, you can think of differential forms as “merely” an elegantly compact notation.

The point is to think of physical objects such as A and F as entities, without having to

commit to any particular coordinate system. This is particularly convenient when one has

to deal with objects more complicated than A and F , for example in string theory. By using

differential forms, we avoid drowning in a sea of indices.

An important identity is

dd = 0 (4)

which says that acting with d on any form twice gives zero. Verify this as an exercise. In

particular dF = ddA = 0. If you write this out in components you will recognize it as a

standard identity (the “Bianchi identity”) in electromagnetism.

Closed is not necessarily globally exact

It is convenient here to introduce some jargon. A p-form α is said to be closed if dα = 0.

It is said to be exact if there exists a (p − 1)-form β such that α = dβ .

Talking the talk, we say that (4) tells us that exact forms are closed.

Is the converse of (4) true? Kind of. The Poincar

e lemma states that a closed form is

locally exact. In other words, if dH = 0 with H some p-form, then locally

H = dK (5)

for some (p − 1)-form K . However, it may or may not be the case that H = dK globally,

that is, everywhere. Actually, whether you know it or not, you are already familiar with the

Poincar

e lemma. For example, surely you learned somewhere that if the curl of a vector

field vanishes, the vector field is locally the gradient of some scalar field.

Forms are ready made to be integrated over. For example, given the 2-form F =

(1/2!)F

μν

, we can write



F for any 2-manifold M . Note that the measure is

248 | IV. Symmetry and Symmetry Breaking

already included and there is no need to specify a coordinate choice. Again, whether you

know it or not, you are already familiar with the important theorem



dH =



∂M

H (6)

with H a p-form and ∂M the boundary of a (p + 1)-dimensional manifold M .

Dirac quantization of magnetic charge

After this dose of mathematics, we are ready to do some physics. Consider a sphere

surrounding a magnetic monopole with magnetic charge g. Then the electromagnetic

field 2-form is given by F = (g/4π)dcos θdϕ. This is almost a definition of what we mean

by a magnetic monopole (see exercise IV.4.3.) In particular, calculate the magnetic flux by

integrating F over the sphere S



F = g (7)

As I have already noted, the area element is automatically included. Indeed, you might

have recognized dcos θdϕ=−sin θdθdϕas precisely the area element on a unit sphere.

Note that in “ordinary notation” (7) implies the magnetic field



B = (g/4πr

)ˆr, with ˆr the

unit vector in the radial direction.

I will now give a rather mathematical, but rigorous, derivation, originally developed by

Wu and Yang, of Dirac’s quantization of the magnetic charge g.

First, let us recall how gauge invariance works, from, for example, (II.7.3). Under a

transformation of the electron field ψ(x)→ e

i(x)

ψ(x), the electromagnetic gauge poten-

tial changes by

(x) → A

(x) +

−i(x)

∂

i(x)

or in the language of forms,

A → A +

−i

i

(8)

Differentiating, we can of course write

(x) → A

(x) +

∂

(x)

as is commonly done. The form given in (8) reminds us that gauge transformation is

defined as multiplication by a phase factor e

i(x)

, so that (x) and (x) + 2π describe

exactly the same transformation.

In quantum mechanics A is physical, pace Heaviside, and so we should ask what A

would give rise to F = (g/4π) d cos θdϕ. Easy, you say; clearly A = (g/4π) cos θdϕ. (In

checking this by calculating dA, remember that dd = 0.)

But not so fast; your mathematician friend says that dϕ is not defined at the north and

south poles. Put his objection into everyday language: If you are standing on the north pole,

what is your longitude? So strictly speaking it is forbidden to write A = (g/4π) cos θdϕ.

IV.4. Magnetic Monopole | 249

But, you are smart enough to counter, then what about A

=(g/4π)(cos θ −1)dϕ, eh?

When you act with d on A

you obtain the desired F ; the added piece (g/4π)(−1)dϕgets

annihilated by d thanks once again to the identity (4). At the north pole, cos θ = 1, A

vanishes, and is thus perfectly well defined.

OK, but your mathematician friend points out that your A

is not defined at the south

pole, where it is equal to (g/4π)(−2)dϕ.

Right, you respond, I anticipated that by adding the subscript N . I am now also forced

to define A

= (g/4π)(cos θ +1)dϕ. Note that d acting on A

again gives the desired F .

But now A

is defined everywhere except at the north pole.

In mathematical jargon, we say that the gauge potential A is defined locally, but not

globally. The gauge potential A

is defined on a “coordinate patch” covering the northern

hemisphere and extending past the equator as far south as we want as long as we do

not include the south pole. Similarly, A

is defined on a “coordinate patch” covering the

southern hemisphere and extending past the equator as far north as we want as long as

we do not include the north pole.

But what happens where the two coordinate patches overlap, for example, along the

equator. The gauge potentials A

and A

are not the same:

− A

= 2

4π

dϕ (9)

Now what? Aha, but this is a gauge theory: If A

and A

are related by a gauge transforma-

tion, then all is well. Thus, referring to (8) we require that 2(g/4π) dϕ = (1/ie)e

−i

i

for some phase function e

i

. By inspection we have e

i

= e

i2(eg/4π)ϕ

But ϕ = 0 and ϕ = 2π describe exactly the same point. In order for e

i

to make sense,

we must have e

i2(eg/4π)(2π)

= e

i2(eg/4π)(0)

= 1; in other words, e

ieg

= 1, or

g =

2π

n (10)

where n denotes an integer. This is Dirac’s famous discovery that the magnetic charge on

a magnetic monopole is quantized in units of 2π/e. A “dual” way of putting this is that if

the monopole exists then electric charge is quantized in units of 2π/g.

Note that the whole point is that F is locally but not globally exact; otherwise by (6) the

magnetic charge g =



F would be zero.

I show you this rigorous mathematical derivation partly to cut through a lot of the

confusion typical of the derivations in elementary texts and partly because this type of

argument is used repeatedly in more advanced areas of physics, such as string theory.

Electromagnetic duality

That a duality may exist between electric and magnetic fields has tantalized theoretical

physicists for a century and a half. By the way, if you read Maxwell, you will discover that he

often talked about magnetic charges. You can check that Maxwell’s equations are invariant

under the elegant transformation (



E + i



B) → e

iθ

(



E + i



B) if magnetic charges exist.

250 | IV. Symmetry and Symmetry Breaking

(a) (b)

(σ,τ)x

(τ)

Figure IV.4.1

One intriguing feature of (10) is that if e is small, then g is large, and vice versa. What

would magnetic charges look like if they exist? They wouldn’t look any different from

electric charges: They too interact with a 1/r potential, with likes repelling and opposites

attracting. In principle, we could have perfectly formulated electromagnetism in terms of

magnetic charges, with magnetic and electric fields exchanging their roles, but the theory

would be strongly coupled, with the coupling g rather than e.

Theoretical physicists are interested in duality because it allows them a glimpse into

field theories in the strongly coupled regime. Under duality, a weakly coupled field theory

is mapped into a strongly coupled field theory. This is exactly the reason why the discovery

some years ago that certain string theories are dual to others caused such enormous

excitement in the string theory community: We get to know how string theories behave in

the strongly coupled regime. More on duality in chapter VI.3.

Forms and geometry

The geometric character of differential forms is further clarified by thinking about the

electromagnetic current of a charged particle tracing out the world line X

(τ ) in D-

dimensional spacetime (see figure IV.4.1a):

(x) =



dτ

(D)

[x − X(τ)] (11)

The interpretation of this elementary formula from electromagnetism is clear: dX

/dτ is

the 4-velocity at a given value of the parameter τ (“proper time”) and the delta function

ensures that the current at x vanishes unless the particle passes through x. Note that J

(x)

is invariant under the reparametrization τ → τ



(τ ).

The generalization to an extended object is more or less obvious. Consider a string. It

traces out a world sheet X

(τ , σ) in spacetime (see figure 1b), where σ is a parameter

IV.4. Magnetic Monopole | 251

telling us where we are along the length of the string. [For example, for a closed string,

σ is conventionally taken to range between 0 and 2π with X

(τ ,0) = X

(τ ,2π).] The

current associated with the string is evidently given by

μν

(x) =



dτdσ det



∂



(D)

[x − X(τ, σ)] (12)

where ∂

≡ ∂/∂τ and so forth. The determinant is forced on us by the requirement of

invariance under reparametrization τ → τ



(τ , σ), σ → σ



(τ , σ). It follows that J

μν

is an

antisymmetric tensor. Hence, the analog of the electromagnetic potential A

coupling to

the current J

is an antisymmetric tensor field B

μν

coupling to the current J

μν

. Thus,

string theory contains a 2-form potential B =

μν

and the corresponding 3-form

field H = dB. In fact, string theory typically contains numerous p-forms.

Aharonov-Bohm effect

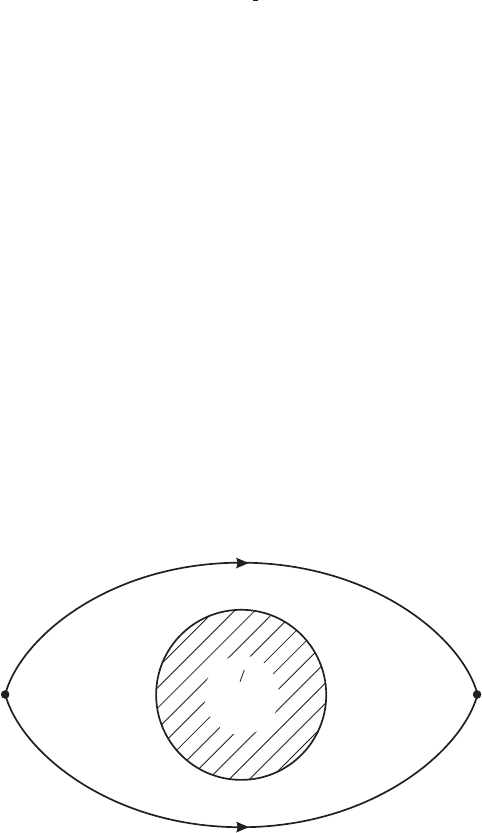
The reality of the gauge potential A was brought home forcefully in 1959 by Aharonov and

Bohm. Consider a magnetic field B confined to a region  as illustrated in figure IV.4.2.

The quantum physics of an electron is described by solving the Schr

odinger equation (1).

In Feynman’s path integral formalism the amplitude associated with a path P is modified

by a multiplicative factor e



d x

, where the line integral is evaluated along the path P .

Thus, in the path integral calculation of the probability for an electron to propagate from

a to b (fig. IV.4.2), there will be interference between the contributions from path 1 and

path 2 of the form





d x





d x



∗







d x



B = 0

Figure IV.4.2