Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

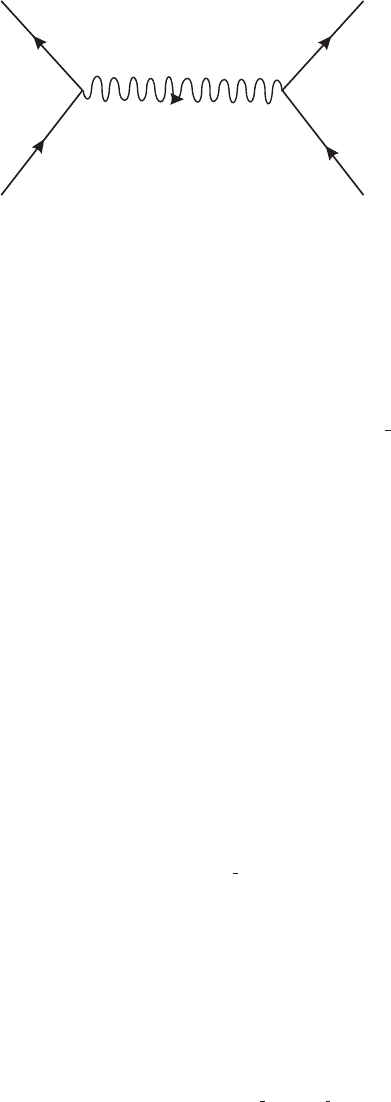
172 | III. Renormalization and Gauge Invariance

Figure III.2.2

Let’s calculate fermion-fermion scattering. The Feynman diagram in figure III.2.2 gen-

erates an amplitude (−ig)

( ¯uγ

u)[i/(k

− M

+ iε)]( ¯uγ

u), which when the momentum

transfer k is much less than M becomes i(g

)( ¯uγ

u)( ¯uγ

u). But this is just as if the

fermions are interacting via a Fermi theory of the form G(

ψγ

ψ)(

ψγ

ψ)with G =g

If we blithely calculate with the low energy effective theory G(

ψγ

ψ)(

ψγ

ψ), it cries

out that it is going to fail. Yes sir indeed, at the energy scale (1/G)

= M/g, the vector

boson is produced. New physics appears.

I find it sobering and extremely appealing that theories in physics have the ability to

announce their own eventual failure and hence their domains of validity, in contrast to

theories in some other areas of human thought.

Einstein’s theory is now crying out

The theory of gravity is also notoriously nonrenormalizable. Simply comparing Newton’s

law V(r)= G

/r with Coulomb’s V(r)= α/r we see that Newton’s gravitational

constant G

has mass dimension −2. No more need be said. We come to the same

morose conclusion that the theory of gravity, just like Fermi’s theory of weak interaction,

is nonrenormalizable. To repeat the argument, if we calculate graviton-graviton scattering

at energy E, we encounter the series ∼ [1 + G

+ (G

)

...

Just as in our discussion of the Fermi theory, the nonrenormalizability of quantum grav-

ity tells us that at the Planck energy scale (1/G

)

≡ M

Planck

∼ 10

proton

new physics

must appear. Fermi’s theory cried out, and the new physics turned out to be the elec-

troweak theory. Einstein’s theory is now crying out. Will the new physics turn out to be

string theory?

Exercise

III.2.1 Consider the d-dimensional scalar field theory S =



(∂ϕ)

+ λϕ

...

+ λ

...

Show that [ϕ] = (d − 2)/2 and [λ

] = n(2 − d)/2 +d. Note that ϕ is dimensionless for d =2.

J. Polchinski, String Theory.

III.3 Counterterms and Physical Perturbation Theory

Renormalizability

The heuristic argument of the previous chapter indicates that theories whose coupling has

negative mass dimension are nonrenormalizable. What about theories with dimensionless

couplings, such as quantum electrodynamics and the ϕ

theory? As a matter of fact, both

of these theories have been proved to be renormalizable. But it is much more difficult to

prove that a theory is renormalizable than to prove that it is nonrenormalizable. Indeed,

the proof that nonabelian gauge theory (about which more later) is renormalizable took

the efforts of many eminent physicists, culminating in the work of ’t Hooft, Veltman, B.

Lee, Zinn-Justin, and many others.

Consider again the simple ϕ

theory. First, a trivial remark: The physical coupling

constant λ

is a function of s

, t

, and u

[see (III.1.4)]. For theoretical purposes it is much

less cumbersome to set s

, t

, and u

equal to μ

and thus use, instead of (III.1.4), the

simpler definition

−iλ

=−iλ + 3iCλ

log







+ O(λ

) (1)

This is purely for theoretical convenience.

We saw that to order λ

the meson-meson scattering amplitude when expressed in terms

of the physical coupling λ

is independent of the cutoff . How do we prove that this is true

to all orders in λ? Dimensional analysis only tells us that to any order in λ the dependence of

the meson scattering amplitude on the cutoff must be a sum of terms going as [log(/μ)]

with some power p.

The meson-meson scattering amplitude is certainly not the only quantity that depends

on the cutoff. Consider the inverse of the ϕ propagator to order λ

as shown in figure III.3.1.

In fact, the kinematic point s

= t

= u

= μ

cannot be reached experimentally, but that’s of concern to

theorists.

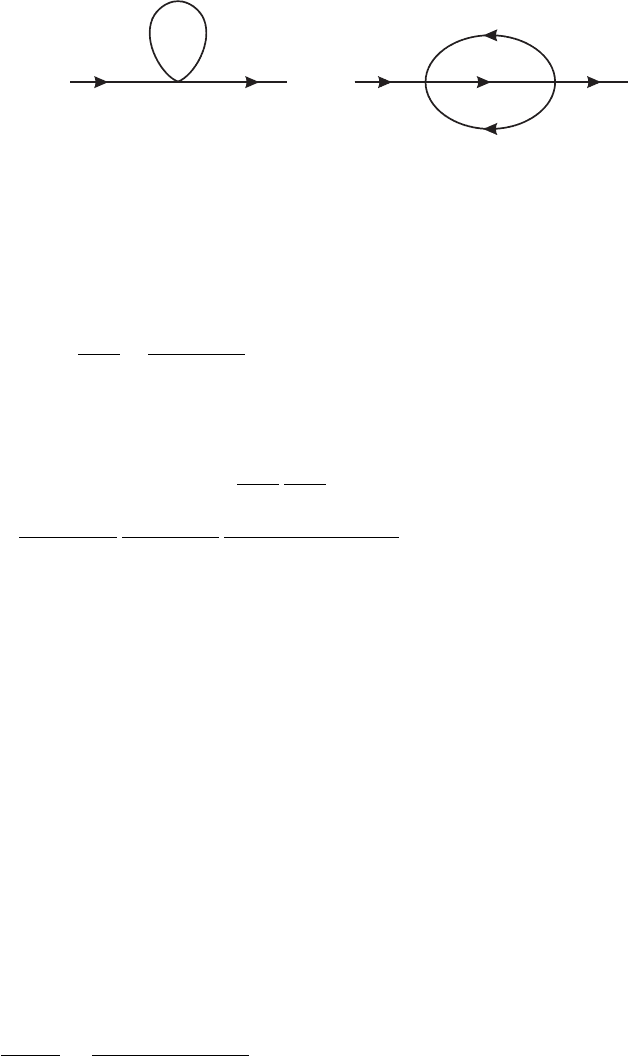
174 | III. Renormalization and Gauge Invariance

(a) (b)

Figure III.3.1

The Feynman diagram in figure III.3.1a gives something like

−iλ







(2π)



− m

+ iε



The precise value does not concern us; we merely note that it depends quadratically on the

cutoff  but not on k

. The diagram in figure III.3.1b involves a double integral

I(k, m, ; λ) ≡ (−iλ)









(2π)

− m

+ iε

− m

+ iε

(p + q + k)

− m

+ iε

(2)

Counting powers of p and q we see that the integral ∼



P/P

) and so I depends

quadratically on the cutoff .

By Lorentz invariance I is a function of k

, which we can expand in a series D + Ek

...

. The quantity D is just I with the external momentum k set equal to zero and

so depends quadratically on the cutoff . Next, we can obtain E by differentiating I with

respect to k twice and then setting k equal to zero. This clearly decreases the powers of p and

q in the integrand by 2 and so E depends only logarithmically on the cutoff . Similarly,

we can obtain F by differentiating I with respect to k four times and then setting k equal to

zero. This decreases the powers of p and q in the integrand by 4 and thus F is given by an

integral that goes as ∼



P/P

for large P . The integral is convergent and hence cutoff

independent. We can clearly repeat the argument ad infinitum. Thus F and the terms in

(

...

) are cutoff independent as the cutoff goes to infinity and we don’t have to worry about

them.

Putting it altogether, we have the inverse propagator k

−m

+a +bk

up to O(k

) with

a and b, respectively, quadratically and logarithmically cutoff dependent. The propagator

is changed to

− m

→

(1 + b)k

− (m

− a)

(3)

The pole in k

is shifted to m

≡ m

+ δm

≡ (m

− a)(1 + b)

−1

, which we identify as

the physical mass. This shift is known as mass renormalization. Physically, it is quite

reasonable that quantum fluctuations will shift the mass.

III.3. Physical Perturbation Theory | 175

What about the fact that the residue of the pole in the propagator is no longer 1 but

(1 + b)

−1

To understand this shift in the residue, recall that we blithely normalized the field ϕ so

that L =

(∂ϕ)

...

. That the coefficient of k

in the lowest order inverse propagator

− m

is equal to 1 reflects the fact that the coefficient of

(∂ϕ)

in L is equal to 1.

There is certainly no guarantee that with higher order corrections included the coefficient

(∂ϕ)

in an effective L will stay at 1. Indeed, we see that it is shifted to (1 + b).For

historical reasons, this is known as “wave function renormalization” even though there is

no wave function anywhere in sight. A more modern term would be field renormalization.

(The word renormalization makes some sense in this case, as we did normalize the field

without thinking too much about it.)

Incidentally, it is much easier to say “logarithmic divergent” than to say “logarithmically

dependent on the cutoff ,” so we will often slip into this more historical and less accurate

jargon and use the word divergent. In ϕ

theory, the wave function renormalization and the

coupling renormalization are logarithmically divergent, while the mass renormalization

is quadratically divergent.

Bare versus physical perturbation theory

What we have been doing thus far is known as bare perturbation theory. We should have

put the subscript 0 on what we have been calling ϕ, m, and λ. The field ϕ

is known as

the bare field, and m

and λ

are known as the bare mass and bare coupling, respectively.

I did not put on the subscript 0 way back in part I because I did not want to clutter up the

notation before you, the student, even knew what a field was.

Seen in this light, using bare perturbation theory seems like a really stupid thing to

do, and it is. Shouldn’t we start out with a zeroth order theory already written in terms of

the physical mass m

and physical coupling λ

that experimentalists actually measure,

and perturb around that theory? Yes, indeed, and this way of calculating is known as

renormalized or dressed perturbation theory, or as I prefer to call it, physical perturbation

theory.

We write

L =

[(∂ϕ)

− m

] −

+ A(∂ϕ)

+ Bϕ

+ Cϕ

(4)

(A word on notation: The pedantic would probably want to put a subscript P on the field

ϕ, but let us clutter up the notation as little as possible.) Physical perturbation theory

works as follows. The Feynman rules are as before, but with the crucial difference that

for the coupling we use λ

and for the propagator we write i/(k

− m

+ iε) with the

physical mass already in place. The last three terms in (4) are known as counterterms.

The coefficients A, B , and C are determined iteratively (see later) as we go to higher and

higher order in perturbation theory. They are represented as crosses in Feynman diagrams,

as indicated in figure III.3.2, with the corresponding Feynman rules. All momentum

integrals are cut off.

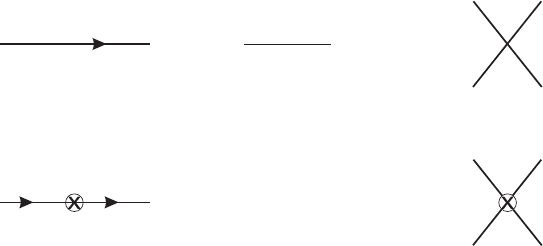
176 | III. Renormalization and Gauge Invariance

+2i(Ak

+ B)

−m

−iλ

4!iC

Figure III.3.2

Let me now explain how A, B , and C are determined iteratively. Suppose we have

determined them to order λ

. Call their values to this order A

N ,

and C

. Draw all the

diagrams that appear in order λ

N+1

. We determine A

N+1,

and C

N+1

by requiring

that the propagator calculated to the order λ

N+1

has a pole at m

with a residue equal to

1, and that the meson-meson scattering amplitude evaluated at some specified values of

the kinematic variables has the value −iλ

. In other words, the counterterms are fixed

by the condition that m

and λ

are what we say they are. Of course, A, B , and C will

be cutoff dependent. Note that there are precisely three conditions to determine the three

unknowns A

N+1,

and C

N+1

Explained in this way, you can see that it is almost obvious that physical perturbation

theory works, that is, it works in the sense that all the physical quantities that we calculate

will be cutoff independent. Imagine, for example, that you labor long and hard to calculate

the meson-meson scattering amplitude to order λ

. It would contain some cutoff depen-

dent and some cutoff independent terms. Then you simply add a contribution given by

and adjust C

to cancel the cutoff dependent terms.

But ah, you start to worry. You say, “What if I calculate the amplitude for two mesons to

go into four mesons, that is, diagrams with six external legs? If I get a cutoff dependent

answer, then I am up the creek, as there is no counterterm of the form Dϕ

in (4) to soak

up the cutoff dependence.” Very astute of you, but this worry is covered by the following

power counting theorem.

Degree of divergence

Consider a diagram with B

external ϕ lines. First, a definition: A diagram is said to have

a superficial degree of divergence D if it diverges as 

. (A logarithmic divergence log 

counts as D = 0.) The theorem says that D is given by

D = 4 − B

(5)

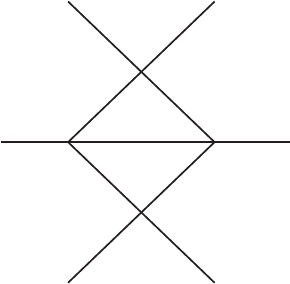
III.3. Physical Perturbation Theory | 177

Figure III.3.3

I will give a proof later, but I will first illustrate what (5) means. For the inverse propagator,

which has B

=2, we are told that D = 2. Indeed, we encountered a quadratic divergence.

For the meson-meson scattering amplitude, B

= 4, and so D = 0, and indeed, it is

logarithmically divergent.

According to the theorem, if you calculate a diagram with six external legs (what is

technically sometimes known as the six-point function), B

=6 and D =−2. The theorem

says that your diagram is convergent or cutoff independent (i.e., the cutoff dependence

disappears as 

−2

). You didn’t have to worry. You should draw a few diagrams to check

this point. Diagrams with more external legs are even more convergent.

The proof of the theorem follows from simple power counting. In addition to B

and

D, let us define B

as the number of internal lines, V as the number of vertices, and L

as the number of loops. (It is helpful to focus on a specific diagram such as the one in

figure III.3.3 with B

= 6, D =−2, B

= 5, V = 4, and L = 2.)

The number of loops is just the number of



k/(2π)

] we have to do. Each internal

line carries with it a momentum to be integrated over, so we seem to have B

integrals to

do. But the actual number of integrals to be done is of course decreased by the momentum

conservation delta functions associated with the vertices, one to each vertex. There are thus

V delta functions, but one of them is associated with overall momentum conservation of

the entire diagram. Thus, the number of loops is

L = B

− (V − 1) (6)

[If you have trouble following this argument, you should work things out for the diagram

in figure III.3.3 for which this equation reads 2 = 5 − (4 − 1).]

For each vertex there are four lines coming out (or going in, depending on how you look

at it). Each external line comes out of (or goes into) one vertex. Each internal line connects

two vertices. Thus,

4V = B

+ 2B

(7)

(For figure III.3.3 this reads 4

4 = 6 + 2

5.)

178 | III. Renormalization and Gauge Invariance

Finally, for each loop there is a



k while for each internal line there is a

i/(k

− m

+ iε), bringing the powers of momentum down by 2. Hence,

D = 4L − 2B

(8)

(For figure III.3.3 this reads −2 = 4

2 − 2

5.)

Putting (6), (7), and (8) together, we obtain the theorem (5).

As you can plainly see, this

formalizes the power counting we have been doing all along.

Degree of divergence with fermions

To test if you understood the reasoning leading to (5), consider the Yukawa theory we met

in (II.5.19). (We suppress the counterterms for typographical clarity.)

L =

ψ(iγ

∂

− m

)ψ +

[(∂ϕ)

− μ

] −λ

+ f

ψψ (9)

Now we have to count F

and F

, the number of internal and external fermion lines,

respectively, and keep track of V

and V

, the number of vertices with the coupling f and

λ, respectively. We have five equations altogether. For instance, (7) splits into two equations

because we now have to count fermion lines as well as boson lines. For example, we now

have

+ 4V

= B

+ 2B

(10)

We (that is, you) finally obtain

D = 4 − B

−

(11)

So the divergent amplitudes, that is, those classes of diagrams with D ≥0, have (B

, F

) =

(0, 2), (2, 0), (1, 2), and (4, 0). We see that these correspond to precisely the six terms in

the Lagrangian (9), and thus we need six counterterms.

Note that this counting of superficial powers of divergence shows that all terms with

mass dimension ≤4 are generated. For example, suppose that in writing down the La-

grangian (9) we forgot to include the λ

term. The theory would demand that we include

this term: We have to introduce it as a counterterm [the term with (B

, F

) = (4, 0) in the

list above].

A common feature of (5) and (11) is that they both depend only on the number of external

lines and not on the number of vertices V . Thus, for a given number of external lines, no

matter to what order of perturbation theory we go, the superficial degree of divergence

remains the same. Further thought reveals that we are merely formalizing the dimension-

counting argument of the preceding chapter. [Recall that the mass dimension of a Bose

field [ϕ] is 1 and of a Fermi field [ψ]is

. Hence the coefficients 1 and

in (11).]

The superficial degree of divergence measures the divergence of the Feynman diagram as all internal

momenta are scaled uniformly by k → ak with a tending to infinity. In a more rigorous treatment we have to

worry about the momenta in some subdiagram (a piece of the full diagram) going to infinity with other momenta

held fixed.

III.3. Physical Perturbation Theory | 179

Our discussion hardly amounts to a rigorous proof that theories such as the Yukawa

theory are renormalizable. If you demand rigor, you should consult the many field theory

tomes on renormalization theory, and I do mean tomes, in which such arcane topics as

overlapping divergences and Zimmerman’s forest formula are discussed in exhaustive and

exhausting detail.

Nonrenormalizable field theories

It is instructive to see how nonrenormalizable theories reveal their unpleasant personali-

ties when viewed in the context of this discussion. Consider the Fermi theory of the weak

interaction written in a simplified form:

L =

ψ(iγ

∂

− m

)ψ +G(

ψψ)

The analogs of (6), (7), and (8) now read L = F

− (V − 1),4V = F

+ 2F

, and D =

4L − F

. Solving for the superficial degree of divergence in terms of the external number

of fermion lines, we find

D = 4 −

+ 2V (12)

Compared to the corresponding equations for renormalizable theories (5) and (11), D

now depends on V . Thus if we calculate fermion-fermion scattering (F

=4), for example,

the divergence gets worse and worse as we go to higher and higher order in the perturbation

series. This confirms the discussion of the previous chapter. But the really bad news is

that for any F

, we would start running into divergent diagrams when V gets sufficiently

large, so we would have to include an unending stream of counterterms (

ψψ)

, (

ψψ)

(

ψψ)

...

, each with an arbitrary coupling constant to be determined by an experimental

measurement. The theory is severely limited in predictive power.

At one time nonrenormalizable theories were considered hopeless, but they are accepted

in the modern view based on the effective field theory approach, which I will discuss in

chapter VIII.3.

Dependence on dimension

The superficial degree of divergence clearly depends on the dimension d of spacetime since

each loop is associated with



k. For example, consider the Fermi interaction G(

ψψ)

(1 + 1)-dimensional spacetime. Of the three equations that went into (12) one is changed

to D = 2L − F

, giving

D = 2 −

(13)

the analog of (12) for 2-dimensional spacetime. In contrast to (12), V no longer enters, and

the only superficial diagrams have F

= 2 and 4, which we can cancel by the appropriate

180 | III. Renormalization and Gauge Invariance

counterterms. The Fermi interaction is renormalizable in (1 +1)-dimensional spacetime.

I will come back to it in chapter VII.4.

The Weisskopf phenomenon

I conclude by pointing out that the mass correction to a Bose field and to a Fermi field

diverge differently. Since this phenomenon was first discovered by Weisskopf, I refer to

it as the Weisskopf phenomenon. To see this go back to (11) and observe that B

and F

contribute differently to the superficial degree of divergence D.ForB

= 2, F

= 0, we

have D = 2, and thus the mass correction to a Bose field diverges quadratically, as we have

already seen explicitly [the quantity a in (3)]. But for F

= 2, B

= 0, we have D = 1 and

it looks like the fermion mass is linearly divergent. Actually, in 4-dimensional field theory

we cannot possibly get a linear dependence on the cutoff. To see this, it is easiest to look at,

as an example, the Feynman integral you wrote down for exercise II.5.1, for the diagram

in figure II.5.1:

(if )



(2π)

− μ

p+  k + m

(p + k)

− m

≡ A(p

) p + B(p

) (14)

where I define the two unknown functions A(p

) and B(p

) for convenience. (For the

purpose of this discussion it doesn’t matter whether we are doing bare or physical pertur-

bation theory. If the latter, then I have suppressed the subscript P for the sake of notational

clarity.)

Look at the integrand for large k. You see that the integral goes as





k( k/k

) and

looks linearly divergent, but by reflection symmetry k →−k the integral to leading order

vanishes. The integral in (14) is merely logarithmically divergent. The superficial degree

of divergence D often gives an exaggerated estimate of how bad the divergence can be

(hence the adjective “superficial”). In fact, staring at (14) we can prove more, for instance,

that B(p

) must be proportional to m. As an exercise you can show, using the Feynman

rules given in chapter II.5, that the same conclusion holds in quantum electrodynamics.

For a boson, quantum fluctuations give δμ ∝ 

/μ, while for a fermion such as the

electron, quantum correction to its mass δm ∝ m log(/m) is much more benign. It is

interesting to note that in the early twentieth century physicists thought of the electron

as a ball of charge of radius a. The electrostatic energy of such a ball, of the order e

/a,

was identified as the electron mass. Interpreting 1/a as , we could say that in classical

physics the electron mass is proportional to  and diverges linearly. Thus, one way of

stating the Weisskopf phenomenon is that “bosons behave worse than a classical charge,

but fermions behave better.”

As Weisskopf explained in 1939, the difference in the degree of the divergence can be

understood heuristically in terms of quantum statistics. The “bad” behavior of bosons has

to do with their gregariousness. A fermion would push away the virtual fermions fluctuat-

ing in the vacuum, thus creating a cavity in the vacuum charge distribution surrounding

III.3. Physical Perturbation Theory | 181

it. Hence its self-energy is less singular than would be the case were quantum statistics

not taken into account. A boson does the opposite.

The “bad” behavior of bosons will come back to haunt us later.

Power of  counts the number of loops

This is a convenient place to make a useful observation, though unrelated to divergences

and cut-off dependence. Suppose we restore Planck’s unit of action . In the path integral,

the integrand becomes e

iS/

(recall chapter I.2) so that effectively L → L/. Consider

L =−

ϕ(∂

)ϕ −

, just to be definite. The coupling λ → λ/, so that each vertex

is now associated with a factor of 1/. Recall that the propagator is essentially the inverse

of the operator (∂

+ m

), and so in momentum space 1/(k

− m

) → /(k

− m

). Thus

the powers of  are given by the number of internal lines minus the number of vertices

P = B

−V =L − 1, where we used (6). You can check that this holds in general and not

just for ϕ

theory.

This observation shows that organizing Feynman diagrams by the number of loops

amounts to an expansion in Planck’s constant (sometimes called a semi-classical expan-

sion), with the tree diagrams providing the leading term. We will come across this again

in chapter IV.3.

Exercises

III.3.1 Show that in (1 + 1)-dimensional spacetime the Dirac field ψ has mass dimension

, and hence the

Fermi coupling is dimensionless.

III.3.2 Derive (11) and (13).

III.3.3 Show that B(p

) in (14) vanishes when we set m = 0. Show that the same behavior holds in quantum

electrodynamics.

III.3.4 We showed that the specific contribution (14) to δm is logarithmically divergent. Convince yourself that

this is actually true to any finite order in perturbation theory.

III.3.5 Show that the result P = L − 1 holds for all the theories we have studied.