Zee A. Quantum Field Theory in a Nutshell
Подождите немного. Документ загружается.


202 | III. Renormalization and Gauge Invariance
The residue of the pole in iD
P
μν
(q) is the physical or renormalized charge squared:
e
2
R
= e
2
1
1 + e
2
(0)
(5)
Respect for gauge invariance
In order to determine e
R
in terms of e, let us calculate to lowest order
i
μν
(q) = (−)
d
4
p
(2π)
4
tr
iγ
ν
i
p + q −m
iγ
μ
i
p − m
(6)
For large p the integrand goes as 1/p
2
with a subleading term going as m
2
/p
4
causing
the integral to have a quadratically divergent and a logarithmically divergent piece. (You
see, it is easy to slip into bad language.) Not a conceptual problem at all, as I explained
in chapter III.1. We simply regularize. But now there is a delicate point: Since gauge
invariance plays a crucial role, we must make sure that our regularization respects gauge
invariance.
In the Pauli-Villars regularization (III.1.13) we replace (6) by
i
μν
(q) = (−)
d
4
p
(2π)
4
tr
iγ
ν
i
p + q −m
iγ
μ
i
p − m
−
a
c
a
tr
iγ
ν
i
p + q −m
a
iγ
μ
i
p − m
a
(7)
Now the integrand goes as (1 −
a
c
a
)(1/p
2
) with a subleading term going as (m
2
−
a
c
a
m
2
a
)(1/p
4
), and thus the integral would converge if we choose c
a
and m
a
such that
a
c
a
= 1 (8)
and
a
c
a
m
2
a
= m
2
(9)
Clearly, we have to introduce at least two regulator masses. We are confessing to ignorance
of the physics above the mass scale m
a
. The integral in (7) is effectively cut off when the
momentum p exceeds m
a
.
Does a bell ring for you? It should, as this discussion conceptually parallels that in the
appendix to chapter I.9.
The gauge invariant form (3) we expect to get actually suggests that we need fewer
regulator terms than we think. Imagine expanding (6) in powers of q. Since
μν
(q) = (q
μ
q
ν
− g
μν
q
2
)[(0) +
...
]
we are only interested in terms of O(q
2
) and higher in the Feynman integral. If we expand
the integrand in (6), we see that the term of O(q
2
) goes as 1/p
4
for large p, thus giving a
logarithmically divergent (speaking bad language again!) contribution. (Incidentally, you
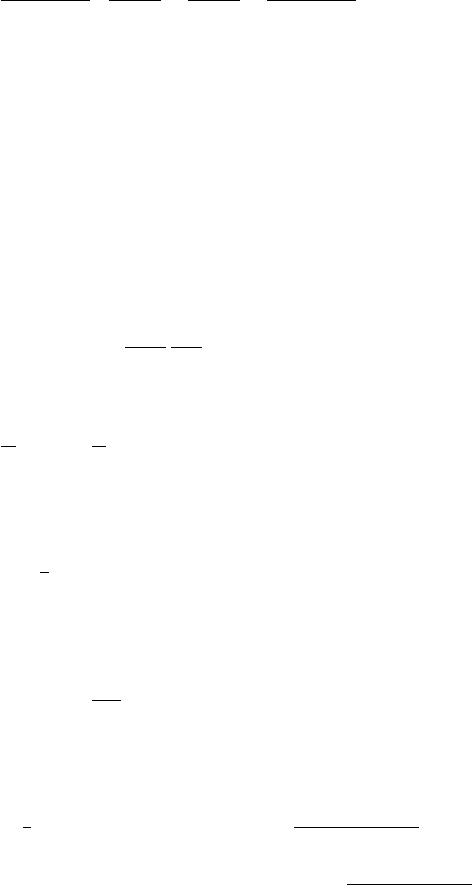
III.7. Polarizing the Vacuum | 203
may recall that this sort of argument was also used in chapter III.3.) It seems that we need
only one regulator. This argument is not rigorous because we have not proved that (q
2
)
has a power series expansion in q
2
, but instead of worrying about it let us proceed with
the calculation.
Once the integral is convergent, the proof of gauge invariance given in chapter II.7 now
goes through. Let us recall briefly how the proof went. In computing q
μ
μν
(q) we use the
identity
1
p + q −m
q
1
p − m
=
1
p − m
−
1
p + q −m
to split the integrand into two pieces that cancel upon shifting the integration variable
p → p + q. Recall from exercise (II.7.2) that we were concerned that in some cases the
shift may not be allowed, but it is allowed if the integral is sufficiently convergent, as is
indeed the case now that we have regularized. In any event, the proof is in the eating of
the pudding, and we will see by explicit calculation that
μν
(q) indeed has the form in (3).
Having learned various computational tricks in the previous chapter you are now ready
to tackle the calculation. I will help by walking you through it. In order not to clutter up
the page I will suppress the regulator terms in (7) in the intermediate steps and restore
them toward the end. After a few steps you should obtain
i
μν
(q) =−
d
4
p
(2π)
4
N
μν
D
where N
μν
= tr[γ
ν
( p + q + m)γ
μ
( p + m)] and
1
D
=
1
0
dα
1
D
with D = [l
2
+ α(1 − α)q
2
− m
2
+ iε]
2
, where l = p + αq. Eliminating p in favor of l and
beating on N
μν
you will find that N
μν
is effectively equal to
−4
1
2
g
μν
l
2
+ α(1 − α)(2q
μ
q
ν
− g
μν
q
2
) − m
2
g
μν
Integrate over l using (D.12) and (D.13) and, writing the contribution from the regulators
explicitly, obtain
μν
(q) =−
1
4π
2
1
0
dα
F
μν
(m) −
a
c
a
F
μν
(m
a
)
(10)
where
F
μν
(m)
=
1
2
g
μν
2
− 2[m
2
− α(1 − α)q
2
] log
2
m
2
− α(1 − α)q
2
+ m
2
− α(1 − α)q
2
− [α(1 − α)(2q
μ
q
ν
− g
μν
q
2
) − m
2
g
μν
]
log
2
m
2
− α(1 − α)q
2
− 1
(11)
Remember, you are doing the calculation; I am just pointing the way. In appendix D, was
introduced to give meaning to various divergent integrals. Since our integral is convergent,

204 | III. Renormalization and Gauge Invariance
we should not need , and indeed, it is gratifying to see that in (10) drops out thanks
to the conditions (8) and (9). Some other terms drop out as well, and we end up with
μν
(q) =−
1
2π
2
(q
μ
q
ν
− g
μν
q
2
)
1
0
dα α(1 − α)
{log[m
2
− α(1 − α)q
2
] −
a
c
a
log[m
2
a
− α(1 − α)q
2
]} (12)
Lo and behold! The vacuum polarization tensor indeed has the form
μν
(q) = (q
μ
q
ν
−
g
μν
q
2
)(q
2
). Our regularization scheme does respect gauge invariance.
For q
2
m
2
a
(the kinematic regime we are interested in had better be much lower than
our threshold of ignorance) we simply define log M
2
≡
a
c
a
log m
2
a
in (12) and obtain
(q
2
) =
1
2π
2
1
0
dα α(1 − α) log
M
2
m
2
− α(1 − α)q
2
(13)
Note that our heuristic argument is indeed correct. In the end, effectively we need only
one regulator, but in the intermediate steps we needed two. Actually, this bickering over
the number of regulators is beside the point.
In chapter III.1 I mentioned dimensional regularization as an alternative to Pauli-Villars
regularization. Historically, dimensional regularization was invented to preserve gauge
invariance in nonabelian gauge theories (which I will discuss in a later chapter). It is
instructive to calculate using dimensional regularization (exercise III.7.1).
Electric charge
Physically, we end up with a result for (q
2
) containing a parameter M
2
expressing our
threshold of ignorance. We conclude that
e
2
R
= e
2
1
1 + (e
2
/12π
2
) log(M
2
/m
2
)
e
2
1 −
e
2
12π
2
log
M
2
m
2
(14)
Quantum fluctuations effectively diminish the charge. I will explain the physical origin of
this effect in a later chapter on renormalization group flow.
You might argue that physically charge is measured by how strongly one electron scatters
off another electron. To order e
4
, in addition to the diagrams in chapter II.7, we also have,
among others, the diagrams shown in figure III.7.4a,b,c. We have computed 4a, but what
about 4b and 4c? In many texts, it is shown that contributions of III.7.4b and III.7.4c to
charge renormalization cancel. The advantage of using the Lagrangian in (1) is that this
fact becomes self-evident: Charge is a measure of how the photon propagates.
To belabor a more or less self-evident point let us imagine doing physical or renormalized
perturbation theory as explained in chapter III.3. The Lagrangian is written in terms of
physical or renormalized fields (and as before we drop the subscript P on the fields)
L =
¯
ψ(iγ
μ
(∂
μ
− iA
μ
) − m
P
)ψ −
1
4e
2
P
F
μν
F
μν
+ A
¯
ψiγ
μ
(∂
μ
− iA
μ
)ψ +B
¯
ψψ − CF
μν
F
μν
(15)
III.7. Polarizing the Vacuum | 205
+
(a) (b) (c)
Figure III.7.4
where the coefficients of the counterterms A, B , and C are determined iteratively. The
point is that gauge invariance guarantees that
¯
ψiγ
μ
∂
μ
ψ and
¯
ψγ
μ
A
μ
ψ always occur in
the combination
¯
ψiγ
μ
(∂
μ
− iA
μ
)ψ: The strength of the coupling of A
μ
to
¯
ψγ
μ
ψ cannot
change. What can change is the ease with which the photon propagates through spacetime.
This statement has profound physical implications. Experimentally, it is known to a
high degree of accuracy that the charges of the electron and the proton are opposite and
exactly equal. If the charges were not exactly equal, there would be a residual electrostatic
force between macroscopic objects. Suppose we discovered a principle that tells us that
the bare charges of the electron and the proton are exactly equal (indeed, as we will see,
in grand unification theories, this fact follows from group theory). How do we know
that quantum fluctuations would not make the charges slightly unequal? After all, the
proton participates in the strong interaction and the electron does not and thus many
more diagrams would contribute to the long range electromagnetic scattering between
two protons. The discussion here makes clear that this equality will be maintained for the
obvious reason that charge renormalization has to do with the photon. In the end, it is all
due to gauge invariance.
Modifying the Coulomb potential
We have focused on charge renormalization, which is determined completely by (0), but
in (13) we obtained the complete function (q
2
), which tells us how the q dependence of
the photon propagator is modified. According to the discussion in chapter I.5, the Coulomb
potential is just the Fourier transform of the photon propagator (see also exercise III.5.3).
Thus, the Coulomb interaction is modified from the venerable 1/r law at a distance scale
of the order of (2m)
−1
, namely the inverse of the characteristic value of q in (q
2
). This
modification was experimentally verified as part of the Lamb shift in atomic spectroscopy,
another great triumph of quantum electrodynamics.
206 | III. Renormalization and Gauge Invariance
Exercises
III.7.1 Calculate
μν
(q) using dimensional regularization. The procedure is to start with (6), evaluate the trace
in N
μν
, shift the integration momentum from p to l, and so forth, proceeding exactly as in the text,
until you have to integrate over the loop momentum l. At that point you “pretend” that you are living
in d-dimensional spacetime, so that the term like l
μ
l
ν
in N
μν
, for example, is to be effectively replaced
by (1/d)g
μν
l
2
. The integration is to be performed using (III.1.15) and various generalizations thereof.
Show that the form (3) automatically emerges when you continue to d =4.
III.7.2 Study the modified Coulomb’s law as determined by the Fourier integral
d
3
q{1/q
2
[1 + e
2
(q
2
)]}e
i q x
.

III.8 Becoming Imaginary and Conserving Probability
When Feynman amplitudes go imaginary
Let us admire the polarized vacuum, viz (III.7.13):
(q
2
) =
1
2π
2
1
0
dαα(1 − α) log
2
m
2
− α(1 − α)q
2
− iε
(1)
Dear reader, you have come a long way in quantum field theory, to be able to calculate such
an amazing effect. Quantum fluctuations alter the way a photon propagates!
For a spacelike photon, with q
2
negative, is real and positive for momentum small
compared to the threshold of our ignorance . For a timelike photon, we see that if q
2
> 0
is large enough, the argument of the logarithm may go negative, and thus becomes
complex. As you know, the logarithmic function log z could be defined in the complex
z plane with a cut that can be taken conventionally to go along the negative real axis,
so that for w real and positive, log(−w ± iε) = log(w) ± iπ [since in polar coordinates
log(ρe
iθ
) = log(ρ) + iθ].
We now invite ourselves to define a function in the complex plane: (z) ≡
1/(2π
2
)
1
0
dαα(1 − α) log
2
/(m
2
− α(1 − α)z). The integrand has a cut on the positive
real z axis extending from z = m
2
/(α(1 − α)) to infinity (fig. III.8.1). Since the maximum
value of α(1 − α) in the integration range is
1
4
, (z) is an analytic function in the complex
z plane with a cut along the real axis starting at z
c
= 4m
2
. The integral over α smears all
those cuts of the integrand into one single cut.
For timelike photons with large enough q
2
, a mathematician might be paralyzed won-
dering which side of the cut to go to, but we as physicists know, as per the iε prescription
from chapter I.3, that we should approach the cut from above, namely that we should take
(q
2
+ iε) (with ε, as always, a positive infinitesimal) as the physical value. Ultimately,
causality tells us which side of the cut we should be on.
That the imaginary part of starts at
q
2
> 2m provides a strong hint of the physics
behind amplitudes going complex. We began the preceding chapter talking about how
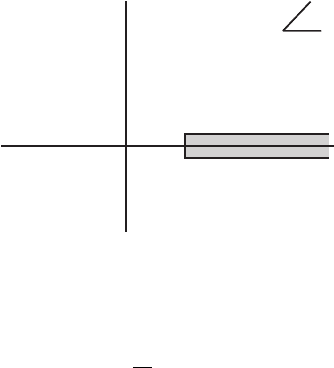
208 | III. Renormalization and Gauge Invariance
z
4m
2
Figure III.8.1
a photon merrily propagating along could always metamorphose into a virtual electron-
positron pair that, after a short time dictated by the uncertainly principle, annihilate each
other to become a photon again. For
q
2
> 2m the pair is no longer condemned to be
virtual and to fluctuate out of existence almost immediately. The pair has enough energy
to get real. (If you did the exercises religiously, you would recognize that these points were
already developed in exercises I.7.4 and III.1.2.)
Physically, we could argue more forcefully as follows. Imagine a gauge boson of mass M
coupling to electrons just like the photon. (Indeed, in this book we started out supposing
that the photon has a mass.) The vacuum polarization diagram then provides a one-loop
correction to the vector boson propagator. For M>2m, the vector boson becomes unstable
against decay into an electron-positron pair. At the same time, acquires an imaginary
part. You might suspect that Im might have something to do with the decay rate. We will
verify these suspicions later and show that, hey, your physical intuition is pretty good.
When we ended the preceding chapter talking about the modifications to the Coulomb
potential, we thought of a spacelike virtual photon being exchanged between two charges as
in electron-electron or electron-proton scattering (chapter II.6). Use crossing (chapter II.8)
to map electron-electron scattering into electron-positron scattering. The vacuum polariza-
tion diagram then appears (fig. III.8.2) as a correction to electron-positron scattering. One
function covers two different physical situations.
Incidentally, the title of this section should, strictly speaking, have the word “complex,”
but it is more dramatic to say “When Feynman amplitudes go imaginary,” if only to echo
certain movie titles.
Dispersion relations and high frequency behavior
One of the most remarkable discoveries in elementary
particle physics has been that of the existence of the
complex plane.
—J. Schwinger
Considering that amplitudes are calculated in quantum field theory as integrals over
products of propagators, it is more or less clear that amplitudes are analytic functions

III.8. Becoming Imaginary | 209
e
⫹
e
⫺
e
⫹
e
⫺
Figure III.8.2
of the external kinematic variables. Another example is the scattering amplitude M in
chapter III.1: it is manifestly an analytic function of s, t , and u with various cuts. From the
late 1950s until the early 1960s, considerable effort was devoted to studying analyticity in
quantum field theory, resulting in a vast literature.
Here we merely touch upon some elementary aspects. Let us start with an embarrass-
ingly simple baby example: f(z)=
1
0
dα1/(z − α) = log((z − 1)/z). The integrand has a
pole at z = α, which got smeared by the integral over α into a cut stretching from 0 to 1.
At the level of physicist rigor, we may think of a cut as a lot of poles mashed together and
a pole as an infinitesimally short cut.
We will mostly encounter real analytic functions, namely functions satisfying f
∗
(z) =
f(z
∗
) (such as log z). Furthermore, we focus on functions that have cuts along the real axis,
as exemplified by (z). For the class of analytic functions specified here, the discontinuity
of the function across the cut is given by discf(x)≡ f(x +iε) − f(x− iε) =f(x +iε) −
f(x + iε)
∗
= 2iImf(x + iε). Define, for σ real, ρ(σ) = Imf(σ + iε). Using Cauchy’s
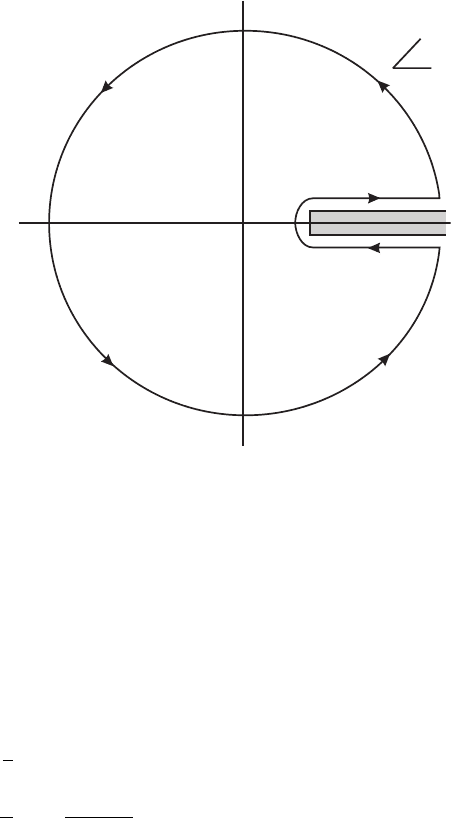
theorem with a contour C that goes around the cut as indicated in figure III.8.3, we could
write
f(z)=
C
dz
2πi
f(z
)
z
− z
. (2)
Assuming that f(z)vanishes faster than 1/z as z →∞, we can drop the contribution from
infinity and write
f(z)=
1
π
dσ
ρ(σ)
σ − z
(3)
where the integral ranges over the cut. Note that we can check this equation using the
identity (I.2.14):
Imf(x + iε) =
1
π
dσρ(σ)Im
1
σ − x − iε
=
1
π
dσρ(σ)πδ(σ − x)
210 | III. Renormalization and Gauge Invariance
z
C
Figure III.8.3
This relation tells us that knowing the imaginary part of f along the cut allows us to
construct f in its entirety, including a fortiori its real part on and away from the cut.
Relations of this type, known collectively as dispersion relations, go back at least to the
work of Kramers and Kr
¨
onig on optics and are enormously useful in many areas of physics.
We will use it in, for example, chapter VII.4.
We implicitly assumed that the integral over σ converges. If not, we can always (formally)
subtract f(0) =
1
π
dσ ρ(σ )/σ from f(z)as given above and write
f(z)= f(0) +
z
π
dσ
ρ(σ)
σ(σ − z)
(4)
The integral over σ now enjoys an additional factor of 1/σ and hence is more convergent.
In this case, to reconstruct f(z), we need, in addition to knowledge of the imaginary part
of f on the cut, an unknown constant f(0). Evidently, we could repeat this process until
we obtain a convergent integral.
A bell rings, and you, the astute reader, see the connection with the renormalization
procedure of introducing counterterms. In the dispersion weltanschauung, divergent
Feynman integrals correspond to integrals over σ that do not converge. Once again,
divergent integrals do not bend real physicists out of shape: we simply admit to ignorance
of the high σ regime.
During the height of the dispersion program, it was jokingly said that particle theorists
either group or disperse, depending on whether you like group theory or complex analysis
better.

III.8. Becoming Imaginary | 211
Imaginary part of Feynman integrals
Going back to the calculation of vacuum polarization in the preceding chapter, we see
that the numerator N
μν
, which comes from the spin of the photon and of the electron,
is irrelevant in determining the analytic structure of the Feynman diagram. It is the
denominator D that counts. Thus, to get at a conceptual understanding of analyticity
in quantum field theory, we could dispense with spins and study the analog of vacuum
polarization in the scalar field theory with the interaction term L = g(η
†
ξ
†
ϕ + h.c.),
introduced in the appendix to chapter II.6. The ϕ propagator is corrected by the analog
of the diagrams in figure III.7.1 to [compare with (4)]
iD
P
(q) =
i
q
2
− M
2
+ i
+
i
q
2
− M
2
+ i
i(q
2
)
i
q
2
− M
2
+ i
+
...
=
i
q
2
− M
2
+ (q
2
) + i
(5)
To order g
2
we have
i(q
2
) = i
4
g
2
d
4
k
(2π)
4
1
k
2
− μ
2
+ iε
1
(q − k)
2
− m
2
+ iε
(6)
As in the preceding chapter we need to regulate the integral, but we will leave that implicit.
Having practiced with the spinful calculation of the preceding chapter, you can now
whiz through this spinless calculation and obtain
(z) =
g
2
16π
2
1
0
dα log
2
αm
2
+ (1 − α)μ
2
− α(1 − α)z
(7)
with some cutoff. (Please do whiz and not imagine that you could whiz.) We use the
same Greek letter and allow the two particles in the loop to have different masses, in
contrast to the situation in quantum electrodynamics.
As before, for z real and negative, the argument of the log is real and positive, and is
real. By the same token, for z real and positive enough, the argument of the log becomes
negative for some value of α, and (z) goes complex. Indeed,
Im(σ + iε) =−
g
2
16π
2
1
0
dα(−π)θ[α(1 − α)σ − αm
2
− (1 − α)μ
2
]
=
g
2
16π
α
+
α
−
dα
=
g
2
16πσ
(σ − (m + μ)
2
)(σ − (m − μ)
2
) (8)
with α
±
the two roots of the quadratic equation obtained by setting the argument of the
step function to zero.
