Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

192 | III. Renormalization and Gauge Invariance

Integrating and defining N ≡



xρ( x , t) = the total number of bosons, we find one of

the most important relations in condensed matter physics

[N , θ] = i (9)

Number is conjugate to phase angle, just as momentum is conjugate to position. Marvel

at the elegance of this! You would learn in a condensed matter course that this fundamental

relation underlies the physics of the Josephson junction.

You may know that a system of bosons with a “hard core” repulsion between them is a

superfluid at zero temperature. In particular, Bogoliubov showed that the system contains

an elementary excitation obeying a linear dispersion relation.

I will discuss superfluidity

in chapter V.1.

In the path integral formalism, going from the complex field ϕ = ϕ

+ iϕ

to ρ and

θ amounts to a change of integration variables, as I remarked back in chapter I.8. In the

canonical formalism, since one deals with operators, one has to tread with somewhat more

finesse.

The sign of repulsion

In the nonrelativistic theory (7) it is clear that the bosons repel each other: Piling particles

into a high density region would cost you an energy density g

. But it is less clear in

the relativistic theory that λ(

†

)

with λ positive corresponds to repulsion. I outline one

method in exercise III.5.3, but here let’s just take a flying heuristic guess. The Hamiltonian

(density) involves the negative of the Lagrangian and hence goes as λ(

†

)

for large 

and would thus be unbounded below for λ<0. We know physically that a free Bose gas

tends to condense and clump, and with an attractive interaction it surely might want to

collapse. We naturally guess that λ>0 corresponds to repulsion.

I next give you a more foolproof method. Using the central identity of quantum field

theory we can rewrite the path integral for the theory in (1) as

Z =



DDσe



x[(∂

†

)(∂)−m



†

+2σ

†

+(1/λ)σ

]

(10)

Condensed matter physicists call the transformation from (1) to the Lagrangian L =

(∂

†

)(∂) − m



†

 + 2σ

†

 + (1/λ)σ

the Hubbard-Stratonovich transformation. In

field theory, a field that does not have kinetic energy, such as σ , is known as an auxiliary field

and can be integrated out in the path integral. When we come to the superfield formalism

in chapter VIII.4, auxiliary fields will play an important role.

Indeed, you might recall from chapter III.2 how a theory with an intermediate vector

boson could generate Fermi’s theory of the weak interaction. The same physics is involved

here: The theory (10) in which the  field is coupled to an “intermediate σ boson” can

generate the theory (1).

For example, L.D. Landau and E. M. Lifschitz, Statisical Physics, p. 238.

III.5. Nonrelativistic Field Theory | 193

If σ were a “normal scalar field” of the type we have studied, that is, if the terms quadratic

in σ in the Lagrangian had the form

(∂σ )

−

, then its propagator would be

i/(k

− M

+ iε). The scattering amplitude between two  bosons would be proportional

to this propagator. We learned in chapter I.4 that the exchange of a scalar field leads to an

attractive force.

But σ is not a normal field as evidenced by the fact that the Lagrangian contains

only the quadratic term +(1/λ)σ

. Thus its propagator is simply i/(1/λ) = iλ, which (for

λ>0) has a sign opposite to the normal propagator evaluated at low-momentum transfer

i/(k

− M

+ iε) −i/M

. We conclude that σ exchange leads to a repulsive force.

Incidentally, this argument also shows that the repulsion is infinitely short ranged, like

a delta function interaction. Normally, as we learned in chapter I.4 the range is determined

by the interplay between the k

and the M

terms. Here the situation is as if the M

term

is infinitely large. We can also argue that the interaction λ(

†

)

involves creating two

bosons and then annihilating them both at the same spacetime point.

Finite density

One final point of physics that people trained as particle physicists do not always remem-

ber: Condensed matter physicists are not interested in empty space, but want to have a

finite density ¯ρ of bosons around. We learned in statistical mechanics to add a chemical

potential term μϕ

†

ϕ to the Lagrangian (6). Up to an irrelevant (in this context!) additive

constant, we can rewrite the resulting Lagrangian as

L = iϕ

†

∂

ϕ −

∂

†

∂

ϕ − g

(ϕ

†

ϕ −¯ρ)

(11)

Amusingly, mass appears in different places in relativistic and nonrelativistic field

theories. To proceed further, I have to develop the concept of spontaneous symmetry

breaking. Thus, adios for now. We will come back to superfluidity in due time.

Exercises

III.5.1 Obtain the Klein-Gordon equation for a particle in an electrostatic potential (such as that of the nucleus)

by the gauge principle of replacing (∂/∂t) in (2) by ∂/∂t − ieA

. Show that in the nonrelativistic limit

this reduces to the Schr

odinger’s equation for a particle in an external potential.

III.5.2 Take the nonrelativistic limit of the Dirac Lagrangian.

III.5.3 Given a field theory we can compute the scattering amplitude of two particles in the nonrelativistic limit.

We then postulate an interaction potential U(x) between the two particles and use nonrelativistic quan-

tum mechanics to calculate the scattering amplitude, for example in Born approximation. Comparing

the two scattering amplitudes we can determine U(x). Derive the Yukawa and the Coulomb potentials

this way. The application of this method to the λ(

†

)

interaction is slightly problematic since the

delta function interaction is a bit singular, but it should be all right for determining whether the force is

repulsive or attractive.

III.6 The Magnetic Moment of the Electron

Dirac’s triumph

I said in the preface that the emphasis in this book is not on computation, but how can I

not tell you about the greatest triumph of quantum field theory?

After Dirac wrote down his equation, the next step was to study how the electron interacts

with the electromagnetic field. According to the gauge principle already used to write

the Schr

odinger’s equation in an electromagnetic field, to obtain the Dirac equation for

an electron in an external electromagnetic field we merely have to replace the ordinary

derivative ∂

by the covariant derivative D

= ∂

− ieA

(iγ

− m)ψ =0 (1)

Recall (II.1.27).

Acting on this equation with (iγ

+ m), we obtain −(γ

+ m

)ψ =0. We

have γ

({γ

, γ

}+[γ

, γ

])D

−iσ

μν

and iσ

μν

(i/2)σ

μν

, D

] = (e/2)σ

μν

. Thus



−

μν

+ m



ψ =0 (2)

Now consider a weak constant magnetic field pointing in the 3rd direction for definite-

ness, weak so that we can ignore the (A

)

term in (D

)

. By gauge invariance, we can

choose A

= 0, A

=−

, and A

(so that F

= ∂

− ∂

= B). As we will

see, this is one calculation in which we really have to keep track of factors of 2. Then

)

= (∂

)

− ie(∂

+ A

∂

) + O(A

)

= (∂

)

− 2

B(x

∂

− x

∂

) + O(A

)



∇

− e



x ×p + O(A

) (3)

Note that we used ∂

∂

=(∂

) +2A

∂

=2A

∂

, where in (∂

) the partial deriva-

tive acts only on A

. You may have recognized



L ≡x ×p as the orbital angular momentum

III.6. Magnetic Moment of Electron | 195

operator. Thus, the orbital angular momentum generates an orbital magnetic moment that

interacts with the magnetic field.

This calculation makes good physical sense. If we were studying the interaction of a

charged scalar field  with an external electromagnetic field we would start with

+ m

) = 0 (4)

obtained by replacing the ordinary derivative in the Klein-Gordon equation by covariant

derivatives. We would then go through the same calculation as in (3). Comparing (4) with

(2) we see that the spin of the electron contributes the additional term (e/2)σ

μν

As in chapter II.1 we write ψ =





in the Dirac basis and focus on φ since in the

nonrelativistic limit it dominates χ . Recall that in that basis σ

= ε

ij k



0 σ



. Thus

(e/2)σ

μν

acting on φ is effectively equal to (e/2)σ

−F

) = (e/2)2σ

B = 2e



since



S = (σ/2). Make sure you understand all the factors of 2! Meanwhile, according to

what I told you in chapter II.1, we should write φ = e

−imt

, where  oscillates much more

slowly than e

−imt

so that (∂

+ m

−imt

  e

−imt

[−2im(∂/∂t)]. Putting it all together,

we have



−2im

∂

∂t

−



∇

− e



(



L + 2





 = 0 (5)

There you have it! As if by magic, Dirac’s equation tells us that a unit of spin angular

momentum interacts with a magnetic field twice as much as a unit of orbital angular

momentum, an observational fact that had puzzled physicists deeply at the time. The

calculation leading to (5) is justly celebrated as one of the greatest in the history of physics.

The story is that Dirac did not do this calculation until a day after he discovered his

equation, so sure was he that the equation had to be right. Another version is that he

dreaded the possibility that the magnetic moment would come out wrong and that Nature

would not take advantage of his beautiful equation.

Another way of seeing that the Dirac equation contains a magnetic moment is by the

Gordon decomposition, the proof of which is given in an exercise:

¯u(p



)γ

u(p) =¯u(p



)





+ p)

iσ

μν



− p)



u(p) (6)

Looking at the interaction with an electromagnetic field ¯u(p



)γ

u(p)A



− p), we see

that the first term in (6) only depends on the momentum (p



+ p)

and would have

been there even if we were treating the interaction of a charged scalar particle with the

electromagnetic field to first order. The second term involves spin and gives the mag-

netic moment. One way of saying this is that ¯u(p



)γ

u(p) contains a magnetic moment

component.

196 | III. Renormalization and Gauge Invariance

The anomalous magnetic moment

With improvements in experimental techniques, it became clear by the late 1940’s that the

magnetic moment of the electron was larger than the value calculated by Dirac by a factor

of 1.00118 ± 0.00003. The challenge to any theory of quantum electrodynamics was to

calculate this so-called anomalous magnetic moment. As you probably know, Schwinger’s

spectacular success in meeting this challenge established the correctness of relativistic

quantum field theory, at least in dealing with electromagnetic phenomena, beyond any

doubt.

Before we plunge into the calculation, note that Lorentz invariance and current conser-

vation tell us (see exercise III.6.3) that the matrix element of the electromagnetic current

must have the form (here |p, s denotes a state with an electron of momentum p and

polarization s)

p



, s



(0) |p, s=¯u(p



, s



)



) +

iσ

μν

)



u(p, s) (7)

where q ≡(p



−p). The functions F

) and F

), about which Lorentz invariance can

tell us nothing, are known as form factors. To leading order in momentum transfer q , (7)

becomes

¯u(p



, s



)





+ p)

(0) +

iσ

μν

(0) + F

(0)]



u(p, s)

by the Gordon decomposition. The coefficient of the first term is the electric charge

observed by experimentalists and is by definition equal to 1. (To see this, think of potential

scattering, for example. See chapter II.6.) Thus F

(0) = 1. The magnetic moment of the

electron is shifted from the Dirac value by a factor 1 + F

(0).

Schwinger’s triumph

Let us now calculate F

(0) to order α = e

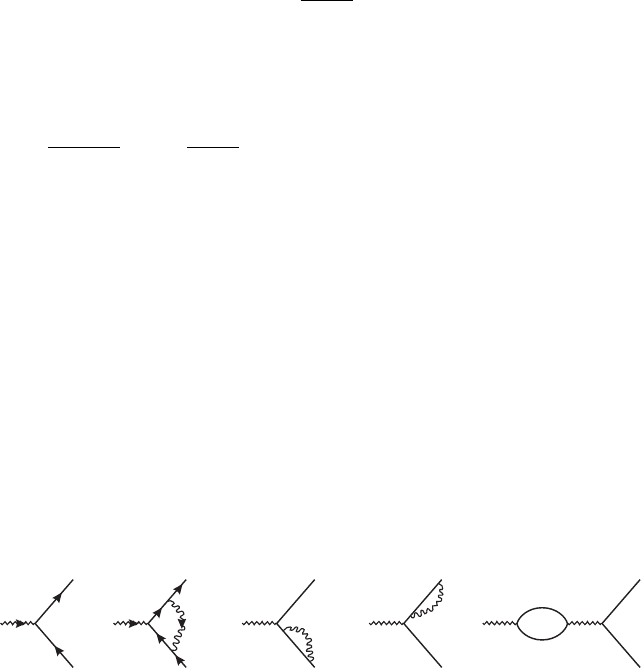
/4π . First draw all the relevant Feynman dia-

grams to this order (fig. III.6.1). Except for figure 1b, all the Feynman diagrams are clearly

proportional to ¯u(p



, s



)γ

u(p, s)and thus contribute to F

), which we don’t care about.

Happy are we! We only have to calculate one Feynman diagram.

p’

p’ + k

p + k

(a) (b) (c) (d) (e)

Figure III.6.1

III.6. Magnetic Moment of Electron | 197

It is convenient to normalize the contribution of figure 1b by comparing it to the lowest

order contribution of figure 1a and write the sum of the two contributions as ¯u(γ

+

)u.

Applying the Feynman rules, we find





(2π)

−i



ieγ

p



+  k − m

p+  k − m

ieγ



(8)

I will now go through the calculation in some detail not only because it is important, but

also because we will be using a variety of neat tricks springing from the brilliant minds of

Schwinger and Feynman. You should verify all the steps of course.

Simplifying somewhat we obtain 

=−ie



k/(2π)

](N

/D), where

= γ

(p



+  k + m)γ

(p+  k + m)γ

(9)

and



+ k)

− m

(p + k)

− m

= 2



dα dβ

. (10)

We have used the identity (D.16). The integral is evaluated over the triangle in the (α-β)

plane bounded by α = 0, β =0, and α + β =1, and

D =[k

+ 2k(αp



+ βp)]

= [l

− (α + β)

]

+ O(q

) (11)

where we completed a square by defining k =l −(αp



+βp). The momentum integration

is now over d

Our strategy is to massage N

into a form consisting of a linear combination of γ

, p

and p

μ

. Invoking the Gordon decomposition (6) we can write (7) as

¯u



) + F

)] −



+ p)

)



Thus, to extract F

(0) we can throw away without ceremony any term proportional to γ

that we encounter while massaging N

. So, let’s proceed.

Eliminating k in favor of l in (9) we obtain

= γ

[ l + P



+ m]γ

[ l + P +m]γ

(12)

where P

μ

≡ (1 − α)p

μ

− βp

and P

≡ (1 − β)p

− αp

μ

. I will use the identities in

appendix D repeatedly, without alerting you every time I use one. It is convenient to

organize the terms in N

by powers of m. (Here I give up writing in complete grammatical

sentences.)

1. The m

term: a γ

term, throw away.

2. The m terms: organize by powers of l. The term linear in l integrates to 0 by symmetry.

Thus, we are left with the term independent of l:

m(γ

P



+ γ

Pγ

) = 4m[(1 − 2α)p

μ

+ (1 − 2β)p

]

→ 4m(1 − α − β)(p



+ p)

(13)

In the last step I used a handy trick; since D is symmetric under α ←→ β , we can sym-

metrize the terms we get in N

198 | III. Renormalization and Gauge Invariance

3. Finally, the most complicated m

term. The term quadratic in l: note that we can effectively

replace l

inside



l/(2π)

στ

by Lorentz invariance (this step is possible because

we have shifted the integration variable so that D is a Lorentz invariant function of l

.) Thus,

the term quadratic in l gives rise to a γ

term. Throw it away. Again we throw away the term

linear in l, leaving [use (D.6) here!]

P



Pγ

=−2 Pγ

P



→−2[(1 −β) p − αm]γ

[(1 − α) p



− βm] (14)

where in the last step we remembered that 

is to be sandwiched between ¯u(p



) and u(p).

Again, it is convenient to organize the terms in (14) by powers of m. With the various tricks

we have already used, we find that the m

term can be thrown away, the m term gives

2m(p



+ p)

[α(1 − α) + β(1 − β)], and the m

term gives 2m(p



+ p)

[−2(1 − α)(1 − β)].

Putting it altogether, we find that N

→ 2m(p



+ p)

(α + β)(1 − α − β)

We can now do the integral



l/(2π)

](1/D) using (D.11). Finally, we obtain



=−2ie



dα dβ(

−i

32π

)

(α + β)

=−

8π



+ p)

(15)

and thus, trumpets please:

(0) =

8π

2π

(16)

Schwinger’s announcement of this result in 1948 had an electrifying impact on the theo-

retical physics community.

I gave you in this chapter not one, but two, of the great triumphs of twentieth century

physics, although admittedly the first is not a result of field theory per se.

Exercises

III.6.1 Evaluate ¯u(p



)( p



+ γ

p)u(p) in two different ways and thus prove Gordon decomposition.

III.6.2 Check that (7) is consistent with current conservation. [Hint: By translation invariance (we suppress the

spin variable)

p



(x) |p=p



(0) |pe

i(p



−p)x

and hence

p



|∂

(x) |p=i(p



− p)

p



(0) |pe

i(p



−p)x

Thus current conservation implies that q

p



(0) |p=0.]

III.6.3 By Lorentz invariance the right hand side of (7) has to be a vector. The only possibilities are ¯uγ

(p + p



)

¯uu, and (p − p



)

¯uu. The last term is ruled out because it would not be consistent with current

conservation. Show that the form given in (7) is in fact the most general allowed.

III.6. Magnetic Moment of Electron | 199

III.6.4 In chapter II.6, when discussing electron-proton scattering, we ignored the strong interaction that the

proton participates in. Argue that the effects of the strong interaction could be included phenomenolog-

ically by replacing the vertex ¯u(P , S)γ

u(p, s) in (II.6.1) by

P , S|J

(0) |p, s=¯u(P , S)



) +

iσ

μν

)



u(p, s) (17)

Careful measurements of electron-proton scattering, thus determining the two proton form factors

) and F

), earned R. Hofstadter the 1961 Nobel Prize. While we could account for the general

behavior of these two form factors, we are still unable to calculate them from first principles (in contrast

to the corresponding form factors for the electron.) See chapters IV.2 and VII.3.

III.7

Polarizing the Vacuum and

Renormalizing the Charge

A photon can fluctuate into an electron and a positron

One early triumph of quantum electrodynamics is the understanding of how quantum

fluctuations affect the way the photon propagates. A photon can always metamorphose into

an electron and a positron that, after a short time mandated by the uncertainty principle,

annihilate each other becoming a photon again. The process, which keeps on repeating

itself, is depicted in figure III.7.1.

Quantum fluctuations are not limited to what we just described. The electron and

positron can interact by exchanging a photon, which in turn can change into an electron

and a positron, and so on and so forth. The full process is shown in figure III.7.2, where the

shaded object, denoted by i

μν

(q) and known as the vacuum polarization tensor, is given

by an infinite number of Feynman diagrams, as shown in figure III.7.3. Figure III.7.1 is

obtained from figure III.7.2 by approximating i

μν

(q) by its lowest order diagram.

It is convenient to rewrite the Lagrangian L =

ψ[iγ

(∂

− ieA

) − m]ψ −

μν

letting A → (1/e)A, which we are always allowed to do, so that

L =

ψ[iγ

(∂

− iA

) − m]ψ −

μν

(1)

Note that the gauge transformation leaving L invariant is given by ψ →e

iα

ψ and A

→

+∂

α. The photon propagator (chapter III.4), obtained roughly speaking by inverting

(1/4e

μν

, is now proportional to e

μν

(q) =

−ie



μν

− (1 − ξ)



(2)

Every time a photon is exchanged, the amplitude gets a factor of e

. This is just a trivial

but convenient change and does not affect the physics in the slightest. For example, in the

Feynman diagram we calculated in chapter II.6 for electron-electron scattering, the factor

can be thought of as being associated with the photon propagator rather than as coming

from the interaction vertices. In this interpretation e

measures the ease with which the

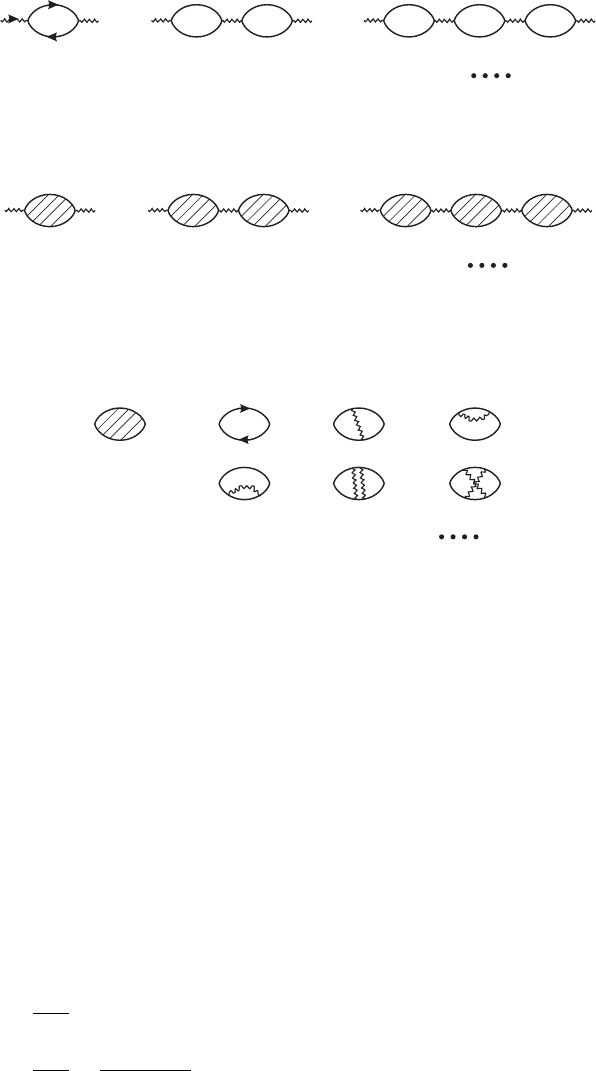
III.7. Polarizing the Vacuum | 201

Figure III.7.1

Figure III.7.2

p + q

Figure III.7.3

photon propagates through spacetime. The smaller e

, the more action it takes to have

the photon propagate, and the harder for the photon to propagate, the weaker the effect of

electromagnetism.

The diagrammatic proof of gauge invariance given in chapter II.7 implies that



μν

(q) = 0. Together with Lorentz invariance, this requires that



μν

(q) = (q

− g

μν

)(q

) (3)

The physical or renormalized photon propagator as shown in figure III.7.2 is then given

by the geometric series

μν

(q) = iD

μν

(q) + iD

μλ

(q)i

λρ

(q)iD

ρν

(q)

+ iD

μλ

(q)i

λρ

(q)iD

ρσ

(q)i

σκ

(q)iD

κν

(q) +

...

−ie

μν

{1 − e

(q

) + [e

(q

)]

...

}+q

term

−ie

μν

1 + e

(q

)

+ q

term (4)

Because of (3) the (1 − ξ)(q

) part of D

μλ

(q) is annihilated when it encounters



λρ

(q). Thus, in iD

μν

(q) the gauge parameter ξ enters only into the q

term and drops

out in physical amplitudes, as explained in chapter II.7.