Zee A. Quantum Field Theory in a Nutshell
Подождите немного. Документ загружается.


142 | II. Dirac and the Spinor
An often encountered case involves two particles scattering into two particles in the center of mass frame. Let
us do the phase space integral
(d
3
k
1
/2ω
1
)(d
3
k
2
/2ω
2
)δ
(4)
(P − k
1
− k
2
) here for easy reference. We will do it in
two different ways for your edification.
We could immediately integrate over d
3
k
2
thus knocking out the 3-dimensional momentum conservation
delta function δ
3
(
k
1
+
k
2
). Writing d
3
k
1
= k
2
1
dk
1
d, we integrate over the remaining energy conservation delta
function δ(
k
2
1
+ m
2
1
+
k
2
1
+ m
2
2
− E
total
). Using (I.2.13), we find that the integral over k
1
gives k
1
ω
1
ω
2
/E
total
,
where ω
1
≡
k
2
1
+ m
2
1
and ω
2
≡
k
2
1
+ m
2
2
, with k
1
determined by
k
2
1
+ m
2
1
+
k
2
1
+ m
2
2
=E
total
. Thus we obtain
d
3
k
1
2ω
1
d
3
k
2
2ω
2
δ
(4)
(P −k
1
− k
2
) =
k
1
4E
total
d (40)
Once again, if you use the “rest normalization" for fermions, remember to make the replacement as explained
above for the decay rate. The factor of
1
4
should be replaced by m
f
/2 for one fermion and one boson, and by
m
1
m
2
for two fermions.
Alternatively, we use (I.8.14) and regressing, write d
3
k
2
=
d
4
k
2
θ(k
0
2
)δ(k
2
2
−m
2
2
)2ω
2
. Integrate over d
4
k
2
and
knock out the 4-dimensional delta function, leaving us with
2ω
2
dk
1
k
2
1
d/(2ω
1
2ω
2
)δ((P − k
1
)
2
− m
2
2
). The
argument of the delta function is E
2
total
− 2E
total
k
1
+ m
2
1
− m
2
2
, and thus integrating over k
1
we get a factor of
2E
total
in the denominator, giving a result in agreement with (40).
For the record, you could work out the kinematics and obtain
k
1
=
(E
2
total
− (m
1
+ m
2
)
2
)(E
2
total
− (m
1
− m
2
)
2
)/2E
total
Evidently, this phase space integral also applies to the decay into two particles in the rest frame of the parent
particle, in which case we replace E
total
by M. In particular, for our toy example, we have
=
g
2
16πM
3
(M
2
− (m + μ)
2
)(M
2
− (m − μ)
2
) (41)
The differential cross section for two-into-two scattering in the center of mass frame is given by
dσ
d
=
1
(2π)
2
|v
1
−v
2
|2ω(p
1
)2ω(p
2
)
k
1
E
total
F |M|
2
(42)
In particular, in the text we calculated electron-electron scattering in the relativistic limit. As shown there, we
can write |M|
2
=|
M|
2
/(2m)
4
in terms of some reduced invariant amplitude
M. The factor 1/(2m)
4
transforms
the factors 2ω(p) into 2E. Things simplify enormously, with |v
1
−v
2
|=2 and k
1
=
1
2
E
total
, so that finally
dσ
d
=
1
2
4
(4π)
2
E
2
|
M|
2
(43)
Last, we come to the statistical factor S that must be included in calculating the total decay rate and the total
cross section to avoid over-counting if there are identical particles in the final state. The factor S has nothing to do
with quantum field theory per se and should already be familiar to you from nonrelativistic quantum mechanics.
The rule is that if there are n
i
identical particles of type i in the final state, the total decay rate or the total cross
section must be multiplied by S =
i
1/n
i
! to account for indistinguishability.
To see the necessity for this factor, it suffices to think about the simplest case of two identical Bose particles.
To be specific, consider electron-positron annihilation into two photons (which we will study in chapter II.8). For
simplicity, average and sum over all spin polarizations. Let us calculate dσ /d according to (43) above. This is
the probability that a photon will check into a detector set up at angles θ and φ relative to the beam direction. If
the detector clicks, then we know that the other photon emerged at an angle π −θ relative to the beam direction.
Thus the total cross section should be
σ =
1
2
d
dσ
d
=
1
2
π
0
dθ
dσ
dθ
(44)
(The second equality is for all the elementary cases we will encounter in which dσ does not depend on the
azimuthal angle φ.) In other words, to avoid double counting, we should divide by 2 if we integrate over the full
angular range of θ.
More formally, we argue as follows. In quantum mechanics, a set of states |α is complete if 1 =
α
|αα|
(“decomposition of 1”). Acting with this on |β we see that these states must be normalized according to
α|β=δ
αβ
.
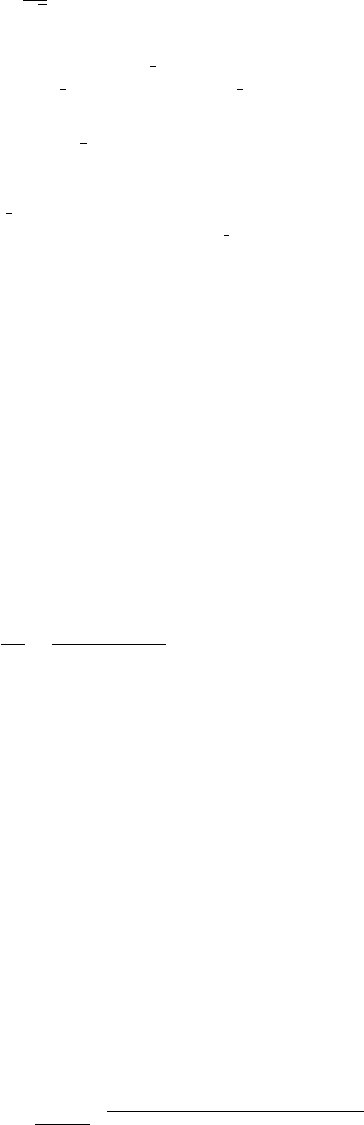
II.6. Scattering and Gauge Invariance | 143
Now consider the state
|k
1
, k
2
≡
1
√
2
˜a
†
(k
1
) ˜a
†
(k
2
) |0=|k
2
, k
1
(45)
containing two identical bosons. By repeatedly using the commutation relation (32), we compute q
1
, q
2
|k
1
, k
2
=
0|˜a(q
1
) ˜a(q
2
) ˜a
†
(k
1
) ˜a
†
(k
2
) |0=
1
2
(δ
q
1
k
1
δ
q
2
k
2
+ δ
q
2
k
1
δ
q
1
k
2
). Thus
q
1
q
2
|q
1
, q
2
q
1
, q
2
|k
1
, k
2
=
q
1
q
2
|q
1
, q
2
1
2
(δ
q
1
k
1
δ
q
2
k
2
+ δ
q
2
k
1
δ
q
1
k
2
) =
1
2
( |k
1
, k
2
+|k
2
, k
1
) =|k
1
, k
2
. Thus the states |k
1
, k
2
are nor-
malized properly. In the sum over states, we have 1 =
...
+
q
1
q
2
|q
1
, q
2
q
1
, q
2
|+
...
.
In other words, if we are to sum over q
1
and q
2
independently, then we must normalize our states as in (45)
with the factor of 1/
√
2. But then this factor would appear multiplying M. In calculating the total decay rate
or the total cross section, we are effectively summing over a complete set of final states. In summary, we have
two options: either we treat the integration over d
3
k
1
d
3
k
2
as independent in which case we have to multiply the
integral by
1
2
, or we integrate over only half of phase space.
We readily generalize from this factor of
1
2
to the statistical factor S.
In closing, let me mention two interesting pieces of physics.
To calculate the cross section σ , we have to divide by the flux, and hence σ is proportional to 1/|v
1
−v
2
|.
For exothermal processes, such as electron-positron annihilation into photons or slow neutron capture, σ could
become huge as the relative velocity v
rel
→ 0. Fermi exploited this fact to great advantage in studying nuclear
fission. Note that although the cross section, which has dimension of an area, formally goes to infinity, the
reaction rate (the number of reactions per unit time) remains finite.
Positronium decay into photons is an example of a bound state decaying in finite time. In positronium, the
positron and electron are not approaching each other in plane wave states, as we assumed in our cross section
calculation. Rather, the probability (per unit volume) that the positron finds itself near the electron is given by
|ψ(0)|
2
according to elementary quantum mechanics, with ψ(x) the bound state wave function for whatever
state of positronium we are interested in. In other words, |ψ(0)|
2
gives the volume density of positrons near the
electron. Since vσ is a volume divided by time, the decay rate is given by = vσ |ψ(0)|
2
.
Exercises
II.6.1 Show that the differential cross section for a relativistic electron scattering in a Coulomb potential is
given by
dσ
d
=
α
2
4 p
2
v
2
sin
4
(θ/2)
(1 − v
2
sin
2
(θ/2)).
Known as the Mott cross section, it reduces to the Rutherford cross section you derived in a course on
quantum mechanics in the limit the electron velocity v → 0.
II.6.2 To order e
2
the amplitude for positron scattering off a proton is just minus the amplitude (3) for electron
scattering off a proton. Thus, somewhat counterintuitively, the differential cross sections for positron
scattering off a proton and for electron scattering off a proton are the same to this order. Show that to
the next order this is no longer true.
II.6.3 Show that the trace of a product of odd number of gamma matrices vanishes.
II.6.4 Prove the identity s +t +u =
a
m
2
a
.
II.6.5 Verify the differential cross section for relativistic electron electron scattering given in (25).
II.6.6 For those who relish long calculations, determine the differential cross section for electron-electron
scattering without taking the relativistic limit.
II.6.7 Show that the decay rate for one boson of mass M into two bosons of masses m and μ is given by
=
|M|
2
16πM
3
(M
2
− (m + μ)
2
)(M
2
− (m − μ)
2
)

II.7 Diagrammatic Proof of Gauge Invariance
Gauge invariance
Conceptually, rather than calculate cross sections, we have the more important task of
proving that we can indeed set the photon mass μ equal to zero with impunity in calculating
any physical process. With μ = 0, the Lagrangian given in chapter II.1 becomes the
Lagrangian for quantum electrodynamics:
L =
¯
ψ[iγ
μ
(∂
μ
− ieA
μ
) − m]ψ −
1
4
F
μν
F
μν
(1)
We are now ready for one of the most important observations in the history of theoretical
physics. Behold, the Lagrangian is left invariant by the gauge transformation
ψ(x) →e
i(x)
ψ(x) (2)
and
A
μ
(x) → A
μ
(x) +
1
ie
e
−i(x)
∂
μ
e
i(x)
= A
μ
(x) +
1
e
∂
μ
(x) (3)
which implies
F
μν
(x) → F
μν
(x) (4)
You are of course already familiar with (3) and the invariance of F
μν
from classical
electromagnetism.
In contemporary theoretical physics, gauge invariance
1
is regarded as fundamental and
all important, as we will see later. The modern philosophy is to look at (1) as a consequence
of (2) and (3). If we want to construct a gauge invariant relativistic field theory involving a
spin
1
2
and a spin 1 field, then we are forced to quantum electrodynamics.
1
The discovery of gauge invariance was one of the most arduous in the history of physics. Read J. D. Jackson
and L. B. Okun, “Historical roots of gauge invariance,” Rev. Mod. Phys. 73, 2001 and learn about the sad story of
a great physicist whose misfortune in life was that his name differed from that of another physicist by only one
letter.
II.7. Proof of Gauge Invariance | 145
You will notice that in (3) I have carefully given two equivalent forms. While it is simpler,
and commonly done in most textbooks, to write the second form, we should also keep the
first form in mind. Note that (x) and (x) + 2π give exactly the same transformation.
Mathematically speaking, the quantities e
i(x)
and ∂
μ
(x) are well defined, but (x) is
not.
After these apparently formal but actually physically important remarks, we are ready
to work on the proof. I will let you give the general proof, but I will show you the way by
working through some representative examples.
Recall that the propagator for the hypothetical massive photon is iD
μν
= i(k
μ
k
ν
/μ
2
−
g
μν
)/(k
2
− μ
2
). We can set the μ
2
in the denominator equal to zero without further ado
and write the photon propagator effectively as iD
μν
=i(k
μ
k
ν
/μ
2
−g
μν
)/k
2
. The dangerous
term is k
μ
k
ν
/μ
2
. We want to show that it goes away.
A specific example
First consider electron-electron scattering to order e
4
. Of the many diagrams, focus on the
two in figure II.7.1.a. The Feynman amplitude is then
¯u(p
)
γ
λ
1
p+ k − m
γ
μ
+ γ
μ
1
p
− k − m
γ
λ
u(p)
i
k
2
k
μ
k
ν
μ
2
− δ
ν
μ
λν
(5)
where
λν
is some factor whose detailed structure does not concern us. For the specific
case shown in figure II.7.1a we can of course write out
λν
explicitly if we want. Note the
plus sign here from interchanging the two photons since photons obey Bose statistics.
p + k
λ
μ
p’ − k
λ
μ
(a)
p’
k
p
p’
k
p
k’
k’
Figure II.7.1
146 | II. Dirac and the Spinor
(b)
p’
k
p
p’
k
p
p’ − k
λ
μ
p + k
λ
μ
Figure II.7.1 (continued)
Focus on the dangerous term. Contracting the ¯u(p
)(
...
)u(p) factor in (5) with k
μ
we
have
¯u(p
)
γ
λ
1
p+ k − m
k+ k
1
p
− k − m
γ
λ
u(p) (6)
The trick is to write the k in the numerator of the first term as (p+ k − m) −(p −m), and
in the numerator of the second term as (p
−m) − (p
− k −m). Using (p − m)u(p) = 0
and ¯u(p
)(p
−m) = 0, we see that the expression in (6) vanishes. This proves the theorem
in this simple example. But since the explicit form of
λν
did not enter, the proof would
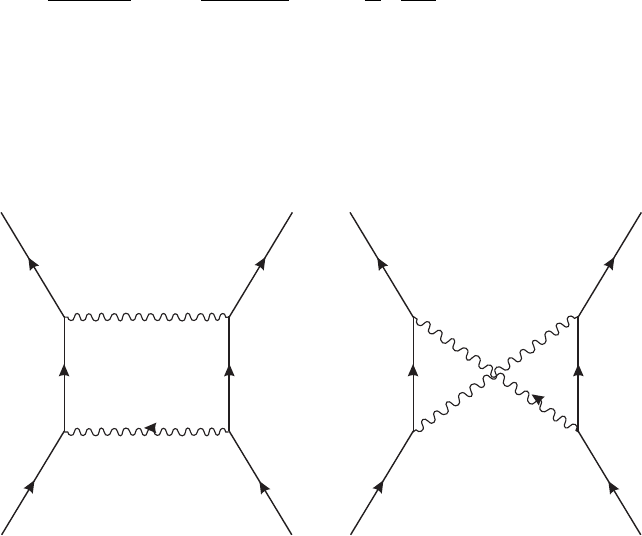
have gone through even if figure II.7.1a were replaced by the more general figure II.7.1b,
where arbitrarily complicated processes could be going on under the shaded blob.
Indeed we can generalize to figure II.7.1c. Apart from the photon carrying momentum
k that we are focusing on, there are already n photons attached to the electron line. These
n photons are just “spectators” in the proof in the same way that the photon carrying
momentum k
in figure II.7.1a never came into the proof that (6) vanishes. The photon
we are focusing on can attach to the electron line in n + 1 different places. You can now
extend the proof as an exercise.
Photon landing on an internal line
In the example we just considered, the photon line in question lands on an external electron
line. The fact that the line is “capped at the two ends” by ¯u(p
) and u(p) is crucial in the
proof. What if the photon line in question lands on an internal line?
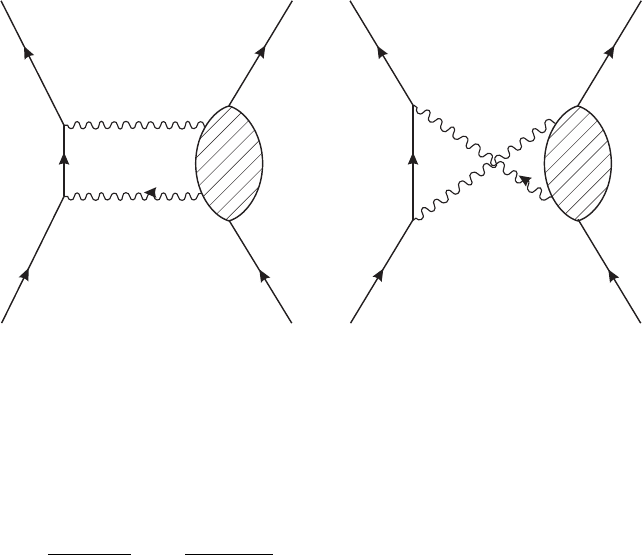
An example is shown in figure II.7.2, contributing to electron-electron scattering in
order e
8
. The figure contains three distinct diagrams. The electron “on the left” emits

II.7. Proof of Gauge Invariance | 147
(c)
p’
k
p
Figure II.7.1 (continued)
three photons, which attach to an internal electron loop. The electron “on the right”
emits a photon with momentum k, which can attach to the loop in three distinct ways.
Since what we care about is whether the k
μ
k
ρ
/μ
2
piece in the photon propagator
i(k
μ
k
ρ
/μ
2
− g
μρ
)/k
2
goes away or not, we can for our purposes replace that photon
propagator by k
μ
. To save writing slightly, we define p
1
=p + q
1
and p
2
=p
1
+q
2
(see the
momentum labels in figure II.7.2): Let’s focus on the relevant part of the three diagrams,
referring to them as A, B, and C.
A =
d
4
p
(2π)
4
tr
γ
ν
1
p
2
+ k − m
γ
σ
1
p
1
+ k − m
γ
λ
1
p+ k − m
k
1
p − m
(7)
B =
d
4
p
(2π)
4
tr
γ
ν
1
p
2
+ k − m
γ
σ
1
p
1
+ k − m
k
1
p
1
− m
γ
λ
1
p − m
(8)
and
C =
d
4
p
(2π)
4
tr
γ
ν
1
p
2
+ k − m
k
1
p
2
− m
γ
σ
1
p
1
− m
γ
λ
1
p − m
(9)
This looks like an unholy mess, but it really isn’t. We use the same trick we used before.
In C write k = ( p
2
+ k − m) − (p
2
− m), so that
C =
d
4
p
(2π)
4
tr
γ
ν
1
p
2
− m
γ
σ
1
p
1
− m
γ
λ
1
p − m
− tr
γ
ν
1
p
2
+ k − m
γ
σ
1
p
1
− m
γ
λ
1
p − m
(10)
In B write k = ( p
1
+ k − m) − ( p
1
− m), so that
B =
d
4
p
(2π)
4
tr(γ
ν
1
p
2
+ k − m
γ
σ
1
p
1
− m
γ
λ
1
p − m
)
− tr
γ
ν
1
p
2
+ k − m
γ
σ
1
p
1
+ k − m
γ
λ
1
p − m
(11)
148 | II. Dirac and the Spinor
p + k
k
p
p
1
+ k
p
2
+ k
q
1
q
2
−(q
1
+ q
2
+ k)
λ
σ
ν
A
k
p
p
1
+ k
p
2
+ k
q
1
q
2
−(q
1
+ q
2
+ k)
λ
σ
ν
B
p
1
k
p
p
2
p
2
+k
q
1
q
2
−(q
1
+ q
2
+ k)
λ
σ
ν
C
p
1
Figure II.7.2

II.7. Proof of Gauge Invariance | 149
Finally, in A write k = ( p+ k − m) − ( p − m)
A =
d
4
p
(2π)
4
tr
γ
ν
1
p
2
+ k − m
γ
σ
1
p
1
+ k − m
γ
λ
1
p − m
− tr
γ
ν
1
p
2
+ k − m
γ
σ
1
p
1
+ k − m
γ
λ
1
p+ k − m
(12)
Now you see what is happening. When we add the three diagrams together terms cancel
in pairs, leaving us with
A + B + C =
d
4
p
(2π)
4
tr
γ
ν
1
p
2
− m
γ
σ
1
p
1
− m
γ
λ
1
p − m
− tr
γ
ν
1
p
2
+ k − m
γ
σ
1
p
1
+ k − m
γ
λ
1
p+ k − m
(13)
If we shift (see exercise II.7.2) the dummy integration variable p → p − k in the second
term, we see that the two terms cancel. Indeed, the k
μ
k
ρ
/μ
2
piece in the photon propagator
goes away and we can set μ = 0.
I will leave the general proof to you. We have done it for one particular process. Try it
for some other process. You will see how it goes.
Ward-Takahashi identity
Let’s summarize. Given any physical amplitude T
μ
...
(k,
...
) with external electrons on
shell [this is jargon for saying that all necessary factors u(p) and ¯u(p) are included in
T
μ
...
(k,
...
)] describing a process with a photon carrying momentum k coming out of, or
going into, a vertex labeled by the Lorentz index μ, we have
k
μ
T
μ
...
(k,
...
) = 0 (14)
This is sometimes known as a Ward-Takahashi identity.
The bottom line is that we can write iD
μν
=−ig
μν
/k
2
for the photon propagator. Since
we can discard the k
μ
k
ν
/μ
2
term in the photon propagator i(k
μ
k
ν
/μ
2
− g
μν
)/k
2
we can
also add in a k
μ
k
ν
/k
2
term with an arbitrary coefficient. Thus, for the photon propagator
we can use
iD
μν
=
i
k
2
(
1 − ξ
)
k
μ
k
ν
k
2
− g
μν
(15)
where we can choose the number ξ to simplify our calculation as much as possible.
Evidently, the choice of ξ amounts to a choice of gauge for the electromagnetic field. In
particular, the choice ξ =1 is known as the Feynman gauge, and the choice ξ =0 is known
as the Landau gauge. If you find an especially nice choice, you can have a gauge named
after you as well! For fairly simple calculations, it is often advisable to calculate with an
arbitrary ξ . The fact that the end result must not depend on ξ provides a useful check on
the arithmetic.

150 | II. Dirac and the Spinor
This completes the derivation of the Feynman rules for quantum electrodynamics: They
are the same rules as those given in chapter II.5 for the massive vector boson theory except
for the photon propagator given in (15).
We have given here a diagrammatic proof of the gauge invariance of quantum
electrodynamics. We will worry later (in chapter IV.7) about the possibility that the shift of
integration momentum used in the proof may not be allowed in some cases.
The longitudinal mode
We now come back to the worry we had in chapter I.5. Consider a massive spin 1 meson
moving along the z−direction. The 3 polarization vectors are fixed by the condition k
λ
ε
λ
=
0 with k
λ
=(ω,0,0,k) (recall chapter I.5) and the normalization ε
λ
ε
λ
=−1, so that ε
(1)
λ
=
(0, 1, 0, 0), ε
(2)
λ
=(0, 0, 1, 0), ε
(3)
λ
=(−k,0,0,ω)/μ. Note that as μ → 0, the longitudinal
polarization vector ε
(3)
λ
becomes proportional to k
λ
= (ω,0,0,−k). The amplitude for
emitting a meson with a longitudinal polarization in the process described by (14) is
given by ε
(3)
λ
T
λ
...
= (−kT
0
...
+ ωT
3
...
)/μ = (−kT
0
...
+
k
2
+ μ
2
T
3
...
)/μ (−kT
0
...
+
(k +
μ
2
2k
)T
3
...
)/μ (for μ k), namely −(k
λ
T
λ
...
/μ) +
μ
2k
T
3
...
with k
λ
=(k,0,0,−k). Upon
using (14) we see that the amplitude ε
(3)
λ
T
λ
...
→
μ
2k
T
3
...
→ 0asμ → 0.
The longitudinal mode of the photon does not exist because it decouples from all physical
processes.
Here is an apparent paradox. Mr. Boltzmann tells us that in thermal equilibrium each
degree of freedom is associated with
1
2
T . Thus, by measuring some thermal property (such
as the specific heat) of a box of photon gas to an accuracy of 2/3 an experimentalist could
tell if the photon is truly massless rather than have a mass of a zillionth of an electron volt.
The resolution is of course that as the coupling of the longitudinal mode vanishes as
μ → 0 the time it takes for the longitudinal mode to come to thermal equilibrium goes to
infinity. Our crafty experimentalist would have to be very patient.
Emission and absorption of photons
According to chapter II.5, the amplitude for emitting or absorbing an external on-shell
photon with momentum k and polarization a(a= 1, 2) is given by ε
(a)
μ
(k)T
μ
...
(k,
...
).
Thanks to (14), we are free to vary the polarization vector
ε
(a)
μ
(k) → ε
(a)
μ
(k) + λk
μ
(16)
for arbitrary λ. You should recognize (16) as the momentum space version of (3). As we
will see in the next chapter, by a judicious choice of ε
(a)
μ
(k), we can simplify a given
calculation considerably. In one choice, known as the “transverse gauge,” the 4-vectors
ε
(a)
μ
(k) = (0, ε(k)) for a = 1, 2 do not have time components. (For a photon moving in the
z-direction, this is just the choice specified in the preceding section.)

II.7. Proof of Gauge Invariance | 151
Exercises
II.7.1 Extend the proof to cover figure II.7.1c. [Hint: To get oriented, note that figure II.7.1b corresponds to
n = 1.]
II.7.2 You might have worried whether the shift of integration variable is allowed. Rationalizing the denomi-
nators in the first integral
d
4
p
(2π)
4
tr(γ
ν
1
p
2
− m
γ
σ
1
p
1
− m
γ
λ
1
p − m
)
in (13) and imagining doing the trace, you can convince yourself that this integral is only logarithmically
divergent and hence that the shift is allowed. This issue will come up again in chapter IV.7 and we are
anticipating a bit here.
