Zee A. Quantum Field Theory in a Nutshell
Подождите немного. Документ загружается.

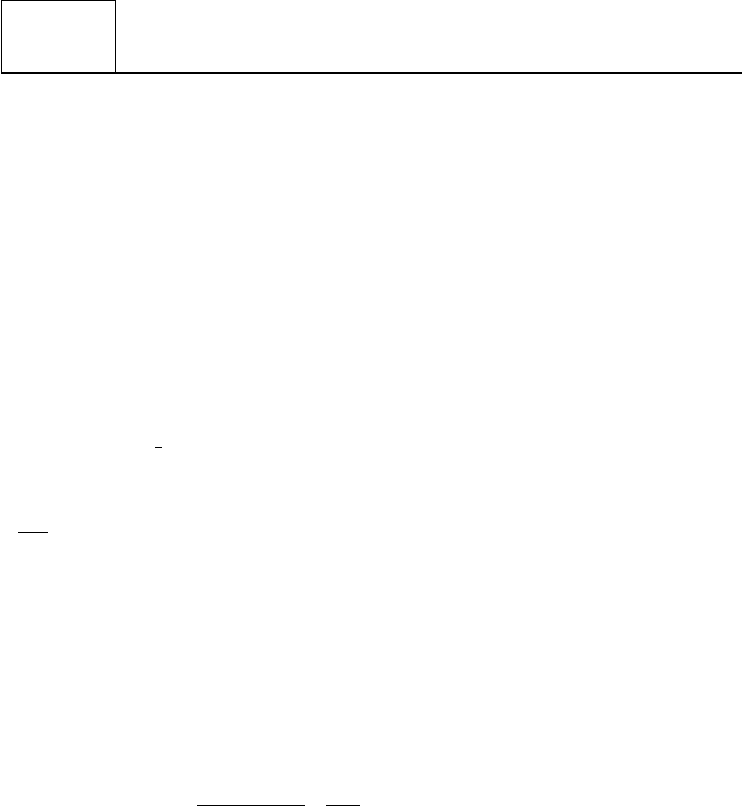
II.6 Electron Scattering and Gauge Invariance
Electron-proton scattering
We will now finally calculate a physical process that experimentalists can go out and
measure. Consider scattering an electron off a proton. (For the moment let us ignore the
strong interaction that the proton also participates in. We will learn in chapter III.6 how
to take this fact into account. Here we pretend that the proton, just like the electron, is a
structureless spin-
1
2
fermion obeying the Dirac equation.) To order e
2
the relevant Feynman
diagram is given in figure II.6.1 in which the electron and the proton exchange a photon.
But wait, from chapter I.5 we only know how to write down the propagator iD
μν
=
i
k
μ
k
ν
μ
2
−η
μν
/(k
2
−μ
2
) for a hypothetical massive photon. (Trivial notational change: the
mass of the photon is now called μ, since m is reserved for the mass of the electron and
M for the mass of the proton.) In that chapter I outlined our philosophy: we will plunge
ahead and calculate with a nonzero μ and hope that at the end we can set μ to zero. Indeed,
when we calculated the potential energy between two external charges, we find that we can
let μ → 0 without any signs of trouble [see (I.5.6)]. In this chapter and the next, we would
like to see whether this will always be the case.
Applying the Feynman rules, we obtain the amplitude for the diagram in figure II.6.1
(with k = P − p the momentum transfer in the scattering)
M(P , P
N
) = (−ie)(ie)
i
(P −p)
2
− μ
2
k
μ
k
ν
μ
2
− η
μν
¯u(P )γ
μ
u(p) ¯u(P
N
)γ
ν
u(p
N
) (1)
We have suppressed the spin labels and used the subscript N (for nucleon) to refer to the
proton.
Now notice that
k
μ
¯u(P )γ
μ
u(p) = (P −p)
μ
¯u(P )γ
μ
u(p) =¯u(P )(P − p)u(p) =¯u(P )(m − m)u(p) = 0 (2)
by virtue of the equations of motion satisfied by ¯u(P ) and u(p). Similarly, k
μ
¯u(P
N
)γ
μ
u(p
N
)
= 0.

II.6. Scattering and Gauge Invariance | 133
k
P
N
p
N
P
p
Figure II.6.1
This important observation implies that the k
μ
k
ν
/μ
2
term in the photon propagator does
not enter. Thus
M(P , P
N
) =−ie
2
1
(P −p)
2
− μ
2
¯u(P )γ
μ
u(p) ¯u(P
N
)γ
μ
u(p
N
) (3)
and we can now set the photon mass μ to zero with impunity and replace (P − p)
2
− μ
2
in the denominator by (P − p)
2
.
Note that the identity that allows us to set μ to zero is just the momentum space version
of electromagnetic current conservation ∂
μ
J
μ
= ∂
μ
(
¯
ψγ
μ
ψ) = 0. You would notice that
this calculation is intimately related to the one we did in going from (I.5.4) to (I.5.5), with
¯u(P )γ
μ
u(p) playing the role of J
μ
(k).
Potential scattering
That the proton mass M is so much larger than the electron mass m allows us to make
a useful approximation familiar from elementary physics. In the limit M/m tending to
infinity, the proton hardly moves, and we could use, for the proton, the spinors for a particle
at rest given in chapter II.2, so that ¯u(P
N
)γ
0
u(p
N
) ≈ 1 and ¯u(P
N
)γ
i
u(p
N
) ≈ 0. Thus
M =
−ie
2
k
2
¯u(P )γ
0
u(p) (4)
We recognize that we are scattering the electron in the Coulomb potential generated by
the proton. Work out the (familiar) kinematics: p = (E ,0,0,|p|) and P = (E,0,|p|sin θ ,
|p| cos θ). We see that k = P − p is purely spacelike and k
2
=−
k
2
=−4|p|
2
sin
2
(θ/2).
Recall from (I.4.7) that
d
3
xe
i
k
.
x
−
e
4πr
=−
e
k
2
(5)
We represent potential scattering by the Feynman diagram in figure II.6.2: the proton has
disappeared and been replaced by a cross, which supplies the virtual photon the electron
interacts with. It is in this sense that you could think of the Coulomb potential picturesquely
as a swarm of virtual photons.
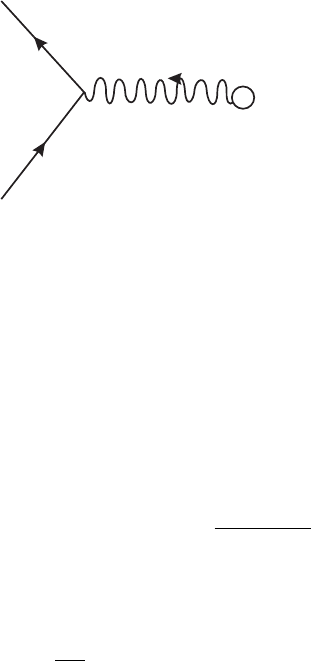
134 | II. Dirac and the Spinor
k
X
P
p
Figure II.6.2
Once again, it is instructive to use the canonical formalism to derive this expression for
M for potential scattering. We want the transition amplitude P , S|e
−iHT
|p, s with the
single electron state |p, s≡b
†
(p, s)|0. The term in the Lagrangian describing the elec-
tron interacting with the external c-number potential A
μ
(x) is given in (II.5.22) and thus
to leading order we have the transition amplitude ie
d
4
xP , S|
¯
ψ(x)γ
μ
ψ(x)|p, sA
μ
(x).
Using (II.2.10–11) we evaluate this as
ie
d
4
x(1/ρ(P ))(1/ρ(p))( ¯u(P , S)γ
μ
u(p, s))e
i(P−p)x
A
μ
(x)
Here ρ(p) denotes the fermion normalization factor
(2π)
3
E
p
/m in (II.2.10). Given that
the Coulomb potential has only a time component and does not depend on time, we see
that integration over time gives us an energy conservation delta function, and integration
over space the Fourier transform of the potential, as in (5). Thus the above becomes
(1/ρ(P ))(1/ρ(p))(2π)δ(E
P
−E
p
)(
−ie
2
k
2
) ¯u(P , S)γ
0
u(p, s). Satisfyingly, we have recovered
the Feynman amplitude up to normalization factors and an energy conservation delta
function, just as in (I.8.16) except for the substitution of boson for fermion normalization
factors. Notice that we have energy conservation but not 3-momentum conservation, a fact
we understand perfectly well when we dribble a basketball ball, for example.
Electron-electron scattering
Next, we graduate to two electrons scattering off each other: e
−
(p
1
) + e
−
(p
2
) → e
−
(P
1
) +
e
−
(P
2
). Here we have a new piece of physics: the two electrons are identical. A profound
tenet of quantum physics states that we cannot distinguish between the two outgoing
electrons. Now there are two Feynman diagrams (see fig. II.6.3) to order e
2
, obtained
by interchanging the two outgoing electrons. The electron carrying momentum P
1
could
have “come from” the incoming electron carrying momentum p
1
or the incoming electron
carrying momentum p
2
.
We have for figure II.6.3a the amplitude
A(P
1
, P
2
) = (ie
2
/(P
1
− p
1
)
2
) ¯u(P
1
)γ
μ
u(p
1
) ¯u(P
2
)γ
μ
u(p
2
)
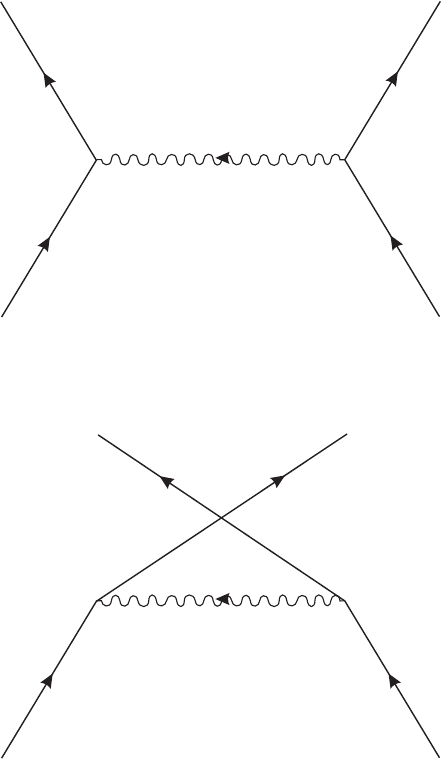
II.6. Scattering and Gauge Invariance | 135
(a)
P
1
P
2
p
1
p
2
k
(b)
P
1
P
2
p
1
p
2
Figure II.6.3
as before. We have only indicated the dependence of A on the final momenta, suppressing
the other dependence. By Fermi statistics, the amplitude for the diagram in figure II.6.3
is then −A(P
2
, P
1
). Thus the invariant amplitude for two electrons of momentum p
1
and
p
2
to scatter into two electrons with momentum P
1
and P
2
is
M = A(P
1
, P
2
) − A(P
2
, P
1
) (6)
To obtain the cross section we have to square the amplitude
|M|
2
= [|A(P
1
, P
2
)|
2
+ (P
1
↔ P
2
)] −2ReA(P
2
, P
1
)
∗
A(P
1
, P
2
) (7)

136 | II. Dirac and the Spinor
At this point we have to do a fair amount of arithmetic, but keep in mind that there
is nothing conceptually intricate in what follows. First, we have to learn to complex con-
jugate spinor amplitudes. Using (II.1.15), note that in general ( ¯u(p
)γ
μ
...
γ
ν
u(p))
∗
=
u(p)
†
γ
†
ν
...
γ
†
μ
γ
0
u(p
) =¯u(p)γ
ν
...
γ
μ
u(p
). Here γ
μ
...
γ
ν
represents a product of any
number of γ matrices. Complex conjugation reverses the order of the product and inter-
changes the two spinors. Thus we have
|A(P
1
, P
2
)|
2
=
e
4
k
4
[ ¯u(P
1
)γ
μ
u(p
1
) ¯u(p
1
)γ
ν
u(P
1
)][ ¯u(P
2
)γ
μ
u(p
2
) ¯u(p
2
)γ
ν
u(P
2
)] (8)
which factorizes with one factor involving spinors carrying momentum with subscript 1
and another factor involving spinors carrying momentum with subscript 2. In contrast,
the interference term A(P
2
, P
1
)
∗
A(P
1
, P
2
) does not factorize.
In the simplest experiments, the initial electrons are unpolarized, and the polarization
of the outgoing electrons is not measured. We average over initial spins and sum over final
spins using (II.2.8):
s
u(p, s)¯u(p, s) =
p + m
2m
(9)
In averaging and summing |A(P
1
, P
2
)|
2
we encounter the object (displaying the spin labels
explicitly)
τ
μν
(P
1
, p
1
) ≡
1
2
¯u(P
1
, S)γ
μ
u(p
1
, s)¯u(p
1
, s)γ
ν
u(P
1
, S) (10)
=
1
2(2m)
2
tr(P
1
+ m)γ
μ
(p
1
+ m)γ
ν
(11)
which is to be multiplied by τ
μν
(P
2
, p
2
).
Well, we, or rather you, have to develop some technology for evaluating the trace of
products of gamma matrices. The key observation is that the square of a gamma matrix
is either +1or−1, and different gamma matrices anticommute. Clearly, the trace of a
product of an odd number of gamma matrices vanish. Furthermore, since there are only
four different gamma matrices, the trace of a product of six gamma matrices can always be
reduced to the trace of a product of four gamma matrices, since there are always pairs of
gamma matrices that are equal and can be brought together by anticommuting. Similarly
for the trace of a product of an even higher number of gamma matrices.
Hence τ
μν
(P
1
, p
1
) =
1
2(2m)
2
(tr(P
1
γ
μ
p
1
γ
ν
) + m
2
tr(γ
μ
γ
ν
)). Writing tr(P
1
γ
μ
p
1
γ
ν
) =
P
1ρ
p
1λ
tr(γ
ρ
γ
μ
γ
λ
γ
ν
) and using the expressions for the trace of a product of an even
number of gamma matrices listed in appendix D, we obtain τ
μν
(P
1
, p
1
) =
1
2(2m)
2
4(P
μ
1
p
ν
1
−
η
μν
P
1
.
p
1
+ P
ν
1
p
μ
1
+ m
2
η
μν
).
In averaging and summing A(P
2
, P
1
)
∗
A(P
1
, P
2
) we encounter the more involved object
κ ≡
1
2
2
¯u(P
1
)γ
μ
u(p
1
) ¯u(P
2
)γ
μ
u(p
2
) ¯u(p
1
)γ
ν
u(P
2
) ¯u(p
2
)γ
ν
u(P
1
) (12)
where for simplicity of notation we have suppressed the spin labels. Applying (9) we can
write κ as a single trace. The evaluation of κ is quite tedious, since it involves traces of
products of up to eight gamma matrices.

II.6. Scattering and Gauge Invariance | 137
We will be content to study electron-electron scattering in the relativistic limit in which
m may be neglected compared to the momenta. As explained in chapter II.2, while we
are using the “rest normalization” for spinors we can nevertheless set m to 0 wherever
possible. Then
κ =
1
4(2m)
4
tr(P
1
γ
μ
p
1
γ
ν
P
2
γ
μ
p
2
γ
ν
) (13)
Applying the identities in appendix D to (13) we obtain tr(P
1
γ
μ
p
1
γ
ν
P
2
γ
μ
p
2
γ
ν
) =
−2tr(P
1
γ
μ
p
1
p
2
γ
μ
P
2
) =−32p
1
.
p
2
P
1
.
P
2
.
In the same limit τ
μν
(P
1
, p
1
) =
2
(2m)
2
(P
μ
1
p
ν
1
+ P
ν
1
p
μ
1
− η
μν
P
1
.
p
1
) and thus
τ
μν
(P
1
, p
1
)τ
μν
(P
2
, p
2
) =
4
(2m)
4
(P
μ
1
p
ν
1
+ P
ν
1
p
μ
1
− η
μν
P
1
.
p
1
)(2P
2μ
p
2ν
− η
μν
P
2
.
p
2
) (14)
=
4
.
2
(2m)
4
(p
1
.
p
2
P
1
.
P
2
+ p
1
.
P
2
p
2
.
P
1
) (15)
An amusing story to break up this tedious calculation: Murph Goldberger, who was
a graduate student at the University of Chicago after working on the Manhattan Project
during the war and whom I mentioned in chapter II.1 regarding the Feynman slash, told
me that Enrico Fermi marvelled at this method of taking a trace that young people were
using to sum over spin-
1
2
polarizations. Fermi and others in the older generation had
simply memorized the specific form of the spinors in the Dirac basis (which you know from
doing exercise II.1.3) and consequently the expressions for ¯u(P , S)γ
μ
u(p, s). They simply
multiplied these expressions together and added up the different possibilities. Fermi was
skeptical of the fancy schmancy method the young Turks were using and challenged Murph
to a race on the blackboard. Of course, with his lightning speed, Fermi won. To me, it is
amazing, living in the age of string theory, that another generation once regarded the
trace as fancy math. I confessed that I was even a bit doubtful of this story until I looked at
Feynman’s book Quantum Electrodynamics, but guess what, Feynman indeed constructed,
on page 100 in the edition I own, a table showing the result for the amplitude squared for
various spin polarizations. Some pages later, he mentioned that polarizations could also
be summed using the spur (the original German word for trace). Another amusing aside:
spur is cognate with the English word spoor, meaning animal droppings, and hence also
meaning track, trail, and trace. All right, back to work!
While it is not the purpose of this book to teach you to calculate cross sections for a
living, it is character building to occasionally push calculations to the bitter end. Here
is a good place to introduce some useful relativistic kinematics. In calculating the cross
section for the scattering process p
1
+p
2
→P
1
+P
2
(with the masses of the four particles
all different in general) we typically encounter Lorentz invariants such as p
1
.
P
2
. A priori,
you might think there are six such invariants, but in fact, you know that there are only
physical variables, the incident energy E and the scattering angle θ. The cleanest way to
organize these invariants is to introduce what are called Mandelstam variables:
s ≡ (p
1
+ p
2
)
2
= (P
1
+ P
2
)
2
(16)
t ≡(P
1
− p
1
)
2
= (P
2
− p
2
)
2
(17)
u ≡ (P
2
− p
1
)
2
= (P
1
− p
2
)
2
(18)
138 | II. Dirac and the Spinor
You know that there must be an identity reducing the three variables s, t, and u to two.
Show that (with an obvious notation)
s + t +u = m
2
1
+ m
2
2
+ M
2
1
+ M
2
2
(19)
For our calculation here, we specialize to the center of mass frame in the relativistic limit
p
1
=E(1, 0, 0, 1), p
2
=E(1, 0, 0, −1), P
1
=E(1, sin θ ,0,cosθ), and P
2
=E(1, −sin θ ,0,
− cos θ). Hence
p
1
.
p
2
= P
1
.
P
2
= 2E
2
=
1
2
s (20)
p
1
.
P
1
= p
2
.
P
2
= 2E
2
sin
2
θ
2
=−
1
2
t (21)
and
p
1
.
P
2
= p
2
.
P
1
= 2E
2
cos
2
θ
2
=−
1
2
u (22)
Also, in this limit (P
1
−p
1
)
4
=(−2p
1
.
P
1
)
2
=16E
4
sin
4
(θ/2) = t
4
. Putting it together, we
obtain
1
4
|M|
2
= (e
4
/4m
4
)f (θ), where
f(θ)=
s
2
+ u
2
t
2
+
2s
2
tu
+
s
2
+ t
2
u
2
=
s
4
+ t
4
+ u
4
t
2
u
2
=
1 + cos
4
(θ/2)
sin
4
(θ/2)
+
2
sin
2
(θ/2) cos
2
(θ/2)
+
1 + sin
4
(θ/2)
cos
4
(θ/2)
(23)
= 2
1
sin
4
(θ/2)
+ 1 +
1
cos
4
(θ/2)
(24)
The physical origin of each of the terms in (23) [before we simplify with trigonometric
identities] to get to (24) is clear. The first term strongly favors forward scattering due
to the photon propagator ∼ 1/k
2
blowing up at k ∼ 0. The third term is required by the
indistinguishability of the two outgoing electrons: the scattering must be symmetric under
θ → π − θ, since experimentalists can’t tell whether a particular incoming electron has
scattered forward or backward. The second term is the most interesting of all: it comes from
quantum interference. If we had mistakenly thought that electrons are bosons and taken
the plus sign in (6), the second term in f(θ)would come with a minus sign. This makes
a big difference: for instance, f(π/2) would be 5 − 8 + 5 = 2 instead of 5 + 8 + 5 = 18.
Since the conversion of a squared probability amplitude to a cross section is conceptually
the same as in nonrelativistic quantum mechanics (divide by the incoming flux, etc.), I
will relegate the derivation to an appendix and let you go the last few steps and obtain the
differential cross section as an exercise:
dσ
d
=
α
2
8E
2
f(θ) (25)
with the fine structure constant α ≡ e
2
/4π ≈ 1/137.

II.6. Scattering and Gauge Invariance | 139
An amazing subject
When you think about it, theoretical physics is truly an amazing business. After the
appropriate equipments are assembled and high energy electrons are scattered off each
other, experimentalists indeed would find the differential cross section given in (25). There
is almost something magical about it.
Appendix: Decay rate and cross section
To make contact with experiments, we have to convert transition amplitudes into the scattering cross sections
and decay rates that experimentalists actually measure. I assume that you are already familiar with the physical
concepts behind these measurements from a course on nonrelativistic quantum mechanics, and thus here we
focus more on those aspects specific to quantum field theory.
To be able to count states, we adopt an expedient probably already familiar to you from quantum statistical
mechanics, namely that we enclose our system in a box, say a cube with length L on each side with L much larger
than the characteristic size of our system. With periodic boundary conditions, the allowed plane wave states e
i p
.
x
carry momentum
p =
2π
L
(n
x
, n
y
, n
z
) (26)
where the n
i
’s are three integers. The allowed values of momentum form a lattice of points in momentum space
with spacing 2π/Lbetween points. Experimentalists measure momentum with finite resolution, small but much
larger than 2π/L. Thus, an infinitesimal volume d
3
p in momentum space contains d
3
p/(2π/L)
3
=Vd
3
p/(2π)
3
states with V = L
3
the volume of the box. We obtain the correspondence
d
3
p
(2π)
3
f(p)↔
1
V
p
f(p) (27)
In the sum the values of p ranges over the discrete values in (26). The correspondence (27) between continuum
normalization and the discrete box normalization implies that
δ
(3)
( p −p
) ↔
V
(2π)
3
δ
p p
(28)
with the Kronecker delta δ
p p
equal to 1 if p =p
and 0 otherwise. One way of remembering these correspondences
is simply by dimensional matching.
Let us now look at the expansion (I.8.17) of a complex scalar field
ϕ(x, t) =
d
3
k
(2π)
3
2ω
k
[a(
k)e
−i(ω
k
t−
k
.
x)
+ b
†
(
k)e
i(ω
k
t−
k
.
x)
] (29)
in terms of creation and annihilation operators. Henceforth, in order not to clutter up the page, I will abuse
notation slightly, for example, dropping the arrows on vectors when there is no risk of confusion. Going over to
the box normalization, we replace the commutation relation [a(k), a
†
(k
)] = δ
(3)
(
k −
k
) by
[a(k), a
†
(k
)] =
V
(2π)
3
δ
k
k
(30)
We now normalize the creation and annihilation operators by
a(k) =
V
(2π)
3
1
2
˜a(k) (31)
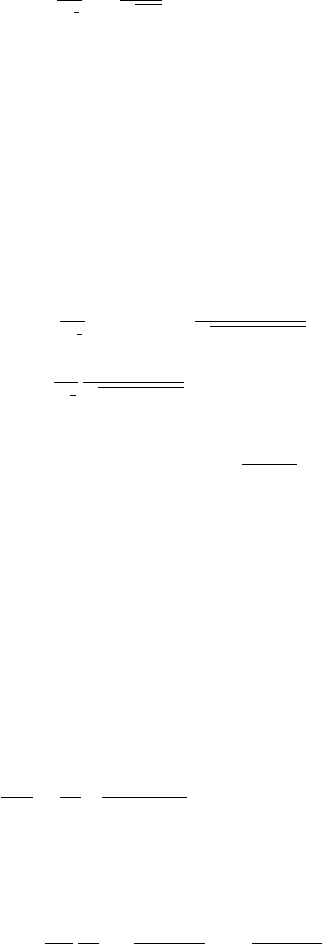
140 | II. Dirac and the Spinor
so that
[˜a(k), ˜a
†
(k
)] =δ
k, k
(32)
Thus the state |
k≡˜a
†
(
k)|0 is properly normalized:
k|
k=1. Using (27) and (31), we end up with
ϕ(x) =
1
V
1
2
k
1
2ω
k
( ˜ae
−ikx
+
˜
b
†
e
ikx
) (33)
We specified a complex, rather than a real, scalar field because then, as you showed in exercise I.8.4, a
conserved current can be defined with the corresponding charge Q =
d
3
xJ
0
=
d
3
k(a
†
(k)a(k) −b
†
(k)b(k)) →
k
( ˜a
†
(k) ˜a(k) −
˜
b
†
(k)
˜
b(k)). It follows immediately that
k|Q |
k=1, so that for the state |
kwe have one particle
in the box.
To derive the formula for the decay rate, we focus, for the sake of pedagogical clarity, on a toy Lagrangian
L = g(η
†
ξ
†
ϕ + h.c.) describing the decay ϕ → η + ξ of a meson into two other mesons. (As usual, we display
only the part of the Lagrangian that is of immediate interest. In other words, we suppress the stuff you have long
since mastered: L = ∂ϕ
†
∂ϕ − m
ϕ
ϕ
†
ϕ +
...
and all the rest.)
The transition amplitude p, q|e
−iHT
|
k is given to lowest order by A = ip, q|
d
4
x(gη
†
(x)ξ
†
(x)ϕ(x)) |
k.
Here we use the states we “carefully” normalized above, namely the ones created by the various “analogs” of ˜a
†
.
(Just as in quantum mechanics, strictly, we should use wave packets instead of plane wave states. I assume that
you have gone through that at least once.) Plugging in the various “analogs” of (33), we have
A = ig(
1
V
1
2
)
3
p
q
k
1
2ω
p
2ω
q
2ω
k
d
4
xe
i(p
+q
−k
)
p, q|˜a
†
(p
) ˜a
†
(q
) ˜a(k
) |
k
= ig
1
V
3
2
1
2ω
p
2ω
q
2ω
k
(2π)
4
δ
(4)
(p + q − k)
(34)
Here we have committed various minor transgressions against notational consistency. For example, since
the three particles ϕ, η, and ξ have different masses, the symbol ω represents, depending on context, different
functions of its subscript (thus ω
p
=
p
2
+ m
2
η
, and so forth). Similarly, ˜a(k
) should really be written as ˜a
ϕ
(k
),
and so forth. Also, we confound 3- and 4-momenta. I would like to think that these all fall under the category of
what the Catholic church used to call venial sins. In any case, you know full well what I am talking about.
Next, we square the transition amplitude A to find the transition probability. You might be worried, because
it appears that we will have to square the Dirac delta function. But fear not, we have enclosed ourselves in a box.
Furthermore, we are in reality calculating p, q|e
−iHT
|
k, the amplitude for the state |
k to become the state
|p, q after a large but finite time T . Thus we could in all comfort write
[(2π)
4
δ
(4)
(p + q − k)]
2
= (2π)
4
δ
(4)
(p + q − k)
d
4
xe
i(p+q−k)x
= (2π)
4
δ
(4)
(p + q − k)
d
4
x = (2π)
4
δ
(4)
(p + q − k)V T
(35)
Thus the transition probability per unit time, aka the transition rate, is equal to
|A|
2
T
=
V
V
3
1
2ω
p
2ω
q
2ω
k
(2π)
4
δ
(4)
(p + q − k)g
2
(36)
Recall that there are Vd
3
p/(2π)
3
states in the volume d
3
p in momentum space. Hence, multiplying the number
of final states (V d
3
p/(2π)
3
)(V d
3
q/(2π)
3
) by the transition rate |A|
2
/T , we obtain the differential decay rate of
a meson into two mesons carrying off momenta in some specified range d
3
p and d
3
q:
d =
1
2ω
k
V
V
3
V
d
3
p
(2π)
3
2ω
p
V
d
3
q
(2π)
3
2ω
q
(2π)
4
δ
(4)
(p + q − k)g
2
(37)
Yes sir, indeed, the factors of V cancel, as they should.
To obtain the total decay rate we integrate over d
3
p and d
3
q. Notice the factor 1/2ω
k
: the decay rate for a
moving particle is smaller than that of a resting particle by a factor m/ω
k
. We have derived time dilation, as we
had better.
II.6. Scattering and Gauge Invariance | 141
We are now ready to generalize to the decay of a particle carrying momentum P into n particles carrying
momenta k
1
,
...
, k
n
. For definiteness, we suppose that these are all Bose particles. First, we draw all the relevant
Feynman diagrams and compute the invariant amplitude M. (In our toy example, M = ig.) Second, the transition
probability contains a factor 1/V
n+1
, one factor of 1/V for each particle, but when we squared the momentum
conservation delta function we also obtained a factor of VT, which converts the transition probability into a
transition rate and knocks off one power of V , leaving the factor 1/V
n
. Next, when we sum over final states, we
have a factor Vd
3
k
i
/((2π)
3
2ω
k
i
) for each particle in the final state. Thus the factors of V indeed cancel.
The differential decay rate of a boson of mass M in its rest frame is thus given by
d =
1
2M
d
3
k
1
(2π)
3
2ω(k
1
)
...
d
3
k
n
(2π)
3
2ω(k
n
)
(2π)
4
δ
(4)
P −
n
i=1
k
i
|M|
2
(38)
At this point, we recall that, as explained in chapter II.2, in the expansion of a fermion field into creation and
annihilation operators [see (II.2.10)], we have a choice of two commonly used normalizations, trivially related
by a factor (2m)
1
2
. If you choose to use the “rest normalization" so that spinors come out nice in the rest frame,
then the field expansion contains the normalization factor (E
p
/m)
1
2
instead of the factor (2ω
k
)
1
2
for a Bose
field [see (I.8.11)]. This entails the trivial replacement, for each fermion, of the factor 2ω(k) = 2
k
2
+ m
2
by
E(p)/m =
p
2
+ m
2
/m. In particular, for the decay rate of a fermion the factor 1/2M should be removed. If
you choose the “any mass renormalization,” you have to remember to normalize the spinors appearing in M
correctly, but you need not touch the phase space factors derived here.
We next turn to scattering cross sections. As I already said, the basic concepts involved should already be
familiar to you from nonrelativistic quantum mechanics. Nevertheless, it may be helpful to review the basic
notions involved. For the sake of definiteness, consider some happy experimentalist sending a beam of hapless
electrons crashing into a stationary proton. The flux of the beam is defined as the number of electrons crossing
an imagined unit area per unit time and is thus given by F = nv, where n and v denote the density and velocity
of the electrons in the beam. The measured event rate divided by the flux of the beam is defined to be the cross
section σ , which has the dimension of an area and could be thought of as the effective size of the proton as seen
by the electrons.
It may be more helpful to go to the rest frame of the electrons, in which the proton is plowing through the
cloud of electrons like a bulldozer. In time t the proton moves through a distance vt and thus sweeps through
a volume σvt, which contains nσ vt electrons. Dividing this by t gives us the event rate nvσ .
To measure the differential cross section, the experimentalist sets up, typically in the lab frame in which the
target particle is at rest, a detector spanning a solid angle d = sin θdθdφ and counts the number of events per
unit time.
All of this is familiar stuff. Now we could essentially take over our calculation of the differential decay rate
almost in its entirety to calculate the differential cross section for the process p
1
+p
2
→k
1
+k
2
+
...
+k
n
. With
two particles in the initial state we now have a factor of (1/V)
n+2
in the transition probability. But as before, the
square of the momentum conservation delta function produces one power of V and counting the momentum
final states gives a factor V
n
, so that we are left with a factor of 1/V. You might be worried about this remaining
factor of 1/V, but recall that we still have to divide by the flux, given by |v
1
−v
2
|n. Since we have normalized to
one particle in the box the density n is 1/V. Once again, all factors of V cancel, as they must.
The procedure is thus to draw all relevant diagrams to the order desired and calculate the Feynman amplitude
M for the process p
1
+p
2
→k
1
+k
2
+
...
+k
n
. Then the differential cross section is given by (again assuming
all particles to be bosons)
dσ =
1
|v
1
−v
2
|2ω(p
1
)2ω(p
2
)
d
3
k
1
(2π)
3
2ω(k
1
)
...
d
3
k
n
(2π)
3
2ω(k
n
)
(2π)
4
δ
(4)
p
1
+ p
2
−
n
i=1
k
i
|M|
2
(39)
We are implicitly working in a collinear frame in which the velocities of the incoming particles, v
1
and v
2
,
point in opposite directions. This class of frames includes the familiar center of mass frame and the lab frame (in
which v
2
=0). In a collinear frame, p
1
= E
1
(1, 0, 0, v
1
) and p
2
= E
2
(1, 0, 0, v
2
), and a simple calculation shows
that ((p
1
p
2
)
2
− m
2
1
m
2
2
) = (E
1
E
2
(v
1
− v
2
))
2
. We could write the factor |v
1
−v
2
|E
1
E
2
in dσ in the more invariant-
looking form ((p
1
p
2
)
2
− m
2
1
m
2
2
)
1
2
, thus showing explicitly that the differential cross section is invariant under
Lorentz boosts in the direction of the beam, as physically must be the case.
