Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань
Подождите немного. Документ загружается.


Елементи теорії похибок вимірювань
243
П
т
=
±
[4
2
]
(4.1)
п
На основі досліджень випадкових похибок встановлено такі емпіричні
залежності:
Середня квадратична похибка є найкращим критерієм для оцінки точності
вимірювань. Вона має такі переваги над середньою та ймовірною похибками:
1). Середня квадратична похибка є досить чутливою мірою точності тому,
що на її величину сильніше впливають великі за абсолютною величиною випадкові
похибки, що в основному і визначають надійність результатів вимірювань.
2). Середня квадратична похибка вже при деякій відносно не дуже великііі
кількості вимірювань набуває сталого значення і в подальшому при збільшенні
кількості вимірювань змінюється дуже повільно.
3). За величиною середньої квадратичної похибки можна знайти граничну
похибку, тобто таке найбільше за абсолютною величиною значення випадкової
похибки, яке ще може з'явитися при даних умовах вимірювань. Потрійна середня
квадратична похибка приймається за граничну, тобто
А = 3 т. (4.6)
гран '
4). Знаючи середні квадратичні похибки якихось величин, можна легко визначити
середні квадратичні похибки інших величин, функціонально пов'язаних із ними.
Розрізняють абсолютні та відносні похибки. Істинну похибку А, середню 0,
ймовірну рта середню квадратичну т називають абсолютними похибками.
Часто при вимірюванні лінійних величин та площ використовують відносні
похибки. Це безрозмірні величини, які обчислюються відношенням абсолютних
похибок до виміряного значення якоїсь величини. Розглянемо виміряне значення .v
довільної величини. Тоді
(4.4)
2
(4.5)
А
відносна істинна похибка,
відносна середня похибка,
х

> Розділ IV
- відносна середня квадратична похибка,
- відносна ймовірна похибка.
§ 4.6. Розподіл ймовірностей випадкових похибок
іультати вимірювань будь-якої фізичної величини є випадковими, оскільки
іачити їх неможливо. Розглянемо довільну неперервну випадкову величину X
юрмальний закон розподілу, який є граничним законом розподілу як
грвних, так і дискретних випадкових величин, тобто таким, до якого
ють всі інші закони при певних умовах. Ці умови складаються тоді, коли
ювана випадкова величина містить суму багатьох інших випадкових
ГІН, що мають відмінні від нормального розподіли. У природі така ситуація
в більшості випадків і тому нормальний закон або його комбінації
чаються найчастіше.
[ференціальна функція даного розподілу, або функція густини має вигляд
/(*) =
•
(х-т)
2
J „ 2а
2
уІ2Й а
^-математичне сподівання та дисперсія відповідно (параметри розподілу),
домо, що "найкращою оцінкою" математичного сподівання є середнє
іетичне. Тому для випадкової величини X, якщо вона є істинною випадковою
ікою, математичне сподівання дорівнює нулеві за четвертою властивістю
кових похибок (див. §4.4) і функція густини запишеться так:
1
f(A) = -=L е
V2TT а
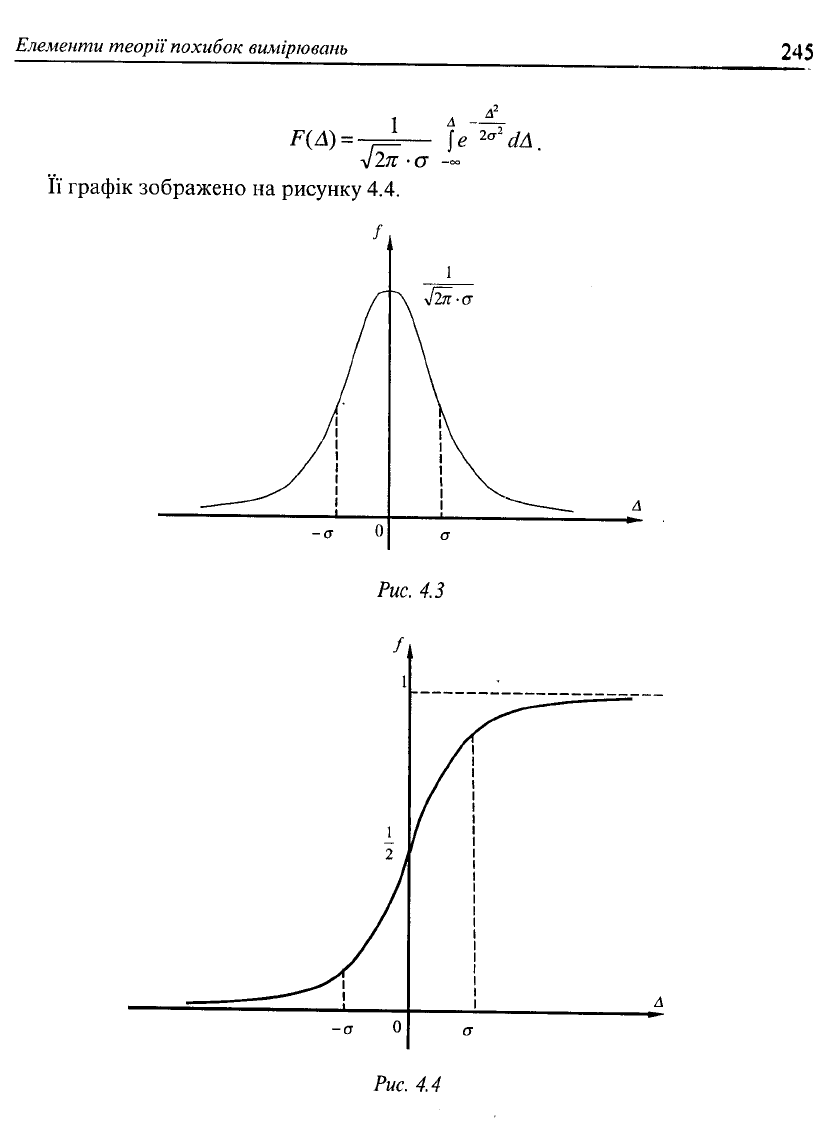
)афік цієї функції зображено рисунком 4.3.
вигляду кривої та виразу дляДЛ) видно, що даний розподіл є симетричним
»сно осі ординат, на якій досягається найбільше значення густини
=
-рі— . Абсциси точок перегину кривої відповідають значенням А = ±сг.
у]2л
-
а
тегральна функція нормального розподілу істинних випадкових похибок А
гакою:
Елементи теорії похибок вимірювань
245
F(A)
=
-=L— ]e~
2
°
2
dA.
V2л о
Рис.
4.4

> Розділ IV
з рисунка 4.4 видно, що центром симетрії інтегральної кривої розподілу
нних випадкових похибок є точка
f
1
Л
°
;
2
. Абсциси точок перегину
ішаються ті ж самі, що і для кривої густини розподілу.
§ 4.7. Дослідження похибок на випадковість
3
еально існуючі випадкові похибки вимірювань підлягають нормальному
>ну розподілу. Але не всякі похибки вимірювань бувають випадковими. Тому
якає необхідність дослідження рядів похибок вимірювань на випадковість,
до похибки вимірювань якоїсь фізичної величини є випадковими, то
снуватимуться співвідношення (4.4) та (4.5). Дані співвідношення є тільки
Зхідними умовами випадковості, тобто вони завжди виконуватимуться, якщо
ибки вимірювань є випадковими. Але виконання наведених співвідношень не
статніми умовами, тобто вони можуть виконуватись для похибок вимірювань,
не задовільняють властивості випадковості. У зв'язку з цим проводяться
альші дослідження похибок вимірювань досліджуваних рядів, а саме
звіряється нульова гіпотеза Я
0
про їх нормальний закон розподілу. Для цього
рібно:
1) побудувати інтервальний статистичний ряд розподілу похибок вимірювань
ідповідний йому дискретний статистичний ряд;
2) за даними побудованих рядів обчислити оцінки параметрів нормального
поділу, а саме середнє вибіркове та вибіркову дисперсію;
3) знайти всі значення функції густини нормального розподілу за даними
кретного статистичного ряду і на їх основі побудувати криву розподілу та
ограму відносних частот на одному графіку;
4) із використанням критерію Пірсона х
г
перевірити справедливість
рмульованої нульової гіпотези Я
0
, якщо альтернативною гіпотезою Я, буде
ічне заперечення нульової гіпотези, тобто досліджуваний ряд похибок
іірювань не підлягає нормальному закону розподілу.
Приклад. Задано ряд істинних похибок результатів вимірювань якоїсь
ичини 4, 13, 13,-8,21, 11, 16, 13, 1,-2,-14, 8, 11,2, 1,-2, 13,-5,9, 8, 11,-6, -21,
-8, 7, -11,4, 8, 8,23, -4,9, -22, -5, -23,15,14,17, -12,1, -11,10, -11, 7,16, -20, 8, 23,
9,-10, 1,-29.
Потрібно визначити, чи наведені похибки є випадковими, чи якогось іншого
актеру.
Спочатку перевіримо необхідні умови випадковості.
1. Обчислимо середню квадратичну похибку

Елементи теорії похибок вимірювань
247
8682
=±1
п V 54
2. Знайдемо середню похибку
в=М
|]
=
586
п 54
4. Побудуємо абсолютний варіаційний ряд наведених похибок 1, 1, 1, 1,2,
2,2,4,4,4, 5,5,6, 7, 7, 8,8,8,8, 8, 8, 8,9, 9,9, 10, 10,11, 11,11, 11, 11, 11, 12, 13, 13,
13, 13, 13, 14, 14, 14, 15, 16, 16, 17, 20, 21, 21, 22, 23, 23, 23, 29, із якого отримаємо
ймовірну похибку
10 +
11
...
р = = 10,5
2
4 2
4. Перевіримо виконання умов 0 =
—
m і р ~—т, тобто
*=ІМ^ = о,856,^ = ^ = 0,829.
т 12,67 ' т 12,67
Як видно з результатів обчислень, вони не виконуються. Дані умови є
необхідними і вони не виконуються. Тому подальші дослідження можна не
проводити, тобто наведений ряд похибок не є випадковим. Але на даному
прикладі покажемо як проводити подальші дослідження на випадковість, тобто
перевірку достатніх умов випадковості.
5. Обчислимо граничну похибку
Л
гр
=3-т = 3-(±12,67) = ±38,34,
яку не перевищують похибки з наведеного ряду, та середнє арифметичне похибок
— = — = 1,78 (для випадкових похибок — = 0).
«54 п
6. За формулою Стерджеса знайдемо кількість інтервалів г та їх довжину її
г =
1
+ 3,322
•
lg
п
=
1
+ 3,322
•
lg 54 « 7 ,
Д
=
4П,Х-Апі,
=
23 + 29
=
52
г 7 7
та побудуємо інтервальний статистичний ряд розподілу похибок, зображений
таблицею 4.1,

> Розділ IV
Таблиця 4.1
ІІІ
Д+і)
[-29; -21,6)
[-21,6;-14,2)
[-14,2;-6,8) [-6,8; 0,6)
[0,6; 8)
[8; і->,4)
[15,4; 23]
Єі
-25,3
-17,9 -10,5
-3,1
4,3 11,7
19,2
к,-
3
2
9
6 9
19 6
Р*
0,05
0,04 0,17
0,11
0,17 0,35 0,11
:. - частота /-го інтервалу (кількість похибок, які потрапляють на даний інтервал);
' к- —
=
—
L
відносна частота /-го інтервалу;
є.
- середина /-го інтервалу; і = 1,7.
п '
7. За даними інтервального статистичного ряду розподілу похибок обчислимо
еднє вибіркове А , вибіркову дисперсію S
2
та вибіркове середнє квадратичне
хилення
А = І є і
• р*
= -25,3
•
0,05 -17,9
•
0,04 -10,5
•
ОД
7
-
3,1 -0,11
+
(=і
+
4,3 • 0,17
+11,7
-0,35
+ 19,2
• 0,11
= 2,84;
S
2
= £є,
2
• р*
-А
1
=640,09-0,05 + 320,41-0,04 + 110,25-0,17
г
у,61-0,11 +
+18,49
• 0,17
+136,89
•
0,35 + 368,64
• 0,11
- (2,84)
2
= 156,22 - 8,07 = 148,15 ;
s = yfs
1
= 12,17 .
£ -А —
8. Знайдемо нормуючі аргументи = (/ = 1,7) функції густини нормального
S
-(х-т)
2
зподілу /(х) = —-== е
2
°
2
та за таблицею (див. Додаток, табл.
1)
знайдемо її
о лі 2л
ачення. Результати обчислень значень нормуючих аргументів та відповідних їм
ачень функції густини занесемо в таблицю 4.2.
Таблиця 4.2
є
І
-25,3
-17,9 -10,5
-3,1
4,3 11,7 19,2
ti
-2,31
-1,70 -1,10 -0,49
0,12
0,73
1,34
At)
0,0277
0,0941 0,2178
0,3538 0,3961 0,3056 0,1626
9. Побудуємо на одному графіку гістограму відносних частот та криву функції
'стини нормального розподілу (див. Рис.4.5)
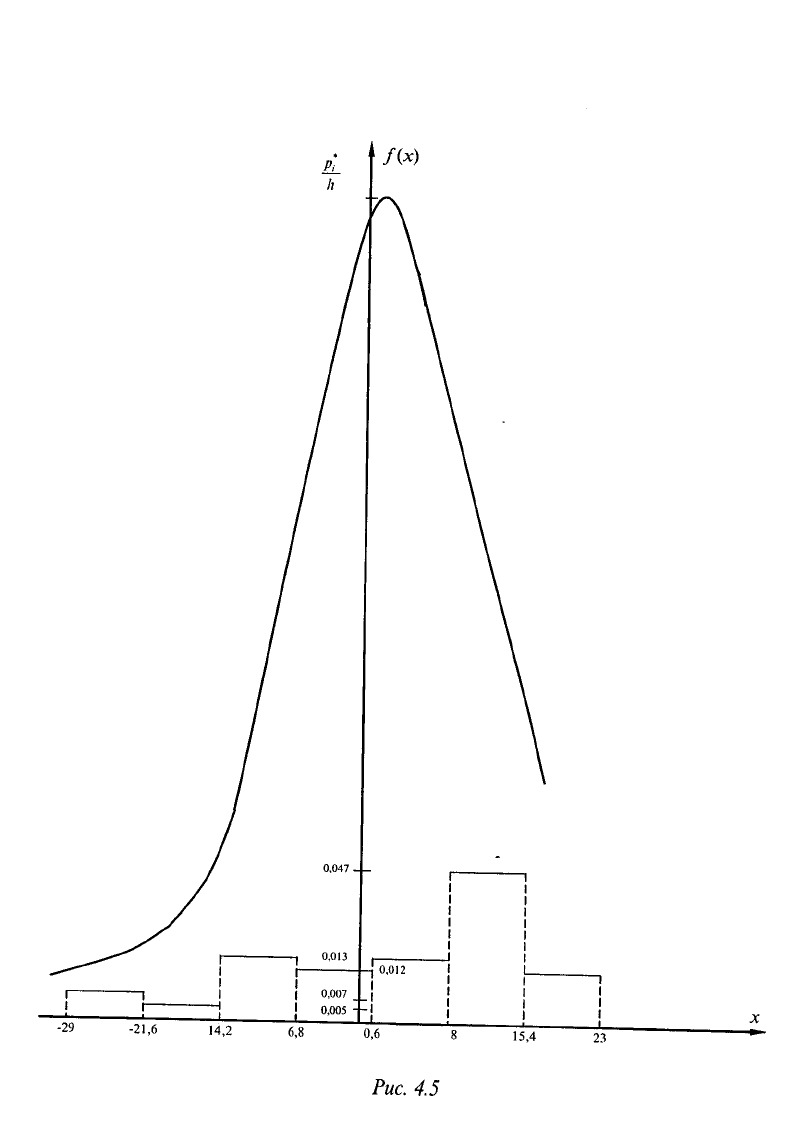
Рис. 4.5

> Розділ IV
зевіримо нульову гіпотезу Н
0
, яка твердить що наведений емпіричний
(іл є нормальним. Альтернативною гіпотезою Н
г
буде логічне заперечення
юї гіпотези Н
0
, тобто даний емпіричний розподіл не є нормальним.
Ї перевірки нульової гіпотези Н
0
використаємо критерій Пірсона
Ф
0
(
2
/+і) ~ 4
Z
)
~~
ймовірність потрапляння значення істинної похибки на
гервал; Ф
0
(г) - функція Лапласа; z
i
=
———
.
S
очатку обчислимо значення z., ймовірності р. та п-р. (і -1,7)
п = Ік, =3 + 2 +
9
+
6
+
19
+ 6 = 54;
/=і
-
29
-
2
'
84
.-2,616; z
2
. -
21
'
6
-
2
'
84
.-2,008;
Zj
= .
40
„
12,17 12,17
3
12,17
= -
6
'
8
"
2
'
84
= -0,792; z
5
= -°'
6
-
2
'
84
= -0,184 ; z
6
=
= 0>424
.
12,17
5
12,17
6
12,17
.5,4-2,84
=
23-2j4
7
12,17
8
12,17
Рі =Ф
0
(г
2
) - Ф
0
(z,) = -Ф
0
(2,008) + Ф
0
(2,616) = 0,4956 - 0,4778 = 0,018;
р
2
=Ф
0
(
2з
)-Ф
0
(
г2
)
=
-Ф
0
(1,400) + Ф
0
(2,008) = 0,4778 - 0,4192 = 0,059;
Рг =
ф
о ) -
ф
о (
г
з) = (0,792) + Ф
0
(1,400) = 0,4192 - 0,2852 = 0,134;
р
4
= Ф
0
(z
s
) - Ф
0
(z
4
) = -Ф
0
(0,184) + Ф
0
(0,792) = 0,2852 - 0,0714 = 0,214;
Р5
=Ф
0
(
2б
)-Ф
0
(
2$
)
=
Ф
0
(0,424) + Ф
0
(0,184) = 0,1628 - 0,0714 = 0,234;
Рб
= Ф
0
(z
7
) - Ф
0
(z
6
) = Ф
0
(1,032) - Ф
0
(0,424) = 0,3485 - 0,1628 = 0,186;
Рі
= Ф
0
(z
8
) - Ф
0
(z
7
) = Ф
0
(1,656) - Ф
0
(1,032) = 0,4515 - 0,3485 = 0,103;
пр
х
=54-0,018 = 1; пр
2
=54-0,059 = 3; пр
г
= 54-0,134 = 7;
пр
4
=54-0,214 = 12; пр
5
=
54-0,234 = 13; пр
6
=54-0,136 = 10;
пр
п
=54-0,103 = 6.
гепер знайдемо емпіричне значення критерію х
2

Елементи теорії похибок вимірювань
251
2
= 4 + - + - +
3
+ — + —+ 0 = 4 + 0,333 + 0,571 +
3
+
1,231
+
8,1
= 17,235
З 7 13 10
З 7
16 81
Задавши рівень значущості а = 0,05 та визначивши кількість ступенів
довільності г = 7 - 3 = 4, за таблицею критичних точок розподілу х
2
(див. Додаток,
табл.З), знаходимо точку правобічної критичної області #^,(0,05; 4) = 9,488.
Оскільки хІр < Хемп'
то
нульова гіпотеза Н
0
про нормальний розподіл похибок
результатів вимірювань відхиляється і на цьому завершується перевірка достатніх
умов випадковості.
Часто на практиці буває так, що шукана величина не може бути виміряна
безпосередньо. Її значення можна отримати через безпосередньо виміряні
величини, якщо шукана величина і дані величини є функціонально пов'язані.
Оскільки значення безпосередньо виміряних величин є отримані з якимись
похибками, то і значення шуканої величини, як функції від них, також буде
отримано з якоюсь похибкою. У зв'язку з цим виникає задача визначення середньої
квадратичної похибки функції виміряних величин.
Розглянемо X, Y,..., U- істинні значення вимірюваних величин, а х,, х
2
,..., х ,
у
х
, у
2
, ..., у
т
, ..., И|, и
2
, ..., и
/
- виміряні значення п - разів величини X, т - разів
величини Y, І- разів величини U.
Знайдемо істинні похибки даних величин. Вони будуть такими:
Au
k
= и
к
-U, к = \,1 .
Розглянемо деяку функцію F, аргументами якої будуть незалежні величини
х,у, ..., и, отримані зі спостережень із істинними похибками (4.7), тобто
§ 4.8. Середні квадратичні похибки функцій
незалежно виміряних величин
Ах і = х,- - X, і =
1,
п,
&У, = Уі - У, І = \т,
(4.7)
F = F{x, у, ..., и).

>
Розділ IV
Для простоти викладу обмежимось двома аргументами, тобто функцію F
цамо так:
F=F(x,y). (4.8)
Припустимо, що функція F= F{x, у) є неперервною разом зі своїми частковими
хідними до {р + 1) порядку в деяких околах точок M
jj
(x
p
у^. Тоді дану функцію
:
F(x, у) можна зобразити сумою багаточленар-то порядку за степенями (х - х)
(у - ур і деякого залишкового члена, розклавши її в ряд Тейлора. Таких
Зражень буде n-m. Запишемо їх.
F(x, у) = F{x
t
,у
}
) + F'
x
(х,-,
у j ) (х - х,-) + Fy(Xi, у
}
)(y-yj)
+
+ , ) - ^ )
2
+ 2 ^ ) - )
(J^
- ^) + , ^) - ^ )
2
3
+
+ ^[K
x
Ax
i
,y
J
)(x-x
i
)
i
+ 3F;
xy
(x
i
,y
J
)(x-x
i
)
2
(y-y
j
)+ (4.9)
З F
xyy
(х,, у j) (х -х,.) (у - у j )
2
+ F
yyy
{
х,-
, у j) (у - у
}
)
3
]
+... + R
р
( х, у), / = 1,
п
, j = 1, m,
R (х, у) - залишковий член розкладу.
ббмежившись лінійними членами розкладу, вирази (4.9) запишемо так:
г
(х, у) - F(Xj ,yj) +
F'
x
(х,., у j )(х - х,.) + F'
y
(х,-
,yj)(y- у j), і-Yji, j = Yjn. (4.10)
Але співвідношення
F(x
i
,y
j
)-F(x,y)^AF
iJ
, (4.11)
стинними похибками функції F= F(x, у). Тоді формули (4.10) перепишемо
AFy =
F'
x
(х
і
, у j )Ах
і
+ F
y
(х,, у j )Ayj, i = = (4.12)
Праву та ліву частини співвідношень (4.12) піднесемо до квадрату. У результаті
римаємо
A
2
F
ij
=F'
2
{x
i
,y
j
)A
2
x
i
+2F'
x
(x
i
,y
j
)F;(x
i
,y
j
)Ax
i
Ay
j
+F;(x
i
,y
j
)A
2
y
i
,
_ _ (4.13)
i = l,n,j = l,m-
Просумувавши вирази (4.13) за індексами і та у'та поділивши на їх кількість,
(ержимо
-І Z^Fg = — ±l[F:
x
\x
i
,y
j
)A
2
x
i
+2F'
x
{x
i
,y
j
)F;<
<
x
i
,y
j
)Ax
i
Ay
j
+F;
2
{x
i
,y
j
)A
2
y
j
]. (4.14)
m
і=і j~\
nwi
/=і y=i
