Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань

Подождите немного. Документ загружается.

Елементи математичної статистики

І'Л

отриманих результатів за рахунок інструментів та за рахунок спостерігачів, маючи

на увазі, що інструменти можуть бути неякісними або погано вивіреними, а

виконавці недостатньо підготовленими.

Ідея такого двофакторного дисперсійного аналізу полягає в тому, щоб

розкласти загальну дисперсію на складові, які відповідатимуть припущенням

щодо двох зазначених факторів. Вихідні дані наведені в таблиці 3.10.

Таблиця .110

Фактор А

(вплив

інструм.)

Фактор В (вплив спостерігача)

Фактор А

(вплив

інструм.)

і В,

Вг

в.

X,:

А,

Хп

ху

Хи

X,.

Х2\ Хгг Ху

хг.

А, Х,\

ха

Ху

Xjv

X,,

j X

Х„

х*

Х.2

X.j

Х„

Середні в групах х

* , х*

- та загальне середнє д:

обчислюються так:

- _ 1 ' _ _ 1 ' _ 1 г »

і* - 7 L

i/,

*j - - L

ij ; = — £ •

Сума квадратів зображається у вигляді

Q = H(x

*,)

;=1./=]

= X £ (Ху - х

- x»j

х,„

- х», + x*j - х».) =

r=l

j=1

— 2

— 7

r V

— — — ->

^V-'ZiXj, -x,») +r-£(x„.-X»») +£ £(x,

-X,.»-x„, +x,„)

/=1 ;=i /=17=1

(3.87)

де Q

- сума квадратів різниць між середніми у рядках та загальним середнім,

характеризує зміну дисперсії за фактором А;

-сума квадратів різниць між середніми у стовпчиках та загальним середнім,

характеризує зміну дисперсії за фактором В;

- залишкова сума квадратів, яка характеризує невраховані фактори;

Q - загальна сума квадратів.

> Розділ

ідно з цими величинами оцінки дисперсії будуть

: _ 1

" - 2 Q

rv -1 ?і

—[

оцінка загальної дисперсії, (3.88)

1 r

= r vX(x,*-**») = г - оцінка дисперсії за фактором А, (3.89)

г -1 /=1 г

— 1

1 v _ _ 2 Q

~ -х**) -- - - оцінка дисперсії за фактором В, (3.90)

— 1

/=1 V

— 1

1 ^

, ^

ч2

_ Єз

(г-1)(и-1)Ш

[Xij

Хі

*~(

-1)0,-1) -°

цінка (3

91)

кової дисперсії.

величини мають х

~розподіл з к = (rv-1), к

= (г

-1), к

(v-1), к

= (r

- l)(t>-1)

ями довільності відповідно.

цвофакторному аналізі для встановлення впливу факторів А та В на

та S

^ ТУ ГМ .1

ГЛ1V

і^Л 7 П \ /Т І

жувану величину порівнюють оцінки дисперсії S

та 5

за факторами А і В

кою залишкової дисперсії S

. F-критерії будуть мати вигляд

бі . Єз

^ г-Г (r-l)-(u-l) 5

/Г 6з ^ ^2

и-Г (r-l).(w-l) s

римані значення F^ та F

порівнюють із табличним F

за вибраним рівнем

цості а (або q%, тобто а = q/100).

що F

> F

та F

> F

, то нульова гіпотеза H

про рівність математичних

ань відхиляється і вплив факторів не вважається суттєвим,

иклад 15. У таблиці 3.11 наведено результати вимірювань базису

уляції трьома мірними стрічками. Отримано по три числових значення

ни базису для кожної стрічки.

івиться таке запитання: чи можна вважати, що отримані за допомогою

стрічок результати мають однакові систематичні похибки?

аблиці 3.12 обчислюємо необхідні складові дисперсії,

ходимо значення критерія Фішера

123,7

Елементи математичної статистики

І'Л

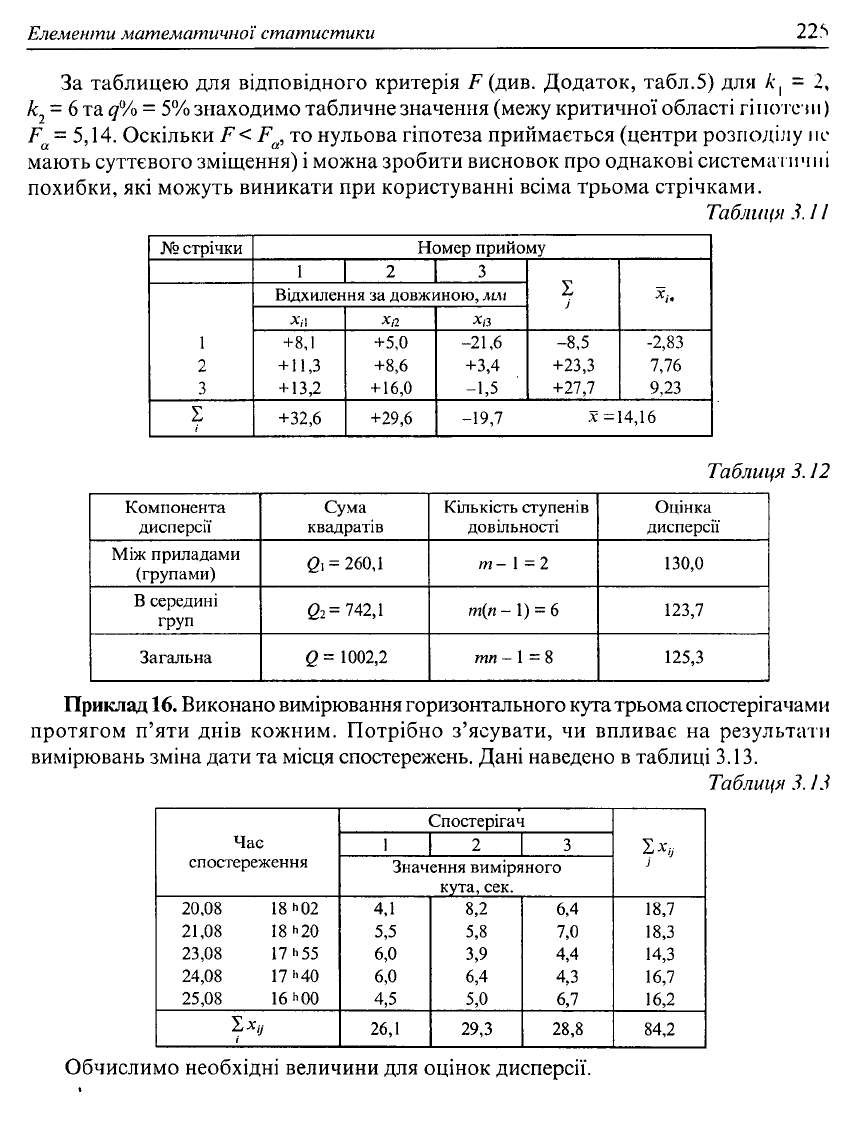
За таблицею для відповідного критерія ^(див. Додаток, табл.5) для А-, = 2,

= 6 та q% = 5% знаходимо табличне значення (межу критичної області гіпотези)

5,14. Оскільки F< F

, то нульова гіпотеза приймається (центри розподілу не

мають суттєвого зміщення) і можна зробити висновок про однакові систематичні

похибки, які можуть виникати при користуванні всіма трьома стрічками.

Таблиця3. І

№ стрічки

Номер прийому

1 2 3

Хі.

Відхилення за довжиною, лш

Хі.

Хц

ха

Хі.

+8,1 +5,0 -21,6 -8,5 -2,83

2 + 11,3

+8,6 +3,4 +23,3 7,76

+ 13,2 + 16,0

-1,5

+27,7 9,23

+32,6 +29,6 -19,7

х =

14,16

Таблиця 3.12

Компонента

дисперсії

Сума

квадратів

Кількість ступенів

довільності

Оцінка

дисперсії

Між приладами

(групами)

Q, = 260,1 т - 1=2 130,0

В середині

груп

22= 742,1 т(п - 1) = 6

123,7

Загальна Q = 1002,2

ти - 1=8

125,3

Приклад

16.

Виконано вимірювання горизонтального кута трьома спостерігачами

протягом п'яти днів кожним. Потрібно з'ясувати, чи впливає на результати

вимірювань зміна дати та місця спостережень. Дані наведено в таблиці 3.13.

Таблиця 3.13

Спостерігач

Час

1 2

спостереження

Значення виміряного

кута,сек.

20,08 18

4,1

8,2 6,4

18,7

21,08 18

20 5,5 5,8 7,0

18,3

23,08 17

6,0 3,9 4,4

14,3

24,08 17

40 6,0 6,4

4,3 16,7

25,08 16 ^00

4,5 5,0

6,7 16,2

26,1

29,3 28,8 84,2

Обчислимо необхідні величини для оцінок дисперсії.

> Розділ

Таблиця 3.14

Компонента

дисперсії

Сума

квадратів

Кількість ступенів

довільності

Оцінка

дисперсії

Між датами

;гюстережень

a -x.,f

2. =4,2

= 4

1,05

Між

спостері-

гачами

=r-hx.j-X..)

J" 1

62=1,2

U-l =2

0,60

Залишкова

ll(x

-x

.-x.

+x..)

= 16,0

(г-1)(и -1) = 8 2,00

Загальна

Q =

it{x

x..f

Q = 21,4

rv -

= 14

1,53

ходимо критерії Фішера

між датами F

= ^^ = 1,905

1,05

р _2,00_

та між спостерігачами г

- —— - .

0,60

іівием значущості q% = 5% та ступенями довільності к

- 8, к

- 4 із таблиці

ритерія (див. Додаток, табл.5) для першого випадку маємо F

(D) = 6,04, а

/гого - F

(Q = 19,37 (к

{

=8, к

= 2). Оскільки F

< F

(D) і F

< F

(Q, то

а Н

приймається в обох випадках.

означає, що особисті похибки спостерігачів і різниця дат спостережень не

ають значних систематичних впливів.

§ 3.8. Основи кореляційного аналізу

кне явище природи - це єдність частин і властивостей, які його складають,

ія пізнання явищ необхідно вивчати їх у всій різноманітності взаємовідношень

ючими явищами, а також у взаємозв'язках всіх його сторін. Таке всебічне

зя можна реалізувати, користуючись методами математичної статистики. Але

іняття взаємозв'язків між явищами в математичній статистиці дещо інше, ніж

щознавстві та техніці взагалі. Тут переважно користуються функціональними

остями, коли деяка фізична величина визначається як однозначна функція

їй декількох інших величин.

Елементи математичної статистики

І'Л

Наприклад, теорема синусів в математиці

sin А _ sin В _ sin С

а Ь с

описує залежність між сторонами і кутами трикутника, а закон Ома у фізиці

залежність між силою струму, напругою і опором в електричній мережі. Тобі о,

така залежність існуватиме завжди, якщо існує функція

у =Л*>

•••>

")•

Такий функціональний зв'язок може існувати і між випадковими величинами,

але може існувати залежність іншого роду, яка полягає в тому, що одна з них

величин реагує на зміну іншої зміною свого закону розподілу. Такий зв'язок між

величинами називається стохастичним (ймовірнісним).

Стохастичний зв'язок між двома випадковими величинами проявляється голі,

коли існують загальні випадкові фактори, які впливають на обидві випадкові

величини разом з іншими неоднаковими для обох величин випадковими факто р;

і м и.

Наприклад, деяка величина Хе функцією випадкових величин Z

, ..., Х

F,, ..., F

, a Y- функцією випадкових величин Z,, Z

, ..., Z

, U

, ...,U

f(Z

,...,Z

,...,V

f(Z

,...,Z

,...,U

У такому випадку Xt& Y- стохастично зв'язані, тобто можна говорити про

закон розподілу випадкових величин, які розглядаються; про ймовірності, з якими

зустрічаються ті чи інші комбінації досліджуваних величин.

Головне застосування кореляційного аналізу - в розв'язуванні задач наукового

прогнозу. Його методами можна вказувати межі, в яких

із

наперед заданою надіпі

ііс і

(ймовірністю) буде міститися величина, яка цікавить дослідника, якщо інші, зв'язані

з нею величини, приймають певні числові значення. Наприклад, геодезиста може

цікавити зв'язок між нев'язками в приростах координат кінців сторін триангуляції

(полігонометрії, трилатерації) в залежності від напрямків сторін відносно осей

координат, зв'язки, які виникають при вимірюваннях напрямків та кутів; залежній і.

між виміряними зенітними віддалями і часом спостережень та інше.

Частинним випадком такої залежності є статистична залежність,

коли умовне математичне сподівання однієї випадкової величини є функцією

значень, які приймає інша

M{Y\X=x)=f(x), (3.93)

тобто значення однієї випадкової величини Yв середньому змінюються від

ого,

які значення прийняла інша випадкова величина X. Для оцінки умовного

> Розділ

тичного сподівання необхідно знати аналітичний вигляд закону

ілу системи (X, У). За статистичними даними це зробити неможливо. Як

, в таких випадках можна перейти до оцінок відповідних числових

гристик, у даному випадку до умовного середнього значення

M{Y\X = х) = у(х). (3.94)

а залежність є частинним випадком статистичної залежності і називається

іяційною. Вона характеризується тіснотою і формою.

>актеристикою тісноти кореляційного зв'язку є коефіцієнт кореляції,

гична оцінка його обчислюється за формулою

» K

(3-95)

Ол 0,

1 "

ху

= -х)(у,-у)

П-

1 ;=і

ковий кореляційний момент (вибіркова коваріація);

^J-t-riix,-X)

, So, (3.96)

п -1 /=і

п -1 ,=і

дені оцінки середніх квадратичних відхилень.

овна властивість вибіркового коефіцієнта кореляції полягає в тому, що він

своїх граничних значень -1 та +1 тоді і тільки тоді, коли двовимірний

л (X, У) концентрується на деякій прямій площини (XOY), тобто між Хта Y

>чна лінійна залежність. Якщо

r \ <1, то такої концентрації точок (х, у)

І не буде, якою б тісною не була залежність між Y та X. У тому випадку,

= 0, величини X та Y називаються некорельованими, зокрема,

е завжди, коли Хта Ye незалежними. Однак зворотного висновку зробити

Нерівність г

ху

0 не обов'язково означає, що випадкові величини Хта Y

:жними.

се, за характеристику залежності випадкових величин приймається

звий коефіцієнт кореляції. Якщо ж г Ф 0, то випадкові

m Хта Y називаються корельованими.

ільки вибірковий коефіцієнт кореляції є також випадковою величиною,

ікає питання про надійність його визначення.

ірковий коефіцієнт кореляції приблизно є нормально розподіленим. У

випадку для великих вибірок (обсягом п > 50) використовують оцінку

.ого квадратичного відхилення

Елементи математичної статистики

І'Л

= (3.97)

Гп

Між величинами Хта 7 існує залежність, якщо виконується нерівність

1 -{г )

|г;і>3 (3.9Н)

ЛІП

яка називається критерієм В.І. Романовського.

Зі зменшенням обсягу вибірки (п < 50) зменшується і "нормальність" розподілу

вибіркового коефіцієнта кореляції. У такому випадку оцінку надійності йоі о

виконують методом побудови довірчого інтервалу з використанням функції Фішсра

Z = -(1п(1 + г

ху

) -

1п(1

- г

ху

)), (3.99)

яка підпорядковується нормальному закону розподілу. Величина Z обчислюється

безпосередньо за значеннями вибіркового коефіцієнта кореляції r

або

отримується за цими ж значеннями із відповідно складеної таблиці (див. Додаток,

табл.7). Довірчий інтервал для величини Z буде таким:

- < Z < Z

л]п

-3 ліп-

де Z

- обчислене значення функції Фішера або знайдене за таблицею для

відповідного значення r

-, t - параметр нормального розподілу, який

отримується із таблиці інтеграла ймовірностей для заданої довірчої ймовірнос

і і

(див. Додаток, табл.2).

Після знаходження довірчого інтервалу для функції Z, розв'язавши обернену

задачу, отримаємо довірчий інтервал для коефіцієнта кореляції.

Найважливіші особливості кореляційного зв'язку виражаються в тих змінах, які

зазнає центр умовного розподілу однієї величини за зміною іншої. Геометричне

місі іс

центрів величини У, які відповідають заданим значенням х випадкової величини А",

називають лінією кореляції або регресії Y на X (див. Вираз 3.94).

Аналогічно можна побудувати лінію кореляції або регресії А'на Y

M{X\Y

y) = x(y). (3.100)

Вирази (3.94) та (3.100) і вважають формою кореляційного

зв'язку. Знаходження форми зв'язку - це вже задача р е г р е с і й н о г о

аналізу.

Приклад 17. Нехай г

ху

= 0,75, п = 64. Встановити наявність кореляційног о

зв'язку між величинами А'та У.

> Розділ

скільки п > 50, то для розв'язання задачі використаємо формулу

іановського

І-/

—= 0,0547,

лІП

>о,іб.

з можна стверджувати про наявність лінійного кореляційного зв'язку між

цсовими величинами X та У.

риклад 18. Нехай г

ху

- 0,65, п = 39. Встановити наявність кореляційного

су між випадковими величинами Хта Уіз довірчою ймовірністю у- 0,95.

нашому випадку п < 50, тому для розв'язання задачі використовуємо функцію

ра. За таблицею (див. Додаток, табл.7) знайдемо значення функції Фішера Z

- 0,65

= 0,775.

пя довірчої ймовірності у- 0,95 параметр нормального розподілу t - 1,96.

триманий із таблиць інтеграла ймовірностей (див. Додаток, табл.2). Тоді

чий інтервал для величини Z буде таким:

0,442 <Z< 1,108.

іачення вибіркового коефіцієнта кореляції г

ху

, які відповідають значенням

ції Фішера Z = 0,442 та Z = 1,108, відповідно дорівнюють 0,415 та 0,805 (див.

гок, табл.7). Звідси довірчий інтервал для коефіцієнта кореляції

буде таким:

0,415 <

<0,805.

' ху '

тже, з ймовірністю у- 0,95 встановлюємо, що значення коефіцієнта кореляції

гь в межах від 0,415 до 0,805. Довжина довірчого інтервалу для г дорівнює

- 0,415 = 0,39 і є меншою від самого значення г

ху

Тому можна стверджувати,

іж випадковими величинами Хта Yіснує лінійний кореляційний зв'язок. У

межному випадку, тобто коли довжина довірчого інтервалу є більшою від

:ння вибіркового коефіцієнта кореляції, лінійного кореляційного зв'язку між

яковими величинами Хта Гне існує.

§ 3.9.0снови регресійного аналізу.

3.9.1. Лінійна регресія

рипустимо, що форма функціональної залежності між змінними х та у, відома

ністю до параметрів a

, а

]}

..., а

і має вигляд

Елементи математичної статистики

І'Л

y=f{x, а

, а,,..., а

,). (3.101)

Функція/називається функцією регресії величини Yна X, а співвідношеній!

(3.101) - рівнянням регресії Y на X. Вимагається за результатами спостережені.

(вибірки) (х., у) ,і = 1,2,..., знайти оцінки невідомих параметрів ч

Завданнями регресійного аналізу є:

1) встановлення форми залежності. Як правило, ця форма стає відомою з;і

даними спостережень (див. Рис. 3.15), де точки (х.; у .) - значення вибірок

(вимірювань)

УІ !

о "Т Т ' 0 V

а б в

Рис. 3.15

2) визначення функції регресії (3.100). Процес знаходження функції регресії

називається вирівнюванням окремих значень залежної змінної;

3) оцінка невідомих значень залежної змінної у за оцінками параметрів, що

входять в рівняння регресії.

Розглянемо частковий випадок функцій регресії - лінійні функції^ = а + fix,

які називаються регресійними прямими, або прямими регресії.

Нехай (х, у) - спостережувані (точні) значення, а у = а + fiх, - наближені

значення у

обчислені із рівняння регресії. Тоді величина у

;

-у

є відхиленням

наближеного значення у від точного у (див. Рис. 3.16).

> Розділ

методом найменших квадратів невідомі параметри а і Д прямої регресії

яться із умов мінімізації суми квадратів відхилень, тобто із умов мінімізації

S(a,Д) = Е(Уі-уі)

= ЕСУ,- -а-Дх,.)

і=\ /=1

ирівнявши частинні похідні S

' та до нуля, отримаємо систему

пьних рівнянь

І=І /=І І=І

Рїх

+ап = ТУі-

і=І /=і

зв язавши п, знайдемо

а =

Д =

/=І і=1 і=1 і=1

я , ґ

nlxf- Ех,-

/=1 ^/=1 ,

я я я

і=і і=і /=і

я , (п \

пїх,

- Ех,-

і=1

,=1 j

(3.102)

гко показати, що для значень а та Д, обчислених за формулами (3.102),

іія S(a, Д) набуває мінімуму.

:що необхідно за експериментальними даними отримати лінійне рівняння регре-

і Y, то в рівнянні регресії у - а+Дх потрібно поміняти місцями змінні х та у. При

одержимо рівняння х = d +

/3'у,

де d та Д' обчислюються за формулами

i=}_J=l f=l ,=1

я , f я Л

ПІУ

- ІУі

/= І

ч'-

піу

- їу,

(3.103)