Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань

Подождите немного. Документ загружается.

Елементи математичної статистики

І'Л

Відзначимо, що регресійні прямі у = а + fix

та

х = af + /З'у є різними. Перша

пряма отримується в результаті розв'язання задачі про мінімізацію суми квадратів

відхилень по вертикалі, а друга - при розв'язанні задачі про мінімізацію суми

квадратів відхилень по горизонталі.

На практиці для знаходження рівнянь регресії складається таблиця 3.15.

Таблиця 3.15

Хі

Уі

УІ

ХІУІ

Хі

У1

Л?

' УІ

Х\у\

Х2

У2

У~2

Х2У2

Хп

Уп

УІ

х„у„

І=І

ІЗ*

і= 1

і*

і=1

1=1

і=і

В даній таблиці в останньому рядку суми і визначають коефіцієнти «та /Забо

а'та /З'за формулами (3.102) або (3.103) відповідно.

Рівняння лінійної регресії можна побудувати, використовуючи вибірковий

коефіцієнт кореляції

У -

= г

у/х

•

(х - х) - рівняння прямої регресії

на X,

х - х = г

х/у

(у-у) - рівняння прямої регресії X на Y,

де х,у - середні вибіркові; г

хІу

, г

уІх

- коефіцієнти лінійної регресії; S

, S

виправлені середні квадратичні відхилення вибірок;

- ,*

o* *

і і

— Г

—

xi У

ХУ

'у/х ~

'ху

Прямі регресії проходять через точку (Зс;^). Вони збігаються, якщо | г* |

= 1.

Вибірковий коефіцієнт кореляції r

= ±^jr

y/x

•

xjy

Є середнім геометричним

коефіцієнтів лінійної регресії.

Приклад 19. За даними таблиці спостережень

X,- 2

УІ

скласти рівняння регресії Y на X та X на Y.

> Розділ

адемо таблицю 3.16.

Таблиця 3.16

У:

УІ

ХІУІ

2 5 4 25 10

4 3 16

9 12

6 7 36

49 42

Іх, = 12

Ь,= 15

/=1

ixf = 56

і=|

= 83

;=і

І = 64

формулами (3.102) для п = 3 отримуємо

56-15-12-64 „ . 3-64-12-15 1

а- г— = 3; р= — =

—.

3-56-12

-56 -12 2

ке, рівняння регресії Y на X буде

в х =

3 +

—.

шогічно за формулами (3.103) знаходимо:

, 83-12-15-64 3 3-64-15-12 1

а = г— = -; р =

г—

= -.

3-83-15 2 3-83-15 2

Елементи математичної статистики

І'Л

Звідси рівняння X на Y буде

а'+ Вх

—.

2 2

1 13

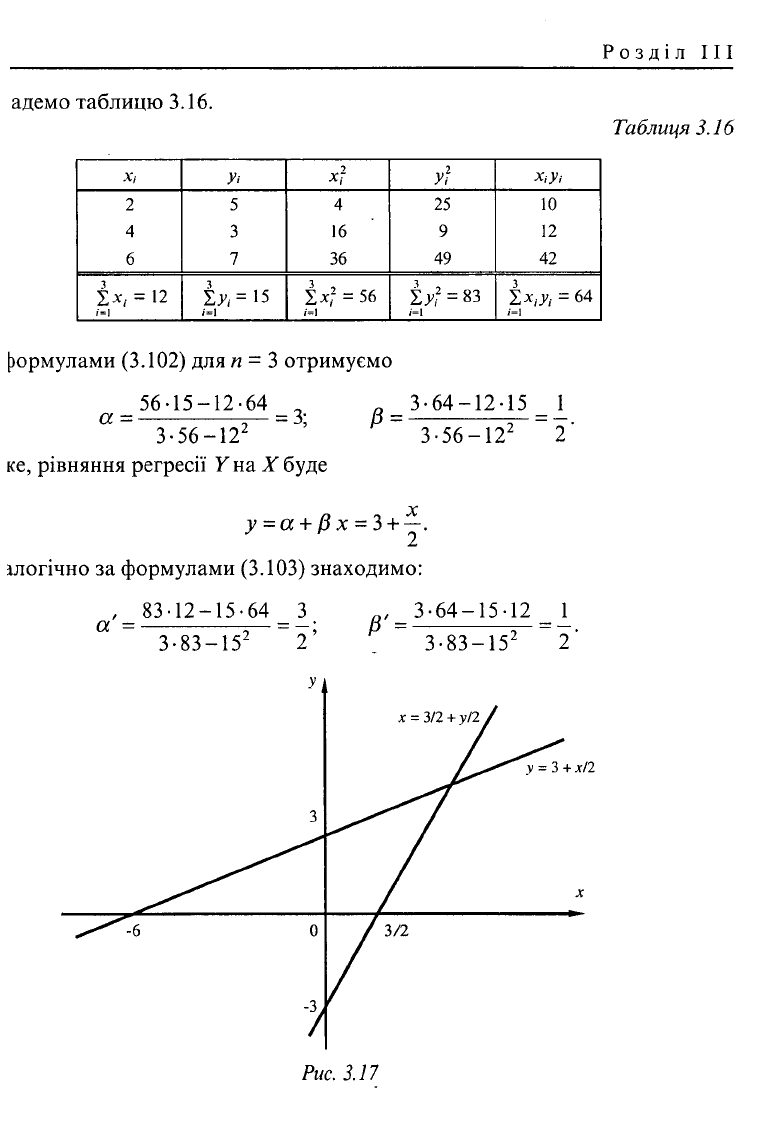
Із отриманих рівнянь видно, що регресіині прямі У~— х + 3 та х =

— У

+ ^ '

дійсно різними. Побудуємо їх (див. Рис. 3.17).

3.9.2. Нелінійна регресія

Рівняння регресії (3.101) може описувати різні лінії (не тільки прямі).

Наприклад, нехай воно набуває якогось із таких виглядів:

а) у = а

+ а

{

х + а

;

а,

б)

= а

+ -L;

в) у =

+ а

{

х + а

+ ах

г)y = a

+ a

logx;

д) у

а? .

Невідомі параметри (коефіцієнти) цих рівнянь знаходяться також за методом

найменших квадратів.

Наприклад, для параболічної кривої у = а

+ а^х + а

коефіцієнти а

{)

, а

знаходимо зі системи рівнянь

Zxf +а^Хі+п-а

=ХУі

і і і

• thZxf +a

Y,xf +а

2х, =1x

(3.104)

і і і

£ х,

+ а,

S xf

£ х

І а)у,.

і і і

Якщо рівняння регресії такого вигляду:

у = а

+ а,х, + а

+ ... + ах

, (3.105)

то така регресія називається множинною регресією. Тоді вектор оцінок

коефіцієнтів а = (а

, а

, ..., aj визначається в матричній формі

b = (X

X)-

Y). (3.106)

> Розділ

гтя задача регресійного аналізу означає прогнозування значень

жуваної змінної у, яка в статистиці носить назву відгуку на відомі значення

;трів х.(і =1,2,...), які в свою чергу називаються регресорами. Вони можуть

атися дослідником (тоді маємо першу модель регресійного аналізу), або

затися довільно і випадково незалежно від дослідника (друга модель

ійного аналізу). Методика обчислень за 1-ою та 2-ою моделями є

>вою, тільки змінюється інтерпретація результатів в умовах кожної моделі.

РОЗДІЛ IV

ЕЛЕМЕНТИ ТЕОРІЇ ПОХИБОК

ВИМІРЮВАНЬ

§ 4.1. Предмет і задачі теорії похибок вимірювань

Будь-які геодезичні роботи пов'язані з вимірюваннями, які отримуються

завжди з деякими похибками. На результати вимірюваної величини впливаю

точність вимірювального приладу, метод вимірювання, кваліфікація спостері га ч а,

зовнішні умови та ін. Точність результату вимірювання залежить від названих та

інших випадкових і систематично діючих факторів, які при переході від одного

вимірювання до іншого змінюються та обумовлюють його випадкові коливання

або систематичні відхилення відносно деякого середнього значення шуканої

величини.

Похибки вимірювань, обумовлені вище наведеними факторами, а саме

недосконалістю приладів та методів вимірювання, обмеженою чутливістю органів

чуття спостерігача, несприятливими зовнішніми умовами тощо, обов'язково і

неминучими. Вказані фактори, що викликають появу похибок, впливають незалежі

к >

один від одного і тому остаточне значення похибки буде як результат сумарного

ефекту впливу всіх джерел похибок, що мають місце в процесі вимірювання. Таким

чином, теорія похибок вимірювань розв'язує такі основні задачі:

1) встановлення законів розподілу похибок вимірювань;

2) визначення на основі результатів вимірювань найбільш надійних значень

шуканих величин;

3) виконання оцінки точності отриманих значень шуканих величин;

4) визначення допусків, тобто граничних значень похибок;

5) встановлення законів накопичення похибок як у процесі вимірювань, так і

при опрацюванні їх. -

§ 4.2. Вимірювання та їх класифікація

Вимірювання - це встановлення відношення величини, що вимірюється, до

іншої однорідної величини, яку прийнято за одиницю міри, тобто

> Розділ IV

вимірювана величина; N- одиниця міри; L - числове значення величини М.

мірювання поділяють на:

Прямі (безпосередні) та непрямі (посередні) за фізичним виконанням

рігача. Якщо вимірювану величину' можна безпосередньо порівняти з

дею міри, то це є пряме вимірювання. Довжина лінії, виміряна за допомогою

овальної стрічки, величина кута, який виміряно за допомогою теодоліта,

іна перевищення, виміряного за допомогою нівеліра та рейки - це є прямі

овання.

:е

часто буває так, що потрібно знати значення величини, яку безпосередньо

іти неможливо. У цьому випадку застосовують непрямі вимірювання, за

огою яких отримують значення величин, через які функціонально

ається інша величина, яку неможливо безпосередньо виміряти.

іглянємо для прикладу рівносторонній трикутник. Потрібно виміряти радіуси

юго та описаного кола. Зрозуміло, що дані вимірювання будуть непрямими,

іезпосередньо за допомогою вимірювальної стрічки можна виміряти сторону

ника (див. Рис. 4.1), а потім визначити шукані радіуси, оскільки вони є

іонально пов'язані зі стороною трикутника а такими співвідношеннями:

aS „ «л/З

Рівноточні та нерівноточні за точністю, яка обумовлюється умовами

звань. Рівноточні вимірювання однієї або декількох однорідних величин -

езультати вимірювань, які отримано при однакових умовах, а саме одним

ке методом, спостерігачами однакової кваліфікації, приладами однакової

;ті вимірювання, при однакових приблизно зовнішніх умовах тощо.

Елементи теорії похибок вимірювань

239

Якщо вимірювання однієї або декількох однорідних величин проведено при

неоднакових умовах, то вони є нерівноточними.

Розглянемо, наприклад, ряди широтних спостережень за яскравою зені тною

зіркою a Persej, які проведено весною та восени. Зрозуміло що ці вимірювання г

нерівноточними, оскільки їх виконано при різних зовнішніх умовах.

3). Необхідні та додаткові за кількістю. Вимірювання, які проведено для

отримання хоча б однієї системи значень шуканих величин, називаючися

необхідними. Якщо з тією ж метою крім необхідних вимірювань виконані ще

якісь вимірювання, то вони називаються додатковими або надлишковими.

Розглянемо довільний трикутник на площині, в якому потрібно знати значення

кутів. Достатньо виміряти два кути, наприклад

се

та/З (див. Рис 4.2), а третій куч у

знайти зі співвідношення у=

180°

- а - Д Якщо виміряти і кут у то дане вимірюва п н я

буде надлишковим. Проведення надлишкових вимірювань є обов'язковим. Вони

дозволяють виявити грубі похибки, знайти надійні значення виміряних величин

підвищити точність результату вимірювань.

4). Залежні та незалежні за умовами вимірювань. Залежними називаються

ч а к і

вимірювання якоїсь величини, які впливають на результат вимірювання іншої

величини. У протилежному випадку вимірювання називаються незалежними.

Наприклад, вимірявши кути а,

та у у трикутнику (див. Рис. 4.2), можна знай

їх суму S - а + /З + у. Вимірювання кутів можна здійснити незалежно один під

одного. Але якщо розглядати суму S з кожним із кутів а, Д уто, наприклад S і с

є залежними, оскільки похибка, допущена при вимірюванні кута а впливатиме

на результат суми кутів S. Залежними також будуть вимірювання S і

та S і у.

§ 4.3. Похибки вимірювань і поправки до їх результату

У процесі вимірювання крім об'єкта вимірювання, приймають участь прилади,

спостерігачі, які використовують ці прилади, а також і, звичайно, на резульч

ач

впливає зовнішнє середовище. Весь цей комплекс умов може змінюватись і

> Розділ IV

/вати точно ці зміни неможливо. Тому в результаті вимірювання отримані

:ння будуть відрізнятися від істинних.

ззглянемо істинне значення L вимірюваної величини та її виміряні значення

і =

п). Тоді величини

A=l-L (4.1)

заються істинними похибками вимірювань /.. Дані похибки виникають через

сконалість приладів вимірювання, обмежену чутливість органів чуття

^ерігача, несприятливі зовнішні умови тощо.

скільки цілком усунути істинні похибки неможливо, то вводяться поправки

гзультатів вимірювань І. так, щоб досягнути найменших значень А.. У

ьному випадку, але цього досягти дуже важко, поправки можна визначити

зом v. = L - /. і тоді істинні похибки А. будуть рівними нулеві.

§ 4.4. Класифікація похибок вимірювань

а своїм походженням у результаті вимірювань, похибки поділяються на

іументальні, особисті та зовнішнього середовища, а за характером впливу

:зультати вимірювань і за своїми властивостями - на систематичні, грубі та

дкові.

тструментальні похибки обумовлені недосконалістю виготовлення, не цілком

ою перевіркою (юстировкою) та встановленням в робочий стан для

гережень, а також зміною властивостей вимірювального приладу з бігом часу,

похибки можуть бути частково усунені спостерігачем у процесі вимірювання,

(собисті похибки вимірювань виникають у результаті обмеженої чутливості

нів чуття, недостатньої кваліфікації, досвідченості та психологічного стану

герігача.

Іохибки зовнішнього середовища, викликані несприятливими зовнішніми

орами та умовами вимірювань. Це температура, атмосферний тиск, вологість,

іозорість повітря, вітер, рельєф місцевості, нестійкість ґрунту тощо. Для

ування або послаблення таких похибок доводиться вводити поправки,

иклад, за атмосферним тиском або за температурою. Також вживають спеціальні

ци для проведення вимірювань у сприятливіших умовах, або застосовують

іальні методи спостережень. Цілком усунути такі похибки неможливо.

Систематичні похибки - це такі похибки, які появляються в результатах

рювань за певним законом в залежності від факторів, що обумовлюють їх

ікнення. Дані похибки є сталими та змінними.

Сталими систематичними похибками називаються похибки, обумовлені

ійно та незмінно діючими факторами, які в процесі вимірювання не змінюються

Елементи теорії похибок вимірювань

241

за абсолютною величиною. Вони виникають внаслідок недосконалості

виготовлення, не точної перевірки та приведення в робочий стан приладу

вимірювання, незмінної дії під час вимірювань факторів зовнішнього середовища

та багатьох інших причин. Щоб виявити сталу систематичну похибку, слід провсс

і п

спеціальні дослідження або вимірювання, у результаті яких буде отримано її числове

значення.

Змінними систематичними похибками називаються похибки, які у процесі

вимірювання довільної величини змінюють своє значення за абсолютною

величиною та аналітична форма закону зміни залежить від характеру впливу на

результати вимірювань факторів, що їх викликають.

Грубі похибки (промахи) - це такі похибки, які неможливо допустити при даних

умовах вимірювань. Вони виникають головним чином через неуважність і

недбайливість спостерігача. Щоб виявити їх слід проводити контрольні та повторі і і

вимірювання. Грубі похибки повинні бути усунені з результатів вимірювань.

Випадковими похибками називаються такі похибки, абсолютне значення яких

у процесі вимірювання довільної величини змінюється без всякої закономірності.

Випадкова похибка є сумою елементарних похибок, обумовлених впливом

багатьох відомих і невідомих нам факторів. Поява даних похибок у результатах

вимірювань є неминучою, усунути їх неможливо хіба що за допомогою сучасних

вдосконалених методів вимірювань, достатньо точних приладів, вибравши

найбільш сприятливі зовнішні умови, абсолютні значення їх звести до певного

мінімуму.

Слід відзначити, що інструментальні похибки носять переважно систематичний

характер, а особисті похибки та похибки зовнішнього середовища - випадковий.

Наведемо властивості випадкових похибок:

1) при даних умовах вимірювань випадкові похибки за абсолютною величиною

залишаються завжди меншими за якесь граничне значення;

частота малих за абсолютною величиною похибок є більшою за частоту великих;

3) частоти додатних і від'ємних похибок є завжди однаковими;

4) границя середнього арифметичного значення випадкових похибок є рівною

нулеві при необмеженому зростанні їх кількості;

5) у ряді випадкових похибок при переході від однієї похибки до іншої не

проявляється ніякої закономірності щодо її абсолютної величини.

§ 4.5. Критерії для оцінки точності результатів вимірювань

Задача знаходження найбільш надійних значень виміряних величин спонукає

до розв'язування іншої задачі, а саме до встановлення оцінки точності результатів

вимірювань.

> Розділ IV

Зчевидно, що на основі одного вимірювання про точність отриманого

льтату судити не можна. Але якщо буде відома велика кількість результатів

ірювань деякої величини та істинні похибки, то, проаналізувавши їх, можна

инути грубі, а в деяких випадках і систематичні похибки. Після цього можна

тмати ряд випадкових істинних похибок.

Якщо розглядати декілька рядів випадкових істинних похибок, то судити про

зість результатів вимірювань необхідно за їх мірою розсіювання, тобто чим

ше вони відрізняються між собою, тим є точнішими і навпаки, чим більше

и відрізняються один від одного, тим менш точними слід їх вважати.

Для оцінки точності результатів вимірювань прийнято такі критерії: середня

ибка, ймовірна похибка та середня квадратична похибка.

Середньою похибкою в називається середнє арифметичне з абсолютних

гень істинних похибок А

(і = \,п) результатів вимірювань

п п

Розглянемо довільний ряд випадкових похибок результатів вимірювань деякої

ичини.

Абсолютним варіаційним рядом випадкових похибок називається послідовність

их похибок, розміщених в порядку зростання або спадання за їх абсолютною

ичиною.

Ймовірною похибкою р називається таке значення абсолютного варіаційного

у випадкових похибок, яке ділить даний ряд на дві рівні за обсягом частини.

Розглянемо такий ряд випадкових похибок:

-0,01; 0,12; 0,56; -0,35; 0,06; -0,11; -0,05; -0,20; -0,08; 0,09; -0,19; -0,18; 0,32; -0,45;

); -0,44; -0,57.

Побудуємо абсолютний варіаційний ряд

0,01; 0,05; 0,06; 0,08; 0,09; 0,11; 0,12; 0,18; 0,19; 0,20; 0,30; 0,32;0,35; 0,44; 0,45;

3; 0,57.

Посередині даного ряду знаходиться значення 0,19. Тому ймовірна похибка

0,19.

У наведеному прикладі обсяг N вихідного ряду похибок дорівнював непарному

;лу 17. Якщо обсяг N вихідного ряду похибок дорівнюватиме парному числу,

ймовірною похибкою буде середнє арифметичне двох значень абсолютного

>іаційного ряду, які потрапляють на середину.

Середньою квадратичною похибкою т називається величина, яка

зівнює квадратному кореню зі середнього арифметичного квадратів

инних похибок