Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань
Подождите немного. Документ загружается.


Елементи лінійної алгебри З І
Так само можна перевірити, що і
А~
1
=-
1
det(^)
А*А-Е. Отже, ми довели, п
det(^t)
Очевидно, що для заданої матриці А її обернена матриця А'
1
буде єдиної
Дійсно, якщо крім А'
1
існує ще одна обернена матриця В, тобто якщо А В = Е, то
А 'АВ = А 'Е, звідки випливає, що В = А'
1
. Аналогічно, якщо СА = Е, тоді С = А
що й доводить єдиність оберненої матриці.
Зауваження. Особлива квадратна матриця оберненої не має. Дійсно, які,
det(/4) = 0, то з рівності det(AA~') = det(A)det(A~') = det(£) = 1 випливає, рівпісі
0=1, що неможливо.
Таким чином, ми встановили факт, що обернену матрицю має тільї
квадратна неособлива матриця.
Приклад. Для матриці А
••
Ґ
1 2 З
л
2 4 5
3 5 6
v
знайти обернену.
Розв'язання. Оскільки визначник det(^)=
1 2 З
2 4 5
3 5 6
= -1^0, то матриця А
неособливою.
Обчисливши алгебраїчні доповнення елементів матриці А, складемо союч
матрицю
Г-1 З -2
N
А*= З -З 1
-2 1 0
V у
Поділивши всі елементи цієї матриці на det(^) = -1, одержимо оберне
матрицю до матриці А, тобто
' 1 -З 2
Л
А''= -З З -1
2-10
V ;
Наведемо деякі основні властивості оберненої матриці, які легко перевіри
l)deL4-' =
1
det (А)'

12 Розділ I
2) (А В) ' = В 'А '-
3) (А"')
т
= (А
т
)
_1
.
1.1.5. Клітинні матриці
Розглянемо деяку матрицю А. Розіб'ємо її на матриці нижчих порядків (клітини
і блоки) за допомогою горизонтальних та вертикальних ліній, що йдуть через
) матрицю. Наприклад,
А =
12
22
32
13
23
•*33
(Р
R
V
Q
s
клітинами є матриці Р =
42
22
, Q =
\
'13
23
v
z
-v
Я = («зі а
і2
), 5 = (азз).
Матриця, яка розбита на клітини, називається клітинною. її елементами
'жать матриці-клітини. Зрозуміло, що розбиття матриці на клітини може бути
йснено різними способами. Зокрема, частковим випадком клітинних матриць
вазідіагональні матриці
клітини А.(і = 1,2,...,/с) є квадратними матрицями можливо різних порядків, а
за клітинами стоять нулі.
Очевидно, що det(^) = det(v4
/
)det(^
2
)...det(^
(t
). Іншим важливим частковим
падком клітинних матриць є обведені матриці
Л-І =
21
12
22
л-12
А. =
Чи-1
2л-І
п—\п—]
и.
V.
п-1
*2л
•
число. Наприклад, матрицю
к
а
п-\пJ
-(
а
пІ>
а
»2>-">
а
л,п-і)
>

Елементи лінійної алгебри
З І
Ґ
3 10 2
-3 4 5 7
12 3 4
-5 3 0 1
можна записати у вигляді обведеної матриці
V
4 =
V
F
3 «44
у
( 3
1
F
2
"
де /і
3
=
-3
4 5
. ^3 =
7
1
ч
2
3
У
4
V /
, F
3
-(-5 3 0) а
44
= 1.
Клітинні матриці зручні тим, що дії над ними проводяться формально за тим
ж правилами, як і над звичайними матрицями.
Дійсно, нехай клітинні матриці
А =
А
И
А
п
А
р і А
р2
••• А
рч
і В =
ґ
В
п
5
І2
В
г\
В
г2
В
В.
є матрицями однакового типу і з однаковим розбиттям, тобтор - r, q = s і клітин
А у та В z одного типу.
Тоді легко зрозуміти, що
А + В-
А
и
+
В
и
А
п
+5
12
Л
р2
+В
р2
А
РЧ
+ В
РЧ
І'очглянемо задачу множення клітинних матриць. Припустимо, що матриці
і Н с попередньої структури, причому q = г і, крім цього, припустимо, що I
і
клітини А та В.
к
(і= 1, 2, ...,p-,j= 1, 2, ..., q\ к = 1, 2, ..., 5) є такими, що кількіс
стовпчиків клітини
А
„дорівнює кількості рядків клітини B
jk
. Тоді можна ДОНСС'І
що добуток АВ є клітинною матрицею
С =
11 12
с
2і
с
22
С
р\
С
р2
ь
2 І
ps

14
Розділ I
де С
ц
= АцВ
1к
+ А
п
В
1к
+...
+
A
iq
B
qk
(і = 1,2, ...,р; к = 1,2, ...,s), тобто матриці А та В
перемножується так, ніби на місці клітин знаходяться числа.
Приклад.
. Знайти АВ.
Розіб'ємо матриці А і В на клітини, позначивши через Р-(3 1), Q-(2),
Г
=
( 4),Х
=
(2 1).
г 3
1
2
1
(1 2
3
1
А =
4 -1 1
, в =
3 -2
1
5
V
3
2
У
4
V
2 1
У
f 4
-г
'П
гп
Ґ
2
R =
, 5 = , и = , v
=
5 3 2 3
-2 1
V У V У V У Ч У
Тоді
А =
(Р Q
R S
Отже, А В =
ґ
PU+QT PV+QX
Л
RU
+
ST RV+SX
В =
Т
\
V
N
JSf
У
14 8
12
1
5
10 12
22
8
20
Особливо просто здійснюються додавання та множення квазідіагональних
матриць. Дійсно, якщо
А =
, в =
5,
В С
і матриці А. та В.(і = 1,2,..., s) є одного порядку, то в результаті додавання та
множення їх маємо
А
+
В =
А
х
+В
х
A
s
+
B
s
'А
х
-В
х
і АВ =
1.1.6. Обертання матриць за допомогою розбиття на клітини
Знайдемо обернену матрицю Адля квадратної неособливої матриці А п-го
порядку. Для цього розіб'ємо матрицю А на чотири клітини

Елементи лінійної алгебри З І
a
2l
(s,r)
а
22
0,.ї)
Тут в дужках вказано порядки відповідних клітин, причому r + s = п
шукати обернену матрицю А'
1
також у вигляді чотириклітинної матр
А~
1
=
а
п
(г,г)
a
2l
(s,r)
a
l2
(r,s)
a
22
(s,s)
Оскільки А -А = Е , то, перемноживши ці матриці, одержим
матричні рівняння для визначення матриць ~
1>
2)
Рп<*п
Ріі
а
і2
Ми
Р
21
ос
12
+ 3
12
а
21
+ Рі
2
С*22
+ 3
22
С^
2
і
+ Р
22
сх
22
О
О
F
де Е та Е„- одиничні матриці г-го та s-ro порядку, відповідно. Ро
Г
• —1
систему (1.6), визначимо клітини матриці А . Для цього помножі
частину першого рівняння системи (1.6) на сс^
]
сс
п
та віднімемо від ні
рівняння цієї системи. В результаті отримаємо, що
Р\2 СС
22
)—(Х
п
СС
12 •
звідки
Р\2 ~ ^11^12(^22
®21®11®12^
-1
011 =«П ~Рі2
а
2і
а
Аналогічно із третього та четвертого рівнянь системи (1.6) знайде
Р22
=
(&22
~ ^21^11^12) >
^21 ~ /^22^21^11 '
Таким чином ми отримали всі клітини оберненої матриці. Для пр
застосування вказаного методу введемо такі матриці:
X
— 01ц
-а
х2
, Y
=
ct
2i
-a
u
,
Тоді формули для клітин Pij(i,j = 1,2) можна записати простіше

16 Розділ I
)8„ =«,-/+ЛГв-'У,•
р
п
=-хв~
1
,
шуставши, що aj"/ та 0~' існують. У результаті обернена матриця буде мати
•ляд
'a;l+X0-
l
Y
-0
Ч
У 0-
1
Приклад. Обернути матрицю
А =
1 0 3
-4
0
1
5
6
-3
4
0
2
-5 -6
2 0
Покладемо
'1
«П
—
0
1
?
У
/
3
4 ^
«21
=
5 -6
V У
у
ґ
3 -4
Л
5 6
V
а
•22
'0
2 0,
v у
Тоді
^С —
Ої
j j
Ої j 2
—
(\
°1
-1
ГЗ
~
4
)
ГЗ
0
V
1
У
5
V
6
У
5 6
V У
У^ —
і^і і
— 1 —
/
-3 4
Л
-5 -6
0 -а
22
-а
2Х
Х -
Тому
011 =
ґ
0
2 0,
v у v
•З 4
-5 -6
З -4
5 6
-11 -34
47 16
'1 0") ГЗ -4V-11 -34
0 1
+
5 6
v У V у v
47 16
У Г-3
4 ї
і г
У
-5
\
-6
У
1422
-16 68
N
86 -10 '
У
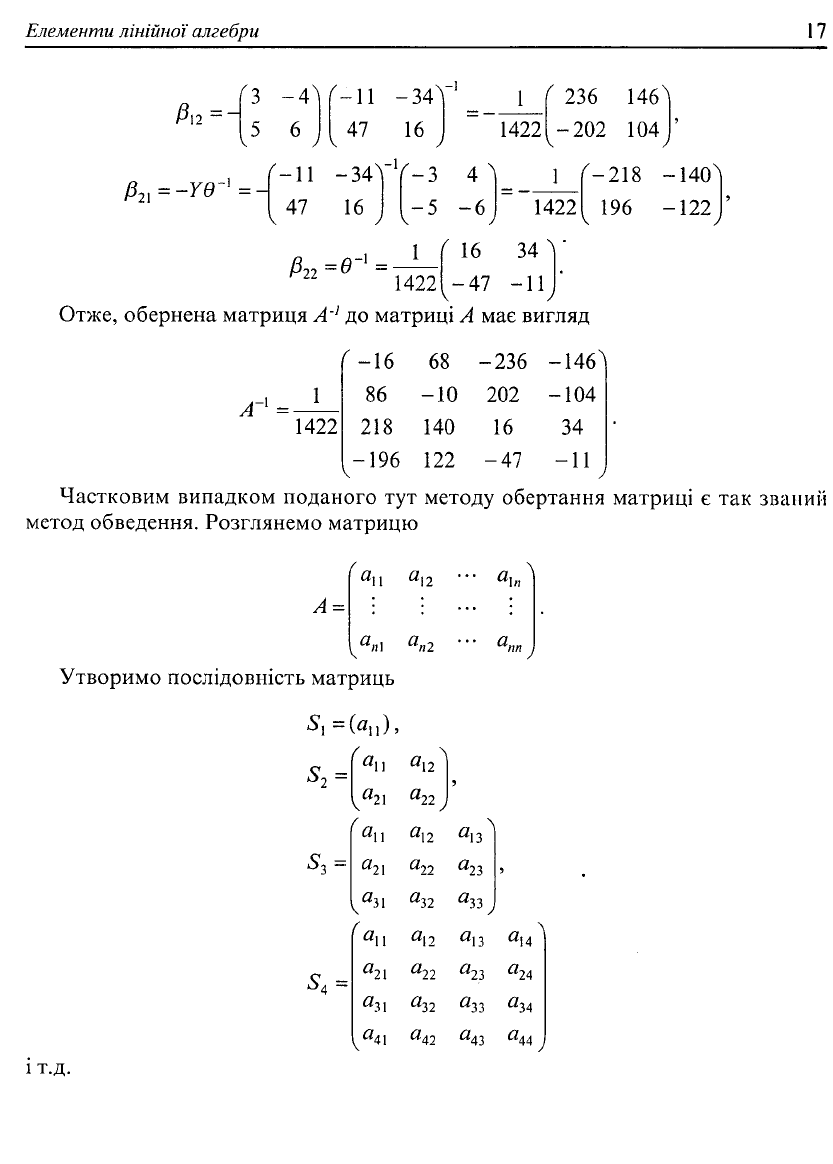
Елементи лінійної алгебри
З І
/3.2="
З -4
5 6
л
' -11 -34
4
"'
47 16
Ґ
236 146
л
1422
1-і
'21
f-11
-і
Г-3 4 ^
1
47
V
16
У
-5 -6
V У
1422
V
-202 104
'—218
196
Р
22
=в~
1
=
1422
16 34
-47 -11
Отже, обернена матриця А'
1
до матриці А має вигляд
А~
1
=-
1422
-16 68
86 -10
218 140
-236
202
16
-146
4
-104
34
-196 122 -47 -11
J
у
140
•122
Частковим випадком поданого тут методу обертання матриці є так званий
метод обведення. Розглянемо матрицю
А =
Утворимо послідовність матриць
S
2
=
12
п2
(«її),
ґ
а
и
«12 "
,«21 «22,
)
ґ
а
и
«12
«із
4
«21 «22
«23
5
,«31 «32
«33 ,
/
«н «12
«13 «14
«21 «22
«23 «24
«31 «32
«33 «34
«41
«42
«43 «44
1 Т.Д.

18 Розділ I
Обернена матриця 5,'
1
до матриці S
2
знаходиться безпосередньо. Маючи S
2
'\
зснові методу обертання клітинних матриць, можна знайти S^
1
і т. д., поки не
йдемо S
n
= А"
1
.
Зауважимо, що метод обведення матриці є непридатним, якщо одна із
>міжних матриць S. є особливою.
1.1.7. Ранг матриці
Розглянемо прямокутну матрицю
А =
<21
ш 1
12
22
ті
1
\п
*2п
імірності тхп. Нехай число к < т і к<п . Виділимо в цій матриці які-небудь к
(ків і к стовпчиків. Із елементів, які стоять на перетині виділених рядків та
•впчиків, складемо визначник А>го порядку. Такий визначник називається
;ором к-го порядку матриці А. Зрозуміло, що з матриці розмірності тхп можна
асти мінорів к-го порядку.
Наприклад, з матриці
А =
V
3 2 4 2'
2 0 11
0 4 5 1
розмірності 3x4
жна скласти С\С\ =12 мінорів першого порядку - це самі елементи матриці,
Cj =6x3 = 18 мінорів другого порядку
3 2 3 4 3 2 2 4 2 2
4 2
3 2 3 4 3 2
2 0
?
2 1
>
2 1
>
0 1
9
0 1
>
1 1'
0 4
5
0 5
)
0 1
2 4 2 2 4 2 2 0 2 1 2 1 0 1 0 1
4 5
і
4 1 '
5 1
5
0 4
5
0 5
І
0 1
>
4 5
)
4 1
9
С
4
С
3
=4 мінорів третього порядку
3 2 4 3 2 2
2 0 1,2 0 1
0 4 5 0 4 1
4 2
0 1
5 1
2 4
0 1
4 5

Елементи лінійної алгебри
З І
Рангом матриці називається найвищий порядок мінору, відмінного від нуля.
Таким чином, якщо ранг матриці дорівнює г, то це означає, що серед мінорів цієї
матриці знайдеться хоча б один мінор
/--го
порядку, який не дорівнює нулеві, а всі мінори
порядку вищого ніж г, дорівнюють нулеві. Ранг матриці А позначають символом г(А).
Легко перевірити, що в наведеному прикладі всі чотири мінори третього
порядку дорівнюють нулеві, а не всі мінори другого порядку дорівнюють нулеві.
І
Іе й означає, що ранг цієї матриці дорівнює двом, тобто
г(А) = 2.
Для знаходження рангу матриці корисно спочатку звести її до більш прос того
вигляду за допомогою так званих елементарних перетворень.
Елементарними перетвореннями матриці називаються такі дії над елементами
матриці:
1. Перестановка місцями двох рядків або стовпчиків.
2. Транспонування матриці.
3. Множення всіх елементів рядка або стовпчика на деяке відмінне від нуля число.
4. Додавання до всіх елементів рядка (або стовпчика) відповідних елементін
іншого рядка (або стовпчика), помножених на одне й те ж число.
Дві матриці називаються еквівалентними, якщо одна з них отримана з іншої
за допомогою скінченого числа елементарних перетворень. Зрозуміло, що такі
матриці не рівні між собою, але їхні ранги рівні, про що стверджується в теоремі.
Теорема. При елементарних перетвореннях матриці їїранг не змінюється.
Доведення теореми безпосередньо випливає із властивостей визначників.
Приклад. Знайти ранг матриці
3 2 12
А= 2 0-1 1
0 4 5 1
V ,
Розв'язання. Перший рядок помножимо на 2 і віднімемо його від третього:
г(А)
=
г
З 2
2 0
-6 0
1 2
л
1
-З
Поділимо другий стовпчик на 2, а потім віднімемо від першого стовпчика
потроєний другий, від третього - другий, від четвертого - подвоєний другіїіі.
І
Іісля цього одержимо:

20 Розділ I
Г(А):
З
2
1
0
0
З
о
2
-6
1 0
0 -1
о з
0 ^
1
-з
Го
1 0 Го 1 0
°1
Го 1 0
г{А)
=
г 2 0 -1 1
= г і
0
-1 1
—
г і 0 0 0
0
V
0 0 0
0
V
0 0 0 0
V
0 0 0
У
ізніше додамо до третього рядка потроєний другий. Поділивши потім
ий стовпчик на 2, додамо його до третього стовпчика. І, нарешті, віднявши
від четвертого, отримаємо, що
= 2.
1.1.8. Норма матриці
багатьох випадках є корисним мати можливість приписати матриці деяке
значно визначене невід'ємне число для оцінки міри її величини, як, наприклад,
іектора такою оцінкою є його довжина. Для матриці за міру її величини
мають норму.
Нормою матриці А називається дійсне число || А ||, яке задовольняє такі умови:
)
II
А
II
> 0, причому IIАII = 0 тоді і тільки тоді, коли А = О;
)
II
А а
II =|
а
ІУ
А || (а - число); зокрема ||-А
||
= \\А ||;
) ІМ +
.В II
-ІМ
II
+
II
II;
ИМД||<|М||Х||2?||.
кщо крім цих чотирьох аксіом норма задовольняє ще умови
) А = (а
ц
),
І
а
и
І
< |М II;
)
із нерівності
І
А
І
< ІВІ випливає нерівність || А
|| < ||
В ||, зокрема \\А || = ||| А |||,
ка норма називається канонічною. Тут \А | = (| a
tj
|).
!
декілька норм матриці. Часто зустрічаються такі:
. || А ||
m
= шах 11 а
у
\ (
т
.норма);
j
А 11/= max XI а у \ (/-норма);
\^\\
к
=Ша
{і
\ (/с-норма).
І
'•/
