Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань

Подождите немного. Документ загружается.

Елементи математичної статистики І'Л

дослідженнях. Довірчий інтервал визначає межі (кінці інтервалу), між якими м

у= (1 - «)% експериментів знаходиться істинне значення оцінюваного парамс

ра

3.6.5. Перевірка гіпотези про рівність дисперсій двох нормально

розподілених генеральних сукупностей

Перевірка таких гіпотез в геодезичній практиці пов'язана з порівнянням

характеристик точності геодезичних інструментів та різних методів спостережеш.

Очевидно, що кращим буде той метод чи інструмент, який забезпечує найменше

розсіювання результатів вимірювань.

Розглянемо гіпотезу про рівність дисперсій двох нормально розподілених

генеральних сукупностей. Для перевірки такої гіпотези необхідно знати іаку

функцію їх статистичних оцінок, розподіл якої не залежав би від будь-яких

невідомих параметрів. Такій умові задовольняє розподіл відношення двох

незміщених оцінок дисперсій, отриманих із незалежних вибірок

^02

Вираз (3.66) використовують у випадку, коли математичні сподівання вибірок

є невідомими. Якщо математичні сподівання вважаються відомими, годі

використовують зміщені оцінки дисперсій

У більшості практичних випадків використовують вираз (3.66) і вибираюп.

його так, щоб у чисельнику знаходилось число більше, ніж у знаменнику. Величина

і^має F-розподіл (Фішера-Снедекора). Цей розподіл, як відомо, залежить тільки

від кількості ступенів довільності к

= п

і к

= п

- 1 (и , п

- обсяги вибірок, із

яких знайдено оцінки першої і другої дисперсій відповідно).

Сформулюємо гіпотезу про рівність дисперсій двох нормально розподілених

генеральних сукупностей.

Нехай сукупності Хі F розподілені нормально. За незалежними вибірками з

обсягами п

і п

, відібраними з цих сукупностей, знайдено виправлені вибіркові

дисперсії 5

0д

. і S

. Необхідно за виправленими дисперсіями та за вибраним

рівнем значущості А перевірити нульову гіпотезу Я

: D(X) = D( Y). Через те, що

виправлені вибіркові дисперсії є незміщеними оцінками, нульову гіпотезу можна

записати так:

: M[ST-J = M[ST-J.

> Розділ

<а задача ставиться тому, що, як правило, вибіркові дисперсії є різними,

иникає запитання, чи суттєво відрізняються між собою вибіркові дисперсії,

що станеться так, що нульова гіпотеза справедлива (генеральні дисперсії є

звими), тоді різниця між виправленими дисперсіями є незначною, що

зється випадковими причинами (наприклад, випадковим відбором об'єктів

и). Припустимо, що різниця виправлених вибіркових дисперсій результатів

звань, виконаних двома різними методиками, виявилася незначною. Це

є, що методики забезпечують однакову точність результатів,

що нульова гіпотеза буде відхилена (генеральні дисперсії є різними), тоді і

ія між вибірковими дисперсіями є значною (суттєвою) і не може

оватися випадковими причинами, а є наслідком того, що генеральні

•сії в дійсності є різними. Це значить, що точність застосованих методик

треба вибрати точнішу.

ревірка гіпотези про дисперсії виконується за тим самим порядком, який

влений для перевірки раніше розглянутих гіпотез.

ітистичним критерієм перевірки гіпотези про рівність дисперсій двох

пьно розподілених генеральних сукупностей є величина F, подана виразом

Графік розподілу цього критерію для типових значень к

і к

зображено на

:у 3.12. Критична область будується в залежності від вигляду конкуруючої

ІИ.

Рис.

3.12

іглянемо перший випадок, коли нульовою гіпотезою є Н: D{X) = D(Y) а

)уючою - #,: D(X) > D(Y). У цьому випадку будують правобічну критичну

ь, для якої

дтичну точку F

(сс,

) знаходять із таблиці критичних точок розподілу

а-Снедекора (А^ - кількість ступенів довільності більшої дисперсії (див.

зк, табл. 5).

Елементи математичної статистики І'Л

Тоді правобічна критична область визначатиметься нерівністю

F >¥

q пр.

а область прийняття гіпотези такою нерівністю:

F < F

qnp.

Якщо обчислене значення критерію за формулою (3.66) є F

o64

< F , то немаї

підстав відхиляти нульову гіпотезу.

Якщо F

o64

> F

4np

, то нульову гіпотезу відхиляють.

Другий випадок.

Нульова гіпотеза є Н

: D(X) = D(Y) а конкуруюча - і/,: D(X)

О(У). У такому

випадку будують двобічну критичну область (див. Рис. 3.12).

Для отримання найбільшої потужності критерія потрібно, щоб виконувались

співвідношення

P(F<F,) = |; P(F< F

)=|

(3.6Н)

Через те, що таблиця критичних точок розподілу Фішера-Снедекора не мл<

лівих критичних точок, то знаходять тільки праву критичну точку

2 ~

qnp.

, k,, k

ос

за заданим рівнем значущості — і ступенями довільності k

'\k

. Що стосується

лівої критичної точки F

, то за методом введення спеціальної функції F' - j

сс

ймовірність події P(F < F,) =

—

замінюють ймовірністю

р /

— > —

F F,

= Р

У V

"І

Таким чином, ліва критична точка F - розподілу замінюється на праву

критичну точку F' - розподілу зі ступенями довільності k

, k

тобто достатньо

шукати тільки праву критичну точку

qnp.

, k

Ч У

де числа k

- кількість ступенів довільності більшої та меншої дисперсії

відповідно.

> Розділ

що F

o64

< то немає підстав відхиляти нульову гіпотезу, а якщо F

gfj4

> F,

ьова гіпотеза Я

- відхиляється.

иклад 10. Перевіримо тепер, чи можна вважати несуттєвими відхилення

ових дисперсій =0,250, (Я, =5); =0,108,(л

=6).

їв

'язання.

Сформулюємо гіпотези Я

: D(X) = D(Y), Я,: D{X) *D(Y).

Знайдемо числове значення критерія перевірки

<ї

р - о*

0,250

0,108

= 2,31.

За рівнем значущості а - 0,02, fc=5-l=4ifc=6-l = 5 знаходимо праву

шу точку двобічної критичної області

qnp.

, /С|, Arj

= 11,39

Оскільки F

g64

< F , то гіпотеза Я

приймається. Це означає, що різницю

бірковими дисперсіями можна пояснити випадковими причинами.

.6.6. Перевірка гіпотези про рівність дисперсії нормально розподіленої

генеральної сукупності деякому гіпотетичному значенню

іглянемо нормально розподілену генеральну сукупність із невідомою

)сією. При цьому є підстави припустити, що вона дорівнює деякому

:тичному) значенню <Tq .

же, перевіряємо таку нульову гіпотезу Я

: сг

=<jjj.

практиці така гіпотеза виникає тоді, коли потрібно перевірити точність

цв, інструментів, методів досліджень та стійкість технологій,

итерієм перевірки є

* =- (3.69)

іевідоме математичне сподівання генеральної сукупності і

2 П-Sl

X =—, (3.70)

- відоме.

на статистика має

- розподіл з k = п -

ступенями довільності у випадку

к = п ступенями довільності у випадку (3.70). Критична область, як відомо,

ься в залежності від конкуруючої гіпотези.

Елементи математичної статистики

І'Л

Перший випадок.

Нульова гіпотеза Н

:сг

конкуруюча - Я, :<т

<&1. У цьому випадку

будують правобічну критичну область, вимагаючи щоб ймовірність потрапляння

критерія в неї при справедливій нульовій гіпотезі дорівнювала прийнятому рівневі

значущості, тобто

Р[ХІ-

ІЧ

>Х

„

{(У.,Щ = а.

Іобч.

np.V-**i

'vj ^

•

(3.71 )

Критичну точку Хд

Пр

>к) знаходять із таблиці критичних точок

розподілу (див. Додаток, табл. 3). Тоді правобічна критична область визначає

і.ея

нерівністю

2 2

Хобч. Хі qnp.

а область прийняття гіпотези Я

такою нерівністю:

2 2

Хобч. ^ Xqnp. '

Отже, якщо Хобч. < Xqnp.>

т0

відхиляти гіпотезу Я немає підстав, а якщо

2 2

1/пр

, то гіпотеза Я

()

відхиляється.

Другий випадок.

2 _ „.2 .

Нульова гіпотеза Н

:а -а^; конкуруюча - Я,

двобічна критична область, для якої

сг

ФОІ.

Тут будується

Хобч.

Xа

X > Х

~2''

а ,

J „

V 7-І

(3.72)

Через те, що х

~ розподіл приймає тільки додатні значення і таблиця

критичних точок цього розподілу має тільки "праві" критичні точки, то

знаходження лівої критичної точки хілів. відбувається із використанням праної

критичної точки.

Оскільки події

2 2

X < Ха

І X

> Ха

^ q

ЛІН.

Л - /ь q пр.

є протилежними, то сума їх ймовірностей дорівнює одиниці

(х

<х1

1ів

) + р(х

>х

„

) = К

звідки на основі (3.72) маємо

P(x

<xL

.)=i-P(x

>xl

.)=i-

> Розділ

же, ліву критичну точку можна шукати так як праву, вважаючи, що

шість потрапляння критерія правіше цієї точки дорівнює

- у , тобто

;к

. X,

qnp

— •ь-

Що ХІ

лів

. < Х

0бч

. < X

qnp-

то гіпотезу відхиляти немає підстав, а якщо

ХІлів. і ХІбч. > Х

д„р., то нульову гіпотезу відхиляють.

;тій випадок.

и конкуруючій гіпотезі 7/, \а

<<Jq знаходять критичну точку

ХІБЧ.

'І К), то гіпотезу Н

приймають, інакше її відхиляють,

иклад 11. Із генеральної сукупності сформовано вибірку обсягом п - 13 і

;но виправлену вибіркову дисперсію Si =10,3. Необхідно за рівнем

цості ^ = 0,02 перевірити нульову гіпотезу Н

crfi

= 12 при

нативі Ну &Ф 12.

їв 'язання.

іходимо обчислене значення критерію

X обч.

(и -1)

•

(13-!)• 10,3

al ~ 12

= 10,3

и альтернативній гіпотезі Ну с?

12 критична область буде двобічною,

а таблицею критичних точок х

- розподілу (див. Додаток, табл.З)

,имо

/v (J лів

•

Л ц лів

І X,

Ч пр

3,57

\к

= Х

1Р

(0,01; 12) = 26,2,

рІВНЮЄМО ЦІ ТОЧКИ ІЗ Хобч. •

сільки 3,57 < 10,3 < 26,2, то гіпотеза Н

приймається (немає підстав її

ати). Інакше кажучи, виправлена вибіркова дисперсія =10,3 незначно

ЯЄТЬСЯ ВІД ГІПОТеТИЧНОЇ (Тц = 12 .

важення. Коли, знайдено вибіркову дисперсію за виразами

-•І (X,-X)

, або S

=I (х,-X)

•Q

п /=1 /=1

Елементи математичної статистики

І'Л

•„ . „ 2 ""

то за критерш перевірки приймають величину X - —у , яка також має

розподіл з k = п ступенями довільності. Вся подальша процедура є аналогічною

попередньому випадку.

3.6.7. Перевірка гіпотези про закон розподілу генеральної сукупності

Розглянуті в попередніх параграфах методи перевірки статистичних

гіпотез припускали відомою функціональну форму закону розподілу і

стосувались лише числових значень параметрів цього закону. Але є випадки,

коли самий вигляд закону розподілу є гіпотетичним і вимагає статистичної

перевірки.

Зображаючи у графічній формі статистичні ряди та порівнюючи полігони чи

гістограми із кривими розподілу відомих законів, можна уявити собі, принаймні

з якісного боку, про міру наближення теоретичного та емпіричного розподілів.

Користуючись відомими вже методами, можна вимагати перевірки гіпотези про

відповідність емпіричного розподілу (зображеного рядом розподілу, полігоном

чи гістограмою) деякому гіпотетичному (теоретичному), який описується

функцією розподілу F(x).

Нульовою гіпотезою Н

тут є твердження про те, що генеральна сукупність

підкоряється закону F(x). Для перевірки цієї гіпотези треба підібрати критерій.

Критерії перевірки гіпотези про закон розподілу називають критеріями

згоди. Вони базуються на виборі певної міри розбіжності між теоретичним і

емпіричним розподілами. Якщо така міра (критерій) для випадку, який

розглядається, перебільшує певним чином встановлену межу, то гіпотеза

відхиляється і навпаки.

Розглянемо деякі критерії згоди, які найчастіше використовуються в

практичних розрахунках.

Критерій

(Пірсона)

Припустимо, що наша гіпотеза цілком визначає вигляд функції розподілу,

хоча цей критерій застосовується і для статистичних досліджень.

Розіб'ємо область зміни випадкової величини Хна скінчену кількість інтервалів

А,, ..., A

i нехай р. - ймовірність для величини А'для даного розподілу F{x)

прийняти значення, яке належить /'-му інтервалові, а т. - кількість значень із

вибірки обсягом

(х,, х

,..., х

), які потрапили на інтервал А. Очевидно, що мають

виконуватись такі умови:

> Розділ

р, + р

+... + р, = 1,

1 2

' (3.73)

т, +т

+ ... +

Ш,

= п.

що гіпотеза, яка перевіряється, є вірною, тоді m

- частота появи події, яка

сному із п виконаних випробовувань Має ймовірність p..

же, ми можемо розглядати т. як випадкову величину, яка має біноміальний

розподілу з центром в точці пр. і зі середнім квадратичним відхиленням

де q, =1 -р,.

що п—то можна вважати, що частота події т. розподіляється

готично нормально з тими ж самими параметрами.

и вірності нашої гіпотези асимптотично нормально будуть розподілені (в

юсті) і нормовані величини

£,= ' ,{і = \,2...п) (3.74)

л/

'Л

-ЧІ

метрами (т^ = 0; а

(

= 1), які згідно зі співвідношеннями (3.73) пов'язані між

так:

о. (3.75)

/-1 /=1 Jn-Pi

міру розбіжності даних вибірки m

..., т

з теоретичними даними

,, ..., np

приймається величина

/=1 1=1 п

•

Рі

є х

~ розподіл зк = 1-с- \ ступенів довільності (с - кількість параметрів

цлу F(x), які оцінюються за вибіркою). Тому ця величина називається

іієм xj- ("хі-квадрат")

і=1 п

•

Рі

будуємо правобічну критичну область, вимагаючи, щоб ймовірність

шяння критерію в неї (при справедливості нульової гіпотези) дорівнювала

юму рівневі значущості а

Р[Х

>ХІ(аЛ)1 = а = і/

ке, критичною областю буде

Елементи математичної статистики

І'Л

а область прийняття гіпотези Н

є такою:

<Х

(ос,к).

Таким чином, якщо обчислене за виразом (3.76) значення критерію

<ХІ(

,к), то немає підстав відхилити гіпотезу Н

, а якщо X

>Xq(

-k), іо

нульову гіпотезу відхиляють.

2 ' (wij -

п • Рі

)

Зауваження!. Статистика X

2, має г

- розподіл при //-><«•.

м п

•

Рі

Тому необхідною умовою застосування критерію х

(Пірсона) є великий обсяі

вибірки і наявність у кожному інтервалі не менше 5 + 10 спостережень. Якщо їх

менше, то потрібно об'єднати інтервали.

Зауваження 2. Через те, що можливі помилки першого та другого роду, а

особливо, якщо маленькі різниці між частотами та ймовірностями (добра

погодженість теоретичного та емпіричного розподілів), потрібно обережно

робити висновки. Перед остаточним висновком слід ще раз перевірити критерій

на більшому за обсягом матеріалі, або використати ще інший критерій.

Критерій А.Н. Колмогорова

За міру розбіжності між теоретичним та емпіричним розподілом А.П. Колмогорон

розглядає максимальне значення модуля різниці між статистичною Г(.\) і

теоретичною F(x) функціями розподілу

D= max \F*(x)-F(x)\. (3.75)

Він показав, що при необмеженому зростанні обсягу вибірки п, якою б не

була функція розподілу F(x) випадкової величини X, ймовірність нерівності

D4n>X

прямує до границі

р(Х) = 1- £(-\)

-e-

2k2x

\ (3.76)

Функція р(Л) описана формулою (3.76), є протабульована і для неї складено

відповідні таблиці (див. Додаток, табл.6).

Величину D знаходять, або попередньо побудувавши графіки функцій F(.v) і

F*(x) в одній системі координат, або методом порівняння їх значень у заданих

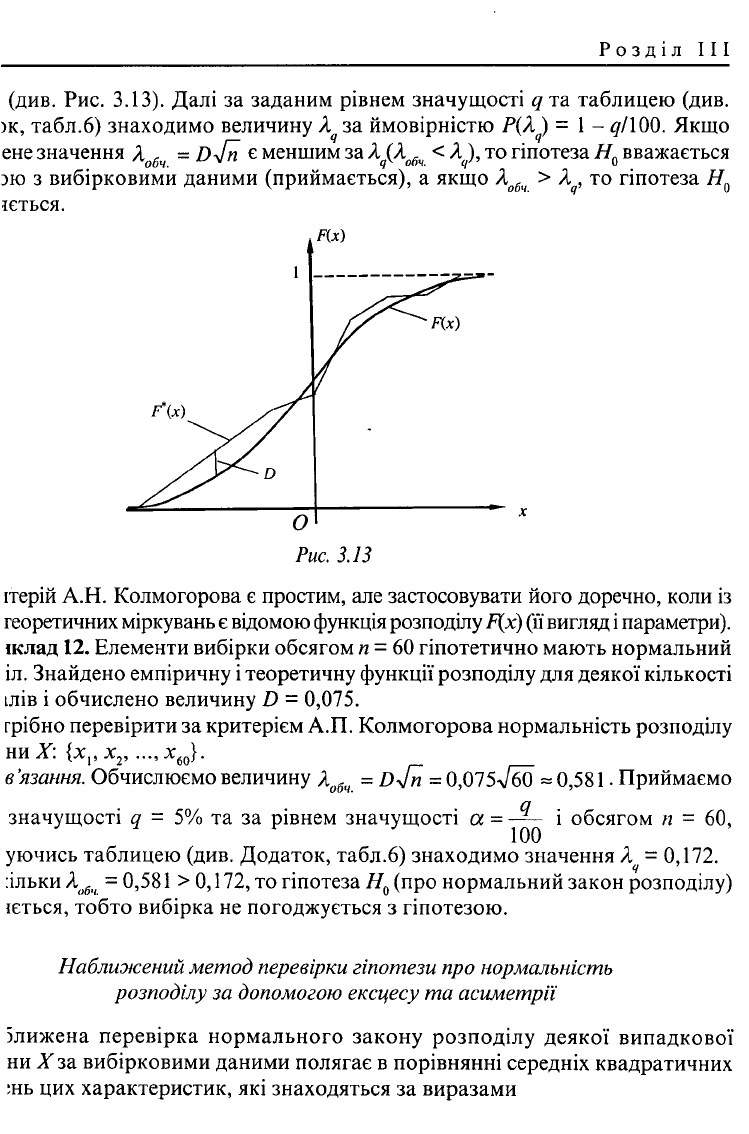
> Розділ

(див. Рис. 3.13). Далі за заданим рівнем значущості q та таблицею (див.

ж, табл.6) знаходимо величину А за ймовірністю Р(А

) =

- д/100. Якщо

ене значення А

обч

= о4п є меншим за

(А

ойч

), то гіпотеза Я

вважається

:>ю з вибірковими даними (приймається), а якщо Л

дбч

> А , то гіпотеза Я

ЇЄТЬСЯ.

ітерій А.Н. Колмогорова є простим, але застосовувати його доречно, коли із

теоретичних міркувань

відомою функція розподілу F\x) (її вигляд

параметри),

іклад 12. Елементи вибірки обсягом п = 60 гіпотетично мають нормальний

іл. Знайдено емпіричну і теоретичну функції розподілу для деякої кількості

ілів і обчислено величину D = 0,075.

грібно перевірити за критерієм А.П. Колмогорова нормальність розподілу

ниЛГ: {х,,х

, ...,х

в'язання. Обчислюємо величину А

обч

= D-Jn

0,075v60 ~ 0,581. Приймаємо

значущості q = 5% та за рівнем значущості а = у^ і обсягом ti = 60,

уючись таблицею (див. Додаток, табл.6) знаходимо значення

= 0,172.

:ільки А

ойч

= 0,581 > 0,172, то гіпотеза Я

(про нормальний закон розподілу)

іється, тобто вибірка не погоджується з гіпотезою.

Наближений метод перевірки гіпотези про нормальність

розподілу за допомогою ексцесу та асиметрії

Злижена перевірка нормального закону розподілу деякої випадкової

ни Хза вибірковими даними полягає в порівнянні середніх квадратичних

:нь цих характеристик, які знаходяться за виразами