Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань

Подождите немного. Документ загружается.

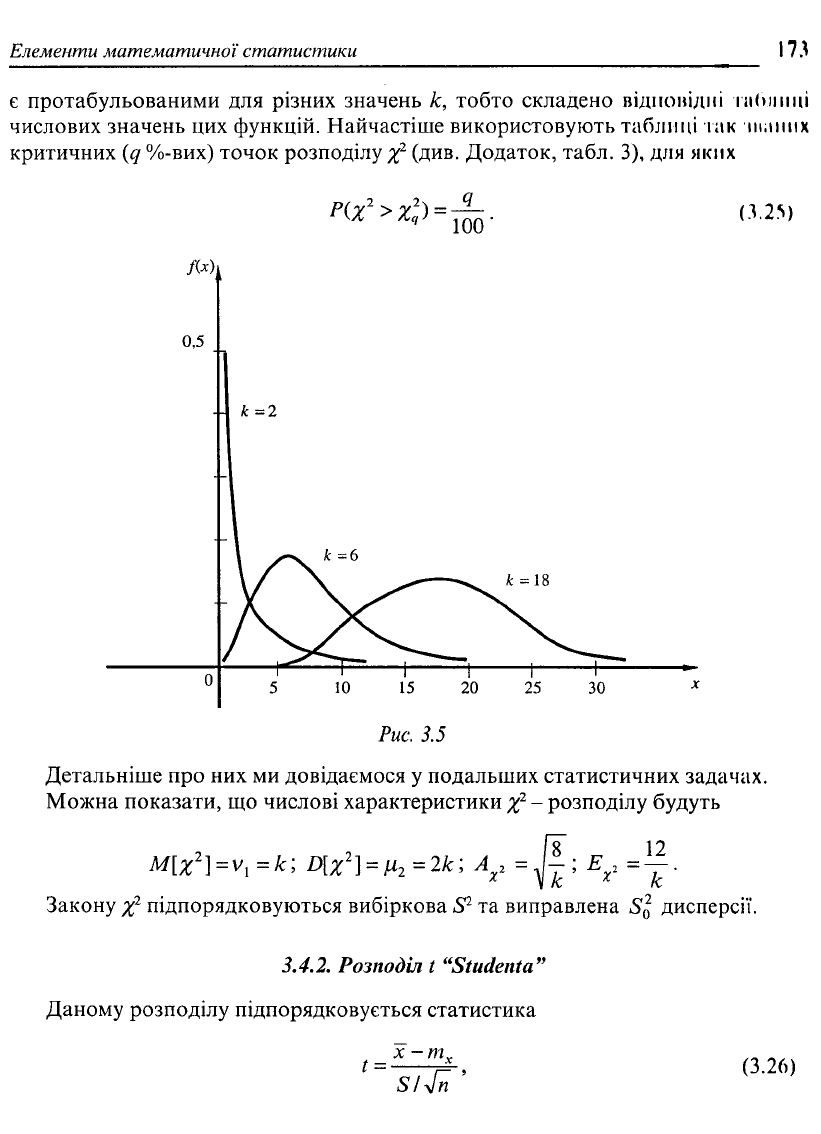
Елементи математичної статистики

І КІ

є протабульованими для різних значень к, тобто складено відповідні nihiiiini

числових значень цих функцій. Найчастіше використовують таблиці гак званих

критичних (q %-вих) точок розподілу

(див. Додаток, табл. 3), для яких

Р(Х

>Х!,) =

100'

(3.2.S)

Рис. 3.5

Детальніше про них ми довідаємося у подальших статистичних задачах.

Можна показати, що числові характеристики х

- розподілу будуть

Міх

} = У,=к; D[

] = ц

=2к; А

Закону х

підпорядковуються вибіркова S

та виправлена дисперсії.

3.4.2. Розподіл t "Studenta"

Даному розподілу підпорядковується статистика

/ =

S/л/й '

(3.26)

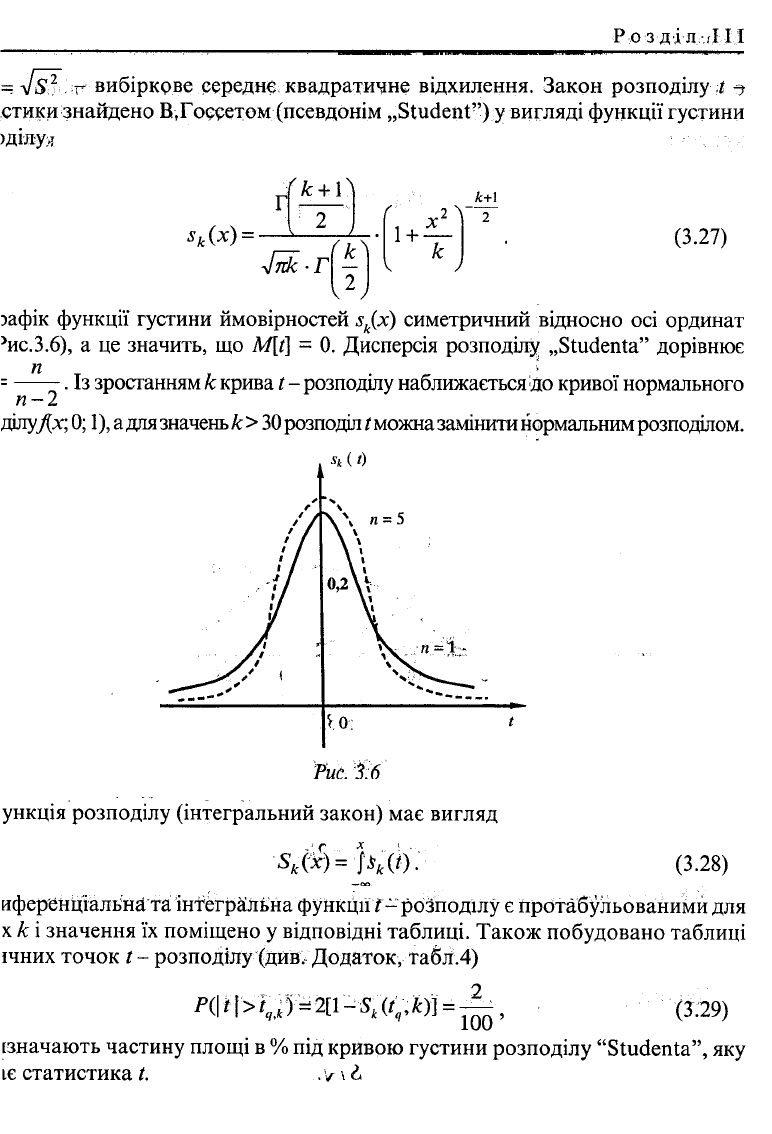
Розділ „' I 11

= yfs

:- вибіркрве середню квадратичне відхилення. Закон розподілу ^ ^

етики знайдено В, Госсетом (псевдонім „Student") у вигляді функції густини

щілул

*к(

)=-

к +1

°Jjtk

•

1 +

к+\

Л\~Т

(3.27)

зафік функції густини ймовірностей s

{x) симетричний відносно осі ординат

^ис.3.6), а це значить, що M[t] = 0. Дисперсія розподілу „Studenta" дорівнює

п •

= . Із зростанням к крива t - розподілу наближається до кривої нормального

—

ділуДх;

0; 1),

а для значень к> 30 розподіл t можна замінити нормальним розподілом.

(i)

Рис.

ункція розподілу (інтегральний закон) має вигляд

(x) = }*,(/)

•

(3.28)

иференціальна та інтегральна функції

- розподілу є протабульованими для

х к і значення їх поміщено у відповідні таблиці. Також побудовано таблиці

ічних точок t - розподілу (див,- Додаток, табл.4)

Р( \i\>t

mm-S

M = ^, (3.29)

ізначають частину площі в % під кривою густини розподілу "Studenta", яку

іє статистика t.

/ \ L

Елементи математичної статистики

І КІ

3.4.3. Розподіл F Фішера-Снедекора

Важливе застосування в дисперсійному аналізі має статистика F

рЛL

V '

(3.30)

де незалежні випадкові величини U і ^розподілені за законом^

А:,

і к

ступенями

довільності відповідно. Диференціальна функція розподілу, графік якої зображенії

рисунком 3.7 (густина ймовірностей випадкової величини F) має вигляд

о,

якщо х < 0,

М-2

х'

(3.31)

якщо х > 0,

ГЧ

V /

(к

+к

-х)

(3.31)

якщо х > 0,

а відповідна їй функція розподілу називається F- розподілом (або розподілом

Фішера-Снедекора) із к

та ^ступенями довільності, які є параметрами розподілу.

Таблиці (див. Додаток, табл.5) для F- розподілу використовуються такі, де

за відомими к

і к

можна знайти значення F, для якого

P(F>F

100'

(3.32)

тобто F - це q - відсоткова верхня межа розподілу F.

Як правило, використовують значення q = 5%, q - 2,5%, q = 1% зі широким

діапазоном величин

Аг,

і к

Розглянемо тепер практичне застосування наведених теоретичних розподіл

і н

у різних задачах математичної статистики.

§ 3.5. Оцінки параметрів розподілу за малими вибірками.

•

Довірчі інтервали

Оцінки невідомих параметрів розподілу, розглянуті в параграфі 3.3, виконано

за допомогою відповідних числових характеристик. Такі оцінки, як зазначено, с

точковими і їх використовують у вибірках великого обсягу (як відомо, для

Розділ III

:нтів таких вибірок виконується закон великих чисел). Для вибірок малих

гів числове значення оцінюваного параметра таким способом можна

мати тільки наближено. Похибка при цьому збільшуватиметься зі

іненням обсягу вибірки.

тже, для вибірок малих обсягів необхідно вказати точність і надійність

си, тому що точкові оцінки, у таких випадках є лише деякими випадковими

іинами.

,ля того, щоб мати точну і надійну оцінку в для параметра в потрібно для

-якого малого числа а > 0 вказати таке 5, щоб виконувалася умова

Р(\в -Є|< 5) = Р(-8 <0—6 <8) = Р(в-8 < 9 < в + 5) =

- а.(3.33)

[им меншим для даного а буде значення 8, тим точнішою буде оцінка в •

)тже, число Охарактеризує точність оцінки. Співвідношення (3.33)

нується з ймовірністюр =

- а. Тобто, можна сказати, що ймовірність того,

нтервал (в - 8; в + 5) із випадковими кінцями накриває (як говорять в

гистиці) невідомий параметр в, дорівнює 1 - а. Такий інтервал називають

ірчим і н т е р в а л о м , а ймовірність (1 - а) - д о в і р ч о ю ймовір-

т ю. Довірча ймовірність (її позначають у) характеризує надійність

ки і вважається досить близькою до одиниці (у= 0,95, 0,98, 0,999).

^обто інтервал (в - 8; в + 8 ) буде довірчим інтервалом для

іметра в тільки з певною довірчою ймовірністю у.

'озглянемо побудову довірчих інтервалів для деяких параметрів нормально

юділеної генеральної сукупності.

3.5.1. Довірчий інтервал для оцінки центра розподілу

при відомому параметрі о

Техай кількісна ознака X генеральної сукупності розподілена нормально з

иною розподілу / (х, т

, о

). При цьому є відомим параметр о\ Необхідно

гати невідомий параметр т

за вибірковим середнім х .

Зтже, треба знайти (побудувати) довірчий інтервал, який накриває невідомий

аметр із певною надійністю у.

Вибіркове середнє х з відомих причин розглядатимемо як випадкову величину.

Якщо випадкова величина ^розподілена нормально з параметрами т

, а

, то

іркове середнє Зс, яке знайдено з окремих значень х, = (/ =

п) величини X

ож має нормальний розподіл з параметрами т

і aj4n.

Розглянемо ймовірність події

Р(\х - т

\ < 5) = у,

(3.34)

Елементи математичної статистики

І КІ

яку для нормального розподілу знайдемо, використовуючи функцію Лампас.і,

тобто

Р(\х -m

\<S) = 20

(Z),

де z =

у—

- аргумент функції Лапласа,

Уг

УІП

звідки

5 = Z-^L і P(|3t -m

| < Z

-f=) = 20

(Z),

ЛІП уІП

або

Р(х - Z?-~= <т < х = у. (3.35)

Jn 4п

Отже з надійністю у можна стверджувати, що довірчий інтервал (х - Z -0

;

а п

\Іп '

х +Z

—j=)

накриває невідомий параметр т , а точність оцінки - 8- Z.

УІП

yfn

Значення функції

<J>

(Z)

знаходиться з таблиці для функції Лапласа за обраною

довірчою ймовірністю /

(див.

Додаток, табл. 2).

Зауважимо, що:

1) для фіксованого значення z, а значить зі збільшенням обсягу п, точність

інтервального оцінювання збільшується;

2) збільшення надійності оцінки у -

2Ф

(2Г)

веде до збільшення Z, оскільки

функція <£>

(Z) є неспадною, а тому для фіксованого обсягу п величина 5 зростає,

що приводить до збільшення довжини довірчого інтервалу, а значить, і до

зменшення точності оцінки 5;

3) близькість до одиниці довірчої ймовірності встановлюється величиною

а(у

1 - а), яка є q %-ою критичною точкою відповідного розподілу, а =

(див. § 3.4). Наприклад, якщо у= 0,96, тоді а = = 0,04 . Це означає, що тільки

у 4 % вибірок оцінюваний параметр не буде знаходитися у довірчому інтервалі, а

у 96 % вибірок цей інтервал буде містити в собі невідомий параметр.

Приклад 1. Випадкова величина X має нормальний розподіл зі середнім

квадратичним відхиленням ст. = 2. Знайти довірчий інтервал для оцінки

математичного сподівання т

за вибірковим середнім д: =41,якщо«= 16, у= 0,95.

Розділ III

зв'язання. Запишемо вираз для довірчого інтервалу

/ \

х -

yjn -Jn

таблицею для функції Лапласа із використанням рівності у = 2Ф

(г)

цимо z = 1,96. Обчислимо значення виразу = 0,98. Тоді довірчий

УІП

ал буде (Зс -0,98; х + 0,98).

же, у 95 % невідоме математичне сподівання міститься в інтервалі

3,12 <т

<5,08.

чність оцінки буде 8 = 0,98.

іиклад 2. Знайти мінімальний обсяг вибірки, якщо необхідна точність 8 = 0,5

іа у порівнянні з попереднім прикладом) для надійності у= 0,95 і середнього

ітичного відхилення

<Т.

= 2.

зв'язання. Використовуємо вираз 8 - , звідки п = —~ 62.

•J п 8

ким чином, збільшення точності (зменшення величини 5) веде до суттєвого

іення обсягу вибірки.

.5.2. Довірчий інтервал для оцінки центра розподілу при невідомому сг.

і у попередньому випадку, скористаємося точковою оцінкою х для

іатичного сподівання т

. Замість невідомого а

можна використати

сове середнє квадратичне відхилення S або S

(незміщену оцінку). Величини

— YYI

як відомо, мають

- розподіл. Тоді можемо знайти величину t = j=-,

SNn

іє розподіл „Studenta" з k = п -

ступенями довільності.

же, для ймовірності у =

- можна за таблицею (див. Додаток, табл.4)

\ q %-ні межі ± t

, для яких

тлі x-m

I, q

P\-t .< <t .1 = 1- —

S/Ji 100

^ * mo

або P\x-t

<x-t

=\ = 1-^ (3.36)

Елементи математичної статистики

І КІ

для будь-якого т

Отже, інтервал

x-t

q,k

•In

+ t

qjc

yfn

(3.37)

цілком накриває математичне сподівання т

Приклад 3. Побудувати довірчий інтервал для оцінки математичної о

сподівання т

, якщо п = 9; у = 0,95; х = 6; S

= 3.

Розв'язання. Із використанням інтервалу (3.37) шукані межі будуть

S .

q.k Г- і

X П

q,k І- '

УІП

За таблицею критичних точок розподілу „Studenta", числом k - 9 18

(кількістю ступенів довільності) і <//100 = 1 - у - 0,05 знаходимо t

= 2,31.

У результаті отримаємо

6-2,31-^<ш <6 + 2,31-^=,

V9 " V9

або

3,69 <т

<8,31.

Тепер для порівняння обчислимо межі довірчого інтервалу за допомогою

критичних точок нормального розподілу, вважаючи, що S = сг.. Тоді за таблицею

функції Лапласа знаходимо z = 1,96 і довірчий інтервал буде

о",. _ а

x-z—£= < т

< x+z—,= ,

УІП УІП

або

4,04 < т

< 7,96.

Довжина інтервалу за розподілом „Studenta" 8,31 - 3,69 = 4,62 є більшою за

довжину, отриману за нормальним розподілом 7,96 - 4, 04 = 3,92. Здавалося б,

що остання оцінка краща, але вона зроблена у припущені виконання рівності

S = <7., якої взагалі не існує. Тому нормальний розподіл у цьому випадку штучно

звужує інтервал, а оцінка, проведена за розподілом „Studenta", використовуючи

достовірну інформацію, є об'єктивнішою.

Розділ III

3.5.3. Довірчий інтервал для оцінки дисперсії і

середнього квадратичного відхилення

озглянемо нормально розподілену величину X. Потрібно побудувати

ічий інтервал для невідомої дисперсії генеральної сукупності за вибірковими

нками S

або Sg. Відомо, що обидві оцінки мають %

- розподіл з /с = п - 1

:нями довільності,

апишемо вираз для S

=~t(x

-x)

п /=1

;мо позначення (х,. -х)

=vv? і утворимо рівність

n-S

= X

/=1

юділимо на а

5>,

_ і=і

Ірава та ліва частини в отриманій рівності мають у; - розподіл з k = п - 1

енями довільності, оскільки а\ - стале число, а чисельники є сумами квадратів

іих величин.

Іобудуємо довірчий інтервал для дисперсії із використанням величини у .

цього з обраною довірчою ймовірністю у=

- «запишемо

2 ^

nb 2

СТ

= 1-а.

1а графіку х

- розподілу (див. Рис. 3.7) це можна зобразити так:

/И

(3.38)

Елементи математичної статистики

КІ

Тобто величина —j- займає певну площу під кривою густини

х~

ро іноді ну,

2.2 .

обмежену двома ординатами в точках Х\ 1X2- При цьому слід нам яташ, ию

точки можуть змінювати своє положення, а площа буде сталою (вона зада<

м я

ймовірністю у= 1-а).

Величини Хі і х\ вибирають так, щоб виконувалась умова

Р(Х

<Х') = Р(Х

<ХІ) = J, 0.34)

тобто ймовірність виходу величини, яка має х

~ розподіл, за межі відрізка

7 2

[Х, ; Хи

однаковою як ліворуч, так і праворуч, і дорівнює — (а визначає

</%-

н у

критичну точку розподілу статистики х

)- Далі з врахуванням рівності (3.34)

запишемо

< — <Х

г =1 -Р(Х

<Х

)-Р(Х

<Х

г). (3.40)

' J

Оскільки площа під кривою Х

~ розподілу фіксується ліворуч ймовірнісно

Р(Х > Х\), то її можна розглядати як ймовірність протилежної події в поріїїпяппі

з ймовірністю Р(х

< Хі)

тобто

Р(Х

>ХЇ) = і-|.

Інакше кажучи, q %-ні критичні точки - розподілу визначатимуться

а . .а

ймовірностями ліворуч і — праворуч.

Тепер, перетворимо нерівність

хі <~~г<х2

(ТІ

так, щоб можна було оцінювати сг

Розглянемо, дві еквівалентні нерівності

2 2

Х\ <

та . <

Х2 >

які запишемо у вигляді

Розділ III

nS 2 nS 2

—т->(УІ та —

'єднаємо в одну нерівність

Хг

оді

2 nS

Х2 Х\

<—г

<Хг

= Р

2 < °х < 2

ХГ Х\

= 1-а

(3.41)

nS . . ... ...

>тже —y ' —Т Д°

В1

ЧИМ

інтервалом для невідомої дисперсії а

Х2 Х\

(ля середнього квадратичного відхилення матимемо

S\fn

<(J к

SJ*

\[ХГ \l~XI

= 1-а

(3.42)

\fn Sjn

довірчии інтервал для середнього квадратичного відхилення.

Триклад 4. Побудувати довірчий інтервал з надійністю у = 0,96 для невідомої

іерсії генеральної сукупності спостережень випадкової величини X,

юділеної нормально, за вибіркою із обсягом п = 20 та відомою виправленою

рковою дисперсією SQ = 10.

^озв 'язання.

. За довірчою ймовірністю у = 0,96 обчислимо такі величини:

у =

- а = 0,96, а = 0,04, а /2 = 0,02.

Де означає, що Р(

> Z

) = ~ = 0,02 , а Р{% > *,

) =

- - = 0,98 .

І. Обчислимо КІЛЬКІСТЬ ступенів ДОВІЛЬНОСТІ

ДЛЯ

величини SQ

к = п -

= 19.

). За таблицею критичних точок %

- розподілу, ймовірностями Р(х

> Х

) =0,02,

> Х\) =0,98 і числом к =19 знаходимо = 33,7 , %] = 8,6 .