Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань

Подождите немного. Документ загружается.

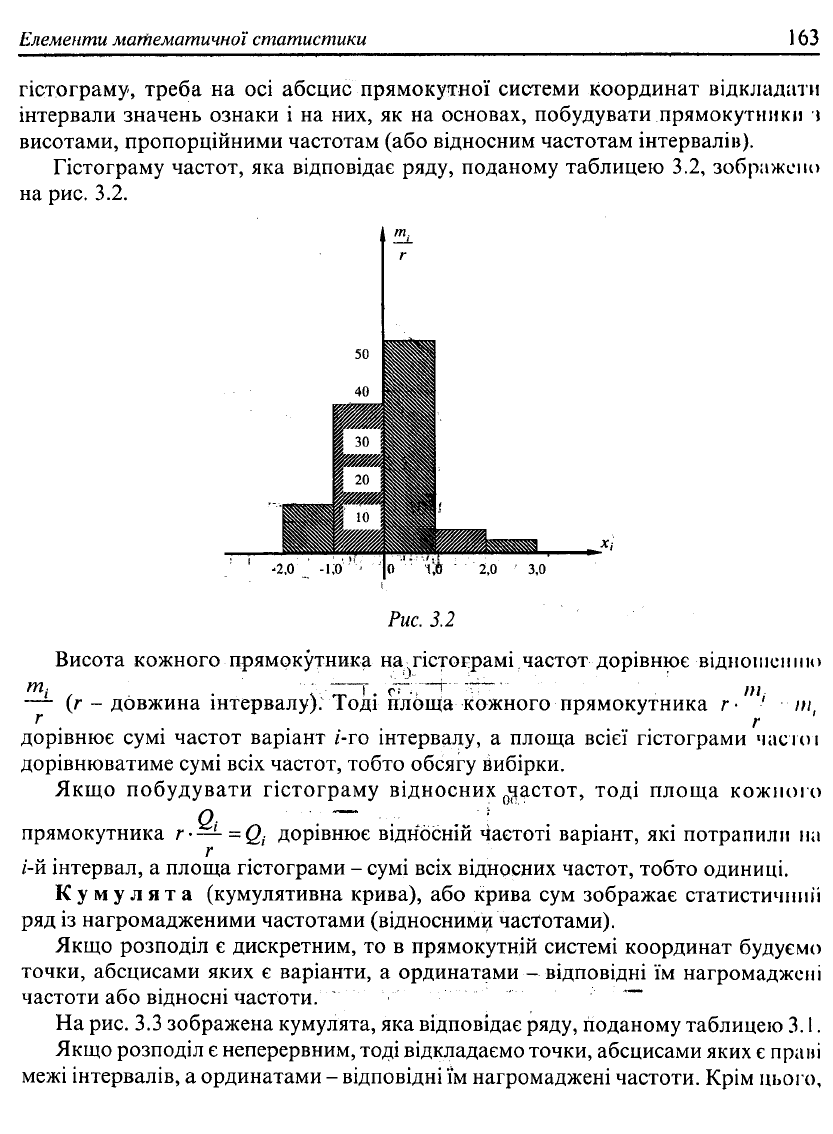
Елементи математичної статистики

І КІ

гістограму, треба на осі абсцис прямокутної системи координат відкладати

інтервали значень ознаки і на них, як на основах, побудувати прямокутники з

висотами, пропорційними частотам (або відносним частотам інтервалів).

Гістограму частот, яка відповідає ряду, поданому таблицею 3.2, зображено

на рис. 3.2.

т.

Рис.

3.2

Висота кожного прямокутника на ^гістограмі частот дорівнює -відношенню

—'- (г-довжина інтервалу). Тоді плбща кожного прямокутника /••'"' пі

... . г

дорівнює сумі частот варіант /-го інтервалу, а площа всієї гістограми частої

дорівнюватиме сумі всіх частот, тобто обсягу вибірки.

Якщо побудувати гістограму відносних ^астот, тоді площа кожного

прямокутника r-— = Q

дорівнює відносній частоті варіант, які потрапили на

/-й інтервал, а площа гістограми - сумі всіх відносних частот, тобто одиниці.

Кумулята (кумулятивна крива), або крива сум зображає статистичний

ряд із нагромадженими частотами (відносними частотами).

Якщо розподіл є дискретним, то в прямокутній системі координат будуємо

точки, абсцисами яких є варіанти, а ординатами

—

відповідні їм нагромаджені

частоти або відносні частоти. "

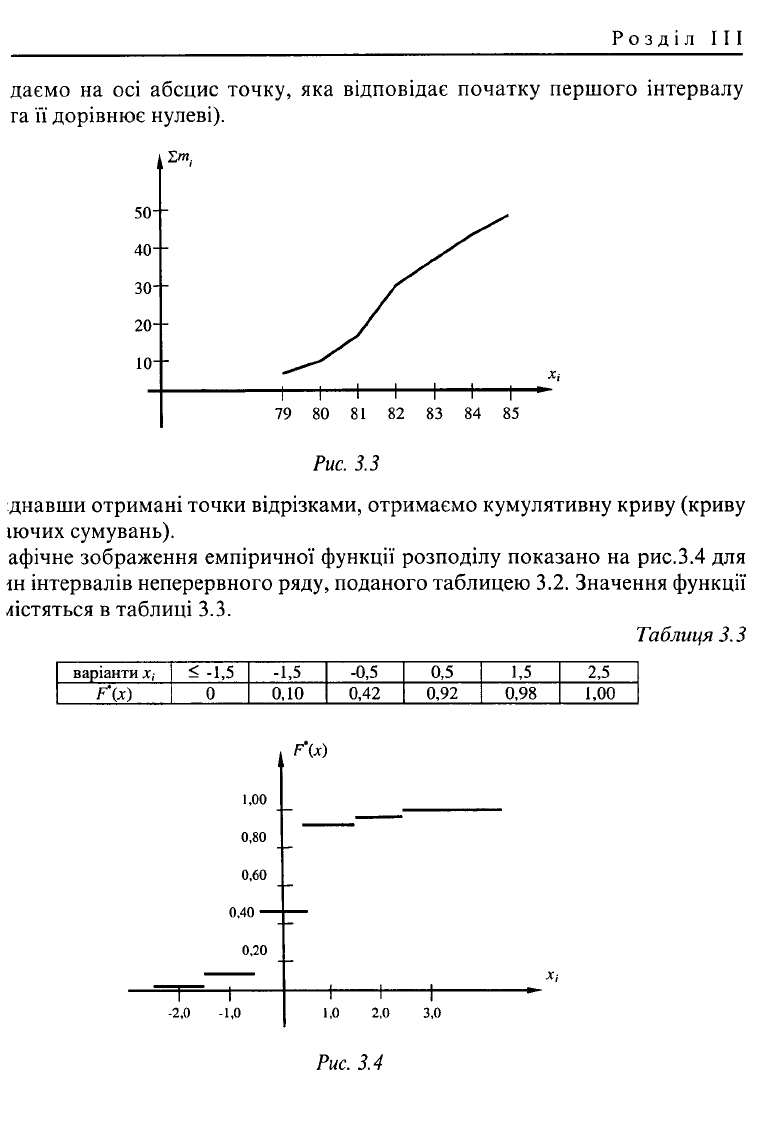
На рис. 3.3 зображена кумулята, яка відповідає ряду, поданому таблицею 3.1.

Якщо розподіл є неперервним, тоді відкладаємо точки, абсцисами яких є прані

межі інтервалів, а ординатами - відповідні їм нагромаджені частоти. Крім цього.

Розділ III

даємо на осі абсцис точку, яка відповідає початку першого інтервалу

та її дорівнює нулеві).

Рис. 3.3

днавши отримані точки відрізками, отримаємо кумулятивну криву (криву

іючих сумувань).

афічне зображення емпіричної функції розподілу показано на рис.3.4 для

ш інтервалів неперервного ряду, поданого таблицею 3.2. Значення функції

лютяться в таблиці 3.3.

Таблиця 3.3

варіанти

х,•

< -1,5 -1,5

-0,5 0,5

1,5

2,5

Пх)

0,10 0,42

0,92

0,98 1,00

Ґ(х)

1,00

0,80

0,60

0,40 —

0,20

-2,0 -1,0 1,0 2,0 3,0

Рис. 3.4

Елементи математичної статистики

І КІ

Побудова статистичного ряду-це перший крок до осмислення спостережеш..

Однак на практиці цього буває недостатньо, особливо коли виникає необхідність

порівнювати ряди спостережень. Такі ряди можуть бути однотипними за формою

при графічному зображенні, але відрізнятися значенням ознаки, відносно якої

групуються результати спостережень, або мірою розсіювання, тобто псиними

кількісними характеристиками.

Відзначимо, що для будь-якого розподілу вибірки можна обчислити псі

характеристики, а саме положення центра групування, розсіювання, асиметрію,

ексцес і т.д. Ці характеристики називають емпіричними або вибірковими,

оскільки вони отримуються зі спостережень і змінюватимуться від вибірки до

вибірки.

§ 3.3. Статистичні оцінки параметрів розподілу

За так званою "основною теоремою математичної статистики" вважається,

що вибіркові характеристики є статистичними оцінками теоретичних

характеристик (параметрів) розподілу.

Наприклад, середнє значення з вибірки обсягом п (середнє арифметичне)

Х\ "1" 0С-) ... "Ь

х„

х =— -

будемо вважати оцінкою математичного сподівання М[Х\ випадкової величини

X, якщо варіанти вибірки х,, х

, ... х

розглядати як окремі реалізації

(спостереження) цієї випадкової величини. Середнє арифметичне є лінійною

функцією результатів спостережень.

Будь-яка функція результатів спостережень, яка не залежить від невідомих

параметрів, називається статистикою.

Отже, статистика, яка отримана за результатами спостережень і за якою можна

судити про невідоме істинне значення параметра 0, називається оцінко ю

параметра 0.

Таким чином, в загальному випадку задачу знаходження оцінок параметрів

теоретичних розподілів можна сформулювати так: розглядається випадкова

величина X, яка підпорядковується деякому теоретичному закону розподілу

F(X, 0), аналітичний вигляд якого є відомим, а0- параметр закону розподілу,

числове значення якого є невідомим. Провести дослідження для всієї генеральної

сукупності неможливо і тоді про параметр ©намагаються судити за вибірками і

цієї сукупності.

Отже, із генеральної сукупності розглянемо т вибірок, кожна із яких

складається з п незалежних спостережень за об'єктом (і = 1,2, ... п)

Розділ III

лі вважають, що кожна вибірка - це окремі значення випадкових величин

1, 2 ... т), які мають закон розподілу F (X, 0). Тоді деяка однозначно

ієна функція результатів спостережень над випадковою величиною X

оцінкою параметра 0, яку називають точковою,

озуміло, що не кожна статистика може бути оцінкою певного теоретичного

етра. Оскільки результати досліджень випадкові, то будь-яка статистика є

ковою величиною. Для того, щоб статистика могла служити оцінкою

го параметра 0, необхідно, щоб розподіл цієї статистики був зосередженим

гньо близько від невідомого параметра 0, тобто так, щоб ймовірність

их відхилень статистики від 0 була малою. Тоді при систематичному

туванні цієї статистикою як параметром в середньому буде досягатися

ідна точність. Бажано також, щоб при збільшенні кількості спостережень

:ть результатів оцінювання також збільшувалась.

ія цього оцінки параметрів мають відповідати умовам незміщеності,

іості (обгрунтованості) та ефективності.

цнка 0 параметра 0 називається незміщеною, якщо її математичне

зання дорівнює параметру, який оцінюється, тобто

сщо рівність (3.7) не виконується, тоді оцінка 0 може або збільшувати

ння параметра 0, (М[0]>0), або зменшувати його (М[0]<0). В обох

,ках це приводить до систематичних похибок при користуванні оцінкою 0

гь параметрів. Таким чином, вимога незміщеності гарантує відсутність

уіатичних похибок при користуванні оцінкою 0.

лушною (обгрунтованою) називають таку статистичну оцінку,

;ля п—прямує за ймовірністю до оцінюваного параметра, тобто

рядковується закону великих чисел

гже, слушність оцінки свідчить про те, що чим більшим є обсяг вибірки, тим

іа ймовірність того, що похибка оцінки не перевищує як завгодно мале

не число є. Ця властивість більше придатна для вибірок великого обсягу.

e = f(x

,...x

)

(3.6)

М[0] = 0.

(3.7)

lim Р(|0-0|<є) = 1.

(3.8)

Елементи математичної статистики І КІ

Ефективною оцінкою називають таку, яка для заданого обсягу вибірки н

має найменшу дисперсію серед всіх можливих незміщених і обгрунтованих оцінок

параметра. Якщо 0 іГ - дві незміщені оцінки параметра 0 із дисперсіями /)|0|

і D[T], причому D[&] < D[T], тоді оцінка 0 буде ефективнішою оцінкою

параметра 0, тому що їй відповідає менше розсіювання окремих значені,

результатів спостережень навколо центра розподілу. Точкові оцінки, ям

задовольняють умовам незміщеності, обгрунтованості та ефективної-1 і,

називаються "найкращими".

Для отримання "найкращих" оцінок є різні методи, серед яких найбільш поши-

рені метод найбільшої правдоподібності (МП-метод).

запропонований Ґауссом та узагальнений Фішером, і метод м о м е и і і и ,

розроблений Пірсоном.

Розглянемо вибірку х

, ..., х

, обсяг якої дорівнює п, значень деякої

випадкової величини Xіз функцією густини ймовірностей/(х, 0), яка залежи

11,

від параметра 0. Тоді функція, яка має вигляд

Цх

,х

,...х

,в) = /(х

,в)/(х

,в).../(х

,в), (3.9)

називається функцією правдоподібності.

Нехай А'-дискретна випадкова величина, яка набуває значень £

,...,<!; із

(

частотами m

, ...,т

відповідно | Era, = п і F(X = /Д0).

V '

У цьому випадку функція правдоподібності матиме вигляд

цв) = .Г (0)/

тз

(0)--./Л (©)

(З.і о)

Вважатимемо значення відомими та розглянемо L(0) як функцію

невідомого параметра 0. Значення параметра 0, для яких функція правдоподібнос

і і

набуває максимуму, називають оцінками максимальної правдопо-

дібності.

Виявляється, що для досить загальних умов, що накладаються на

функцію розподілу, ці оцінки є асимптотично незміщеними, слушними і

ефективними.

Згідно відомих правил диференціального числення для знаходження оцінки

максимальної правдоподібності необхідно розв'язати рівняння

^ = 0 (3.11)

і вибрати такий розв'язок 0 =0 (JC,,X

, ..., х

), при якому функція L(0) набуває

максимуму.

Замість рівняння (3.11) зручніше розглядати рівняння вигляду

Розділ III

1 dL d\nL

тж^в-

(ЗЛ2)

и до уваги не саму функцію (3.9), а її натуральний логарифм.

кщо є два параметри 0, і 0

, то оцінки їх визначаються зі сумісного

азування двох рівнянь

31nL

. 91nL

= 0 і = 0.

30, 80

іайдемо оцінки параметрів нормального розподілу, користуючись МП-

JOM.

ехай за даними вибірки х

, ..., х

обсягу п спостережень нормально

зділеної випадкової величини X необхідно оцінити два параметри цього

іу m та а.

даному випадку функція правдоподібності L визначається співвідношеннями

( і

f(n-m;a) = L(x

,...,x

;m-,C7) =

2 а

(3.13)

, ,

. _ п , 2 Ід, ч2

In L = — ln 2 п — ln а

£(х,. -m)

2 2 2а м

[ля знаходження оцінок m і о

, продиференціюємо вираз (3.13) по m і о

та

лвняємо до нуля отримані вирази. У результаті отримаємо

31nL 1 "

— = = 0,

от а /=і

31nL « Ід,

да

2а

/=і

ки із першого рівняння матимемо

Х(*,->иГ= 0

Ех,.

т = =

(3.14)

фугого рівняння отримаємо

=-t{Xi-m)

. (3.15)

Пі=і

Елементи математичної статистики

І КІ

Отже, оцінкою математичного сподівання т є середнє арифметичне л , а

оцінкою дисперсії о

величина S

, яка називається вибірковою диспер-

сією. Метод найбільшої правдоподібності на практиці часто приводи її. до

необхідності розв'язувати доволі складні системи рівнянь. Він не завжди даі

оцінки, які є "найкращими".

Розглянемо метод моментів, запропонований К. Пірсоном. Моменти вибірки

вважаються оцінками для моментів розподілу величини X , які залежать від

невідомих параметрів. У свою чергу параметри, які оцінюються, можна знай

і н

вигляді певних функцій від теоретичних моментів, замінивши які їх оцінками,

тобто моментами вибіркового розподілу, ми і отримаємо оцінки для невідомих

параметрів.

Слід відзначити, що метод моментів іноді приводить до малоефективних

оцінок.

Отже, якщо вважати середнє арифметичне початковим вибірковим момеп

ом

першого порядку

. - 1 "

V, = * = -

Ех,,

п /=1

а вибіркову дисперсію S

центральним вибірковим моментом другого порядку

Ik-І(х,.-х)

п /=1

то, записуючи вирази для таких моментів будь-якого порядку

v^ =-•£*,* (k = 2,3,...), (3.16)

п м

(І = 3,4,..), (3.17)

п /=1

можна отримати оцінки інших параметрів розподілу випадкової величини X.

У вибірках великого обсягу, коли варіація ознаки вважається неперервною,

для знаходження оцінок параметрів користуються інтервальним статистичним

рядом. Тоді статистичні оцінки обчислюють за такими наближеними формулами:

[x] = ix-Q

, (3.18)

І=І

і=1

(3.19)

Розділ III

(3.20)

/=і

Ї^Ші-mjQ,. (3.21)

1=1

виразах (3.18)-(3.21) 5c - середина г'-го інтервалу; к - кількість інтервалів; (*)

ака статистичної оцінки.

Іайкращою" в сенсі незміщеності, слушності та ефективності є середнє

метичне як оцінка математичного сподівання.

ійсно, якщо х,, х

, ..., х - незалежні спостереження величини X, тоді

М[х] = М

1 "

— М[х

+Х

+ ... + Xj :

1 1 1 "

= -(M[x

] + M[x

] + ... + M[x

]) = -(x

+х

+ .„ + * ) = _\Ч =М[х]

п п п

/=1

тже, середнє арифметичне х є незміщеною оцінкою математичного

вання. За законом великих чисел відомо, що х також є слушною оцінкою

= 1-5 .

исперсія середнього арифметичного D[x] = —^ є найменшою серед дисперсій

нших можливих оцінок математичного сподівання. Тому х можна вважати

тивною оцінкою математичного сподівання т

, особливо, якщо х

ірядковується нормальному закону розподілу.

1 А

<є

п /=1

ибіркова дисперсія S -

—

£(Х

(

- - х) не буде незміщеною оцінкою дисперсії

п /=1

•альної сукупності (тобто теоретичного параметра <г).

озглянемо Х

, Х

, ..., Х

- взаємно незалежні випадкові величини з

натичними сподіваннями

М[Х

] = М[Х

] = ... = М[Х

] = т

сперсіями

D[X

] = D[X

] = ... = D[XJ = a

дайдемо математичне сподівання М[5

збразимо вибіркову дисперсію у вигляді

Елементи математичної статистики

І КІ

=-f

-X)

=^(X

-m

x +

-X)

ИІТ ПІТ,

= --^[(Х.-т

)-(Х-т

)]

п tt

Після нескладних алгебраїчних перетворень знайдемо математичне споді

паї мій

отриманого виразу

M[S

] = M

-Ьх.-mf

п і=1

-М[Х-т

]

П-\

= --па

- = а

п п п

Отже, оцінка S

є зміщеною оцінкою параметра а\ . Для того, щоб отрима

незміщену оцінку дисперсії, треба зміщену помножити на величину , (ця

п 1

величина називається поправкою Бесселя). Тоді величина

=-^S

=-1-Зс)

(3.22)

п -1 п -1 ;=і

є виправленою дисперсією і незміщеною оцінкою дисперсії гт;

генеральної сукупності. Такою оцінкою користуються більше для вибірок малих

обсягів.

Отже, для вибірок великих обсягів статистичні оцінки теоретичних параметрів

є асимптотично незміщеними, слушними і ефективними. Якщо обсяги вибірок (

малими (п < ЗО), то порушуються властивості "найкращої" оцінки. Відзначимо

також, що раніше розглядалося поняття відносної частоти події. Зрозуміло, що

відносна частота події є статистичною оцінкою ймовірності події.

171

Дійсно, з огляду на обмеженість класичної формули р

— для обчислень

ймовірностей випадкових подій, ми фактично обчислюємо статистичні оцінки

цих ймовірностей у багатьох практичних випадках.

§ 3.4. Точні розподіли деяких вибіркових характеристик

Якщо оцінки параметрів знаходяться з генеральної сукупності окремих значень

випадкової величини X, яка підпорядковується нормальному закону розподілу,

то це ще не означає, що самі оцінки (а вони, як зазначено раніше, також є

Розділ III

цсовими величинами) мають теж нормальний розподіл. Через те, що оцінки

летрів використовуються для розв'язування багатьох статистичних задач,

ібно знати точні закони розподілу хоча би головних вибіркових

стеристик (статистик). До таких законів відносяться розподіли %

(хі -

)ат), t - розподіл ("Studenta"), F- розподіл (Фішера).

3.4.1. Розподіл X

аний розподіл має випадкова величина, яка є сумою квадратів незалежних

цкових величин, які підпорядковуються нормальному закону розподілу з

етичними сподіваннями т

= 0 та дисперсіями а

=1 (/ =

п)

=Х

+Х

+...+Х

=ІХ

1=1

юзподіл (хі - квадрат розподіл) задається функцією густини ймовірностей

ш-

2°'

5/с

-Г(0,5к)

0, якщо х < 0,

(3.23)

е-°'

5х

-х

, якщох>0,

(х) = \t

є 'dt - гама-функція, к - число, пов'язане з обсягом вибірки п і

вається "кількістю ступенів довільності". Число к визначається як різниця

<ількістю випадкових величин (обсягом вибірки п) і кількістю зв'язків між

і (лінійних співвідношень).

[априклад, завжди існує таке співвідношення між випадковими величинами,

гворюють вибірку:

_ п

пх = £х,. ,

_ 1=1

іьки середнє арифметичне х є оцінкою центра розподілу т

. Тому для ^ -

оділу к = п - 1.

з виразу (3.23) видно, що густина

- розподілу залежить тільки від одного

метра п (або к). Графік функції/Дх) для різних значень к показано на рис.3.5.

рисунка видно, що

у?

- розподіл розташовано праворуч від початку координат

більшенням к він наближається до нормального розподілу. Функція^, (х), а

ж інтеграл ймовірностей

(x) = P(

>Xo)= j f

Mdx (3.24)

Ха