Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань

Подождите немного. Документ загружается.

Елементи теорії ймовірностей 121

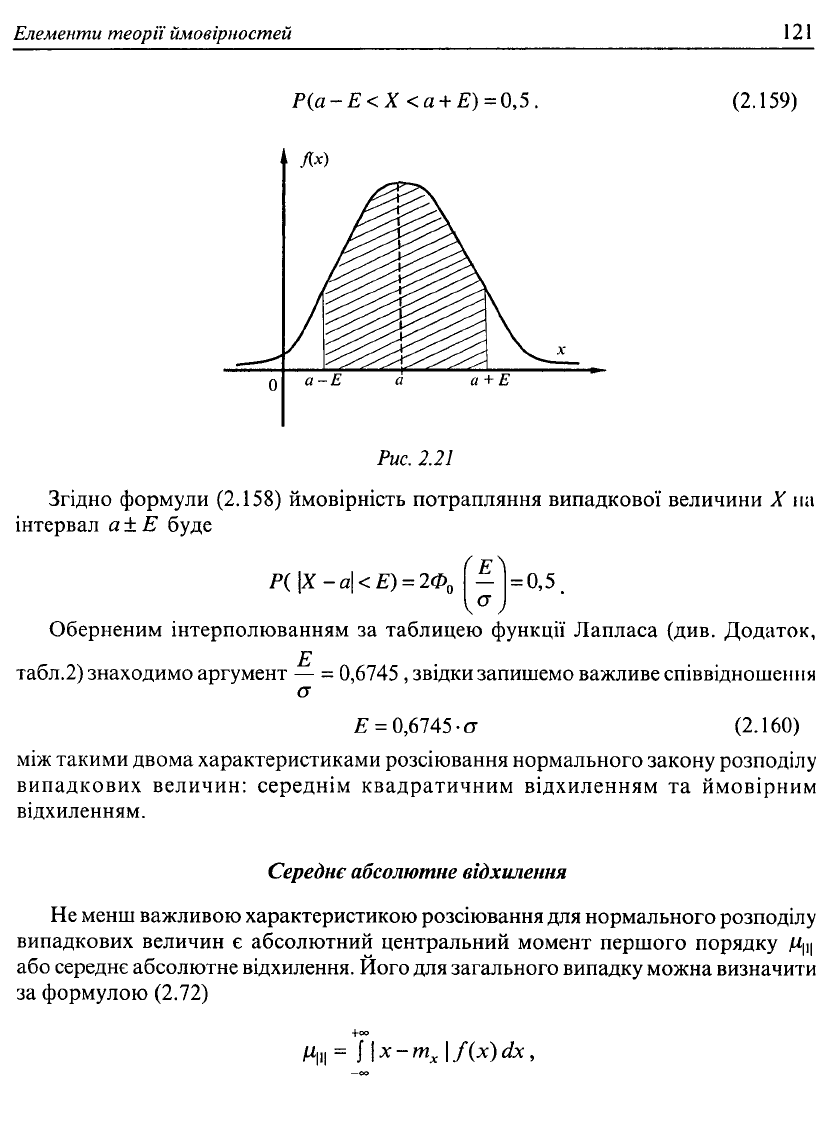
Р(а -Е<Х<а + Е) = 0,5, (2.159)

+ Е

Рис.

2.21

Згідно формули (2.158) ймовірність потрапляння випадкової величини X на

інтервал а ± Е буде

Р( \Х -а\< Е) = 2Ф

= 0,5

Оберненим інтерполюванням за таблицею функції Лапласа (див. Додаток,

табл.2) знаходимо аргумент — = 0,6745 , звідки запишемо важливе співвідношення

Е = 0,6745 а

(2.160)

між такими двома характеристиками розсіювання нормального закону розподілу

випадкових величин: середнім квадратичним відхиленням та ймовірним

відхиленням.

Середнє абсолютне відхилення

Не менш важливою характеристикою розсіювання для нормального розподілу

випадкових величин є абсолютний центральний момент першого порядку

або середнє абсолютне відхилення. Його для загального випадку можна визначити

за формулою (2.72)

+оо

= !\х-т

I f(x)

dx,

Розділ II

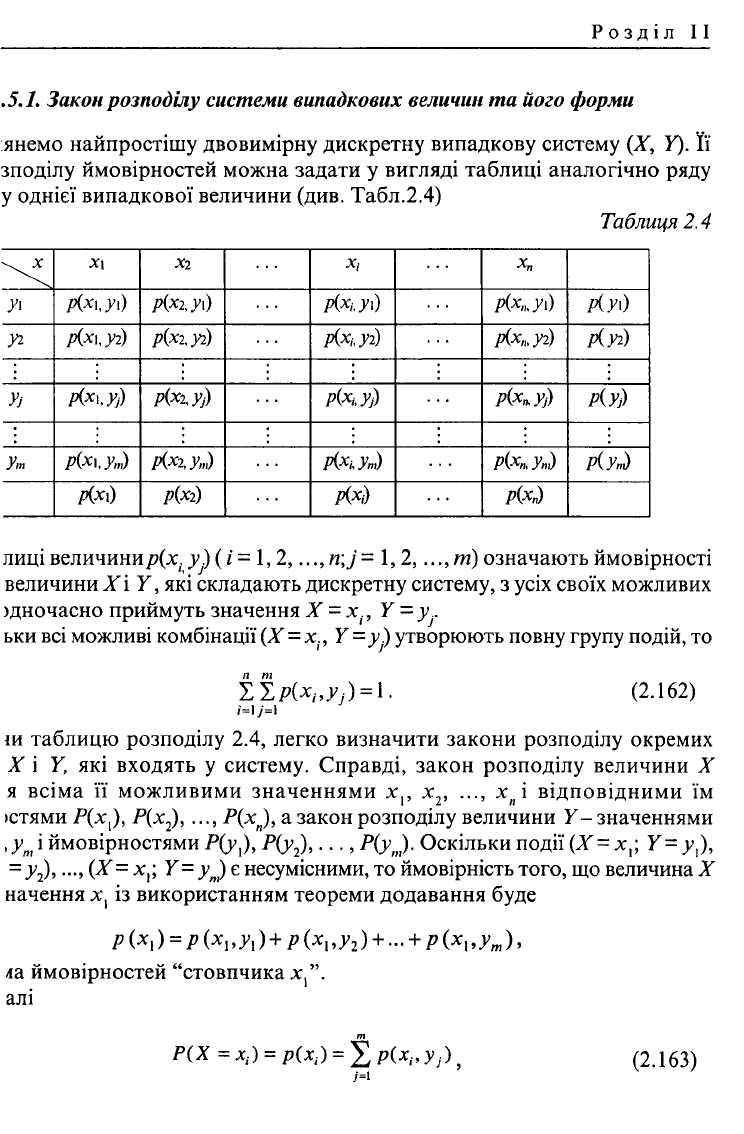
.5.1. Закон розподілу системи випадкових величин та його форми

янемо найпростішу двовимірну дискретну випадкову систему (X, У). Її

зподілу ймовірностей можна задати у вигляді таблиці аналогічно ряду

у однієї випадкової величини (див. Табл.2.4)

Таблиця 2.4

Х\ Хг

Xі

У\

Р(х\,у\)

Р(Х2,У\)

РІХі.уі) Р(Х„,У\)

РІУО

Уг

/Ххі,

уі) Р(Х2,У2)

ріх„уі)

Р(х

,уг)

РІУ2)

У]

РІХІУІ)

Р(Х2,У))

Р(Хі,У.і)

РІ

п, Уі)

РІ У])

Ут

РІх\,у

)

РІХ2,У

)

РІХиУт)

р(х„, у„)

РІУп)

Р(х і) Р(Х2) Р(Хі) р(х„)

лиці величинир{х. у^ (і = 1,2, ...,n;j= 1,2, ...,т) означають ймовірності

величини Xі Y, які складають дискретну систему, з усіх своїх можливих

щночасно приймуть значення X = х., Y = у .

ьки всі можливі комбінації (Х=х., Y=yутворюють повну групу подій, то

п т

llp(x

) = 1. (2.162)

i=\j=\

ш таблицю розподілу 2.4, легко визначити закони розподілу окремих

X і Y, які входять у систему. Справді, закон розподілу величини X

я всіма її можливими значеннями х,, х

, ..., х

і відповідними їм

істями Р(х

), Р(х

),..., Р(х

), а закон розподілу величини Y- значеннями

,у

і ймовірностями Р(у,), Р(у

),..., Р{у„). Оскільки події {X = х,; Г= j,),

= у

),..., {Х= х,; Y= у

) є несумісними, то ймовірність того, що величина X

начення х, із використанням теореми додавання буде

р(х

) = р(х

,у

) + р{х

,у

) + ... + р{х

,у

<а ймовірностей "стовпчика х,".

алі

Р(Х=х

) = р(х

) = %р(х

,у

)

;

(2.163)

Елементи теорії ймовірностей

123

P(Y = y

) = p(y

) = %p(x

(2.164)

Отже, закони розподілу окремих величин, які входять у систему, утворюються

сумами ймовірностей у відповідних рядках і стовпчиках.

Функцією розподілу системи (X, У) двох випадкових величин називається

ймовірність того, що компоненти системи одночасно приймуть значення X < х

та Y < у

F(х, у) = Р(Х <х, Y < у). (2.165)

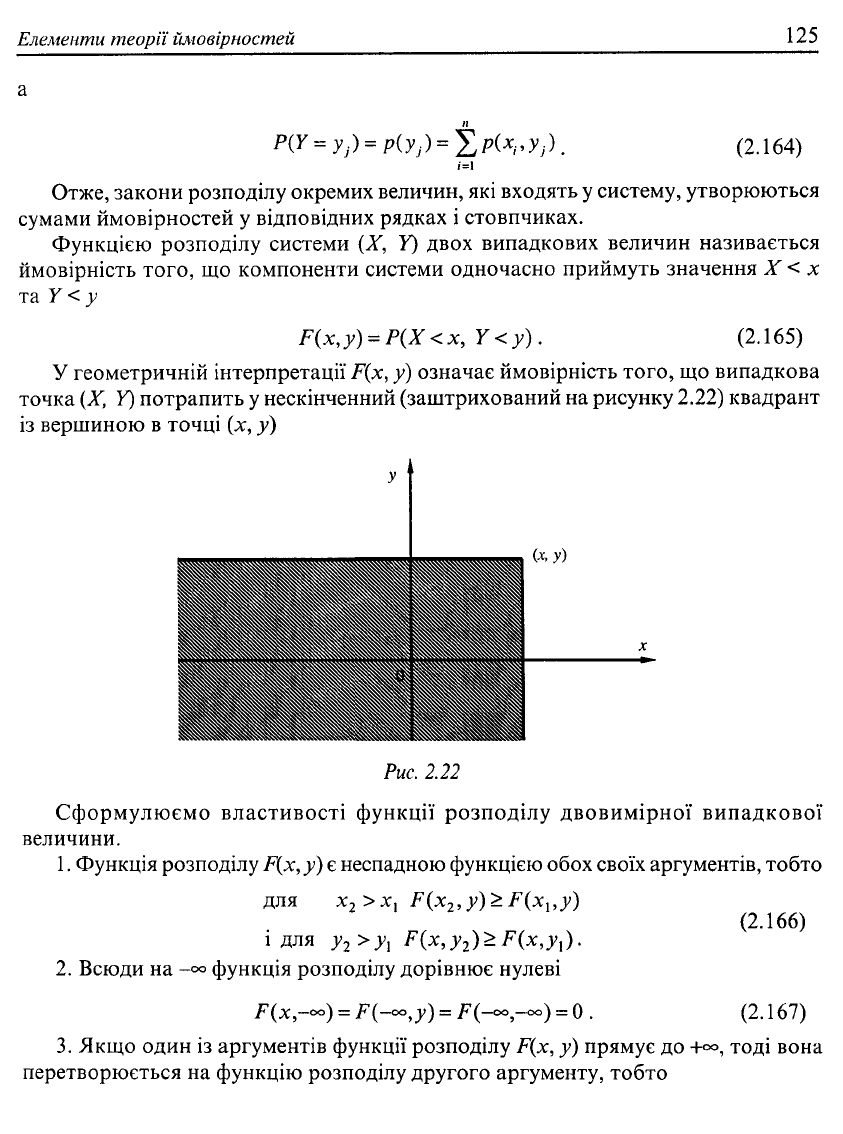
У геометричній інтерпретації F(x, у) означає ймовірність того, що випадкова

точка {X, Y) потрапить у нескінченний (заштрихований на рисунку 2.22) квадрант

із вершиною в точці (х, у)

Рис.

2.22

Сформулюємо властивості функції розподілу двовимірної випадкової

величини.

1. Функція розподілу F(x, у) є неспадною функцією обох своїх аргументів, тобто

для х

>х, F(x

,y)>F(x

,y)

(2.166)

і для У

>УІ F(x,y

)>F{x,y

2. Всюди на -оо функція розподілу дорівнює нулеві

F(x-оо) = F(-°°,y) = F(-оо-оо) = о . (2.167)

3. Якщо один із аргументів функції розподілу F(x, у) прямує до +оо, тоді вона

перетворюється на функцію розподілу другого аргументу, тобто

Розділ II

F(x,+°°) = F

(x), F(+*o,y) = F

(y). (2.168)

[кщо обидва аргументи прямують до то

F(+oo,+oo) = 1. (2.169)

праведливості всіх наведених властивостей легко переконатися, виходячи

:тричної інтерпретації функції F(x, у) (див. Рис. 2.22).

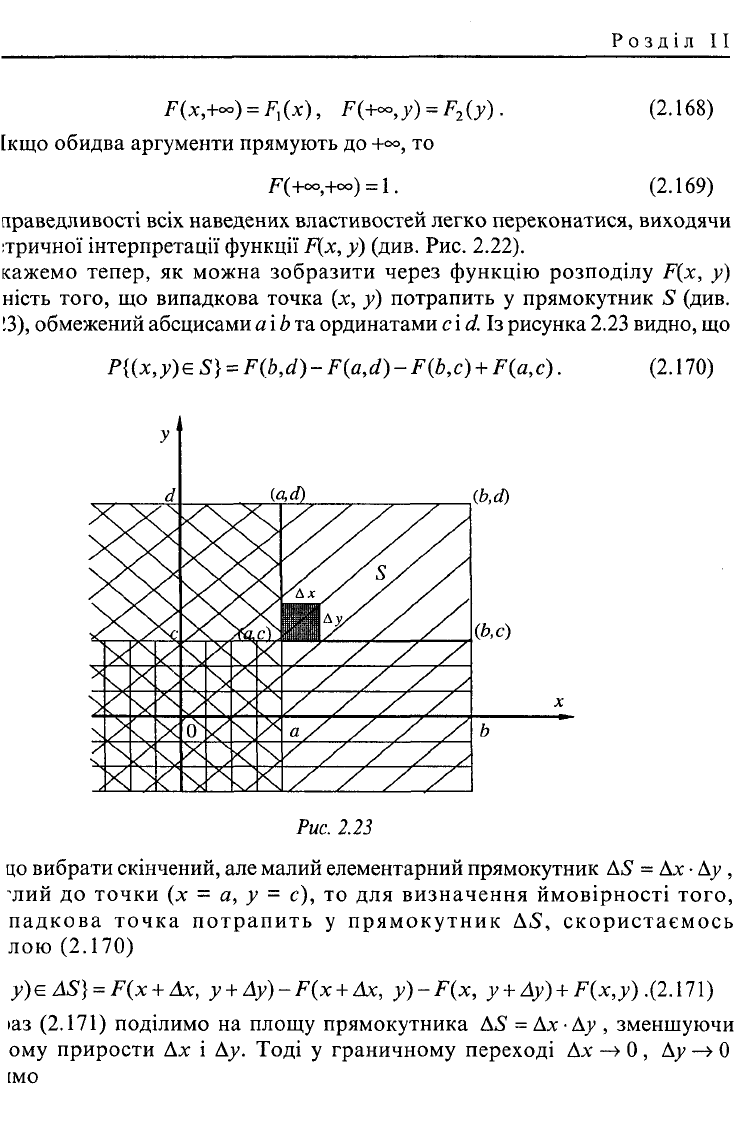
кажемо тепер, як можна зобразити через функцію розподілу F(x, у)

ність того, що випадкова точка (х, у) потрапить у прямокутник S (див.

!3), обмежений абсцисами а

b та ординатами СІЙ?, ІЗ рисунка 2.23 видно, що

Р{{х,у)е 5} = F(b,d) - F{a,d) - F(b,c) + F(a,c). (2.170)

Рис.

2.23

цо вибрати скінчений, але малий елементарний прямокутник AS = Ах

•

Ау ,

чіий до точки (х = а, у = с), то для визначення ймовірності того,

падкова точка потрапить у прямокутник AS, скористаємось

лою (2.170)

у)є AS} = F(x + Ax, y + Ay)-F(x + Ax, y)-F(x, y + Ay) + F{x,y).{2.\l\)

іаз (2.171) поділимо на площу прямокутника AS - Ах-Ay , зменшуючи

ому прирости Дх і Ау. Тоді у граничному переході Ах

—>

0 , Ау

—>

їмо

Елементи теорії ймовірностей 125

125

f^y) =

Ку(х,У)

•

(2.173)

Ит

/>{(*,У) є AS} _

Ах->о AxAv

(2.172)

F(x

+ Ax,

Ay)-F(x

+ Ax,

y)-F(x, y

+ Ay) +

F(x,y)

dx->o Ax Ay

Ay-> 0

Якщо функція розподілу F{x,y) буде

не

лише неперервною, а

диференційованою,

тоді права частина виразу (2.172) означатиме другу мішану часткову похідну (функції

F{x,y), яку позначимо

через/{х,у),

тобто

F(x,y)

дх ду

Функція/(х,у) називається густиною розподілу ймовірностей системи (.V,)')

двох неперервних випадкових величин. Вона описує так звану поверхню розподілу

—

f (х,у), яка за своїм змістом подібна до кривої функції густини розподілу

одновимірної величини.

Наведемо властивості функції густини розподілу/(х,у).

1. Густина розподілу системи (X,

У)

двох випадкових величин є функцією

невід'ємною

f(x,y)>0. (2.174)

2. Подвійний інтеграл від функції густини розподілу по нескінченій області

дорівнює одиниці

J ]f(x,y)dxdy = \. (2.175)

—оо —оо

Для однієї неперервної випадкової величини ми вводили поняття елемента

ймовірності (див. §2.3). Так само для системи двох неперервних випадкових

величин (X, Y) елементом ймовірності називається вираз

f(x,y)dxdy, (2.176)

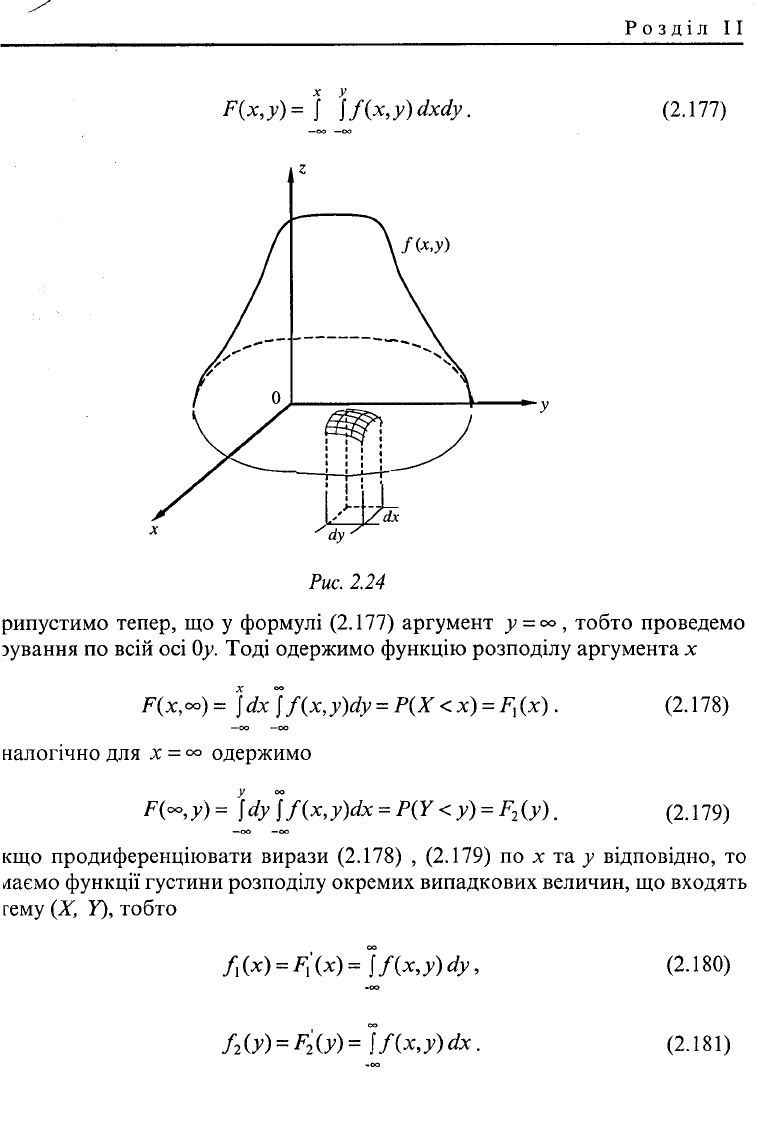
який у геометричній інтерпретації означає ймовірність того, що випадкова точка

потрапляє в елементарний прямокутник dS = dx-dy, а за величиною дорівнює

об'єму прямокутного паралелепіпеда з основою dS і обмеженого зверху поверхнею

=Лх,у) (див. Рис. 2.24).

Користуючись поняттям елемента ймовірності, ми можемо для інтегральної

функції розподілу двовимірної неперервної випадкової величини записати таке

співвідношення:

Розділ III

F{x,y)=] ]f(x,y)dxdy. (2.177)

Рис.

2.24

рипустимо тепер, що у формулі (2.177) аргумент y = тобто проведемо

зування по всій осі Оу. Тоді одержимо функцію розподілу аргумента л:

F(x,oo)= ]dx]f(x,y)dy = P{X<x) = F

{x). (2.178)

—оо —оо

налогічно для х-°° одержимо

F(oo,y)= ]dy]f{x,y)dx = P{Y<y) = F

{y). (2.179)

кщо продиференціювати вирази (2.178) , (2.179) по х та у відповідно, то

лаємо функції густини розподілу окремих випадкових величин, що входять

гему {X, Y), тобто

MX) = F;(X) = ]f{x,y)dy, (2.180)

fi{y)

= F

{y)=]f{x,y)dx. (2.181)

Елементи теорії ймовірностей

129

Наведемо приклади.

Приклад 1. Задано закони розподілу кількості попадань у мішень двох

стрільців

X 1 2

У 1

1 2.

Рі

0,1

0,3

0,6

Рі

0,2

0,3 0,5

Потрібно знайти закон розподілу кількості сумісних попадань.

Розв'язання. Складаємо ряд розподілу системи випадкових величіні (Л", )')

сумарної кількості попадань, для чого обчислимо такі ймовірності:

Ри

=р(Х -1;

0,1

-0,2 = 0,02 ;

= Р(Х =

F = 2)1

або Р(Х =

Y =

= 0,1-0,3 + 0,3-0,2 = 0,09

і т.д.

(XY)

3 4 5 6

Ри

0,02

0,09 0,26 0,33 0,30

Приклад 2. Знайти функцію густини f[x, у) розподілу системи (X, У), якщо

відома функція розподілу

F(x,j>) = sinx-siny

'о<х<-; 0<у<-

Розв'язання. За означенням функції густини як диференціальної функції

запишемо

дхду

Знайдемо часткову похідну по х від інтегральної функції

дх

•

cosx-siny

і після цього отриманий результат продиференціюємо по у

дхду

•

cosx- cosy.

Отриманий вираз і буде шуканою функцією густини, тобто

/(х,у) = cosx

•

cos у

0<х<— ; 0<у<-

2 2

Розділ III

.5.2. Умовні закони розподілу. Залежні і незалежні випадкові величини

ункті 2.5.1 ми бачили, що знаючи закон розподілу двовимірної випадкової

іни, легко знайти і закони розподілу окремих величин системи (X, Y). Однак,

зання оберненої задачі, тобто за відомими законами розподілів компонент

і закон розподілу системи, в загальному випадку не завжди є можливим,

розв'язання необхідно, крім законів розподілу компонент, знайти ще і

гість між ними, яку можна характеризувати за допомогою так званих

их законів розподілів.

овним законом розподілу випадкової величини X, що входить в систему

називається її закон розподілу, знайдений при умові, що друга величина Y

яла певне стале значення у, або навпаки.

овні закони розподілу можна задавати в різній формі. Так, наприклад, для

:тних випадкових величин системи (X, Y) найпростіше вони задаються

я розподілів (див. Табл. 2.5, 2.6).

Таблиця 2.5

Xi Х\

Х2

Х/1

РІх,! у)

р(хі/ у)

pixilyj)

p{xj у)

для

Y =

у j

Таблиця 2.6

Уі

У і У 2

Уп,

РІУ]І

*д

p(y\І

Хі)

р(у

І X/)

p(yj

Хі)

для X = х,.

габлицях 2.5 і 2.6 умовні ймовірності р(х.І у^ і piyjl х) можна зобразити

Зезумовні

ймовірностір{х),р(у

}

) ір(х

ур

за допомогою таких формул (за

лею виразів (2.23) § 2.1):

P(x

) =

P(yjlx,) =

P(Xi,yj)

p(.Vj) '

P(x„yj)

Pix,)

їй цьому завжди повинні виконуватись рівності

ip(x

lyj)

= l,

і=і

lp(y

)

= l.

7=1

(2.182)

(2.183)

(2.184)

(2.185)

Елементи теорії ймовірностей

131

Справді, подія, яка полягає в тому, що при заданому значенні однієї випадкової

величини системи (X, Y) друга з них обов'язково прийме одне з можливих своїх

значень, є достовірною.

Для неперервних випадкових величин системи {X, Y) умовні закони розподілу

переважно задаються функціями густини розподілу і їх позначають f(x/у), Jiy

х).

Між ними і безумовними функціями густини розподілу fix, y),f\ix),f

iy) існують

певні співвідношення. Щоб знайти їх, скористаємося поняттям елемента

ймовірності fix, y)dxdy.

Розглянемо достатньо малий, прилеглий до точки іх,у) елементарний

прямокутник площа якого дорівнює dS зі сторонами dx і dy . Ймовірній і.

потрапляння в цей прямокутник - елемент ймовірності fix, y)dxdy - дорівнює

ймовірності одночасного потрапляння випадкової точки (х, у) в елементарні смути

dx і dy (див. Рис. 2.25), тобто

f(x,y)dxdy = p{ix,y)edS} = P{ix<X<x + dx),iy<Y<y + dy)). (2.186)

dyj

Рис.

2.25

Але ймовірність добутку двох подій, вказаних у фігурних дужках виразу

(2.186), дорівнює ймовірності однієї з них, помноженій на умовну імовірність

другої, обчисленій при умові, що перша подія вже відбулася. У граничному

випадку для dx

—>

0 подія (х < X < х + dx) переходить у подію (X = х). Отже,

застосовуючи згадане правило множення, замість виразу (2.186) можна записа ти

f{x,y)dxdy = f

(x)dxf(y Іx)dy,

або

f(x,y) = Mx)f(y/x).

(2.187)

Розділ III

алогічно для граничного випадку dy

—>

f(x,y) =

My)f(x/y).

(2.188)

ким чином, густина розподілу системи двох (X,Y) випадкових величин

:ює густині розподілу однієї з них, помноженій на умовну густину розподілу

величини, обчислену при умові, що перша з них набула задане значення. Це

по називають теоремою множення законів розподілів,

формул (2.187) і (2.188) легко знайти вирази для умовної густини розподілу

зностей Упри заданому значенні

лг,

а також умовну густину розподілу ймо-

;тей X при заданому значенні у, тобто

= (2.189)

,, , ч /(*. у)

<2Л90)

риймаючи до уваги вирази (2.180) і (2.181), отримаємо

Ду/х)

= /

(Х,У)

, (2-191)

\f{x,y)dy

ДхІу)= /

(Х

У)

. (2.192)

\f{x,y)dx

—©о

іким чином, кожному можливому значенню однієї величини системи

(X,Y)

відповідати свій умовний закон розподілу іншої величини. Залежність між

іинами саме і проявляється в зміні умовного закону розподілу, наприклад,

іини У при переході від одного значення X до іншого. Тому цю залежність

а виявити шляхом порівняння умовних законів розподілів із відповідним

ювним. А саме, випадкова величина Уназивається залежною від випадкової

шни X, якщо закон розподілу величини У залежить від того, якого значення

іа величина X, тобто умовний закон розподілу величини У відрізняється від

ювного. Якщо умовні закони розподілу величини У залишаються незмінними

;сіх значень величини X, тоді ці величини будуть незалежними і в цьому

зку матимемо для дискретних випадкових величин

P(y

) = p(y

) (2.193)

неперервних