Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань

Подождите немного. Документ загружается.

Елементи теорії ймовірностей

111

2а

(2.125)

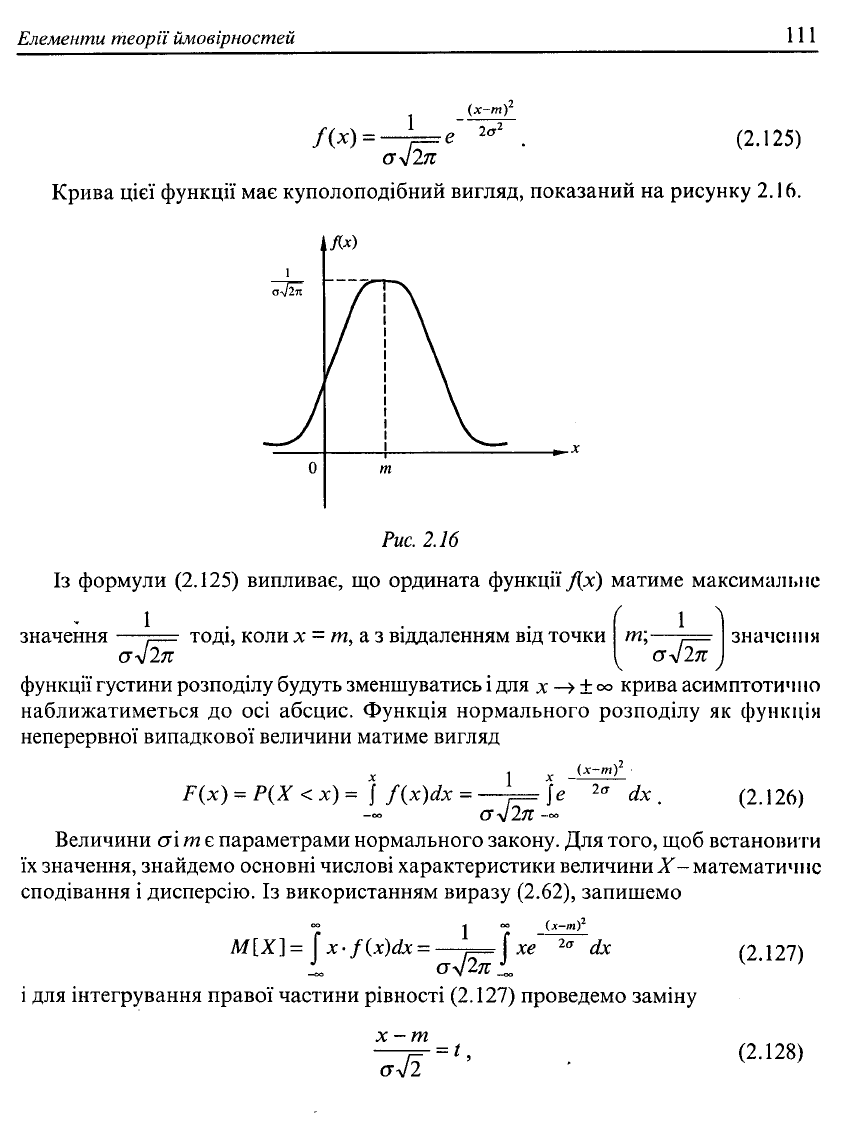
Крива цієї функції має куполоподібний вигляд, показаний на рисунку 2.16.

\Ях)

Рис.

2.16

Із формули (2.125) випливає, що ордината функції f[x) матиме максимальне

значення

<7лі2Я

тоді, коли х = т, аз віддаленням від точки

т;

СГлІ2п

значення

функції густини розподілу будуть зменшуватись і для х

—>

оо

крива асимптотично

наближатиметься до осі абсцис. Функція нормального розподілу як функція

неперервної випадкової величини матиме вигляд

F(x) = Р(Х < х) = / f(x)dx =

(x-mf

іе

2а

(2.126)

СГу/іЯ

Величини crime параметрами нормального закону. Для того, щоб встановити

їх значення, знайдемо основні числові характеристики величини X- математичне

сподівання і дисперсію. Із використанням виразу (2.62), запишемо

°° і « (х-т)

М[Х]= \x-f(x)dx = —==Г.

і osibtt

хе

2а

dx (2.127)

і для інтегрування правої частини рівності (2.127) проведемо заміну

• т

оЛ

= t.

(2.128)

Розділ II

>го визначимо х = o4l t + т і dx = о>І2 dt. Межі інтегрування залишаться

самими. Після підстановки виразів для х та dx у праву частину рівності

одержимо

і F? °°

М[Х]= z. \(a4l t +т)е~'

dt,

у]л сгл/2

,,,,,, <Тл/2 7 _,2 w 7 _,2 ,

М[ЛГ] = —J7e ' dt + -j= fe ' dt. (2.129)

V7T л/Я

іший доданок виразу (2.129) є рівним нулеві, оскільки це є інтеграл від

ої функції на нескінченому симетричному відрізку.

тим доданком є інтеграл Ейлера-Пуассона, який дорівнює . Отже,

ь (2.129) перепишемо так:

M[X] = -^LJtz =т.

ЛІЛ

бачимо, параметр т є математичним сподіванням випадкової величини X.

одальшому ми будемо часто використовувати заміну (2.128). Із цього приводу

/важити, що перехід від нормально розподіленої випадкової величини Хдо

ни X-т

, називається її центруванням. Перехід же від величини Х-т

до t

'мулою (2.128) називається нормуванням. Необхідність у проведені над

іною X цих двох операцій, крім спрощення записів при доведенні різних

л і співвідношень, обумовлюється ще деякими обставинами,

перше, нормально розподілена випадкова величина X у результаті багатьох

ережень або вимірювань може приймати великі числові значення (наприклад,

тати вимірювання кута). Це приводить до незручностей при дослідженні

випадкових величин і проведенні над ними різних математичних операцій.

/никнути цього, переходять до центрованої величини X = X -т

. Ці

ення, очевидно, теж підпорядковуватимуться нормальному закону, а числові

ня їх будуть зображатися малими числами через те, що в переважній більшості

ків можливі значення випадкової величини X мало відрізняються від

атичного сподівання т

і-друге, відхилення X - т

будуть мати розмірність величини X. Але для

;ння загальних властивостей нормального та інших законів розподілу, які

:ежали б від фізичної природи самої величини X , бажано оперувати з

імірною величиною. Для цього відхилення X-т

ділять на &

. У результаті

ують безрозмірну випадкову величину

Елементи теорії ймовірностей 113

^ Х-т

Z = S (2.130)

зображену в долях середнього квадратичного відхилення. її називають

центрованою, нормованою і нормально розподіленою випадковою величиною з

математичним сподіванням

M[Z} = -M[{X-m

)] = 0 (2.131)

і середнім квадратичним відхиленням

a[Z] = 4D[Z]=^M[(x-m

)

]=:l. (2.132)

Приймаючи до уваги формули (2.130) - (2.132), функцію густини розподілу

(2.125) можна записати тепер в такому вигляді:

/(z) = -pL<T

, (2.133)

V 2л

або скорочено n(Z\ 0; 1). Цей запис означає, що випадкова величина Z розподілена

за нормальним законом з параметрами т = 0 і а- 1. Подібний запис застосовують

і для функції розподілу випадкової величини Z, а саме

F(z) = P(Z <z) = ]e~

dz = N(Z; 0,1). (2.134)

лі 2л

Очевидно, що випадкова величина t теж буде нормованою і нормально

розподіленою випадковою величиною з функціями розподілу і густини розподілу

F(t)^~'\e~'

dt, (2.135)

f{t)

= ^-

(2.136)

УІЛ

ВІДПОВІДНО.

Після цих зауважень знайдемо тепер дисперсію D[X\. Згідно формул (2.72) -

(2.79) запишемо

U'-m)

D[X]

=—= l(x-m)

dx. (2.137)

а л/2л —

Розділ II

демо змінну величину t за формулою (2.128). Тоді

dx - Сл/2 dt, (х - т)

= 2a

, (2.138)

інтегрування залишаються незмінними. Після підстановки виразів (2.138)

/ частину співвідношення (2.137) одержимо

2а

—т=^

jt е dt.

ЛІ 71

ггруючи отриманий вираз частинами із використанням формули

\и dv = uv - Jv du,

u = t, dv = te~' dt,

іємо

du = dt, v = fte ' dt -

•

2 '

D[X] =

2 a

-t-

+ - f e ' dt

2-00

D[X] = -

=-4n=a

. (2.139)

yJTT

<им чином, параметр є не що інше як середнє квадратичне відхилення

арт) випадкової величини X, яке характеризує форму кривої функції Дх)

и розподілу нормального закону. Максимальна ордината кривої —==

(ТЛ/2я:

яо пропорційна стандарту

сг.

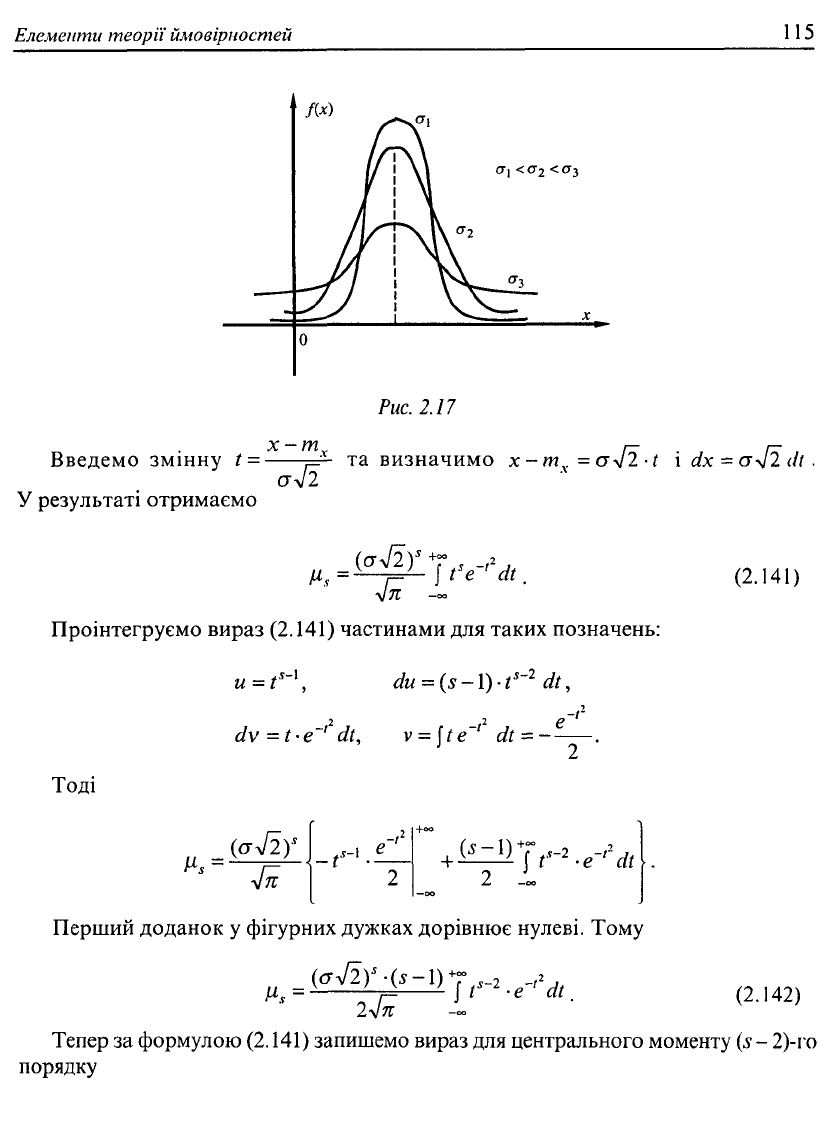
У зв'язку з тим, що площа, яка обмежена кривою

ії

Дх) і віссю абсцис, завжди дорівнює одиниці, то при збільшенні крива стає

плоскою, розтягується вздовж осі абсцис і навпаки (див. Рис. 2.17).

(менти нормального розподілу

римаємо тепер формули для визначення центральних моментів різних

ків. Згідно виразу (2.72) маємо

1 +ОС _(х-т.)

—J= I (х-т

у е

2а

dx. (2.140)

(Тл/2я -о»

Елементи теорії ймовірностей

115

fix)

\\ а

<о

<а

іг

— —

VS-.

Введемо змінну t =

У результаті отримаємо

х-т„

ст72

Рис. 2.77

та визначимо x-m

-a4l-t \dx-a4ldt.

/і, J ' dt.

V7T

Проінтегруємо вираз (2.141) частинами для таких позначень:

(2.141)

и = t

1-і

du = (s-l)-t

dt,

dv = t-e~'dt, v-Jte' dt---

Тоді

(су42 У

•JJг

-t'

-1 Є

Перший доданок у фігурних дужках дорівнює нулеві. Тому

(2.142)

Тепер за формулою (2.141) запишемо вираз для центрального моменту (я - 2)-го

порядку

Розділ II

(<7Л/2)

s-2

^—^-ir'-e-'dt. (2.143)

л/ТГ

зрівнюючи вирази (2.143) і (2.142) легко помітити, що вони відрізняються

на величину (я - І^о

, тобто

(2.144)

тримане просте рекурентне співвідношення дає можливість обчислювати

зальні моменти вищих порядків нормального розподілу через моменти

их порядків.

ак, наприклад, момент третього порядку

^з = (3 -1)

•

• fx

= 2а

•

і, =0 як момент першого порядку центрованої випадкової величини. Тому

= 0, а також, очевидно, і всі інші центральні моменти, непарного порядку

гь рівні нулеві.

бчислимо тепер декілька перших моментів парного порядку

=(2-1)-a

-fi

= а

НІ = (4-\)-ст

•

/л

= Зет

ІЛ

=(6-\)-<7

•

=\5А

•

агальна формула для момента 5-го порядку при парному s буде

M.,=(s-l)!!o

, (2.145)

імвол (5- 1)!! означає добуток всіх непарних чисел від

до s- 1.

)скільки з моментами ц і д, пов'язані числові характеристики асиметрія і

ес, то запишемо вирази для них

(2.146)

=~"--3 = ^ = 0. (2.147)

а а

Ймовірність потрапляння нормально розподіленої випадкової величини на

довільний інтервал. Функція Лапласа

Цля обчислення такої ймовірності (див. §2.3 формула 2.47), треба знати приріст

кції розподілу на цьому інтервалі, тобто

Р(а <Х <Р) = F(j3) - F(cc).

А'

= 0,

£4_

-3 =

Зет

СГ

ст

Елементи теорії ймовірностей

117

Оскільки F(x) - функція нормального розподілу, то наведену рівність

перепишемо

Р(а<Х < /3) = —г=\

е 2

(2.148)

Введемо випадкову змінну Z за формулою (2.130), у результаті чого отримаємо

1 -іі

Р(а<Х<і3) = -j= J е

у/2Л д-т

(2.149)

Розглянемо таку функцію розподілу:

* I

-—

F (*) = -= \е

dz. (2.150)

л/2тг

Невласний інтеграл правої частини формули (2.150) не можна зобразити через

елементарні функції і він є подібним до так званого інтегралу ймо-

вірностей або функції Лапласа

0(x) = -^']e-'

dt, (2.151)

лі

1 ^

Фо(*) = -г=/е

2dz

- (2.152)

V 2л о

Наведені функції (2.151), (2.152) є протабульовані і для них складено таблиці

з метою полегшення обчислень для практичних розрахунків. Якою з цих функцій

користуватися - це справа користувача. У більшості практичних обчислень у

геодезичних задачах використовують функцію, подану виразом (2.152) (див.

Додаток, табл.2).

Функція Лапласа (2.152) має такі властивості:

1. Ф

(0) = 0 , оскільки для х = 0, верхня і нижня межа інтегрування співпадають.

1 z

2. Ф

(+оо) =

—

через те, що для t = —=

2 л/2

^ / ч

т -t

J \ 4л \

(оо)= je ' dt = — = -.

хЛ о \1л 2- 2

Розділ II

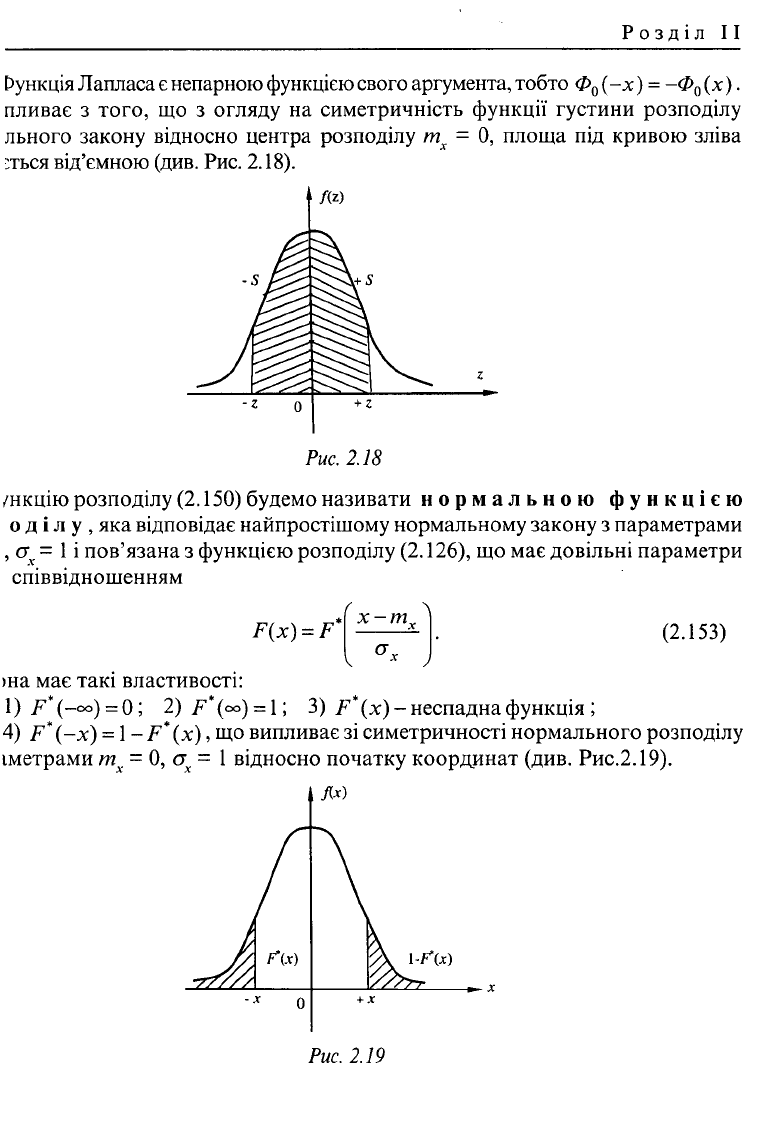
функція Лапласа є непарною функцією свого аргумента, тобто Ф

(-х) = -Ф

(х).

плнває з того, що з огляду на симетричність функції густини розподілу

льного закону відносно центра розподілу т

= 0, площа під кривою зліва

:ться від'ємною (див. Рис. 2.18).

Рис.

2.18

/нкцію розподілу (2.150) будемо називати нормальною функцією

о д і л у , яка відповідає найпростішому нормальному закону з параметрами

ст.

і пов'язана з функцією розподілу (2.126), що має довільні параметри

співвідношенням

F(x) = F

х-т

(2.153)

>на має такі властивості:

1) F*(-°°) = 0; 2)/'*(оо) = 1; 3) 7

*(х)-неспадна функція ;

(-х) =

(х), що випливає зі симетричності нормального розподілу

іметрами т. = 0, а = 1 відносно початку координат (див. Рис.2.19).

Рис.

2.19

Елементи теорії ймовірностей 119

Між функцією F*(x) і функцією Лапласа Ф

(х) існує очевидний зв'язок

F'(x) =

O,5

+ 0

(x), (2.154)

оскільки завжди J/(х)dx = \,& його половина J/(х)dx = 0,5 .

—оо ' —оо

Ймовірність потрапляння нормально розподіленої випадкової величини X на

інтервал від а до Д, де а і /3 - ліва та права межі інтервалу на числовій осі Ох

відповідно, обчислюють за формулою

/3-т

Р(а<Х <р) =

~Фп

а-т,

та використовують таблицю для функції Лапласа.

Якщо один, або обидва аргументи z, =

a -ra

і z

р-т

(2.155)

функції Лапласа

а " а

(г) будуть від'ємними, то для цих випадків необхідно приймати до уваги третю

її властивість 0

(-z) =

-Ф

(z).

Запишемо це

P(-z, <Z<Z

) = 0

)-0

(-z,) = Ф

) + Ф

(z,), (2.156)

P(-z

< Z < -z

) =

(~z

)

- Ф

(-z,) = -Ф

) + Ф

(z,), (2.157)

або

P(-z, < Z < -z

)- 0q(Z\)-0q(Z

) .

Ймовірність потрапляння нормально розподіленої випадкової величини на

інтервал, симетричний відносно центра розподілу

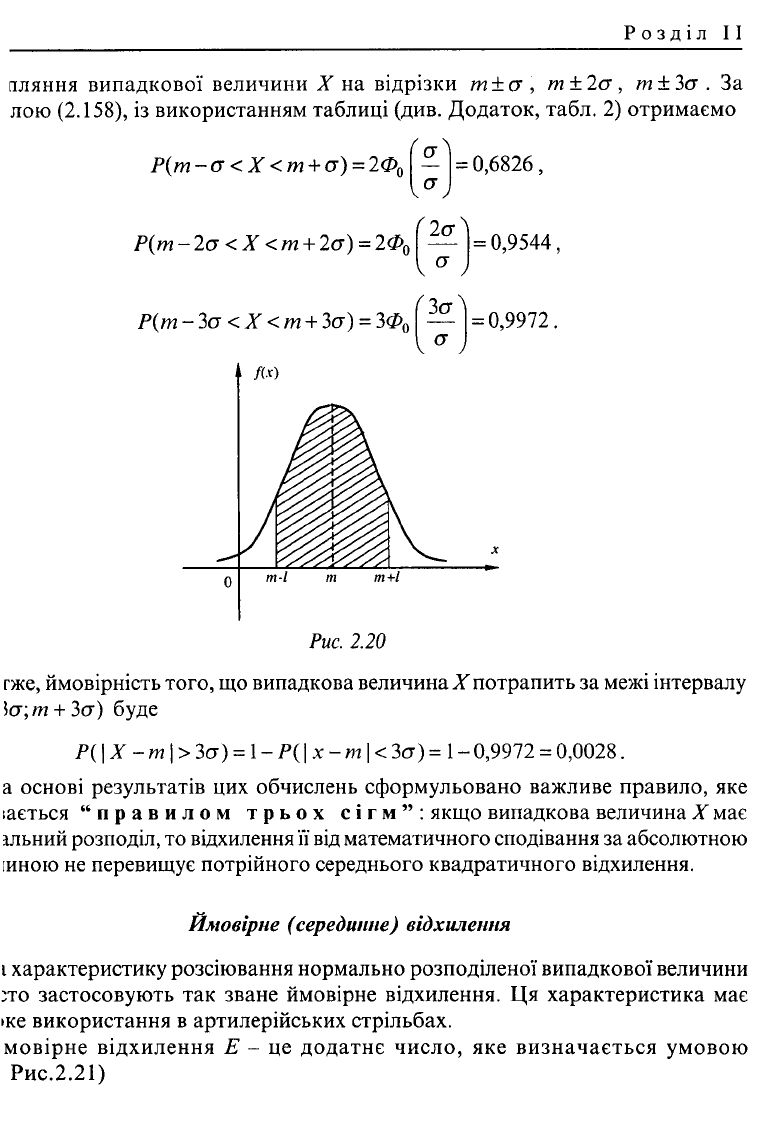
Зазначена задача часто зустрічається в практичних розрахунках. Розглянемо

інтервал довжиною 21 (див. Рис.2.20). Обчислимо ймовірність потрапляння на

цей інтервал нормально розподіленої випадкової величини, скориставшись

формулою (2.155)

Р{т-І <Х <т +

m + 1-m^

-Ф,

-Фл

сг

ґ і \

•Ф,

т-І-т

= 2Ф

(2.158)

А тепер розв'яжемо таку задачу: відкладемо відрізки довжиною сгвід центра

розподілу праворуч і ліворуч тричі послідовно. Обчислимо ймовірності

Розділ II

пляння випадкової величини X на відрізки т±<у , т±2о, т±3а . За

лою (2.158), із використанням таблиці (див. Додаток, табл. 2) отримаємо

Р(т -

сг

< X < т + с) = 2Ф

= 0,6826,

Р(т-2а<Х<т + 2а) = 2Ф

Р(т -

Зет

< X < т + Зет) = ЗФ

2а

v у

= 0,9544,

•

0,9912.

/(•V)

—

К •

т -1 т т+1

Рис.

2.20

гже, ймовірність того, що випадкова величина X потрапить за межі інтервалу

іа;т + За) буде

Р(\ X - т |> Зет) = \-Р{\х-т\<Зо) = 1-0,9972 = 0,0028.

а основі результатів цих обчислень сформульовано важливе правило, яке

іається "правилом трьох сігм": якщо випадкова величина X має

ільний розподіл, то відхилення її від математичного сподівання за абсолютною

!иною не перевищує потрійного середнього квадратичного відхилення.

Ймовірне (серединне) відхилення

і характеристику розсіювання нормально розподіленої випадкової величини

;то застосовують так зване ймовірне відхилення. Ця характеристика має

же використання в артилерійських стрільбах.

мовірне відхилення Е - це додатне число, яке визначається умовою

Рис.2.21)