Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань
Подождите немного. Документ загружается.


Елементи теорії ймовірностей
Центрування випадкової величини X рівносильно переносу поча тку коор.ііні.і
і
числової осі в середню центральну точку, абсциса якої дорівнює ма гема
і
нчиом\
сподіванню т .
х
о
Центрована випадкова величина X має ту властивість, що матемаіпчмг
сподівання її завжди дорівнює нулеві.
Справді
М[Х} = М[(Х-т
х
)} = £(х,--т
х
)
Рі
= ±х
іРі
-т
х
І
Рі
=т
х
-т=( )• (2.(>9)
/=і ,=і І=І
Аналогічно для неперервної випадкової величини
М[Х]= ](x-m
x
)f(x)dx = ] xf{x)dx-m
x
]f(x)dx = m
x
-m
x
=Q. (2.70)
—оо —оо — ©о
Моменти центрованої випадкової величини називаються ц е н т р а л
і>
її її м п .
тобто центральним моментом 5-го порядку центрованої вішадкоиоі
величини X називається математичне сподівання 5-го степеня цієї величніш
ti
s
[h = M[X] = t(x
i
-m
x
y
Pi
, (2.71)
(=і
fi
s
[h
=
M[X]= ](x-m
x
yf(x)dx. (2.72)
Між початковими і центральними моментами існують співвідношення, які
можна довести, користуючись формулами (2.61), (2.62), (2.65), (2.66), (2.69), (2.70)
jU, =0, (2.7.1)
ц
2
=v
2
-v\ =v
2
-т
2
х
, (2.74)
/л
}
= v
3
-3v
2
v, + 2v
2
= v
3
-3v
2
m
x
+2m
2
x
, (2.75)
Ц4 =v
4
-4v
3
v, + 6v
2
v,
2
— 3Vj
4
-v
4
-4v
3
m
x
+6v
2
m
2
-3m*. (2.76)
Доведемо, наприклад, формули (2.74) і (2.75) для дискретної випадкової
величини. Для центрального моменту другого порядку запишемо
V
2
=M[(X-m
x
)
2
) =
= £(*,- ~т
х
)
2
Рі
= І(х
2
-2т
х
х
і
+т\)р
і
= fx
2
Pi
-2m
x
tx
iPi
+m
2
x
t
Pi
=
і=1 /=і /=г /=1 і=1
звідки д
2
= v
2
-m
= v
2
-2т
г
х
+т
х
,
2

Розділ II
Для центрального моменту третього порядку одержимо
^=M[(X-mJ] = t(х, - m
3
fp
t
= £(xf - 3m
x
x
2
+ 3mix, -m\)
Pi
=
1=1 /=1
= £ хІРі - зm
x
£ xfp, + 3w
2
£ x
iPi
-ml £
Pi
,
/=1 i=i i=i i=i
[ЦСИ
=v
3
-3m
x
v
2
+ 3m
2
v, -mj,
)
03
= V/
3~
3v/
2
W
;t+
2
™*-
Для довільного порядку центральні та початкові моменти пов'язані
ввідношеннями
т . —і
lL
m
= S(-1)'-C -х ,
т
= 0,1,2,...,
і=0
, /я!
m
/! (m-/)l
Існує ще одна група числових характеристик випадкової величини, яка
іактеризує міру розсіювання окремих її значень навколо центра, або тісноту
пування можливих значень випадкової величини навколо центра. Головною
>актеристикою цієї групи є центральний момент другого порядку , який
іивається дисперсією і позначається D[X] або D
x
. Дисперсія означає міру
ісіювання. Згідно означення, дисперсією випадкової величини X
іивається математичне сподівання квадрату відповідної центрованої величини
D[X]=M[(X-m
x
)
2
]. (2.77)
Для обчислення дисперсії користуються такими формулами:
D[x]
= t(x
i
-m
x
)
2
p
i
(2.78)
і=і
[ дискретної випадкової величини X і
D[x] = J(x-m
x
)
2
f(x)dx (2.79)
—оо
і неперервної випадкової величини X.
Іноді для обчислення дисперсії зручно користуватися співвідношенням (2.74)
>
виразом

Елементи теорії ймовірностей 93
£(*,.-т
х
)
2
р, = txfPj-(t*iPi)
2
. (2.80)
/=і /=і і=і
Дисперсія D[X] має розмірність квадрату розмірності випадкоінн
величини X. Але практично за міру розсіювання краще брати величину,
розмірність якої дорівнює розмірності самої випадкової величини. Тому,
вводиться величина
o
x
=o[X] = ^D[X], (2.81)
яка називається стандартом (флюктуацією), або середнім
квадратичним відхиленням.
Центральний момент третього порядку випадкової величини X характерн ої
асиметричність кривої функції густини розподілу f(x) відносно ордина і н,
проведеної в точці з абсцисою, що дорівнює математичному сподіванню . Якщо
розподіл є симетричним відносно математичного сподівання, тоді всі момспіи
непарного порядку (якщо вони існують) дорівнюють нулеві, тому що н сумі
кожному додатньому доданку буде відповідати такий же від'ємний.
Отже, за характеристику асиметрії беруть найпростіший момент непарного
порядку, а саме центральний момент третього порядку, оскільки централі.пніі
момент першого порядку згідно виразу (2.69) завжди дорівнює нулеві.
Центральний момент 3-го порядку М
}
має розмірність, що дорівнює кубу
розмірності випадкової величини. Для того, щоб одержати безрозмірну
характеристику, вводять величину
4c=-f. (2.82)
о
х
яку називають "коефіцієнтом асиметрії" або просто "асимет-
рією", або "скошеністю".
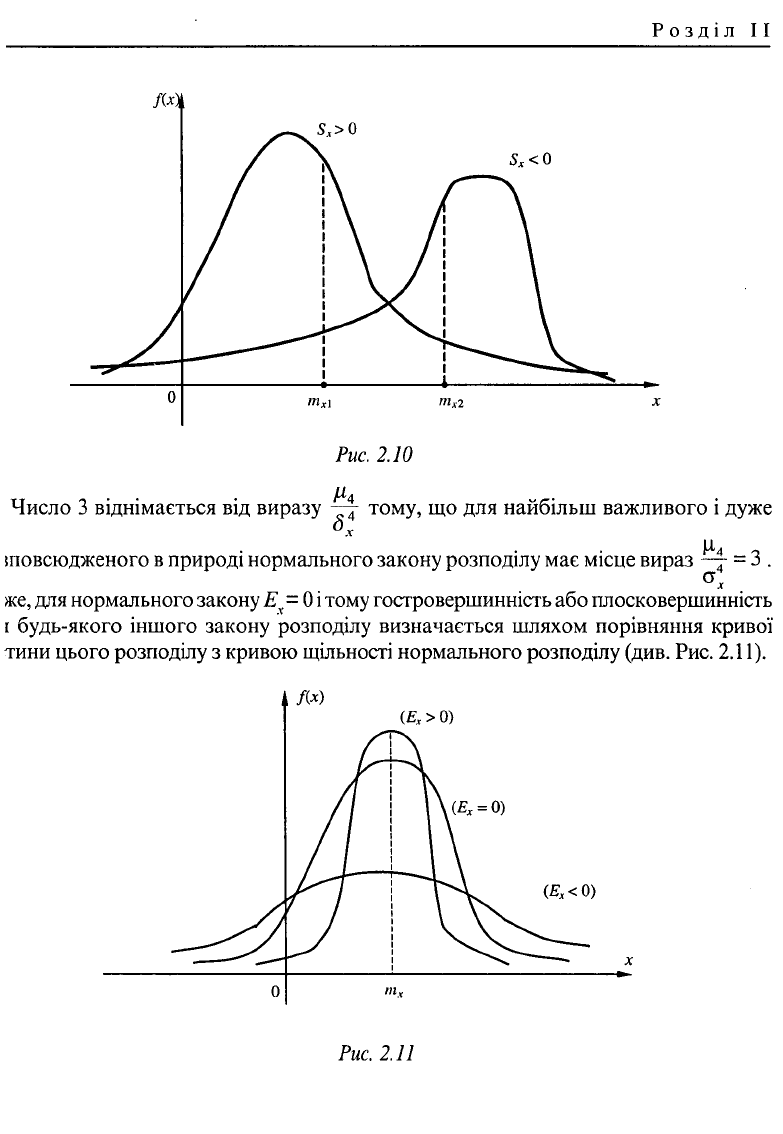
Коефіцієнт асиметрії А
х
> 0, коли довша частина кривої функції/^ лежить
праворуч від ординати точки з абсцисою т і А
х
< 0 - у протилежному випадку
(див. Рис. 2.10).
Центральний момент 4-го порядку характеризує гостровершинність або
плосковершинність кривої функції густини розподілу. Ці властивості описую ться
за допомогою так званого ексцесу, який позначають Е
х
. Ексцесом випадкової
величини називається величина
Розділ II
Число 3 віднімається від виразу —j тому, що для найбільш важливого і дуже
х
о
іповсюдженого в природі нормального закону розподілу має місце вираз -7 = 3.
же,
для нормального закону
JE'
v
= 0 і
тому гостровершинність або плосковершинність
і будь-якого іншого закону розподілу визначається шляхом порівняння кривої
тини цього розподілу з кривою щільності нормального розподілу (див. Рис. 2.11).
Рис.
2.11

Елементи теорії ймовірностей
95
2.3.5. Властивості головних числових характеристик.
Теореми про числові характеристики
При обчисленні числових характеристик випадкових величин доцілі.но
використовувати ряд теорем, які дають можливість досить просто визначні п мі
характеристики, а в деяких випадках і характеристики функцій випадкошіх
аргументів.
Знання цих теорем дозволяє значно спростити розв'язання баїаи.ок
практичних і теоретичних задач теорії ймовірностей.
Теореми про математичне сподівання
Теорема 1. Математичне сподівання сталої величини С дорівнює самій
цій величині
М[С\ = С. (2.8-1)
Сталу величину С можна вважати за дискретну випадкову величину, яка
приймає лише одне можливе своє значення Сз ймовірністю, такою, що доріїнпог
одиниці. Отже, М[С]= С • 1= С.
Теорема 2. Математичне сподівання добутку сталої величини на
випадкову дорівнює добутку сталої
величини
на математичне сподівання випадкової
величини
М[СХ]= СМ[Х\. (2.85)
Для дискретних випадкових величин можна записати такий вираз для
математичного сподівання:
М[СХ] = І CXjPi = СІх
іРі
= СМ[Х],
/=і і=і
а для неперервних випадкових величин відповідно такий вираз:
М[СХ] = J Cxf (x)dx = С Jxf(x)dx = СМ[Х].
Отже, сталу величину можна виносити за знак математичного сподівання.
Теорема 3. Математичне сподівання суми декількох випадкових величин
дорівнює сумі математичних сподівань цих величин
М[?
І
Х
І
] = £М[Х
І
]. (2.86)
і=І /=і

Розділ II
Доведемо теорему для випадку суми двох дискретних випадкових величин X
, тобто
М[(Х + У)] = М[Х] + M[Y\. (2.87)
Для цього припустимо, що кожна з величин має відповідний ряд розподілу
х
г
•
• •
X
л У. Уг
.
. •
у
т
У)
Р\
Рг
Р,
У)
Р\
Рг
р
т
Тоді можливими значеннями суми X + Y будуть величини х,- +yj (/ = 1,«;
-\,т). Позначимо ймовірність окремого можливого значення суми х,- + yj
рез р...
Згідно означення математичного сподівання маємо:
М[{Х + Y)] = І(х,. + у/)
Ри
= 2 Е(х, +
yj
)
Pij
= £ ЇХіРіі + 1IyjPo
ij i~\j=\ /=1у=1 /=1>І
п т т п
І=і
7
=і j=i І=і
(2.88)
Але XPij означає ймовірність того, що величина Xприйме значення х., тобто
у=1
Так само
1,р
и
=Р(Х = х
1
) = р
1
.
н
"Lp
lJ
=P{Y = y
j
) = p
J
.
і=і
(2.89)
(2.90)
Підставивши вирази (2.89) і (2.90) у співвідношення (2.88), одержимо
М[(Х + Y)] = £х
іРі
+ ly
jPj
= М[Х) + M[Y]
,=1 7=1
теорему доведено.
Для неперервних випадкових величин Хі У теорема доводиться аналогічно,
обто

Елементи теорії ймовірностей
97
M[(X + Y)] = l f{x
+
y)f(x,y)dxdy=\ j xf(x,y)dxdy
+
j \yf\x,y)dxdy
—оо — оо — оо
=
+
{V. (x)dx
+
+
\yf
2
(y)dy
=
MIX] + M[Y]*.
Методом індукції теорема узагальнюється на довільну кількість доданмн
Теорема 4. Математичне сподівання лінійної функції вигляду У - ч\ і
/>
дорівнює тій же функції від математичних сподівань аргументів.
Ця теорема є наслідком попередніх теорем 1,2 і 3.
М^щХі+Ь^М
де п - кількість аргументів.
1А
І
Х
І
і=і
+ М[Ь]
= ZM[a,X,] +
Ь
=
1 + !> •
(
2Ч1
>
і=І і=і
Теорема 5. Математичне сподівання добутку двох незалежнії \
випадкових величин дорівнює добутку їх математичних сподівань.
Ця теорема називається теоремою множення математичних споді на ні. і
записується так:
M[XY]= М[х]-M[Y]. (2.92)
Нехай величини Х\ У-дискретні та їх сумісний розподіл задається таблицею
розподілу ймовірностей р(х, у) = р(Х = х, Y = у). Тоді
M[XY]= Zxy.p(x,y)
(х,у)
У випадку незалежності випадкових величин можна записати
р(х,у) = р(х)-р(у)
і тоді
M[XY]= і[х-р(х)]-[ур(у)] = м[х]-м\у]
Аналогічно дане твердження можна довести і для неперервних випадкових
величин.
Для залежних випадкових величин теорему розглянемо в параграфі 2.5.
' Зміст функцій /j (х) та /
2
(у) подано в параграфі 2.5.

Розділ II
Теореми про дисперсію
Теорема 1. Дисперсія сталої величини дорівнює нулеві.
Доведення. Згідно означення дисперсії маємо
D[C] = М[(С - т
с
)
2
]
= М[(С - С)
2
]
= 0. (2.93)
Теорема 2. Дисперсія добутку сталої величини С на випадкову величину X
івнює добутку квадрата сталої величини на дисперсію випадкової
D[CX] = C
2
D[X]. (2.94)
Зважаючи на те, що сталу величину С можна виносити за знак математичного
дівання, маємо
СХ] = М[(СХ - М[СХ] )
2
] = М[(СХ - СМ[Х] )
2
] = С
2
М[(Х - М[Х} )
2
] = C
2
D[X].
Отже, сталу величину С можна виносити за знак дисперсії, підносячи її при
>му до квадрату.
Теорема 3. Дисперсія суми або різниці двох незалежних випадкових величин
нвнює сумі дисперсій цих величин
D[X ±Y] = D[X] +D[Y]. (2.95)
За формулою для обчислення дисперсії маємо
D[X±Y] = M[(X±Y)
2
]-[M(X±Y)]
2
. .
Розкривши дужки, використовуючи при цьому властивості математичного
здівання, отримаємо
D[X ±Y] = М[Х
2
]
± 2 М[Х]
•
M[Y] + M[Y
2
]
- М
2
[X] + 2 M[X]M[Y] - М
2
[Y ] =
= (М[Х
2
]-М
2
[Z]) + (М[У
2
]-M
2
[Y}) = D[X] + D[Y].
Такий самий вираз можна отримати для дисперсії суми декількох взаємно
залежних доданків.
Теорема 4. Дисперсія суми сталої величини і випадкової дорівнює дисперсії
падковоївеличини.
D[C + Х] = D[X].
Дана теорема є наслідком 1-ої та 3-ої теорем.
(2.96)

Елементи теорії ймовірностей 99
Теорема 5. Дисперсія добутку двох незалежних випадкових величин X і
У
визначається за формулою
D[XY] = D[X]D[Y] + m
2
x
D[Y] + m
2
y
D[X]. (2.97)
Для взаємно незалежних величин за формулою (2.92) маємо
M[XY] = M[X]M[Y] = т
х
т
у
.
Згідно означення дисперсії запишемо
ДАТ] = M[(XY-т
х
т
у
)
2
] = M[X
2
Y
2
]-2m
x
m
y
M[XY] + тіш] . (2.98)
У випадку незалежних випадкових величин Хта Fбудуть незалежними
і
лкож
і X
2
та Y
2
. Тоді M[X
2
Y
2
] = M[X
2
]-M[Y
2
], a M[XY] = m
x
-m
y
. Із врахуванням цих
виразів та співвідношення (2.98), отримаємо D[XY] = М[Х
2
]
•
M[Y
2
]
-
m
2
x
•
пґ
г
, або,
маючи на увазі що МІХ
2
] - це початковий момент 2-го порядку випадкової
величини X тобто
M[X
2
] = D[X] + ml, або ^^-v,
2
.
Аналогічно
M[Y
2
\ = D[Y] +
m
2
y
і тоді
D[XY] = D[X]D[Y] + ml
•
£)[7] +
m
2
y
•
D[X],
що і треба було довести.
Розглянемо приклади.
Приклад 5. Задано закон розподілу випадкової величини X
Хі
3 5 7 9
Рі
0,4
0,3 0,2
0,1
Потрібно знайти математичне сподівання та дисперсію випадкової величини X,
Розв'язання. Скористаємося виразами (2.61) і (2.71)
™
х
= І
х
іРі =3-0,4 + 5-0,3 + 7-0,2 + 9-0,1 = 5 ,
і=і
D
x
= І(х, - т
х
)
2
р, = (3 - 5)
2
•
0,4 + (5 - 5)
2
•
0,3 + (7 - 5)
2
•
0,2 + (9 - 5)
2
• 0,1
= 4.
і=І

Розділ II
Триклад
6.
Зі іайти математичне сподівання кількості попадань м'ячем у корзину
двох киданнях, якщо ймовірність одного попадання дорівнює 0,4.
Розв'язаний. Складемо ряд розподілу, для чого обчислимо q = 1 - 0,4 = 0,6
звірність не попасти у корзину при одному киданні), та, використавши
мулу Бернуллі (2.40), обчислимо ймовірності
р
0
=Clp°q
2
=q
2
= 0,6
2
=0,36 (ймовірність не попасти у корзину при двох
іннях),
р
х
= C\p
]
q
]
=2-0,4-0,6 = 0,48 (ймовірність раз попасти у корзину при двох
іннях),
р
2
-C
2
p
2
q° = р
2
=0,4 = 0,16 (ймовірність два рази попасти у корзину при
с киданнях),
Хі
0 1
2
Рі
0,36
0,48 0,16
\ тепер за формулою (2.61) знайдемо математичне сподівання кількості
адань м'ячем у корзину т
х
= 0
•
0,36 +1
•
0,48 + 2
•
0,16 = 0,8.
Приклад 7. Задано випадкову величину Хз математичним сподіванням т
х
= 2
сперсією D = 10. Потрібно знайти математичне сподівання і дисперсію
адкової величини Y = 2х + 5.
Розв
'язання.
Скористаємося властивостями математичного сподівання та дисперсіі
M[Y] = М[2х +
5]
= 2 М[Х] + М[5] = 2 М[Х] +
5
= 2- 2 +
5
= 9,
D[Y] = D[2X +
5]
=
4D[X]
+ Д[5] =
4D[X]
= 4
•
10 = 40 .
§ 2.4. Деякі закони розподілу випадкових величин
2.4.1. Біноміальний розподіл
Розглядаючи в § 2.2 теорему про повторення випробовувань, ми отримали
(2.37), який назвали біноміальним розподілом ймовірностей. Кожний член
у означає ймовірність події В
т
(т = ..., п)
Р(В
т
) = р
я
(т) = с; PV~
и
(/>
+ * = !),
полягає в тому, що деяка подія А з'явиться рівно т разів в п випробовуваннях. При
му в кожному окремому випробовуванні подія А з'являється з ймовірністю р.
