Захаров Н.М., Кулик Н. А Сборник задач по теоретической механике для контрольных и расчетно-графических работ
Подождите немного. Документ загружается.

41
(в неподвижной шарнирной опоре D – две составляющие одной неизвест-
ной по величине и направлению силы реакции
D
R
). Следовательно, для их
определения необходимо иметь 5 независимых уравнений. Но, оставаясь в
рамках теоретической механики и исходя только из уравнений равновесия
твердого тела, получить такое количество независимых уравнений невоз-
можно. Дело в том, что количество таких (независимых между собой)
уравнений равновесия определяется не особенностями рассматриваемой
системы (конструкции, механизма и т. п.),
а исключительно видом систе-
мы сил, приложенной к ней (сходящаяся, произвольная плоская, произ-
вольная пространственная или какая-то иная). Например, в случае произ-
вольной плоской системы сил таких уравнений можно составить только 3.
Тем не менее, задача является статически определимой, т. е. все 5 неиз-
вестных внешних реакций могут быть найдены. Но для
этого придется до-
полнительно рассматривать равновесие отдельно взятых частей конструк-
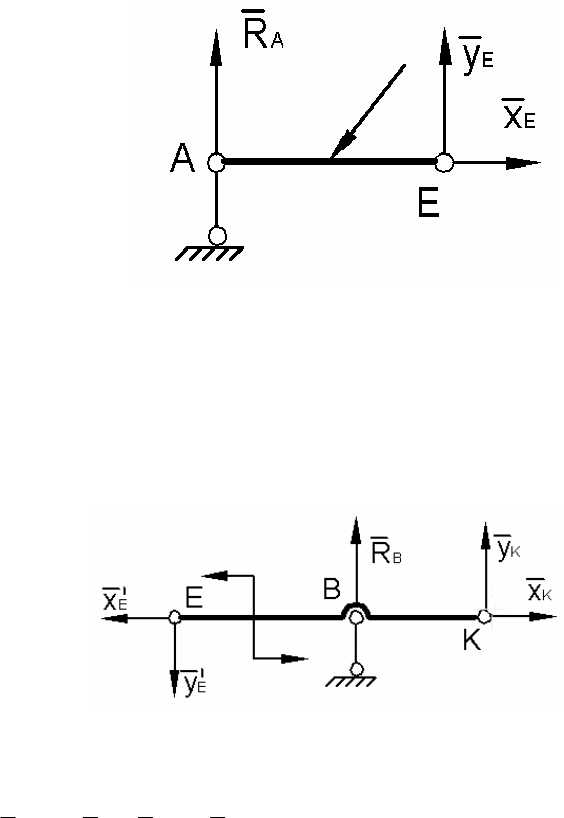
ции. Например, рассматривая только её часть
АЕ (рис. П.12).
Из уравнений равновесия (для
этой части конструкции можно со-
ставить именно 3 не-зависимых
уравнения равновесия, поскольку
действующая на
АЕ система сил
также произвольная плоская) не-
трудно определить и силу
A
R
(кото-
рая является внешней силой и для
АЕ
и для всей конструкции АЕКD в це-
лом) и силу реакции в шарнире
Е
(с составляющими). Они – внешние
Рис. П.12
для АЕ, но внутренние для всей конструкции в целом. После того, как силы
Х
Е
и Y
Е
найдены, можно рассмотреть равновесие следующей части конст-
рукции –
ЕК (рис. П.13).
При построении расчетной
схемы необходимо учесть, что си-
лы, действующие на эту часть
конструкции со стороны
АЕ, т. е.
давления в точке Е, численно рав-
ны найденным выше реакциям:
EE
XX
′
= ;
EE
YY
′
= ,
Рис. П.13
но их направления противоположны этим реакциям:
EE
XX
=
− ;
EE
YY
=
− ,

42
Именно с учетом этого обстоятельства и показаны силы
E
X
′
,
E
Y
′
на рис. П.13.
Снова замечаем, что в рассматриваемых фрагментах задачи и конст-
рукции 3 неизвестных
B
R
,
K
X
,
K
Y
. Но так как на балку ЕК действует про-
извольная плоская система сил, то можно составить именно 3 независимых
уравнения ее равновесия. Следовательно, задача решается и все 3 неиз-
вестные
B
R
,
K
X ,
K
Y будут найдены.
Далее можно рассмотреть либо часть
КD конструкции, либо всю
конструкцию целиком. В последнем случае неизвестными будут
C
R
,
D
X ,
D
Y , т. к.
A
R
и
B
R
уже найдены. Снова можно составить 3 независимых
уравнения равновесия и из них найти эти оставшиеся 3 неизвестные силы.
Подведем итоги. Внутренние силы существуют во всех телах, систе-
мах, конструкциях. В целом они уравновешиваются, но для каждой отдель-
но взятой части системы (конструкции) некоторые из них становятся внеш-
ними. При рассмотрении равновесия какой-
либо части конструкции (систе-
мы) с такими «новыми» внешними силами обращаются как и со «старыми»,
в частности, эти силы входят в уравнения равновесия и при определенных
условиях могут быть найдены методами теоретической механики. Это – так
называемые «статически определимые задачи», в которых количество неиз-
вестных сил и число независимых уравнений равновесия, которые
можно
составить для данной системы сил, равны между собой.
После определения всех внешних (для конструкции в целом) неиз-
вестных сил можно выполнить проверку решения задачи обычным прие-
мом – составить одно (или несколько) уравнений равновесия, неиспользо-
ванных при определении неизвестных. Например, это могут быть уравне-
ния равновесия конструкции (системы) в целом.
Так, «расчленением» составной конструкции на отдельные части и
рассмотрением их равновесия решаются задачи С-4, С-5, С-6, С-7. Они от-
личаются друг от друга только количеством тел, из которых состоит слож-
ная конструкция, находящаяся под действием произвольной плоской сис-
темы сил и закрепленная неподвижно при помощи тех или иных опорных
устройств. Ниже
рассмотрены примеры решения подобных задач.
Пример 6
Определение реакций внешних опор и давления
во внутреннем шарнире составной конструкции
Составная конструкция состоит из двух балок BA и AE, соединенных
шарниром
А. Определить реакции внешних опорных стержней в точках В, Е
и неподвижной шарнирной опоры
D, удерживающих конструкцию в равно-
весии при действии на нее произвольной плоской системы сил (рис. П.14).
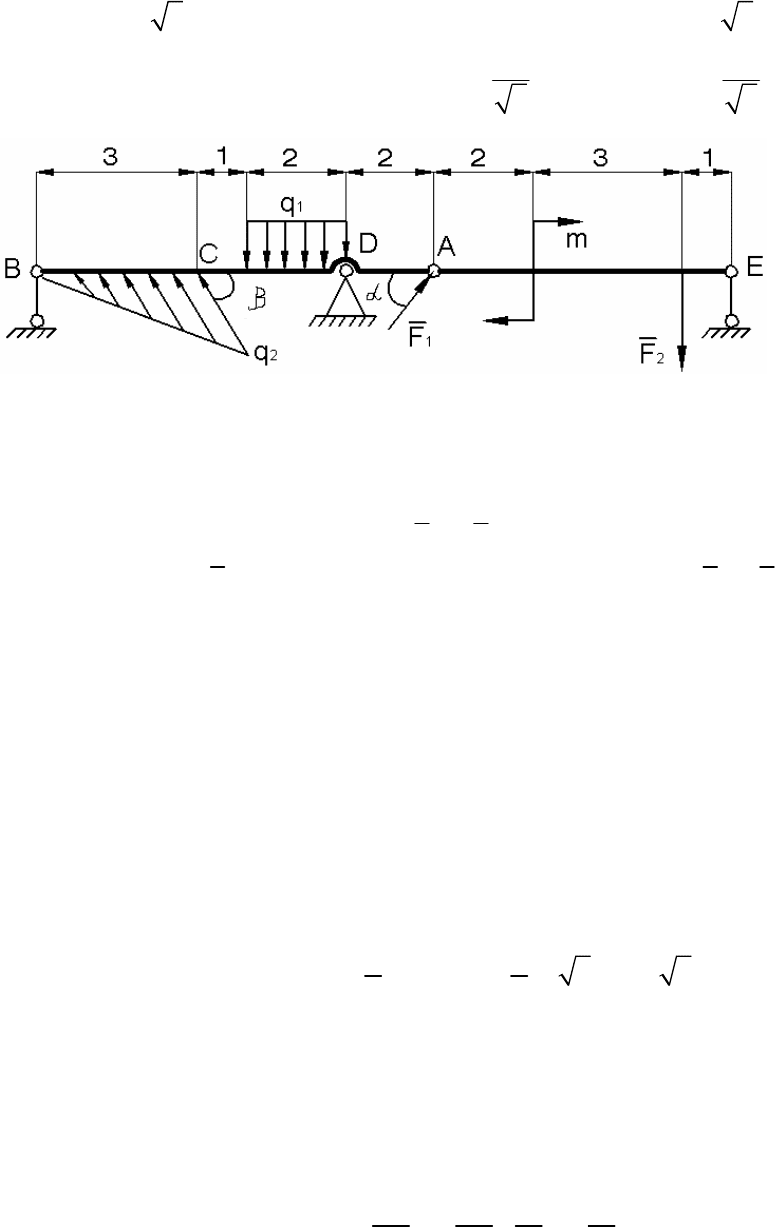
43
Определить также давление в соединенном (внутреннем) шарнире А.
Дано:
1
65 кНF = ; F
2
= 9 кН; q
1
= 3 кН/м; q
2
= q
max
= 25 кН/м;
m = 3 кН⋅м; tgα = 2; tgβ = 0,5; (sin α = cosβ =
2
5
; cosα = sin β =
1
5
).
Рис. П.14
Решение
Для составной конструкции в целом имеем 4 неизвестных внешних
реакции (реакции опорных стержней
B
R
,
E
R
и две составляющие неиз-
вестной силы реакции
D
R
неподвижной шарнирной опоры D –
D
X ,
D
Y ).
Независимых уравнений равновесия всей конструкции в целом (если
воспользоваться аксиомой отвердевания) – только 3, т. к. действующая на
конструкцию система сил является произвольной плоской. Этого не доста-
точно для определения четырех неизвестных. Поэтому воспользуемся ме-
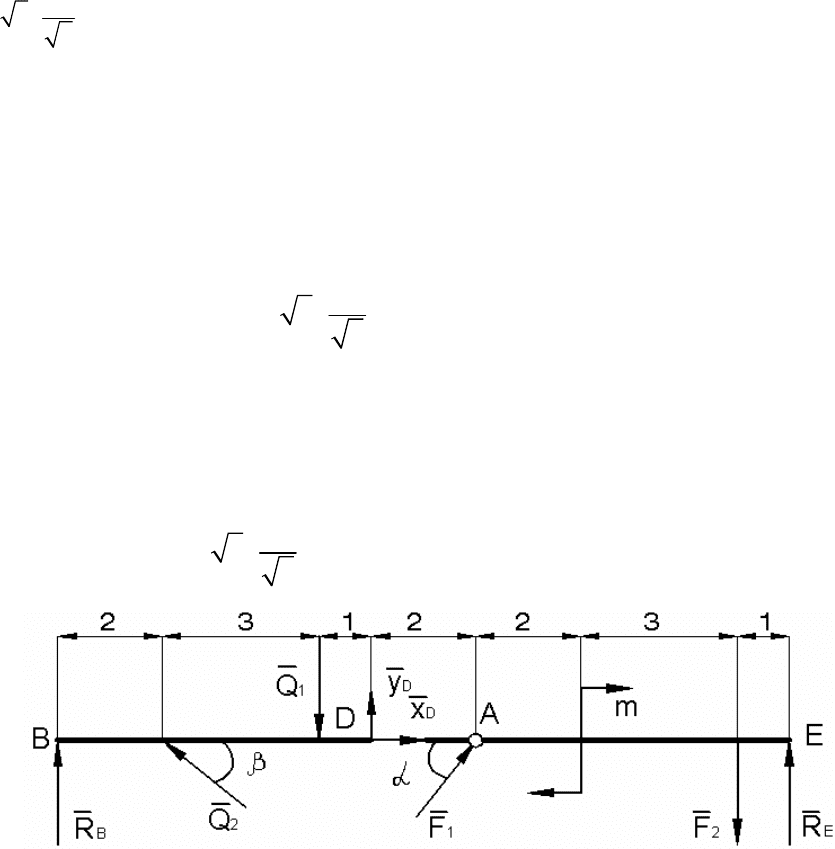
тодом расчленения составной конструкции и будем рассматривать равно-
весие её отдельных частей
ВА и АЕ, полученных расчленением конструк-
ции по внутреннему шарниру
А. Освободим каждое из них от внешних
связей и заменим их действие искомыми силами реакций (рис. П.15, а).
Распределенные нагрузки заменим их равнодействующими:
111
32 6 кНQql=⋅=⋅= ;
2max2
11
253 35 кН.
22
Qql=⋅ ⋅=⋅ ⋅=
Линия действия силы Q
1
проходит через середину участка, где дей-
ствует нагрузка q
1
, а линия действия силы Q
2
проходит через точку L, де-
лящую участок ВС на части 2 : 1, т. е. BL = 2 м; LC = 1 м.
Силы, действующие на каждую часть конструкции в точке А, между
собой равны, но направлены в противоположные стороны:
A
A
XX
′
= ;
A
A
YY
′
=
;
A
A
XX
′
↑↓ ; .
A
A
YY
′
↑↓

44
Рис. П.15.
а) левая часть конструкции; б) правая часть конструкции
В первую очередь рассматриваем равновесие тела АЕ, т. к. среди
внешних сил, действующих на него, только 3 неизвестных, тогда как по-
добных сил, приложенных к телу АВ – 5. При этом на каждое из тел дейст-
вует произвольная плоская система сил, для которых можно составить
только по 3 независимых уравнения равновесия. Выбираем оси Х и
У и со-
ставляем уравнения равновесия тела АЕ.
1) 0
KX
F =
∑
:
1
cos 0
A
XF
′
−+ α=;
A
X
′
−
+
65
⋅
1
5
= 0;
A
X
′
= 6 кН.
2)
()
0
Ek
mF=
∑
:
12
sin 0
A
FAEYAEmFNE
′
−⋅ α⋅ + ⋅ −+ ⋅ =;
2
65 6 6 3 91 0
5
A
Y
′
− ⋅ ⋅+ ⋅−+⋅=
;
72 6 3 9 0
A
Y
′
−
+ ⋅−+=
;
11 кН
A
Y
′
=
.
3)
()
0
Ak
mF=
∑
:
2
0
E
RAEFANm⋅−⋅−=; 6 9 5 3 0
E
R
⋅
−⋅−=;
6480
E
R ⋅− =; 8 кН
E
R
=
.
Проводим проверку правильности решения этой части задачи:
0
KY
F =
∑
:
12
sin 0
AE
YF FR
′
−+⋅ α− + =
;
2
11 6 5 9 8 0
5
−
+⋅−+=
;
20 20 0−+ =; 0 0
=
.
Рассматриваем равновесие тела АВ. Имеем:
6 кН
AA
XX
′
== ; 11 кН.
AA
YY
′
=
=
Остальные неизвестные находим из уравнений равновесия тела АВ.
4) 0
KX
F =
∑
: X
D
+ X
A
– Q
2
⋅cosβ = 0;
2
635 0
5
D
X
+
−⋅=
; 0
D
X = .
45
5)
()
0
Bk
mF=
∑
:
21
sin 0
DA
Q BL Q BP Y BD Y BA⋅β⋅ +⋅ +⋅ +⋅ =;
1
35 2 65 6 118 0
5
D
Y⋅⋅−⋅+⋅+⋅=
;
630 6880
D
Y
−
+⋅+=
;
64/ 6 10,67 кН
D
Y
=
−≈−
.
6)
()
0
Dk
mF=
∑
:
21
sin 0
BA
R DB Q DL Q DP Y DA−⋅ −⋅β⋅ +⋅ +⋅ =;
6126 22 0
B
R−⋅−++=
;
16/ 6 2,67 кН
B
R
=
≈
.
Проводим проверку правильности решения этой части задачи:
0
KY
F =
∑
:
21
sin 0
BDA
RQ QYY
+
⋅β−++=;
1
2,67 3 5 6 10,67 11 0
5
+⋅−− +=
; 00
=
.
Выполним проверку правильности решения всей задачи, для чего со-
ставим уравнение равновесия всей конструкции в целом (рис. П.16).
()
0
Ak
mF=
∑
:
21 2
8sin632 5 60
BDE
RQ QY mFR
−
⋅− ⋅ β⋅+ ⋅− ⋅− − ⋅+ ⋅=;
1
2,67 8 3 5 6 6 3 10,67 2 3 45 48 0
5
−⋅−⋅⋅+⋅+ ⋅−−+=
; 0 0.=
Рис. П.16
Выполненная проверка подтверждает правильность решения всей
задачи.
Примечание. Силы давления в шарнире А будут иными, если силу F отнести к
другому телу, но при этом реакции опор В, Е и D останутся без изменения.
Пример 7
Определение опорных реакций составной рамы
и давления во внутреннем шарнире С
Составная конструкция ACD имеет соединительный шарнир в точке
С и опоры в точках А и D. Определить реакции внешних опор и давления в
шарнире С.
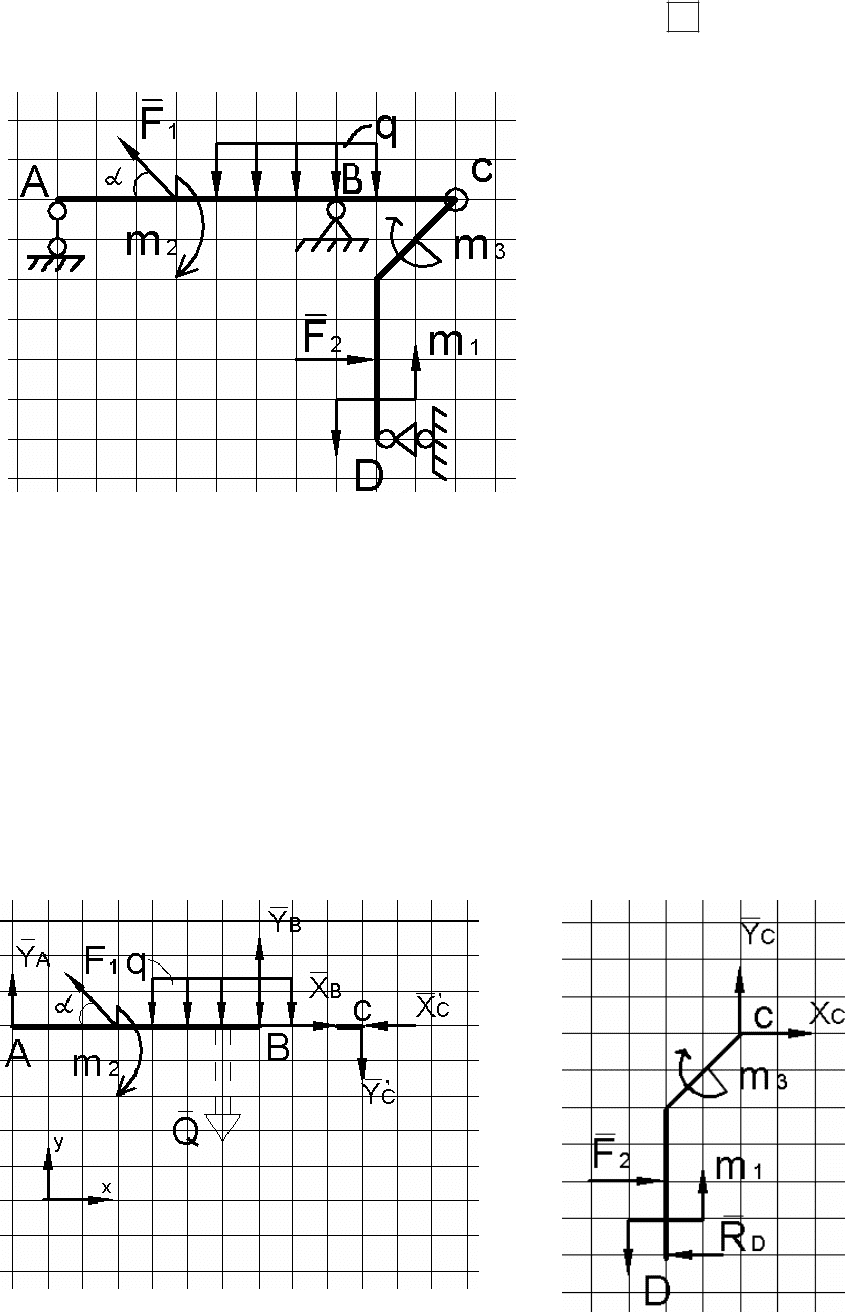
46
Для примеров 7 –9 принять масштаб построений: 1 м
1 м
Рис. П.17
Дано:
sinα = 0,8; cosα = 0,6;
F
1
= 50 кН; F
2
= 30 кН;
q = 10 кН/м; m
1
= 100 кН⋅м;
m
2
= 60 кН⋅м; m
3
= 40 кН⋅м.
Решение
В равновесии под действием произвольной плоской системы сил на-
ходится составная рама, состоящая из 2-х частей (АС и DC), соединенных в
точке С внутренним шарниром. Для нахождения опорных реакций и дав-
ления во внутреннем шарнире расчленим систему на отдельные части, заме-
няя действие отброшенной части реакциями шарнира С, а внешние опоры
–
их реакциями (рис. П.18).
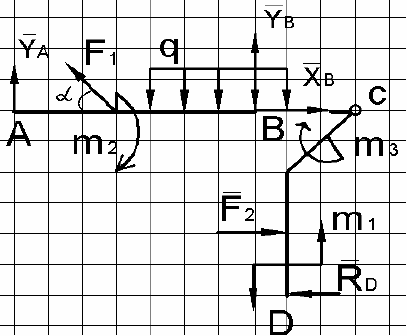
Начнем рассматривать равновесие части конструкции DC (рис. П.19),
т. к. число неизвестных сил, действующих на нее меньше (равно трем).
Рис. П.18 Рис. П.19
47
Тело DC
Составляем уравнения равновесия и решаем их:
0
KY
F =
∑
:
0
c
Y =
.
(
)
0
Ck
mF
=
∑
:
12 3
640
D
RmFm
−
⋅+ + ⋅− =
;
6 100 30 4 40 0
D
R
−
⋅+ + ⋅− =; 30 кН
D
R
=
.
0
KX
F
=
∑
:
2
0
CD
XFR+− =; 30 30 0
C
X
+
−=; 0
c
X = .
Тело AC
Учитывая, что 0 кН;
сс
XX
′
== 0
CC
YY
′
=
= составляем уравнения
равновесия тела АС, предварительно заменив распределенную нагрузку ее
равнодействующей Q, равной 10 4 40 кНQql
=
⋅= ⋅ = .
Линия действия этой силы проходит через середину участка с рас-
пределенной нагрузкой q (см. рис. П.18).
(
)
0
AK
mF =
∑
:
12
sin 3 6 7 10 0
Bc
FmQYY
′
⋅α⋅−−⋅+⋅−⋅=;
50 0,8 3 60 40 6 7 0
B
Y
⋅
⋅− − ⋅− ⋅=
;
25,7 кН
B
Y
=
.
(
)
0
BK
mF =
∑
:
12
7sin4 130
A с
YF mQY
′
−⋅−⋅ α⋅− +⋅−⋅=;
7500,8460400
A
Y−⋅−⋅ ⋅− + =; 25,7 кН
A
Y
=
− .
0
KX
F =
∑
:
1
cos 0
CB
XXF
′
+
−⋅ α=; 0500,60
B
X
−
+−⋅=; 30 кН
B
X = .
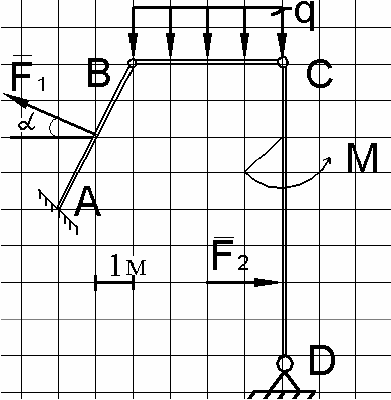
Выполним проверку правильности решения, для чего рассмотрим
равновесие всей конструкции в целом (рис. П.20).
Рис. П.20
Составим уравнение ее равновесия в виде:
(
)
0
CK
mF
=
∑
:
12 321
10 sin 7 4 4 3 4 6 0
ABD
YF mqYmFmR− ⋅ − α⋅− +⋅⋅− ⋅− + ⋅+ − ⋅=.
48
После подстановки в уравнение заданных величин (сил, моментов и т. п.),
а также найденных при решении задачи сил реакций опор получаем:
25,7 10 50 0,8 7 60 10 4 4 25,7 3 40 30 4 100 30 6 0⋅−⋅ ⋅−+⋅⋅− ⋅− +⋅+ −⋅=;
637,1 637,1 0
−
= .
Следовательно, внешние опорные реакции определены верно.
Пример 8
Определение реакций внешних опор составной конструкции
(система трех тел)
Плоская рама, состоящая из 3-х тел, соединенных шарнирами В и С,
находится в равновесии под действием произвольной плоской системы сил
(рис. П.21). Определить реакции внешних опорных устройств, а также дав-
ления в шарнирах В и С и выполнить проверку правильности решения.
Рис. П.21
Дано:
F
1
= 25 кН; F
2
= 20 кН;
q = 10 кН/м; М= 40 кН⋅м;
sinα = 0,6; cosα = 0,8.
Линейные размеры принять непо-
средственно из рис. П.21, выполненного
в указанном масштабе.
Решение
Данная конструкция представляет собой систему 3-х тел, соединен-
ных шарнирами В и С. Для определения реакций опор и давлений в шар-
нирах расчленим систему на отдельные части, заменив действие всех свя-
зей их реакциями.
В точке А тело АВ закреплено жестко. Заменим жесткую заделку А систе-
мой сил реакций X
А
, Y
А
, m
А
, выбрав их направления произвольно (см. рис. П.21).
В точке D тело закреплено при помощи неподвижной шарнирной опоры,
реакцию которой представим в виде системы сил (X
D
, Y
D
). Реакции шарни-
ров В и С также представим в виде систем попарно равных сил (X
B
= X′
B
, Y
B
= Y′
B
,
X
C
= X′
C
, Y
C
= Y′
C
) и будем считать, что силы, помеченные штрихами, дей-
ствуют на среднюю часть конструкции – ВС (рис. П.22, б).
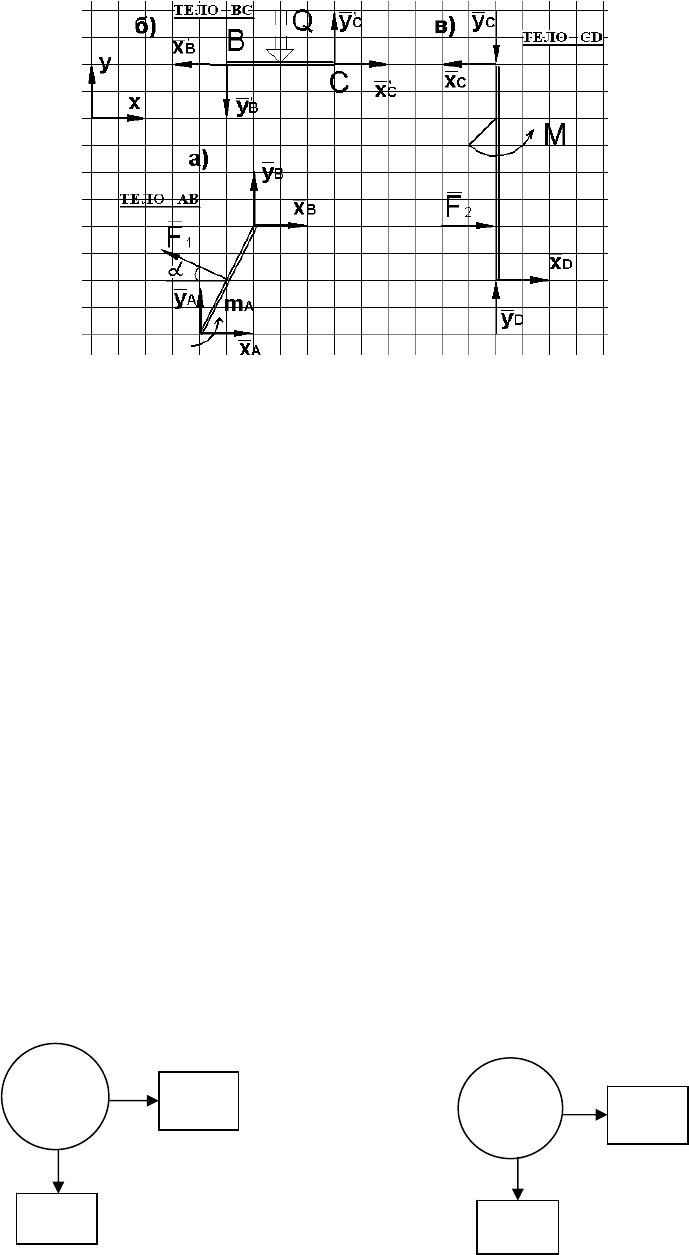
49
Рис. П.22
Вычислим равнодействующую распределенной нагрузки и прило-
жим ее в середине участка распределения 441040 кН.QqBCq
=
⋅=⋅=⋅=
При рассмотрении равновесия каждого тела можем составить только
3 независимых уравнения равновесия, т. к. на любое из них (АВ, ВС и CD)
действует произвольная плоская система сил, состоящая частично из за-
данных сил и частично из сил, которые необходимо определить.
Таким образом, суммарное число независимых уравнений равнове-
сия равно 9. Столько
же и неизвестных сил (в точке А – 3, в точках В, С и D –
по 2 в каждой). Следовательно, задача статически определимая. Трудность ее
решения состоит в том, что на каждое отдельно взятое тело из этой системы тел
действует больше 3-х неизвестных сил: на тело АВ – 5, на тела ВС и CD – по 4).
Рассматривая
равновесие каждого отдельно взятого тела можно сна-
чала определить лишь некоторые из неизвестных сил, действующих на не-
го. Например, из уравнений равновесия тела ВС можно сразу найти силы
Y′
B
и Y′
C
, а из уравнений равновесия тела CD – силы X
D
и X
C
.
Схематически этот процесс можно представить в виде следующего
алгоритма (рис. П.23):
Рис. П.23. Возможные варианты первоочередного определения
некоторых неизвестных сил реакций
ВС
Y′
C
Y′
В
CD
X
C
X
D
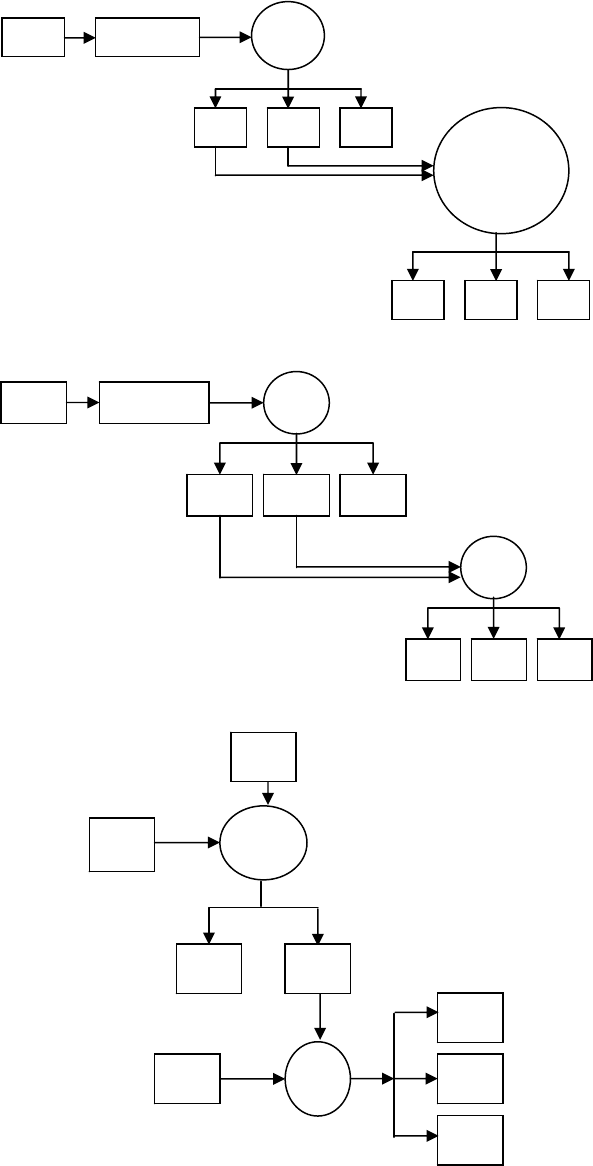
50
Дальнейшее решение задачи можно провести различными путями:
(рис. П.24, П.25, П.26).
Рис. П.24
Рис. П.25
Рис. П.26
Общее число уравнений равновесия – 9, что соответствует числу не-
известных величин. Расчет можно начать или с тела ВС или с тела DC.
Y
B
X
D
BC
D
X
B
Y
D
A
B
Y
B
Y
A
X
A
m
A
X
C
X′
C
= X
C
B
Y′
B
Y′
C
X′
B
A
X
A
m
A
Y
A
C
Y′
C
Y
C
= Y′
C
Y
D
X
D
X
C
Вся кон-
струкция
в целом
Y
A
X
A
m
A
