Захаров Н.М., Кулик Н. А Сборник задач по теоретической механике для контрольных и расчетно-графических работ
Подождите немного. Документ загружается.

141
Здесь векторная формула дополнена таблицей анализа величины и
направления каждого из векторов, входящих в формулу.
Направление вектора
BA
a
τ
показываем по перпендикуляру к АВ предпо-
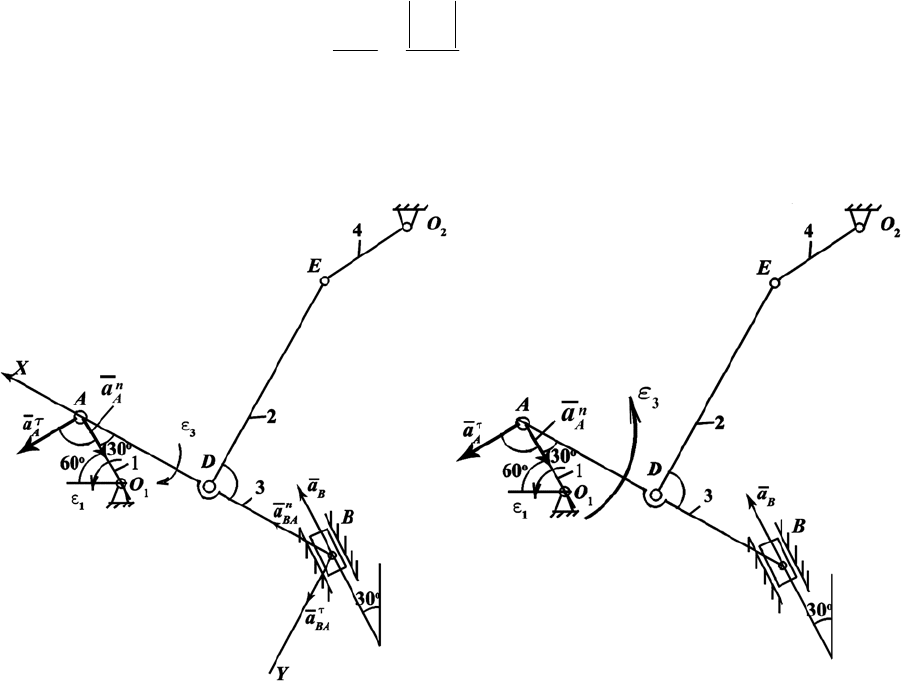
ложительно (рис. П.19), после решения уравнения уточним это направление.
Проводим оси координат и проецируем векторное уравнение на оси X и Y.
Проецируя уравнение на ось X, получаем
cos30 cos60 cos30
nn
BAABA
aaaa
τ
°= °− °+
откуда находим:
2
0,72 м/с
B
a =
Так как
0
B
a >
, то вектор
B
a
направлен так, как показано на рисунке.
Проецируя уравнение на ось Y, получаем:
sin 30 sin 60 sin 30
n
BAABA
aaaa
τ
τ
−°= °− °+
.
Подставляя числовые значения, вычисляем
2
3, 58 м/с
BA
a
τ
=− .
Знак (–) показывает, что вектор
ВA
a
τ
имеет направление, противопо-
ложное показанному на рис. П.19.
Находим ε
3
2
3
3
2,56 рад/с .
BA
BA
a
a
AB l
τ
τ
ε= = =
Показываем истинное направление ε
3
на рисунке с учётом получен-
ного знака у вектора
BA
a
τ
(рис. П.20).
Рис. П.19 Рис. П.20
142
Пример 10
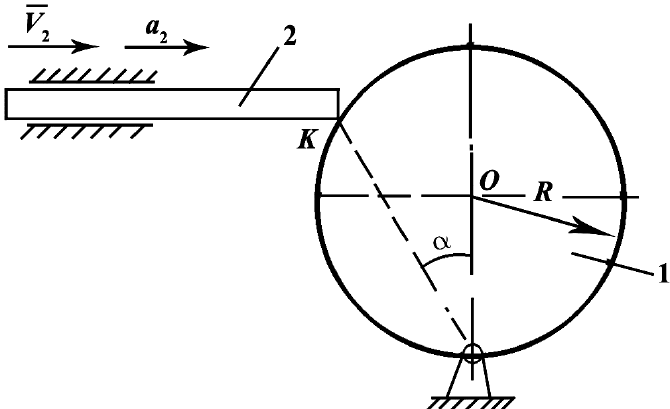
Шток 2, движущийся в прямолинейных направляющих своим кон-
цом К скользит по поверхности круглого эксцентрика (диска) и толкая его
приводит последний во вращательное движение вокруг неподвижной оси.
Шток 2 и эксцентрик 1 расположены и движутся в плоскости рисунка, а
ось вращения эксцентрика перпендикулярна этой плоскости.
Дано:
2
200 см/с;V =
2
2
1000 см/с ;a =
20 см;
R
=
30 .
α
=°
Определить: ω
1
, ε
1
в этот момент времени
Рис. П.21
Решение
По условию задачи задано движение штока 2. С этой скоростью и
ускорением движется и острие К штока относительно неподвижной систе-
мы отсчёта. Но перемещение штока приводит к повороту эксцентрика 1
вокруг оси О
1
. При этом острие К штока скользит по криволинейной по-
верхности эксцентрика, т. е. совершает движение относительно движуще-
гося тела. В соответствии с определениями понятий «сложное, абсолют-
ное, относительное и переносное движение точки» можно говорить о
сложном движении острия К: вращающийся эксцентрик – подвижная сис-
тема отсчёта, а его движение – переносное движение
для острия.
По теореме о сложении скоростей точки, совершающей сложное
движение, можно записать для точки К штока:
абс пер отн
.
К
КК
VVV
=+
143
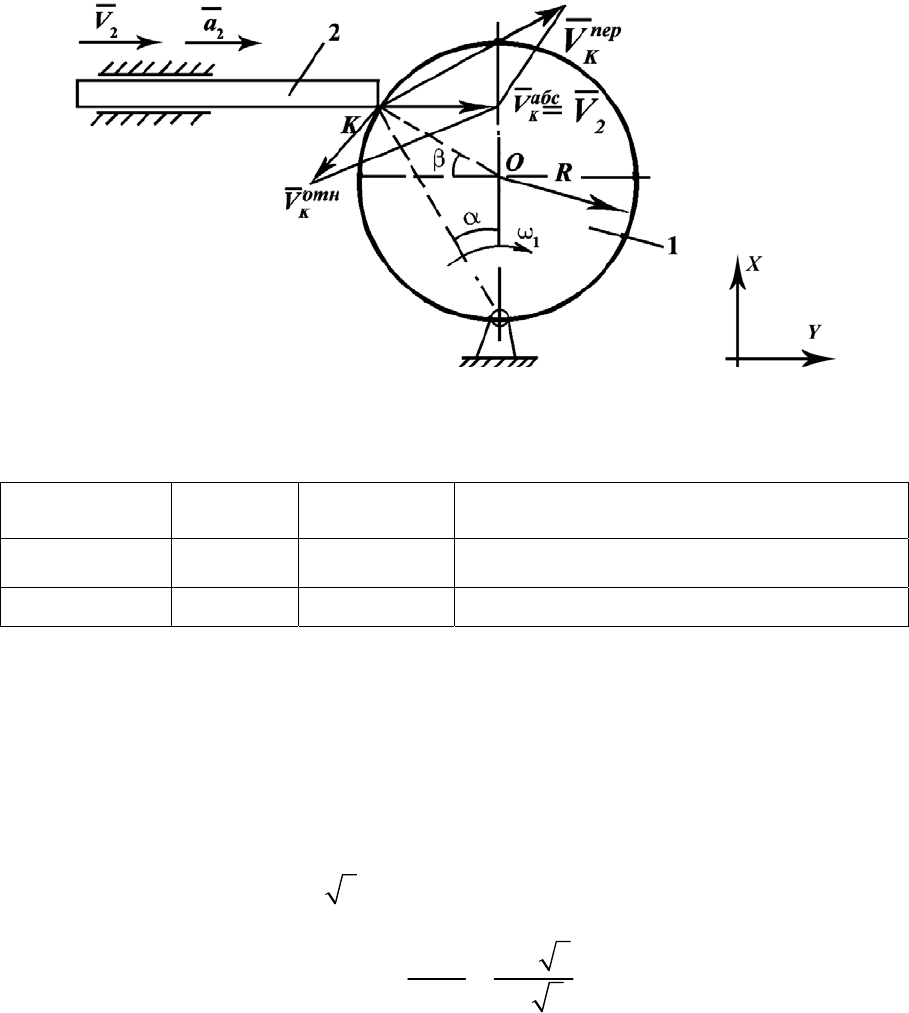
Рис. П.22
Проведём анализ векторного равенства
абс
К
V
=
пер
К
V
+
отн
К
V
величина известна
11
?OKω⋅ =
?
направление известно
1
OK⊥ , изв.
По касательной к поверхности эксцентрика
Выбирая оси X и Y, проектируем на них это векторное уравнение.
−
на ось X:
абс пер отн
cos sin
КК К
VV V
=⋅α−⋅β;
−
на ось Y:
пер отн
0sin cos
КК
VV
=⋅α−⋅β.
Учитывая, что в данном положении системы (при α = 30°) угол β = 30°,
решаем полученную систему уравнений и находим
пер
200 3 346 см/с;
К
V
==
отн
2000 см/с.
К
V
=
Следовательно,
пер
пер
1
1
200 3
10 рад/с.
20 3
К
ОК
V
== = =
ωω
Направление
пер
1
ω=ω показано на рис. П.22. Оно определяется на-
правлением вектора
пер
К
V
, которое получается при разложении вектора
абс
К
V
на составляющие.
Для определения ускорений воспользуемся теоремой Кориолиса,
предварительно определив величину и направление вектора Кориолисова
ускорения острия штока. Поскольку оба составных движения этой точки
происходят в плоскости рисунка, то направление
кор
К
а
находим по правилу
144
Н. Е. Жуковского, повернув вектор
отн
К
V
на 90° в сторону переносного
вращения. Величина ускорения Кориолиса в этом случае находится по
формуле:
кор пер отн 2
2 2 10 200 4000 см/с .
К
К
а V=⋅ω ⋅ =⋅ ⋅ =
По теореме Кориолиса для точки К имеем:
абс пер отн кор
KK
K
K
aaaa=++
.
Но так как переносное движение – вращательное, а относительное
происходит по криволинейной траектории, то ускорение точки К в каждом
из этих движений складывается из касательной и нормальной составляю-
щих:
абс пер. пер. отн. отн. кор
.
nn
KKK
K
KK
aa a a a a
ττ
=++++
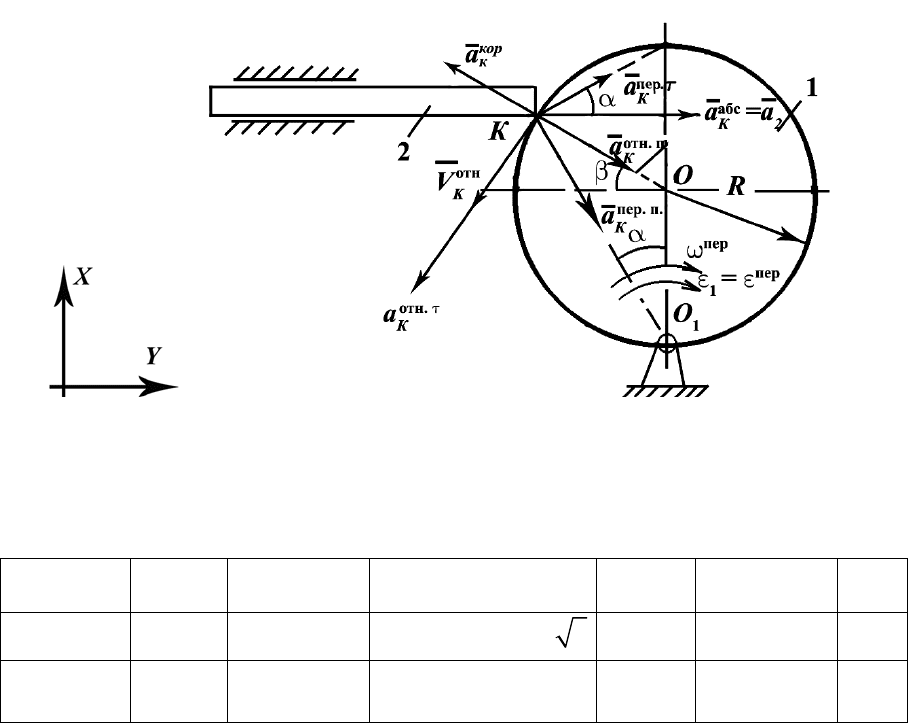
Рис. П.23
Проведём анализ векторного равенства
абс
К
a , и его результат офор-
мим в виде таблицы:
абс
K
a =
пер.
K
a
τ
+
пер.n
K
a
+
отн.τ
K
a
+
отн.n
K
a +
кор
K
a
величина известна
11
?OKε⋅ =
2
11
2000 3OKω⋅ =
?
отн 2
к
()/VR
извес.
направле-
ние
известно
⊥О
1
К
к точке О
1
ОК
⊥
к точке О ивест.
Проекции этого уравнения на оси X и Y приводят к системе:
абс пер. пер.n отн. отн. кор
КК
cos sin sin cos cos ;
аа
n
КК К К
аа а а
ττ
=⋅α+⋅α−⋅β+⋅β−⋅β
пер. пер. отн. отн. кор
К
0 sin cos cos sin sin .
а
nn
КК КК
аа аа
ττ
=⋅α−⋅α−⋅β−⋅β+⋅β
145
Решение её даёт:
отн.
2
2460 см/с
К
а
τ
=− ;
пер.
2
270 см/с .
К
а
τ
=−
Знаки «–» указывают на то, что принятые ранее направления векто-
ров
отн.
K
a
τ
и
пер.
K
a
τ
оказались неверными и в действительности эти векторы
направлены противоположно показанным на рисунке.
Угловое ускорение эксцентрика:
пер.
2
1
1
7,8 рад/с
К
а
ОК
τ
ε= =− , т. е.
2
1
7,8 рад/сε=
и направлено против хода часовой стрелки. Вращение эксцентрика в дан-
ный момент времени происходит замедленно, т. к. направления ε
1
и ω
1
противоположны.
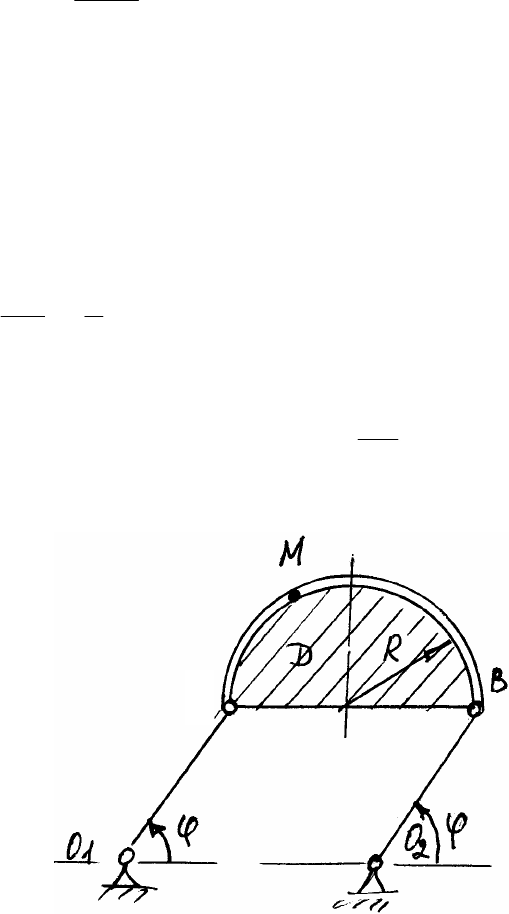
Пример 11
Точка М движется по поверхности тела D по закону
отн
16
Ssin см.
36
АМ t
ππ
∪= = Определить абсолютную скорость и абсолют-
ное ускорение точки М при
1
1 сt
=
, если тело D приводится в движение
вращением кривошипа О
1
А по закону
2
2
t
π
ϕ= рад. На рисунке показано
положение точки М, соответствующее
0
M
S > .
Рис. П.24
Дано:
12
20OA OB==
см, 16
R
=
см.
А

146
Решение
Точка М совершает сложное движение, т. к. она перемещается по по-
верхности движущегося тела D. Движение тела D является для точки М
переносным. Особенности механизма и его размеры таковы, что тело D
движется поступательно и каждая его точка описывает окружность одного
и того же радиуса
12
rOAOB==, но центры их для каждой точки тела D-
свои, не совпадающие, ни с точкой O
1
ни с точкой O
2
. Движение точки М
по поверхности тела D – относительное. Оно происходит по заданному за-
кону вдоль криволинейной траектории радиуса R с центром в точке О.
Уточним положения тела D и точки М в заданный момент времени.
Положение тела D относительно неподвижной прямой O
1
O
2
определяется
углом ϕ. При t
1
= 1 c
2
1
1
22
t
π
π
ϕ
==
рад.
Положение точки М на полуокружности ACB определяется дугой.
11
16 16 8
sin sin
363 63
AM t
π
πππ
∪= =π= см.
Это соответствует центральному углу
1
1
8
рад 30 .
316 6
AM
R
∪ππ
α= = = = °
⋅
Выполняем рисунок, соответствующий этим положениям точки М и
тела D (рис. П.25).
Рис. П.25
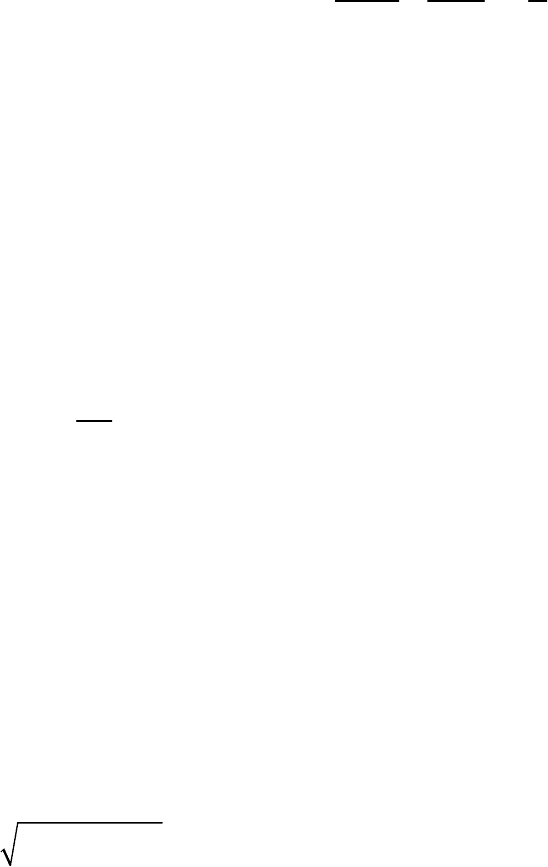
147
Определяем абсолютную скорость точки М по формуле:
абс пер отн
.VVV=+
Относительная скорость точки:
2
отн
отн
16
cos
18 6
dS
Vt
dt
π
π
==
при t
1
= 1 c
V
отн
= 7,58 см/с. Положительный знак V
отн
показывает, что относительное
движение точки происходит в положительном направлении. Вектор
отн
V
направлен по касательной к траектории относительного движения, т. е. по
касательной к дуге окружности радиуса R в положении М
1
.
Переносная скорость той точки тела D, с которой совпадает в момент
времени t
1
c точкой M
1
, но, т. к. тело D движется поступательно, то все его
точки в каждый момент времени имеют одинаковые скорости и ускорения:
они соответственно равны скорости и ускорению точки А.
Итак:
пер А
VV
=
1A
VOA=ω⋅ , где ω – модуль угловой скорости звена О
1
А.
Находим ω:
d
t
dt
ϕ
ω
==π рад/с, при t
1
= 1 c, ω = π рад/c. Показываем
направление ω на рисунке с учётом полученного знака (+), показывающе-
го, что вращение звена О
1
А происходит в направлении возрастания угла ϕ.
Модуль переносной скорости
пер
3,14 20 62,8 см/с
A
VV
=
=⋅= .
Вектор
пер
V
направлен OA
1
⊥
в сторону вращения звена
1
OA.
Модуль абсолютной скорости точки М можно найти аналитически, т. е.
способом проекций. Показываем на рисунке направление осей координат.
отн
абс пер отн
абсY
22
абс абс абс
cos60 62,8 7,58 0,5 59 см/с;
cos30 7,58 0,86 6,56 см/с;
59,4 см/с.
Х
XY
VVV
VV
VVV
=− + °=− + ⋅ =−
=°=⋅=
=+=
Абсолютную скорость точки М можно найти и по теореме косину-
сов, т. е. графоаналитическим.
Определяем ускорение точки М. Так как движение тела Д поступа-
тельное, то абсолютное ускорение точки М находится по формуле:
абс пер отн
.ааа=+
Относительное движение точки – криволинейное, поэтому
отн отн отн
.
n
ааа
τ
=+
148
Переносное ускорение точки М в данный момент времени – ускоре-
ние точки тела D движущегося поступательно. Ускорения всех его точек
одинаковы и равны, например, ускорению точки A.
пер
.
A
aa=
Величина и направление
пер
a
одинаковы с ускорением точки А
пер пер пер
.
n
aaa
τ
=+
Расчетная формула принимает вид:
абс отн отн пер пер
nn
aaaaa
ττ
=+++
.
Вычислим модули всех векторов и покажем их направление на рисунке
3
отн
отн
16
sin
108 6
dV
t
a
dt
τ
π
π
==− ,
при t
1
= 1 c
2
отн
2, 29 см/са
τ
=−
Знаки
отн
V и
отн
a
τ
при t
1
= 1 c разные, т. е. относительное движение за-
медленное (векторы
отн
V
и
отн
a
τ
направлены противоположно друг другу)
22
отн отн
отн
n
VV
a
R
==
ρ
;
при t
1
= 1 c;
2
2
отн
7,58
3,59 см/с .
16
n
a ==
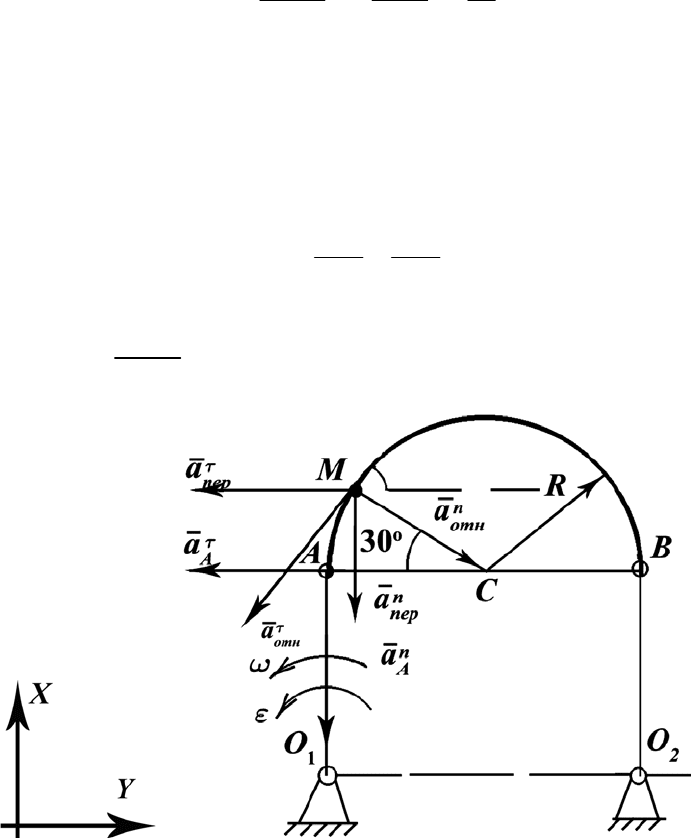
Рис. П.26

149
Вектор
отн
n
a направлен перпендикулярно
τ
отн
a к центру кривизны
траектории относительного движения, т. е. к точке С.
При поступательном переносном движении переносное ускорение
точки М совпадает с ускорением любой точки тела Д, например, точки А.
Поэтому
пер
A
aa=
2
пер 1
nn
A
aa OA==ω ;
при t
1
= 1 c
22
пер
3,14 20 125,6 см/с .
n
a =⋅=
Вектор
пер
n
a
направлен вертикально вниз (
1
OA )
пер 1A
aa OA
ττ
==ε⋅ ;
2
рад/с .
d
dt
ω
ε= =π
Так как знаки ω и ε одинаковы, то вращение звена О
1
А – ускоренное.
пер
3,14a
τ
=⋅20=62,8 см/с
2
.
Вектор
пер
a
τ
направлен перпендикулярно О
1
А, т. е. влево. Показыва-
ем векторы ускорений на рис. П.26.
Модуль абсолютного ускорения находим способом проекций, про-
ецируя выражения
абс
а
на принятые оси координат X и Y:
абс отн отн пер
cos30 cos60
n
X
аа а а
ττ
=°−°−
;
τ
абс отн отн пер
sin 30 sin 60
nn
Y
аа а а=°−°−
при t
1
= 1 c
2
абс
60,8 см/с
X
а =− ;
2
абс
125,8 см/с
Y
а =− ;
22 2
абс абс абсY
139,7 см/с .
X
ааа=+=
Пример 12
Треугольная пластина ADE вращается вокруг оси Z с угловой скоро-
стью
2
0,3 2, 2 рад/сtω= − (положительное направление ω показано на ри-
сунке дуговой стрелкой). По гипотенузе AD движется точка В по закону
2
215 3 смS
А
В tt==+−
(положительное направление отсчёта S от А к D).
Определить абсолютную скорость
абс
V
и абсолютное ускорение
абс
a
точки
B в момент времени t
1
= 2 c.

150
Рис. П.27
Решение
Движение точки В сложное, её
движение по прямой АD является отно-
сительным, а вращение пластины –
переносным. Абсолютную скорость
точки В определим по формуле:
абс пер отн
VVV=+
.
Вычислим скорости, входящие в
это равенство, и уточним их направле-
ния. Относительное движение прямо-
линейное, происходящее по закону
2
215 3 см SAB t t
=
=+ −
, поэтому
отн
15 6VS t
•
=
=−
в момент времени t
1
=
2 c
отн
3 см/сV
=
.
Знак (+) показывает, что вектор
отн
V
направлен в сторону отсчёта по-
ложительных расстояний S, то есть к
точке D (рис. П.28).
Рис. П.28
Переносное движение – это враще-
ние пластины с угловой скоростью ω.
Найдём угловую скорость и угловое
ускорение переносного вращения.
21
0,3 2, 2 сt
−
ω= − ;
2
0,6 ct
•
−
ε=ω= .
При t
1
= 2 c; ω = –1 c
–1
; ε = 1,2с
–2
знаки показывают что в момент време-
ни t
1
= 2 c направление ω противопо-
ложно показанному на рис. П.28 и вра-
щение в этот момент замедленное.
Определим положение точки В в
момент времени t
1
= 2 c:
S
1
= AB
1
= 20 см.
Находим по рис. П.28 расстояние
h
1
точки В
1
от оси вращения:
h
1
= AB
1
sin30° = 10 см.
