Захаров Н.М., Кулик Н. А Сборник задач по теоретической механике для контрольных и расчетно-графических работ
Подождите немного. Документ загружается.


151
Находим V
пер
пер 1
10 см/с.Vh
=
ω⋅ =
Вектор
пер
V
направлен перпендикулярно h
1
в сторону переносного
вращения, т. е. по оси X неподвижных осей координат, проведенных через
точку О. Для определения вектора
абс
V
необходимо сложить векторы
отн
V
и
пер
V
,
которые взаимно перпендикулярны, поэтому
22
абс пер отн
()()VV V=+ в мо-
мент времени t
1
= 2 c V
абс
= 10,4 см/c.
Абсолютное ускорение точки В определим на основании теоремы о
сложении ускорений:
абс пер отн кор
.aaaa=++
Так как переносное движение вращательное, то
пер пер пер
n
aaa
τ
=+
.
Относительное движение прямолинейное, поэтому
отн отн
aa
τ
=
,
отн
0
n
a
=
.
Расчётная формула для определения
абс
а
принимает вид:
абс пер пер отн кор
n
aaaaa
ττ
=+++
.
Вычислим и величины и уточним направление всех векторов , вхо-
дящие в эту формулу.
Находим
отн
а
:
2
отн
отн отн
6 см/с
dV
аа
dt
τ
== =− .
Направление вектора
отн
a
к
точке А.
Находим векторы
пер
n
a
и
пер
a
τ
22
пер 1
10 см/с
n
а h=ω ⋅ = ,
2
пер 1
12 см/с .а h
τ
=ε⋅ =
Вектор
пер
n
a
в плоскости ри-
сунка перпендикулярен оси враще-
ния к точке О
1
.
Рис. П.29

152
Вектор
пер
a
τ
перпендикулярен О
1
В
1
.
Вектор угловой скорости
ω
переносного вращения и вектор
отн
V
образуют угол α = 30°, поэтому модуль Кориолисова ускорения опреде-
лится как
2
кор отн
2 sin 2 3 1 sin 30 3 см/са V=⋅ω⋅ ⋅ α=⋅⋅⋅ °= .
Направление
кор
a
можно найти по правилу векторного произведения:
кор отн
пер
2aV=ϖ × ,
или правилу Н. Е. Жуковского. Для этого вектор
отн
V
спроецируем в плос-
кость, перпендикулярную оси вращения и затем эту проекцию повернём на
90° в сторону ω, т. е. по ходу часовой стрелки. Таким образом, получим
направление
кор
a
. Он направлен перпендикулярно плоскости пластины, т.
е. в направлении оси X.
Для определения
абс
a
воспользуемся осями, проведёнными через
точку О.
Проектируя равенство
абс пер пер отн кор
n
aaaaa
ττ
=+++
на оси X, Y, Z на-
ходим проекции
абс
a
на эти оси:
2
абс пер кор
9 см/с
X
aaa
τ
=−=− ;
2
абс пер отн
sin30 13 см/с
n
Y
ааа=+⋅ °= ;
2
абс отн
cos30 5,2 см/с
Z
аа=⋅ °=
.
Находим значение
абс
а
:
222 2
абс абс абс абс
16,64 см/с .
XYZ
аааа=++=
Пример 13
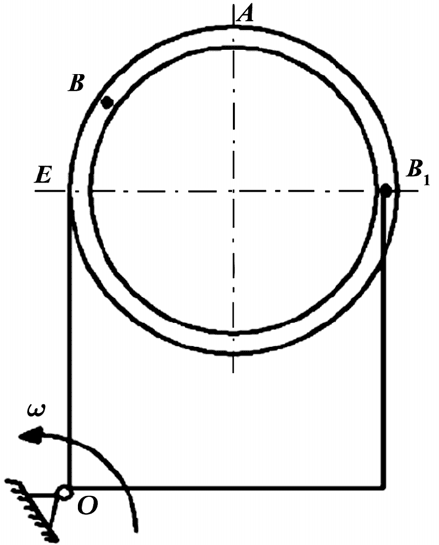
Тело произвольной формы вращается вокруг оси, проходящей через
точку О перпендикулярно плоскости пластины с угловой скоростью
(
)
2
21,5 радttω= − (положительное направление отсчёта ω показано на рис. П.30).
По дуге окружности радиуса R = 0,5 м движется точка В по закону
()
cos м
3
t
S АВ R
∪
π
==π⋅⋅ , t – сек. (положительные отсчёты от А к В).
Определить абсолютную скорость и абсолютное ускорение точки в момент
времени t
1
= 2 c.
153
Решение
Рассмотрим сложное движение точки В. Вращение пластины с угло-
вой скоростью ω = 2t – 1,5t
2
является переносным движением точки. Угло-
вая скорость переносного движения определится при t
1
= 2 c:
ω
1
пер
= 4 – 1,5⋅4 = – 2 с
–2
.
Знак (–) показывает, что направление ω
1
противоположно показан-
ному на рис. П.30
Рис. П.30
Угловое ускорение переносного движения определится
()
пер пер 2
23c ,t
•
−
ε=ω=−
при t
1
= 2 c
пер
2
1
26 4с .
ε
−
=−=−
Показываем направление ω
пер
и ε
пер
на рисунке с учётом полученных
знаков.
Абсолютная скорость точки
абс
V
находится по формуле:
абс пер отн
.VVV=+
Определяем величины, входящие в это равенство.
154
Относительное движение точки происходит по закону
cos .
3
t
S АВ R
∪
π
==π⋅⋅
Устанавливаем, где будет находиться точка В на дуге окружности в
момент времени t
1
:
1
2
cos 0,5
3
SR
π
⎛⎞
=π ⋅ =− π
⎜⎟
⎝⎠
R(м).
Тогда
1
0,5
0,5
SR
АСВ
R
R
π
< = =− =− π (рад).
Знак (–) свидетельствует о том, что точка В в момент времени t
1
= 2 с на-
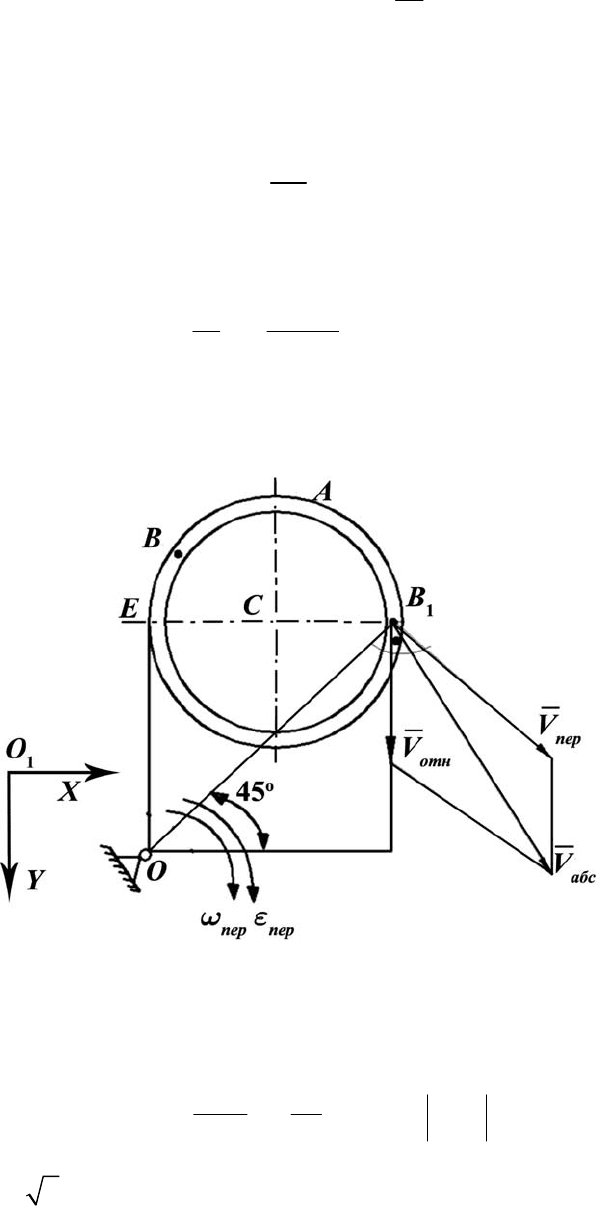
ходится справа от точки А. Показываем её положение на рис. П.31 (точка В
1
).
Рис. П.31
Находим числовые значения
отн
V
и
пер
V
2
отн
sin
33
Rt
VS
•
π
π
==−
;
1
пер пер
OB
V
=⋅
ω
,
где
1
221,41 мOB R== в момент времени t
1
= 2 c.
отн
1,42 м/сV =− ,
пер
21,41 2,82 м/с.V
=
⋅=

155
Показываем направление векторов
отн
V
и
пер
V
с учётом полученных
знаков на рис. П.31. Вектор
пер
V
направлен ⊥ расстоянию ОВ
1
в сторону
переносного вращения, вектор
отн
V
направлен по касательной к траекто-
рии относительного движения в сторону, противоположную положитель-
ному отсчёту дуговой координаты S, т. к. в расчёте получен знак (–).
Проведём координатные оси О
1
XY и спроектируем обе части равен-
ства, определяющего
абс
V
на оси.
На ось Х:
абс отн пер пер
0 cos45 1,99 м/с.
ХХХ
VVV V=+=−⋅°=−
На ось Y:
абс отн пер отн пер
cos 45 3,41 м/с.
YYY
VVV VV=+=+⋅°=
Находим
абс
V
.
22 2 2
абс абс абс
(1,99) (3,41) 3,95 м/с.
Х Y
VVV⇒= + =− + =
Абсолютное ускорение точки В
1
определим по формуле:
абс пер отн кор
.aaaa=++
Переносное движение – это вращение пластины вокруг точки О, поэтому
пер пер пер
.
n
aaa
τ
=+
Относительное движение точки В
1
– криволинейное движение по ок-
ружности радиуса R пластины, поэтому
отн отн отн
.
n
aaa
τ
=+
Расчётная формула для определения
абс
a
принимает вид:
кор
абс пер пер отн отн
.
nn
aaaaaa
ττ
=++++
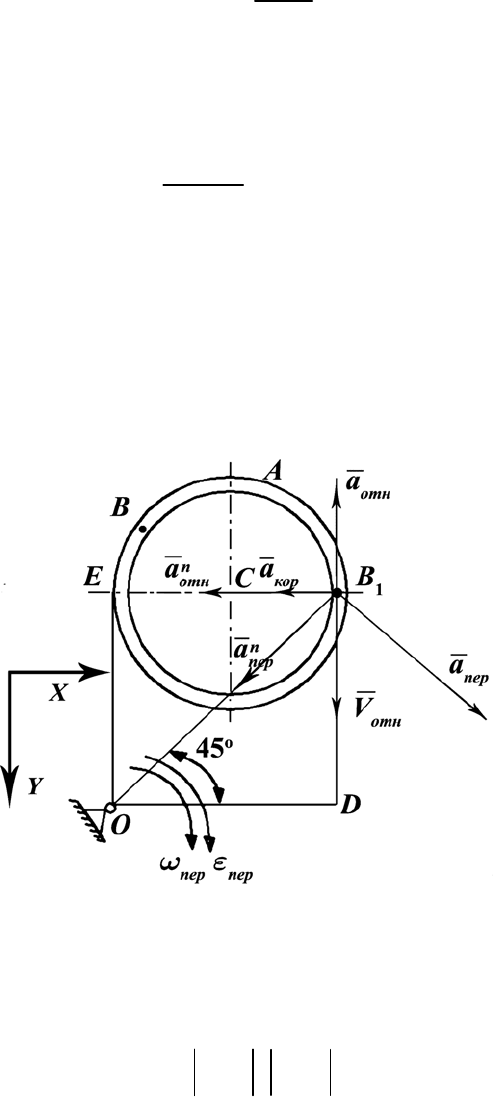
Определим модуль и направление всех векторов, входящих в это ра-
венство (рис. П.32).
22 2
пер пер 1
21,415,64 м/с .
n
аОВ=ω ⋅ = ⋅ =
Вектор
пер
n
а
направлен по прямой В
1
О к центру вращения О.
2
пер пер 1
41,41 5,64 м/саОВ
τ
=ε ⋅ = ⋅ =
.
Вектор
τ
пер
а
направлен перпендикулярно ОВ
1
в сторону
пер
ε .
3
отн
отн
cos
93
dV
R
а t
dt
τ
π
π
⎛⎞
==−
⎜⎟
⎝⎠
156
при t
1
= 2 c,
2
отн
0,86 м/са
τ
=
,
2
отн
отн
отн
n
V
a
=
ρ
,
где ρ
отн
– радиус кривизны траектории точки в относительном движении.
ρ
отн
= R.
2
2
отн
(1, 42)
4,06 м/с .
0,5
n
a
==
Вектор
отн
n
a
направлен перпендикулярно
отн
V
в сторону вогнутости
траектории.
Вектор
отн
a
τ
направлен противоположно вектору
отн
V
, т. к. знаки
отн
V
и
отн
a
τ
противоположны.
Рис. П.32
Находим Кориолисово ускорение
кор
a
.
Модуль Кориолисова ускорения определяем по формуле:
кор
отн пер
2sinαa
V
=⋅
ω
,
где α – угол между векторами
отн
V
и
пер
ω
.
Вектор
пер
ω
направлен вдоль оси вращения пластины перпендику-
лярно к плоскости чертежа, т. е. перпендикулярен вектору
отн
V
, лежащему
в плоскости пластины, значит, α = 90°.
157
Вычисляем
кор
a
при t
1
= 2 c.
2
кор
5, 68 м/с .a =
Направление
кор
a
найдём по правилу Н. Е. Жуковского, поворотом
вектора
отн
V
на 90° в сторону ω
пер
.
Таким образом, значения всех входящих в правые части равенства
В
a
векторов и их направления найдены. Для сложения этих векторов
проводим оси координат и спроектируем обе части равенства, определяю-
щего
В
a
, на эти оси.
На ось Х:
абс отн кор пер пер
cos 45 cos 45
nn
Х
aaа aa
τ
=− − − ⋅ °+ ⋅ °
.
На ось Y:
абс пер пер отн
cos45 cos 45
n
Y
aa a a
τ
τ
=⋅ °+⋅ °−
.
Подставляя числовые значения для момента времени t
1
= 2 c находим:
а
абсX
= – 9,74 м/с
2
;
2
абс
7,15 м/с ;
Y
а =
2222 2
абс абс абс
( ) ( ) 9,74 7,15 12,08 м/с .
Х Y
аа а=+=+=
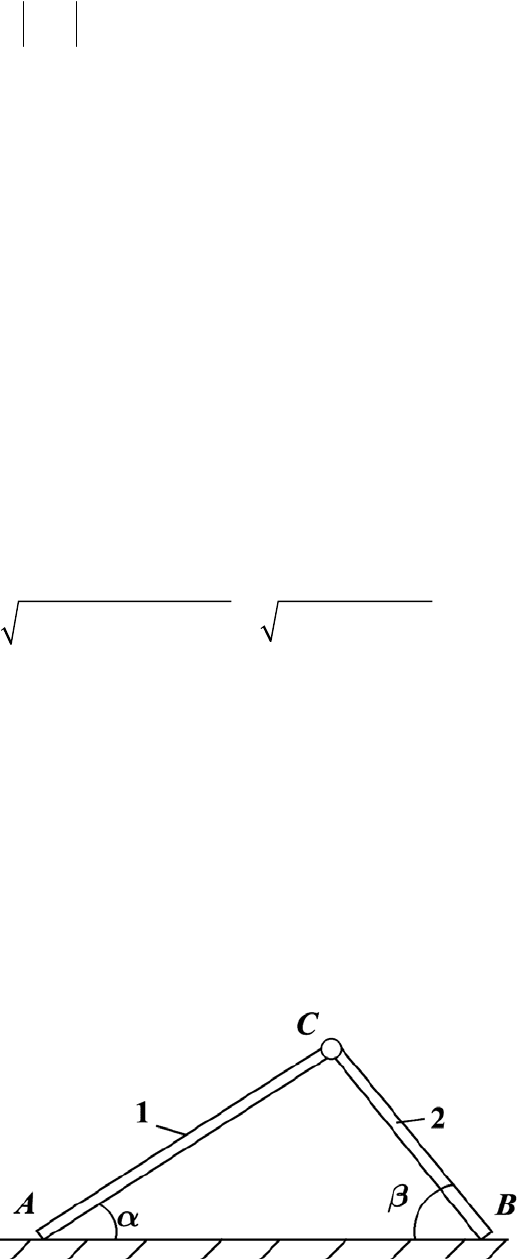
Пример 14
Простейший рычажный механизм с двумя степенями свободы
представляет собой два шарнирно соединённых стержня, свободные концы
которых скользят по общей горизонтальной направляющей. Механизм
расположен в плоскости рисунка (рис. П.33). Определить
с
V
, если
2 м/с
A
V = ; 3 м/с
B
V = , их направления показаны на рисунке. При вычисле-
ниях принять:
АС = 0,8 м, ВС = 0,6 м и в рассматриваемый момент
cosα = 0,8, cosβ = 0,6.
Рис. П.33

158
Решение
Для определения
c
V
воспользуемся теоремой о проекциях скоростей
и применим её отдельно к телу 1 и телу 2.
Рис. П.34
Предположив, что
ССX СY
VV V=+
, можем записать:
1) для тела 1:
A
C
АС АС
Пр V Пр V=
, или
A
CX CY
АС АС АС
Пр V Пр V Пр V=+
(1)
2) для тела 2 аналогично:
BCXCY
BС BС BС
П
р V Пр V Пр V=+
(2)
В заданном конкретном положении механизма выражения (1) и (2)
приобретают вид (рис.П.34):
cos cos sin
,
cos cos sin
ACX CY
BCXCY
VV V
VVV
⋅α= ⋅α+ ⋅α
⎧
⎨
−⋅ β=− ⋅ β+ ⋅ β
⎩
или
2 0,8 0,8 0,6 1,6 0,8 0,6
3 0,6 0,6 0,8 1,8 0,6 0,8
CX CY CX CY
CX CY CX CY
VV VV
VV VV
⋅= ⋅+ ⋅ = +
⎧⎧
⇒
⎨⎨
−⋅ = ⋅ + ⋅ − =− +
⎩⎩
. (3)
Решая полученную систему (3), находим:
0,46 м/с
CX
V = ; 0,48 м/с
CY
V =− ;
22
2,51 м/с
CCXCY
VVV=+= .
Истинную картину движения механизма покажем на рис. П.35.
Рис. П.35

159
ЛИТЕРАТУРА
1. А. А., Яблонский, В. М., Никифорова. Курс теоретической механики. –
Ч. 1. – М.: Высш. шк., 1984 и последующие издания.
2.
М. И., Бать, Г. Ю., Джанелидзе, А. С., Кельзон. Теоретическая
механика в примерах и задачах. – Ч. 1. – М.: Высш. шк., 1984.
3.
Н. Н., Никитин и др. Курс теоретической механики. – М.: Высш. шк.,
1983.
4.
С. М., Тарг. Краткий курс теоретической механики. – М.: Высш. шк.,
1986 г. и последующие издания.
5.
Сборник заданий для курсовых работ по теоретической механике /
Под. общ. ред. А. А. Яблонского. – М.: Высш. шк., 1985.

160
Учебное издание
СБОРНИК ЗАДАЧ
ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
ДЛЯ КОНТРОЛЬНЫХ И РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ
для студентов строительных специальностей
дневной и заочной форм обучения
Редактор Ю. Г. Зеленко
Подписано в печать 8.08.2006. Формат 60х84
1
16
. Гарнитура Таймс. Бумага офсетная.
Печать трафаретная. Усл. печ. л. 9,28. Уч.-изд. л. 9,12.Тираж 195 экз. Заказ 1056.
Издатель и полиграфическое исполнение –
Учреждение образования «Полоцкий государственный университет»
ЛИ № 02330/0133020 от 30.04.04 ЛП № 02330/0133128 от 27.05.04
211440 г. Новополоцк, ул. Блохина, 29
