Захаров Н.М., Кулик Н. А Сборник задач по теоретической механике для контрольных и расчетно-графических работ

Подождите немного. Документ загружается.

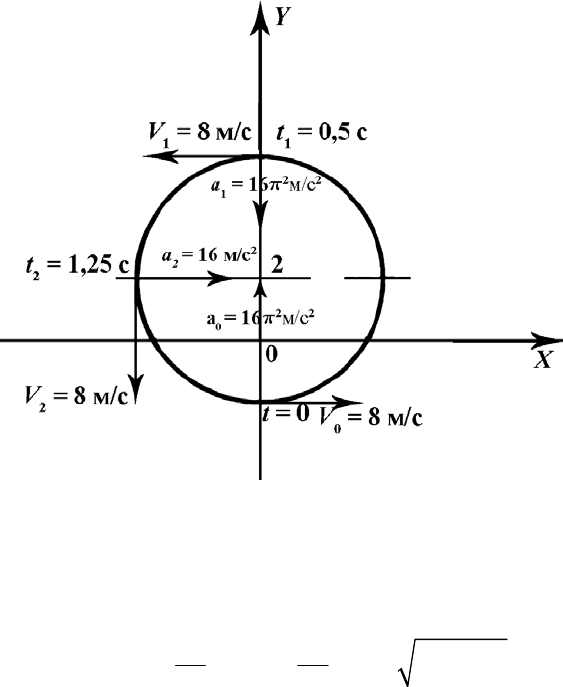
111

периодические функции, изменяющиеся в пределах от –1 до +1, то коор-

дината х движущейся точки плавно изменяется в пределах 4 м 4 м

−≤≤ , а

координата у – в пределах 26 му−≤ ≤ . То есть траекторией точки являет-

ся вся окружность, описываемая уравнением (1). Выполняем рисунок тра-

ектории точки и показываем на нем положения движущейся точки в мо-

менты

0t =

0,5 сt =

1, 25 ct =

. (рис. 1.)

При

0t =

4sin(2 ) 4sin 0 0х t=π==

;

24cos(2 )24cos0 2 м.yt

−π⋅=−=−

При

0,5 сt = :

(

)

4sin2 0,5 4sin 0x =⋅ π⋅ =⋅ π=;

(

)

24cos2 0,5 24cos 6 м.y =−⋅ π⋅ =−⋅ π=

При

1, 25 ct = :

(

)

(

)

4sin2 1,25 4sin2,5 4 мx =⋅ π⋅ =⋅ ⋅π=− ;

(

)

(

)

2 4 cos 2 1,25 2 4 cos 2,5 2 м.y =−⋅ π⋅ =−⋅ ⋅π=

Рис. П.1

Определяем скорость точки. Ее проекции на оси координат и вели-

чина определяются выражением:

= и

= ;

VVV=+

В данном случае:

(

)

8cos2

ππ;

(

)

8sin2

ππ; 8V const

π= ,

т. е. движение точки по траектории – равномерное со скоростью 8 м/сV =π .

112

При

= 0,5 м/с:

(

)

8cos2 8cos 8

Vt=π⋅ π⋅ =π π=−π м/с;

(

)

8sin2 8sin 0

Vt=π⋅ π⋅ =π π=

При t

=1,25 м/с:

(

)

(

)

8cos2 8cos2,5 0

Vt=π⋅ π⋅ =π ⋅π= м/с;

(

)

(

)

8sin2 8sin2,5 8

Vt=π⋅ π⋅ =π ⋅π=−π м/с.

Выбрав масштаб для построения векторов скоростей, показываем на

рисунке траектории скорость точки и ее проекции в моменты времени t

и t

Ускорение точки.

При координатном способе задания движения точки (в системе ко-

ординат ОХY) вычисляются проекции ускорения на координатные оси:

;

aaa

В данном случае:

(

)

16 sin 2

at=− π π

;

(

)

16 cos 2

ππ;

16aconst

π= .

При t

=0,5 м/с:

16 sin 0

a =− π π=

;

16 sin 16

ππ=−π (м/с

При t

= 1,25 м/с:

(

)

16 sin 2,5 16

a =− π ⋅π = π (м/с

);

(

)

16 cos 2,5 0

a =π⋅ ⋅π=.

При криволинейном движении точки ее ускорение раскладывается на ка-

сательную и нормальную составляющие. Их можно вычислить по формулам:

xyy

Va Va

dt V

== ;

a =

(ρ – радиус кривизны траектории).

В данном случае:

= , т. к. 8V const

π= ;

=π м/с

Нормальное ускорение точки направлено к центру кривизны траек-

тории, т. е. к точке

(0, 2) в любом положении точки на этой кривой.

Дуговая координата и пройденный путь.

Если принять:

1. Начало отсчета дуговых координат

S движущейся точки в том поло-

жении, где находилась точка в начальный момент времени

= 0 (т. е. S

= 0).

113

Рис. П.2

2. Направление отсчета положительных значений дуговых коорди-

нат точки – по направлению ее движения.

3. Путь, пройденный точкой к начальному моменту времени

= 0,

равным нулю (

= 0), то дуговая координата S точки в произвольный мо-

мент времени

t и путь, пройденный ею к этому моменту, будут выражаться

одним и тем же уравнением:

8 (м).

SVt t==⋅=π⋅

Невыполнение любого из вышеперечисленных условий приведет к

различным формулам для вычисления дуговой координаты (определяю-

щей положение точки) и пройденного ею пути.

Пример 2

Движение точки М происходит согласно уравнениям (х, у – в м, t – с):

2cos(2 )

t=π;

2sin()yt

−π.

Определить траекторию точки; проанализировать движение точки по

траектории и определить ее скорость и ускорение в моменты времени

= 0 c и

= 1 c.

Решение

1. Чтобы получить уравнения траектории, исключим время t из за-

данных уравнений движения:

cos(2 )

tπ=;

sin ( ) 2ty

=−

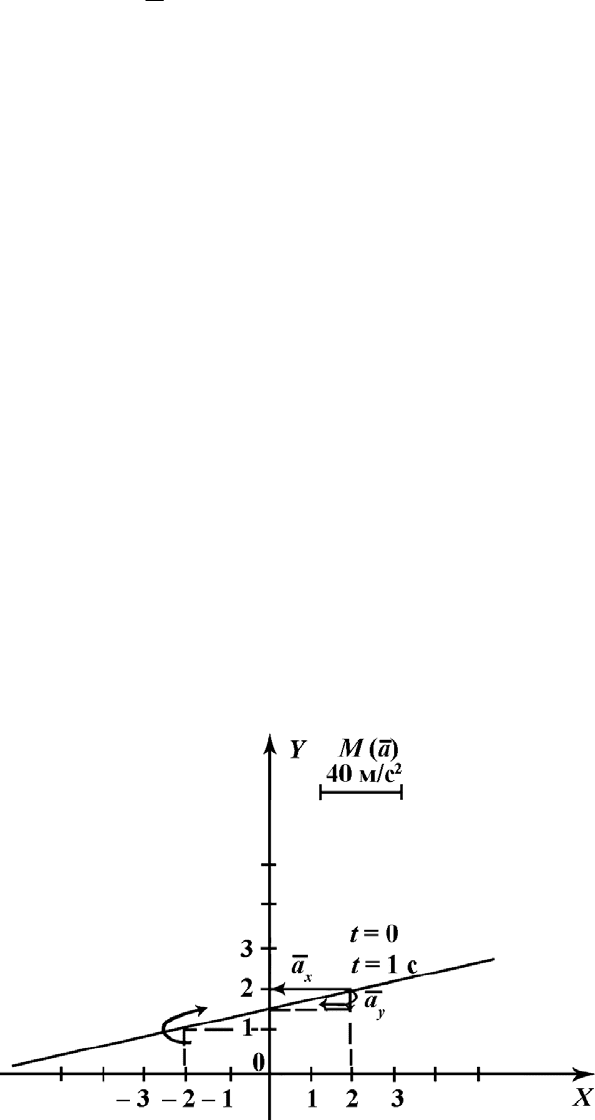
114

С другой стороны, имеем тригонометрическое тождество:

cos(2 ) 1 2sin ( )tt

=− π

Поэтому

12(2 )

y=− −

, или 46

− . (2)

Это выражение и является уравнением траектории точки.

Движение точки начинается в момент времени

= 0. В этот момент

2cos(2 ) 2cos0 2;

2sin( )2sin02 м.

=π==

⎧

⎪

⎨

=− π =− =

⎪

⎩

В момент времени t

= 1 c:

2cos(2 ) 2cos(2 ) 2м;

2sin( )2sin 2м.

=π=π=

⎧

⎪

⎨

=− π =− π=

⎪

⎩

То есть положение точки в моменты времени t

= 0 c и t

= 1 c совпадают.

С увеличением

t координаты точки изменяются периодически, с пе-

риодом

Т = 1 с и при всех изменениях t не могут выйти за пределы

2 м 2 м

−≤≤ ; 1 м 2 м.y

≤

≤ (3)

Поэтому траекторией точки является не вся прямая, описываемая

уравнением (2), а лишь ее отрезок, заключенный в указанных пределах (3).

С учетом этого выполним рисунок траектории точки и покажем на

нем ее положение в моменты времени

= 0 и t

= 1 с (рис. П.3)

Рис. П.3

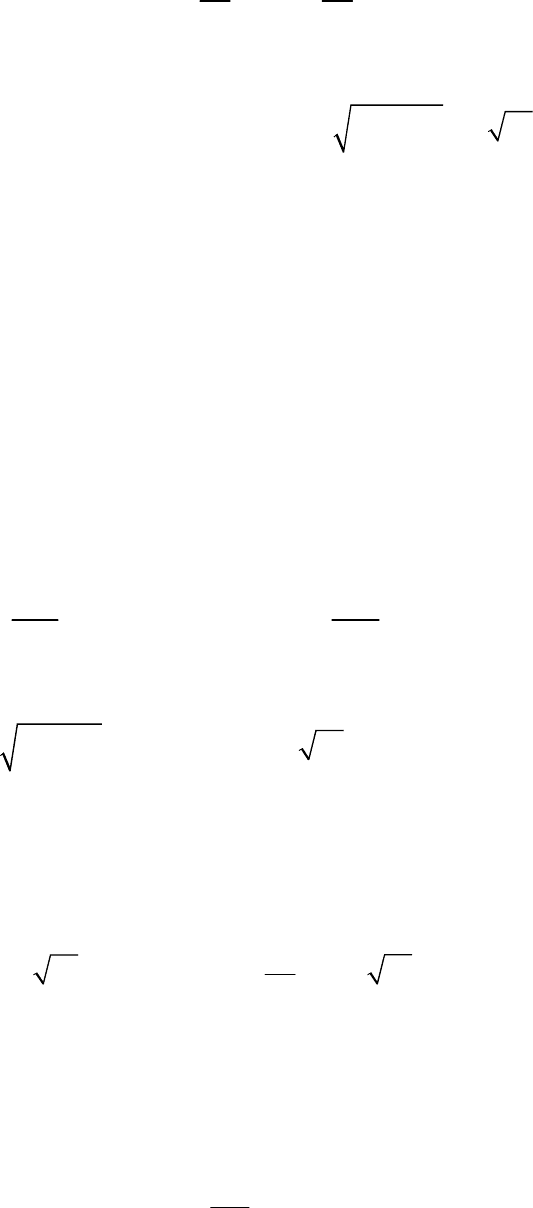
115

2. Определяем скорость точки. Ее проекции на оси координат опре-

деляются выражениями:

В нашем случае:

4sin(2 )

Vt=− π π ; sin(2 )

Vt=−π π ;

17 sin(2 )

VVV t

+=π π.

При t

= 0:

VV==, т. е. движение начинается без начальной

скорости.

При

= 1 с:

V = ;

Как отмечалось выше, координаты точки периодически меняются,

т. е. точка совершает колебательное движение по указанному отрезку пря-

мой. Периодически (через 1 с) происходят остановки точки, в эти моменты

происходит изменение направления движения на обратное. Моменты вре-

мени

= 0 и t

= 1 с как раз и относятся к ним.

Определяем ускорение точки.

При координатном способе задания движения точки вычисляются

проекцией вектора ускорения на координатные оси:

8cos(2)

==−π⋅ π

;

2cos(2)

=− π ⋅ π . (5)

Полное ускорение

22 2

2cos(2)1781,3cos(2)

aaa t t=+=π⋅π⋅≈⋅π. (6)

При t

= 1 с:

878,9(м/с );

a =− π ≈−

219,7(м/с );

a =− π ≈−

81,3(м/с ).a ≈

4. Касательные ускорение точки.

Так как

17 sin 2Vt=π π

, то

217cos2

=π π.

При t

= 1 с:

81,3(м/с ).aa

Данное выражение полностью совпадает с выражением (6), описываю-

щим полное ускорение точки, что вполне естественно, т. к. движение точки

происходит по прямой траектории (радиус кривизны прямой ρ=∞ и, следова-

тельно, нормальное ускорение

независимо от величины V).

116

В моменты времени, бесконечно близкие к t

, но предшествующие

ему, движение точки замедленное, а в моменты времени, бесконечно близ-

кие к t

, но после него – движение точки ускоренное.

4. Дуговая координата и путь, пройденный точкой.

Если принять:

1) начало отсчета дуговых координат S движущейся точки в том по-

ложении, где находилась точка в начальный момент времени t

= 0, т. е.

в точке с координатами (2; 2) на правом конце траектории (рис. П.4),

то S

= 0, при t

= 0;

Рис. П.4

2) направление отсчета положительных значений дуговых координат –

к левому концу траектории (это – вполне естественно);

3) путь, пройденный точкой к начальному моменту времени t

= 0,

равным нулю (S

= 0), то дуговая координата точки в произвольный мо-

мент времени будет вычисляться по формуле:

SVdt

⋅

∫

где V – скорость точки, изменяющаяся по закону (4΄). Получаем:

17 sin(2 ) cos(2 ) .

SVdt t tC=⋅= ⋅π⋅ π=− ⋅ π+

∫∫

В соответствии с принятыми оговорками (при t

= 0, S

= 0):

(м).

С =

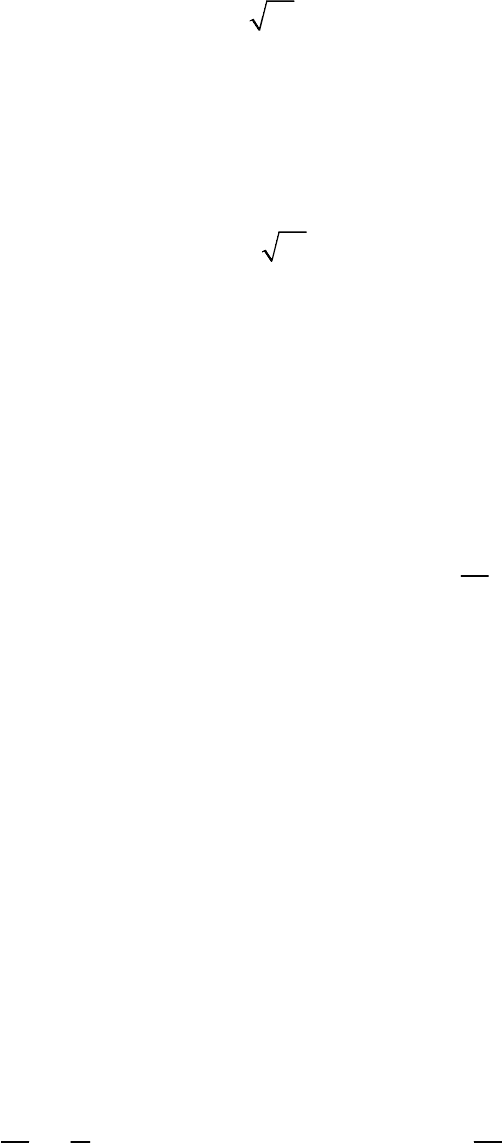
117

Следовательно,

0,5 17 (7 cos 2 ).St=⋅+π

Это – закон движения точки по траектории. Пользоваться им можно

только при выполнении условий, принятых выше (начало, направление отсчета S).

Чтобы получить формулу для вычисления пути найдем моменты

времени, когда происходят остановки точки. Из(4′) получаем:

017sin(2).t

π⋅ π

Отсюда моменты остановок: t

1ост

= 1,5 с; t

2ост

= 1 с; t

3ост

= 1,5 с и т. д.

С учетом принятой оговорки (S

= 0 при t

= 0) получаем: путь, прой-

денный точкой к произвольному моменту времени t: (пусть 1, 5 c 2 ct<< ).

Пример 3

Движение точки задано уравнениями (х, у – в см, t – в сек.):

4cos( ) 2;

t=π− 2sin( )

= (1)

Найти траекторию точки, выполнить ее рисунок и показать направ-

ление движения точки по траектории в различные моменты времени.

Для момента времени t

=1,5 с:

Вычислить положение точки и радиус кривизны траектории в этом

месте, скорость и ускорение, касательное нормальное ускорение точки.

Полученные результаты показать на рисунке траектории. Сделать

вывод о характере движения точки в момент t

Решение

Для получения уравнения траектории исключим время из заданных

уравнений движения, воспользовавшись тождеством:

cos 2 1 2sin

=− α

имеем:

sin

tyπ

⎛⎞

⎜⎟

⎝⎠

;

4cos( ) 2 41 2sin 2 2(1 ).

⎡π⎤

⎛⎞

=⋅ π−= − −= −

⎜⎟

⎢⎥

⎝⎠

⎣⎦

Итак, уравнение траектории

2(1 )

y=−. (2)

118

Это – уравнение параболы с горизонтальной осью симметрии, совпа-

дающей с осью ОХ. Но траекторией является только часть этой параболы,

ограниченной координатами

62,

22.

−

≤≤

⎧

⎨

−

≤≤

⎩

(3)

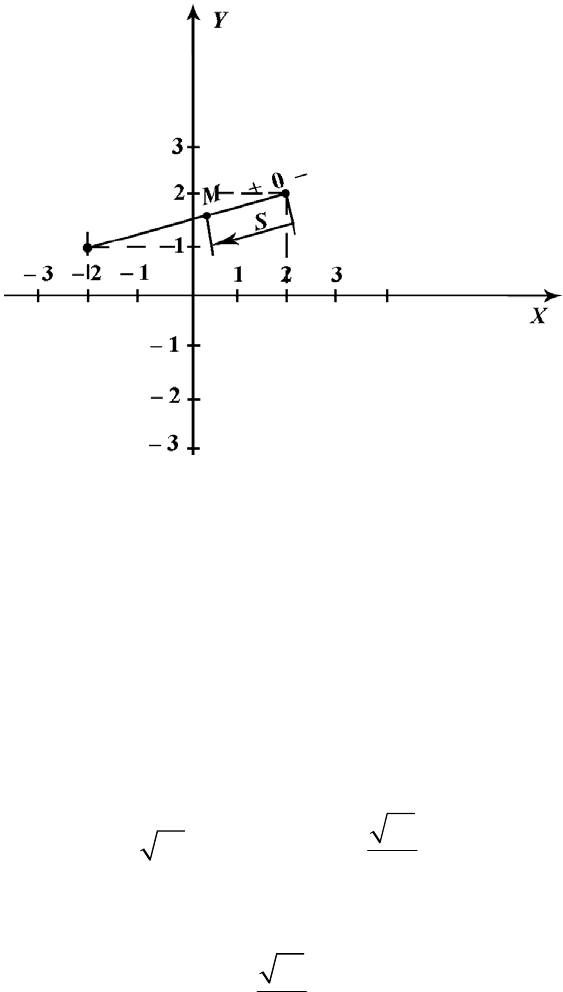
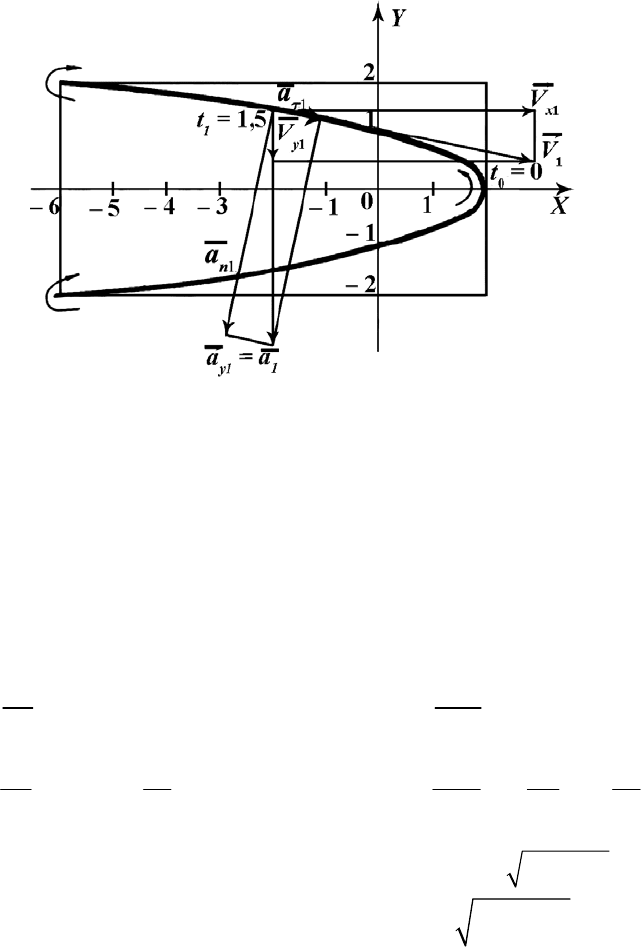
Выполняем рисунок траектории (рис. П.5).

Определим и покажем на нем положения точки в моменты времени

= 0 и

= 1,5 с:

=2 см; у

=0; х

= – 2 см; у

= 1,41 см.

Рис. П.5

Подставляя в исходные уравнения движения точки моменты времени

0, 1/6, 2/6, и т. д. до 2 с интервалом в 1/6 с вычисляем последовательные

положения точки на траектории и приходим к выводу, что точка совершает

колебания вдоль выделенной части параболы и ни при каких t не выходит

за пределы ограничений (3).

Определяем скорость и ускорение точки.

4sin();

==−π⋅π

4cos();

а t

=− π π

cos ;

dy t

⎛⎞

==π⋅

⎜⎟

⎝⎠

sin

⎛⎞

==−

⎜⎟

⎝⎠

При t

=1,5 с:

12,56 см/с;

V =

2,22 см/с;

−

111

12,76 см/с

VVV=+=

При t

=1,5 с:

a =

3, 49 см/с ;

a =−

22 2

111

3, 49 см/с

aaa=+=

119

Касательное и нормальное ускорение точки при t

=1,5 с:

11 11

0,607 см/с

xx yy

Va Va

;

22 2 2 2

3, 49 0,607 3,44 см/с .

aaa

=−= − =

Полученные результаты показываем на рисунке траектории точки.

Радиус кривизны траектории в точке (х

, у

12,76

47,2 см.

3, 44

ρ= = =

Движение точки в момент времени t

=1,5 с – ускоренное, так как на-

правления вектора скорости и вектора касательного ускорения совпадают

(рис. П.5).

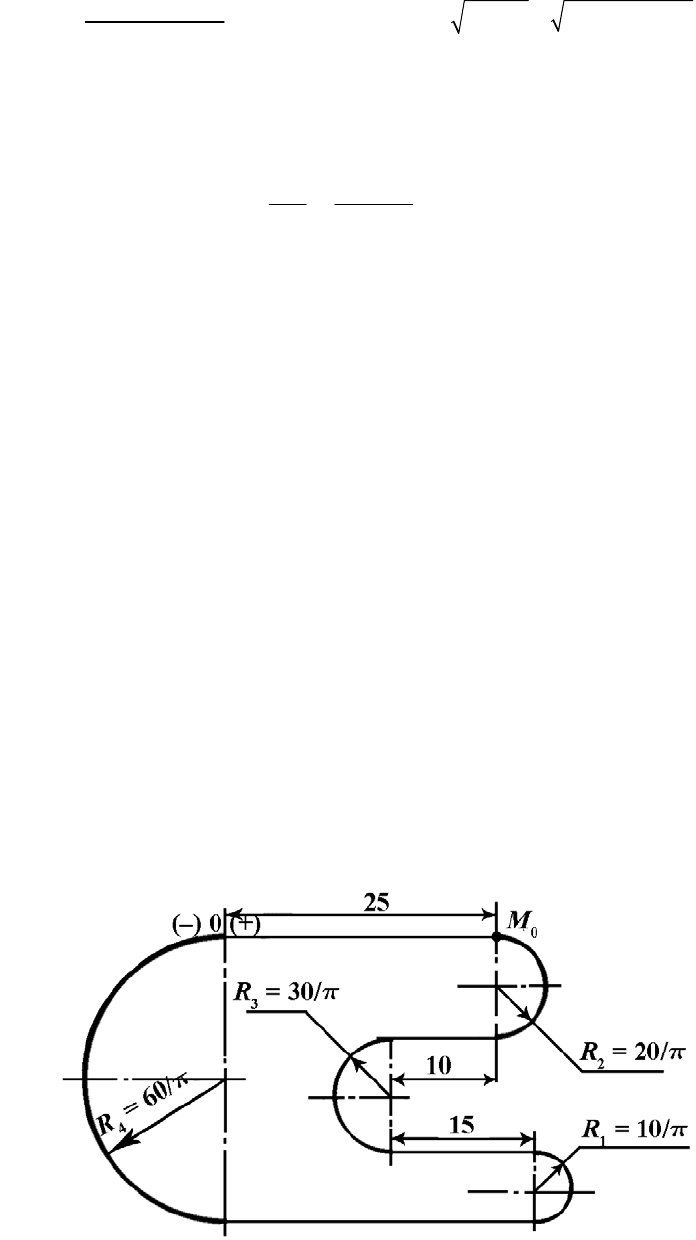
Пример 4

Движение точки М происходит по траектории, показанной на рис. П.6, а

согласно заданному графику изменения скорости (рис. П.6, б). Движение

точки начинается в момент времени t

= 0 из положения М

(ОМ

= 25 м).

Определить последовательные положения точки на траектории в вы-

деленные на рис. П.6, б моменты времени, описать основные особенности

движения точки и вычислить путь, пройденный точкой за промежуток

времени t

= 0 до t

= 12 с.

Решение

Выполняем в масштабе чертеж траектории точки в соответствии с

заданными размерами (рис. П.6, а). Определяем и показываем на чертеже

положения точки на траектории в моменты времени t

, …, t

Рис. П.6, а

а)

120

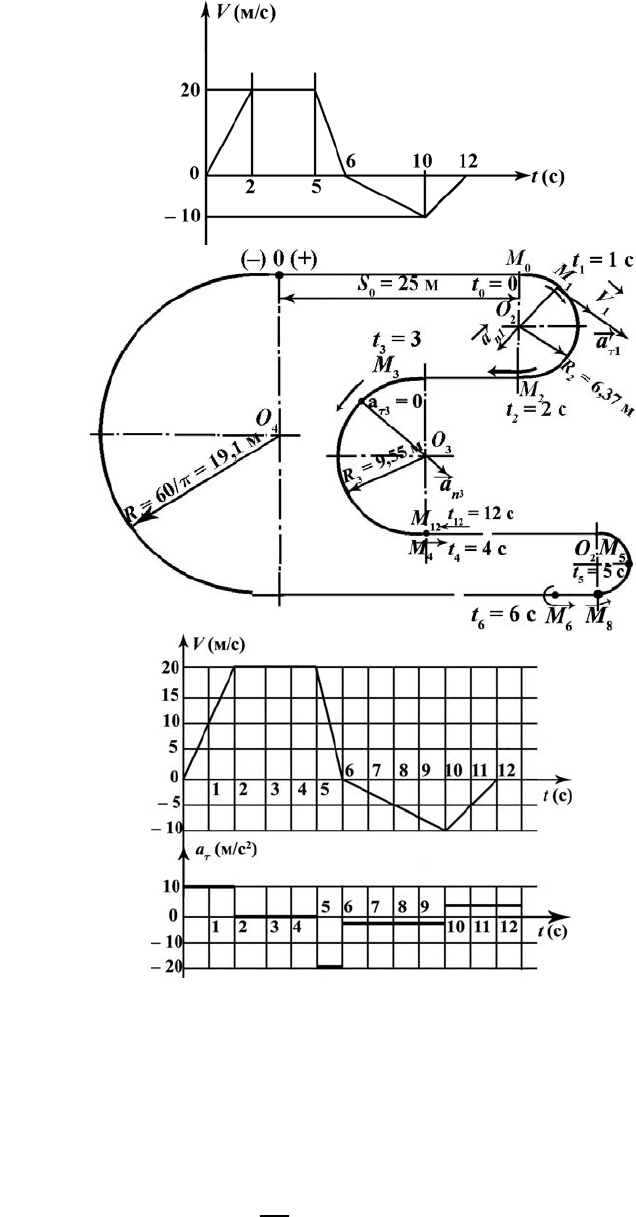
Рис. П.6 (б, в, г)

1. Дуговая координата и путь. Направление движения

Скорость V точки и закон ее движения по траектории, т. е. закон S = f(t)

изменения ее дуговых координат с течением времени, связаны зависимостями

= и

SS Vdt

+⋅

∫

где S

– значение дуговой координаты точки в начальный момент вре-

мени,

= ОМ

= 25 м.

б)

в)

г)