Захаров Н.М., Кулик Н. А Сборник задач по теоретической механике для контрольных и расчетно-графических работ
Подождите немного. Документ загружается.


31
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ С-1, С-2, С-3
Эти задачи относятся к теме «Произвольная плоская система сил».
Для их решения необходимо твёрдое знание следующих вопросов:
1)
проекция силы на ось (величина, знак);
2)
алгебраический момент относительно точки и его свойства;
3)
теорема Вариньона о моменте равнодействующей силы;
4)
алгебраический момент пары сил и его свойства;
5)
распределённые нагрузки и их равнодействующие.
В задачах на равновесие несвободного твёрдого тела дополнительно
надо знать вопросы:
1)
связи и их реакции, основные типы связей;
2)
условия и уравнения равновесия произвольной плоской системы
сил, различные формы уравнений равновесия.
Пример 1
Приведение произвольной плоской системы сил к простейшему виду
Систему сил, действующих на брус AB (рис. П.1), привести к про-
стейшему виду.
1
45кНF = ;
2
8кНF
=
; 40кН мm
=
⋅ ; 5кН/мq
=
;
2 (sin 2/ 5;cos 1/ 5).tgα= α= α=
На рисунке линейные размеры указаны в метрах.
Рис. П.1
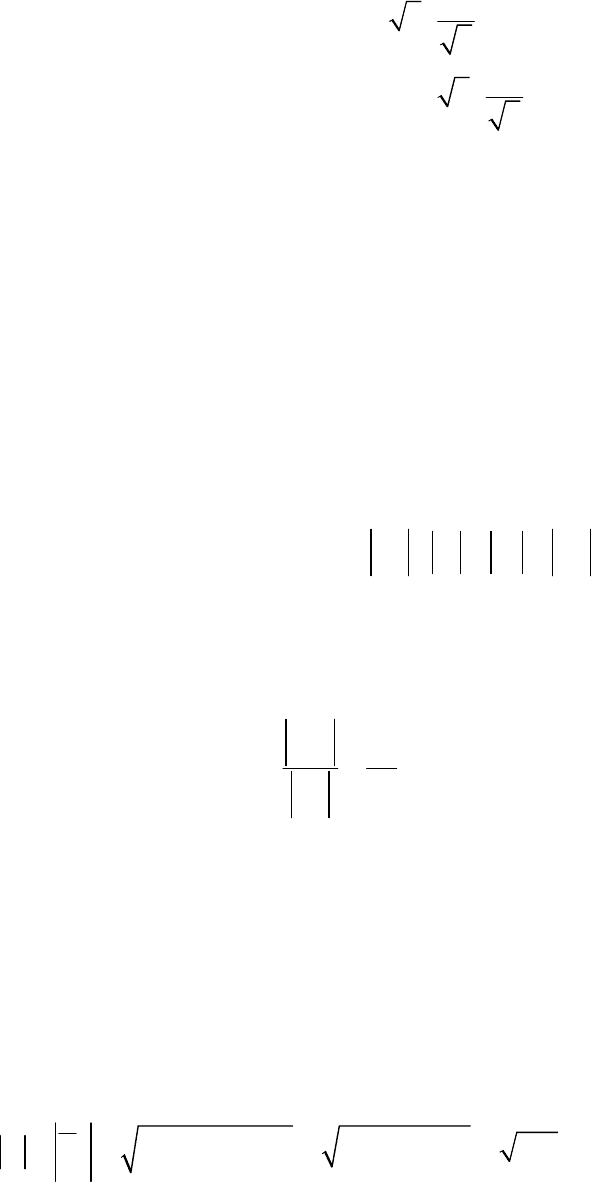
32
Решение
Примем в качестве центра приведения точку С (рис. П.2, а). Выберем
оси проекций X и Y. Проекция главного вектора исходной системы сил на
выбранные оси определяется:
1
1
cos 4 5 4кН.
5
xkx
RFF
∗
==α=⋅=
∑
21
2
sin 2 8 4 5 5 2 10кН.
5
yky
RFFF q
∗
= =− + α−⋅=−+ ⋅ −⋅=−
∑
Главный момент заданной системы сил относительно принятого цен-
тра приведения С:
(
)
2
4 26 84 40 526 68 кН м.
Cck
MmFFmq
∗
= = ⋅− −⋅⋅=⋅− −⋅⋅=− ⋅
∑
Полученный результат (с учётом знаков этих алгебраических вели-
чин, т. е. истинные направления главного вектора и главного момента) по-
казываем на рисунке (рис. П.2, б).
Так как
*
0
R
≠
, то полученная система сил
(
)
**
,
C
RM может быть
упрощена и заменена одной силой (т. е. исходная система сил имеет рав-
нодействующую). Чтобы получить её, представим главный момент
*
C
M
в
виде пары сил
(
)
12
, PP
, приняв
12 Y
PP R
∗
==
;
12 Y
PP R
∗
==
.
Приложим одну из сил пары (например,
1
P
) в точке С и направим её
противоположно силе
*
Y
R
(рис. П.2, в). Другая сила этой пары пройдёт че-
рез некоторую точку D бруса, удалённую от этой точки С на расстояние
*
*
68
6,8 м.
10
C
Y
M
hCD
R
== ==
Положение точки D найдём из условия совпадения направления
*
C
M
и момента пары
(
)
12
, PP
. То есть точка D располагается правее точки С
(см. рис. П.2, в). Далее, уравновешивающиеся силы
1
P
и
*
Y
R
исключаем из
рассмотрения, а силу
*
X
R
переносим из точки С в точку D по линии ее дей-
ствия (рис. П.2, г). Наконец, сложив силы
2
P
и
*
X
R
, получаем равнодейст-
вующую силу
R
(4; –10) исходной системы сил.
222 2
( ) ( ) 4 ( 10) 116 10,8 H.
xy
RR R R
∗
∗∗
== + = +− = =

33
Рис. П.2
Пример 2
Определение опорных реакций балки
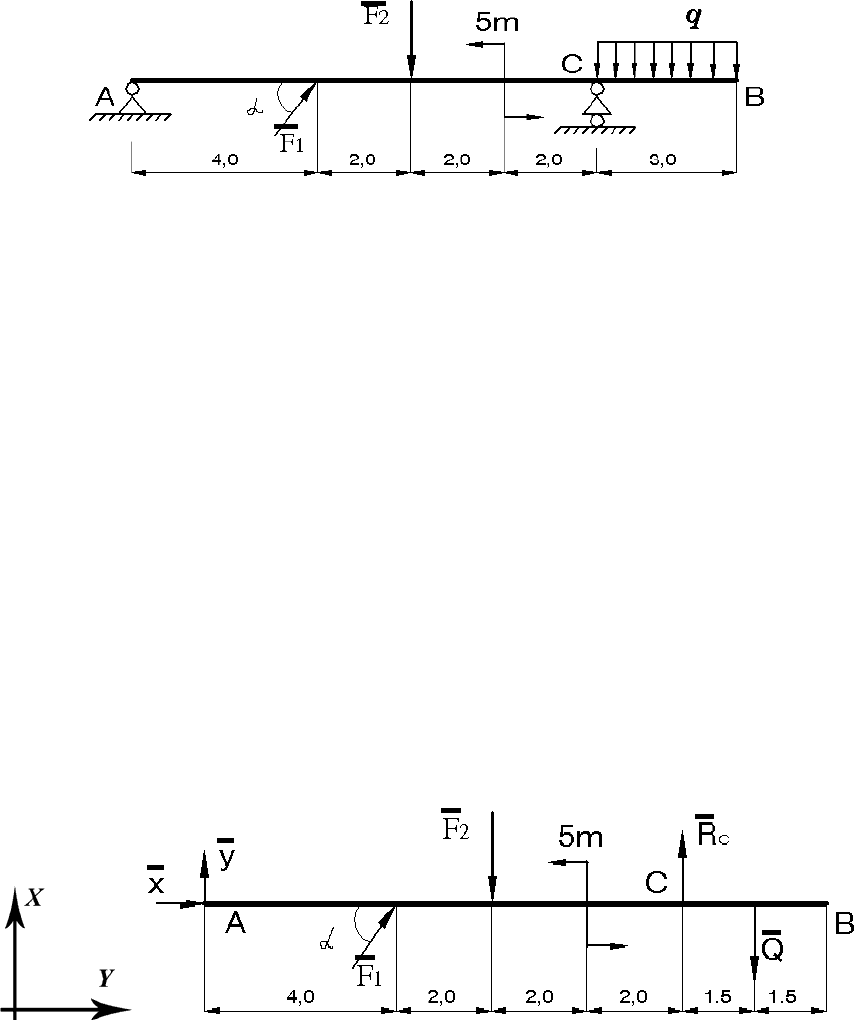
Балка АВ, нагруженная произвольной плоской системой сил, удер-
живается в равновесии при помощи неподвижной шарнирной опоры А и
подвижной шарнирной опорой С (рис. П.3). Определить их реакции, если:
F
1
= 12 кН; F
2
= 10 кН; m = 4 кН⋅м; q = 6 кН/м; α = 30°. Линейные размеры
на рисунке даны в метрах.
R
R
)
34
Рис. П.3
Решение
Для определения реакций опор рассмотрим равновесие балки АВ. Ре-
акция
c
R
горизонтально-подвижной шарнирной опоры С направлена вер-
тикально (предположим вверх). Реакцию
А
R
неподвижной шарнирной
опоры А представим в виде двух составляющих
А
Х
и
A
Y
, направленных
горизонтально и вертикально (например, вправо и вверх). Мысленно заме-
ним опоры этими силами реакций и сделаем балку свободной (принцип
освобождаемости от связи). Равномерно распределённую нагрузку интен-
сивности q, равную 6 кН/м, заменим равнодействующей силой
36318 кН.Qq
=
⋅=⋅=
Линия действия силы Q
проходит через середину участка длинной
3 м, где эта нагрузка действует. Так получается расчётная схема несвобод-
ной балки (рис. П.4), находящейся в равновесии под действием произволь-
ной системы сил.
Рис. П.4
Выбрав оси проекций Х и Y, составляем и решаем уравнения равно-
весия балки:
1) 0
KX
F =
∑
:
1
cos30 0
A
XF
°
+=; 12 0,865 0
A
X
+
⋅=; 10,4 кН
A
X =− .
Знак «–» указывает на то, что эта составляющая силы реакции
А
R
на-
правлена в противоположную сторону, т. е. не вправо, как предполагали вна-
чале, а влево. Чтобы не исправлять решение, оставим без изменения выпол-
ненный ранее рисунок расчётной схемы балки, но будем иметь в виду, что
10,4 кН
A
X =−
.
A
A

35
2)
0
KY
F =
∑
:
12
sin 0
AC
YF FRQ+⋅ α− + −=
;
12 0,5 10 18 0
AC
YR+⋅ −+ −=
;
22 кН
AC
YR
+
=
3)
(
)
0
Ak
mF=
∑
:
12
sin 4 6 5 10 11,5 0
C
FFmRQ⋅α⋅−⋅+ +⋅−⋅ =;
12 0,5 4 10 6 5 4 18 11,5 0
C
R⋅⋅−⋅+⋅+−⋅ =
;
24 60 20 10 207 0
C
R
−
++⋅− =
; 22,3 кН
C
R =
Возвращаясь ко второму уравнению равновесия, вычисляем Y
A
:
22,3 22
A
Y +=; 0,3 кН
A
Y
=
− .
Истинное направление этой составляющей силы реакций
А
R
–
вертикально вниз. Полная реакция опоры А:
22 2 2
10, 4 0,3 10,5 кН.
AAA
Rxy=+= +=
Выполним проверку правильности решения задачи. Для этого соста-
вим ещё одно уравнение равновесия балки, причём такое, которое не ис-
пользовалось при определении сил реакций, например:
()
0
Bk
mF=
∑
:
12
13 sin 9 7 5 3 1,5 0.
AC
YF FmRQ−⋅−⋅ α⋅+ ⋅+ − ⋅+⋅ =
Подставим в это уравнение заданные и найденные силы, получаем:
( 0,3) 13 12 0,5 9 10 7 5 4 22,3 3 18 1,5 0−− ⋅ − ⋅ ⋅ + ⋅ + ⋅ − ⋅ + ⋅ = ;
3,954702066,9270−++− +=; 117 117 0
−
+=; 0 0.=
Следовательно, неизвестные силы реакций опор определены верно.
10,4 кН, влево
A
X =
; 0,3 кН, вниз
A
Y =
; 22,3 кН, вверх.
C
R =
Пример 3
Определение опорных реакций балки
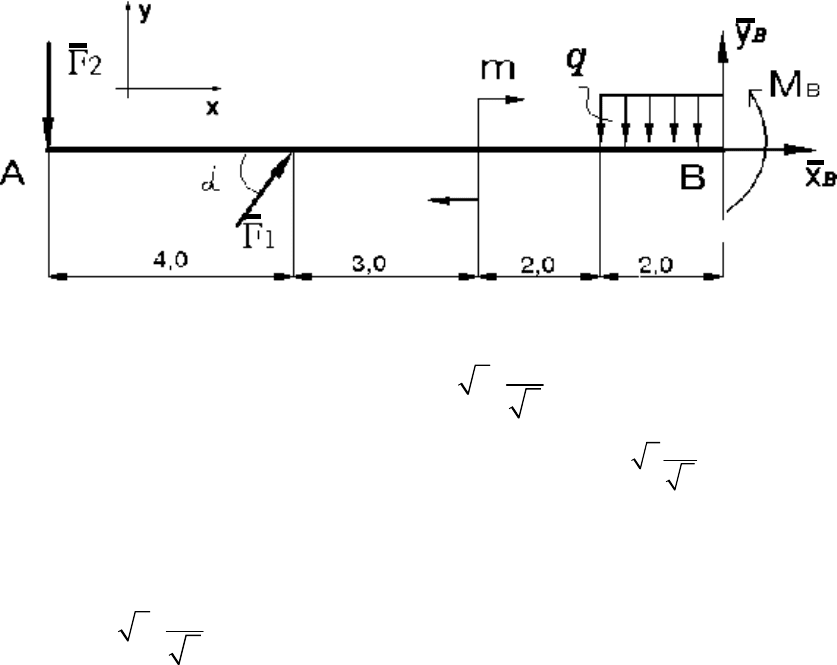
Брус, рассмотренный в примере 1, жёстко закреплён правым концом
(рис. П.5). Определить реакций этой связи и выполнить проверку правиль-
ности решения.
Дано:
F
1
= 45 кН ; F
2
= 8 кН;
m = 30 кН⋅м; q = 6 кН/м;
tgα = 2; (sinα =
2
5
;
cosα =
1
5
).
Рис. П.5
36
Решение
Брус, работающий на изгиб, называется балкой. Рассмотрим её рав-
новесие под действием заданной системы сил и искомых реакций жёсткой
заделки В. Эти реакции представим в виде неизвестной реактивной силы
B
R
(которую сразу разложим на две составляющие, параллельные произ-
вольно выбранным осям проекций Х и Y) и реактивного момента M
В
, вы-
брав его направление произвольно (например, против хода часовой стрелки).
Заменив жёсткую заделку В этими реакциями, получаем расчётную схему
балки в виде свободного твёрдого тела, находящегося в равновесии под
действием указанных сил и неизвестных сил (рис. П.6). Составляем и ре-
шаем уравнения равновесия балки.
Рис. П.6
1) 0
KY
F =
∑
:
1
cos 0
B
FX⋅α+ =;
1
45 0
5
B
X
⋅
+=
; 4 кН
B
X =−
2)
0
KY
F =
∑
:
21
sin 2 0
B
FF q Y−+⋅ α−⋅+ =
;
2
845 52 0
5
B
Y
−
+−⋅+=
;
10 кН.
B
Y
=
3)
()
0
Bk
mF=
∑
:
21
11 sin 7 2 1 0
B
FF mq M⋅− α⋅−+⋅⋅+ =;
2
811 4 5 7 30 521 0
5
B
M⋅− ⋅ ⋅− +⋅⋅+ =
; 88 56 30 10 0
B
M
−
−++ =;
12 кН м.
B
M
=
−⋅
Знак «–» при M
B
указывает на то, что истинное направление реактивно-
го момента противоположно предварительно принятому: т. е. M
B
= 12 кН⋅м;
направление – по ходу часовой стрелки.
Чтобы не проводить всё решение заново, оставим принятые направ-
ления реакций жёсткой заделки В без изменения, но будем помнить о зна-
ках найденных реакций.
37
В заключение выполним проверку правильности решения задачи,
составим ещё одно уравнение равновесия. Например:
0
A
m
=
∑
:
1
sin 4 2 10 11 0
BB
FmqYMα⋅ − − ⋅ ⋅ + ⋅ + =
;
2
45 43052101011(12)0
5
⋅⋅−−⋅⋅+⋅+−=
; 32 30 100 110 12 0
−
−+−=; 0 0.
=
Полученное тождество свидетельствует о правильности решения задачи.
X
B
= 4 кН (влево); Y
B
= 10 кН (вверх); M
B
= 12 кН⋅м (по ходу часовой стрелки).
Пример 4
Определение опорных реакций рамы
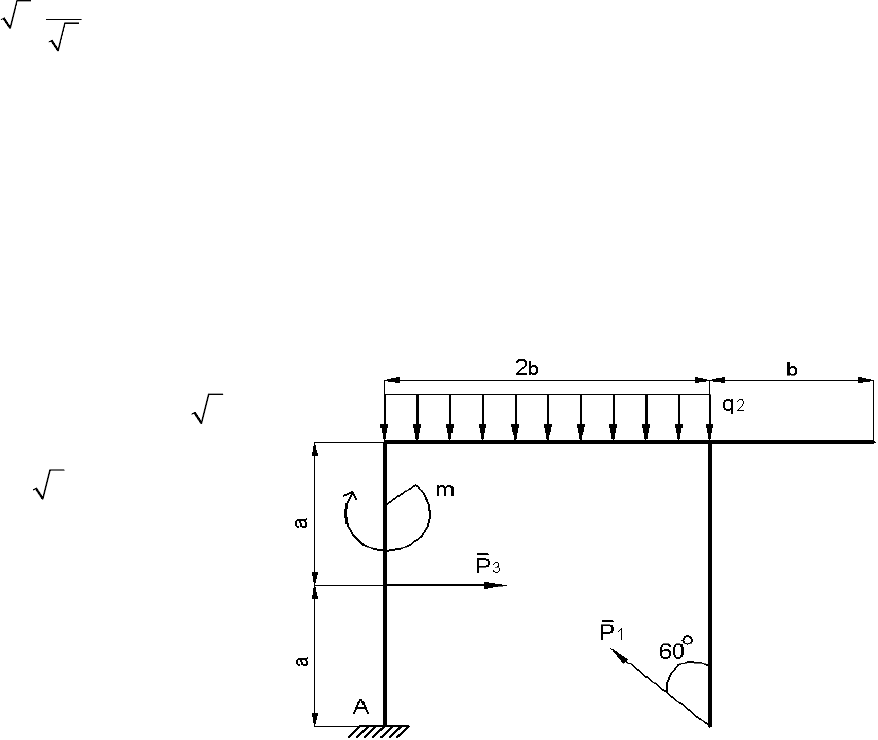
Плоская рама находится в равновесии благодаря наложенной связи –
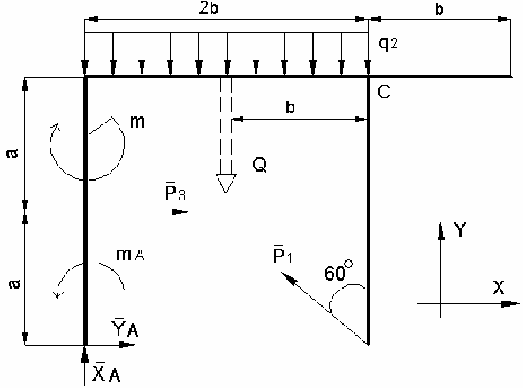
жесткой заделке в сечении А (рис. П.7). Определить реакции связи и
выполнить проверку правильности решения.
Дано:
Р
1
= 24 кН; Р
3
= 12 3 кН;
q
2
= 3 кН/м; m = 18 кН⋅м;
а =
3 м; b = 3 м.
Рис. П.7
Решение
Для определения реакций жесткой заделки в точке А рассмотрим
равновесие рамы, находящейся под действием произвольной плоской сис-
темы сил. Заменим жесткую заделку искомыми реакциями: X
А
, Y
А
, m
А
,
а распределенную нагрузку – ее равнодействующей:
2
2 323 18 кН.Qq b=⋅=⋅⋅=
Получаем расчетную схему рамы в виде свободного твердого тела,
находящегося в равновесии под действием заданной произвольной пло-
ской системы сил и произвольной плоской системы сил реакций, заме-
няющих жесткую заделку А (рис. П.8).
38
Рис. П.8
Выбираем оси проекций Х и У, составляем уравнения равновесия тела:
1) 0
KY
F =
∑
:
13
sin 60 0
A
XP P−⋅ °+ =.
2) 0
KY
F =
∑
:
1
cos 60 0
A
YQP−+⋅ °=.
3) 0
A
m =
∑
:
13
cos 60 2 0.
A
mmQbP bPa−−⋅+ °⋅ −⋅=
Подставив значения заданных величин и решив уравнения, получаем:
X
A
= 0; Y
A
= 0; m
A
= 36 кН⋅м.
Для проверки составим еще одно уравнение равновесия, не исполь-
зованное при решении:
(
)
0
Ck
mF
=
∑
31
22 sin6020
AA A
mX aYbmQbPaP a+⋅−⋅−+⋅+⋅−⋅ °⋅=
Подстановка полученных и заданных величин в это уравнение приводит
к тождеству 0 = 0. Следовательно, неизвестные силы реакций найдены верно.
Пример 5
Определение опорных реакций рамы
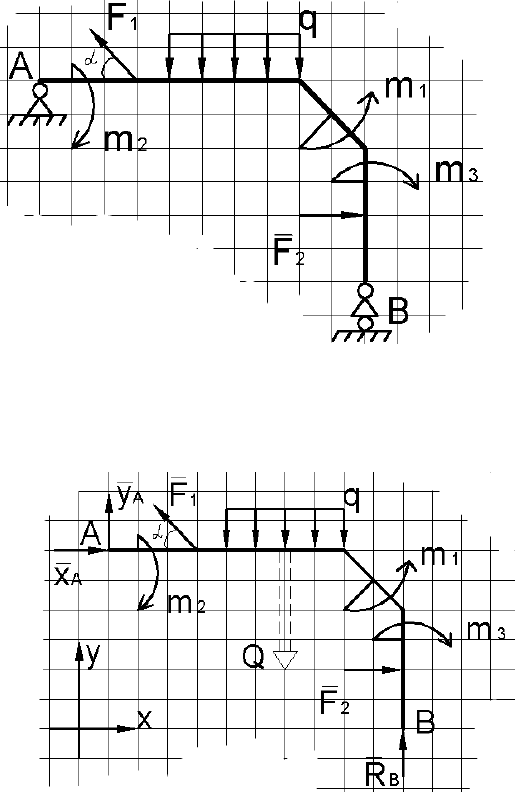
Плоская рама находится в равновесии под действием произвольной
плоской системы сил и закреплена неподвижно при помощи неподвижной
шарнирной опоры (точка А) и подвижной шарнирной опоры (точка В).
Приняв линейные размеры рамы непосредственно из рис. П.9, определить
реакции опор рамы и выполнить проверку правильности решения задачи.
39
Дано:
sinα = 0,8; cosα = 0,6; F
1
= 50 кН;
F
2
= 30 кН; q = 10 кН/м;
m
1
= 100 кН⋅м; m
2
= 60 кН⋅м;
m
3
= 40 кН⋅м.
Рис. П.9
Решение
Для определения реакций
связей рассмотрим равновесие
рамы. Чтобы получить расчет-
ную схему, отбросим связи и за-
меним их действие искомыми
силами реакций. Реакцию опоры
в точке А представим в виде двух
составляющих
A
X
и
A
Y
, направ-
ленных параллельно произвольно
принимаемым осям проекций Х и
Y (рис. П.10).
Рис. П.10
Реакция
B
R
подвижной шарнирной опоры в точке В направлена пер-
пендикулярно опорной поверхности, т. е. вертикально (например, вверх).
Равномерно распределенную нагрузку интенсивности q = 10 кН/м заменим
ее равнодействующей силой
440 кН.Qq
=
⋅=
Линия действия этой силы проходит через середину участка длиной
4 м, на который действует нагрузка.
Полученная расчетная схема представлена на рис. П.10.
Составляем и решаем уравнения равновесия произвольной плоской
системы сил, действующей на раму:
1)
0
KY
F =
∑
:
12
cos 0
A
XF F−⋅ α+ =
;
50 0,6 30 0
A
X
−
⋅+=
;
0
A
X =
.
2)
()
0
Ak
mF=
∑
:
21 1 3 2
sin 3 6 10 4 0
B
mF Q mmR F−+⋅α⋅−⋅+−+ ⋅+⋅=;
80 50 0,8 3 40 6 100 40 10 30 4 0
B
R−+⋅ ⋅− ⋅+ − + ⋅+⋅=; 2 кН
B
R = .
40
3)
()
0
Bk
mF=
∑
:
11 2132
610cos6sin74 20;
AA
XY F F QmmmF−⋅−⋅+⋅α⋅−⋅α⋅+⋅−+−−⋅=
0 0 50 0,6 6 50 0,8 7 40 4 80 100 40 30 2 0
A
Y−− ⋅+ ⋅ ⋅− ⋅ ⋅+ ⋅− + − − ⋅=;
2 кН
A
Y =− .
Выполним проверку правильности полученных результатов, соста-
вив еще одно уравнение равновесия рамы. Например:
0
KY
F =
∑
:
1
sin 0
AB
YF QR
−
⋅α−+ =; 2500,84020
−
+⋅ −+=; 00.=
Значит реакции опор рамы найдены верно.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ С-4, С-5, С-6, С-7
Эти задачи – на равновесие системы сочлененных тел. В них впервые
ставится вопрос об определении внутренних сил, действующих между со-
ставными частями конструкции.
Следует иметь в виду, что внутренние силы есть во всех телах, во
всех системах, в любых конструкциях. Но они, подчиняясь принципу ра-
венства действия и противодействия, существуют всегда попарно
. Поэтому
в любом теле, в любой системе, в любой конструкции они между собой
уравновешиваются. По этой причине при рассмотрении равновесия тела,
системы или конструкции в целом эти внутренние силы не вводятся в
уравнения равновесия. Но их знание необходимо для создания прочных,
работоспособных конструкций, механизмов и т. п. Кроме того, без
опреде-
ления этих сил не всегда удается решить задачи о нахождении сил реакций
внешних связей методами теоретической механики.
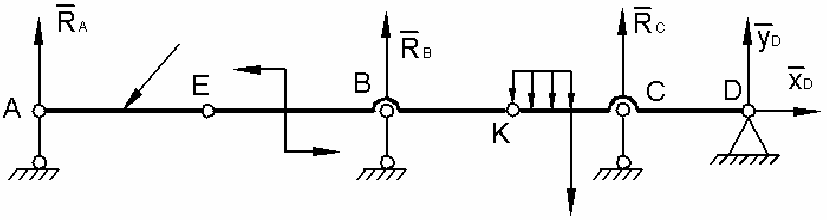
Например, конструкция, показанная на рис. П.11, состоит из трех тел
(балок
АЕ, ЕК, КD), соединенных между собой шарнирами Е и К.
Рис. П.11
Для удержания ее в равновесии нужны внешние связи. В рассматри-
ваемой конструкции таковыми являются опорные стержни в точках
А, В, С
и неподвижная шарнирная опора D. Под действием внешних заданных на-
грузок в них (опорах) появляются неизвестные силы реакций общим числом 5
