Юнин Е.К. Введение в механику глубокого бурения
Подождите немного. Документ загружается.

51
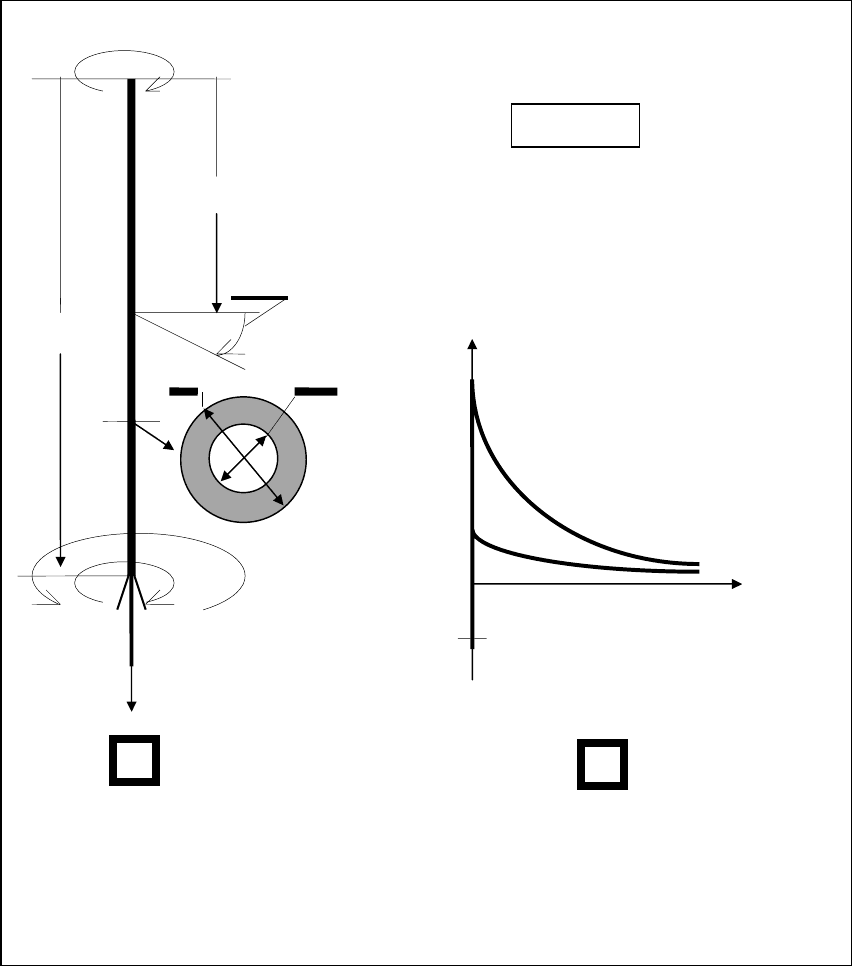
ния вращению долота М
Н
по мере увеличения скорости его вращения при по-
стоянной осевой нагрузке. Кроме этого возрастание осевой нагрузки увеличива-
ет момент сопротивления вращению долота. Качественная картина изменения
М
Н
от n, показанная на рис.3.1, поз.2, характерна для всех без исключения типов
породоразрушающего инструмента. В дальнейшем мы будем предполагать, что
эта зависимость нам известна.
0 п
0
Р
1
< Р
2
x
ϕ
(x,t)
H M
H
D d
A A
Р
2
п
Н
Р
1
M
H
0 п
0
Р
x
1 2
Рис.3.1
52
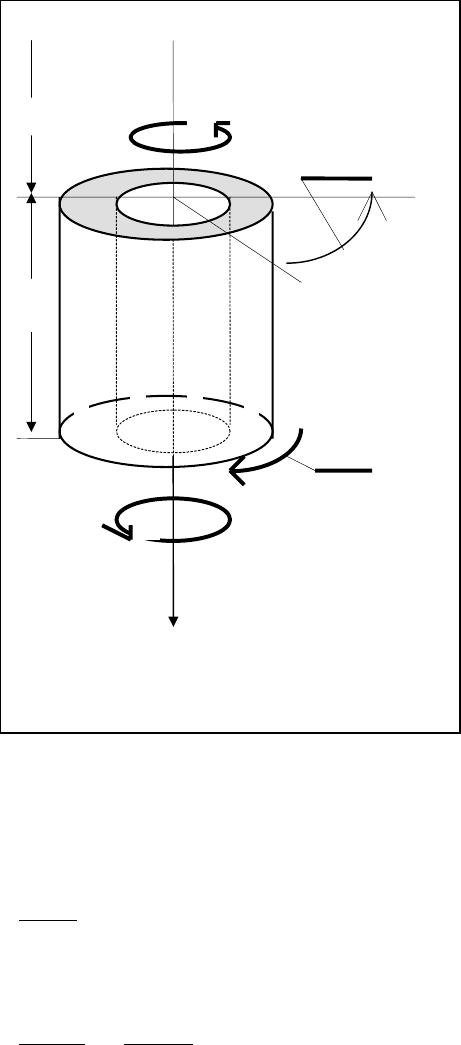
Выделим на расстоянии х от
верхнего торца малый элемент
стержня длиной ∆x и обозначим
через f
τ
величину момента сопро-
тивления вращению бурильной ко-
лонны из-за ее трения о стенки
скважины и взаимодействия с бу-
ровым раствором, приходящейся на
единицу длины колонны (рис.3.2).
Тогда на выделенный элемент дей-
ствует момент сопротивления вра-
щению f
τ
∆x. Составим уравнение
равновесия элемента при его рав-
номерном вращении. Поскольку
разность действующих в противо-
положных торцах крутящих мо-
ментов M(x+∆x) и M(x) должна
уравновешиваться моментом f
τ
∆x,
то имеем, что
M(x)
x
ϕ
(x)
∆x
f
τ
∆x
M(x+∆x)
x
Рис.3.2
Мх х Мх f х()()
+
−
≈
∆
∆
τ
.
Поделив левую и правую части полученного равенства на длину элемента ∆x
и устремив его к нулю, найдем:
dM
dx
f=
τ
.
(3.1.1)
Подставив сюда значение М(х) согласно выражению (2.2.3), получим:
d
dx
f
GJ
P
2
2
ϕ
τ
= .
(3.1.2)
Уравнение (3.1.2) описывает изменение угла поворота текущего поперечного
сечения бурильной колонны в зависимости от его координаты х при равномер-
ном вращении.
Рассмотрим равномерное установившееся вращение бурильной колонны с
угловой скоростью n
(осевую нагрузку P считаем постоянной во времени). Оче-
53
видно, что в данном случае угол поворота произвольного сечения бурильной
колонны имеет вид:
ϕ
=
n
t +
ϕ
0
(x).
Записанное равенство означает, что произвольное поперечное сечение вра-
щается с постоянной угловой скоростью n, но сами сечения повернуты относи-
тельно сечения в начале координат (х=0) из-за подкручивания колонны силами
сопротивления вращению на некоторые углы
ϕ
0
(
х
)
, зависящие от текущей ко-
ординаты поперечного сечения х. Подставив теперь значение
ϕ
в записанные
выше уравнение (с учетом того, что время t от координаты х не зависит), полу-
чим:
.
GJ
f
dx
)x(d
P
τ
ϕ
=
2
0
2
(3.1.3)
Граничные условия: 1. х= 0:
ϕ
0
= 0;
2. х=Н
:
GJ
d
dx
MPn
PH
ϕ
=− (,).
Первое граничное условие говорит о равенстве нулю относительного пово-
рота верхнего сечения (этот факт очевиден), а второе - о равенстве момента в
нижнем сечении стержня моменту сопротивления вращению долота со стороны
забоя (знак «минус» указывает на противоположные направления действий этих
моментов).
Предположим, что параметр f
τ
постоянен по длине бурильной колонны. То-
гда записанная задача (3.1.3) легко решается, и для величины
ϕ
0
(х) получаем:
(
.),(
2
11
)(
2
0
⎟
⎠
⎞
⎜
⎝
⎛
+−= xnPMHfxf
GJ
x
H
P
ττ
ϕ
)
(3.1.4)
Крутящий же момент, действующий в произвольном сечении колонны, за-
пишется согласно (2.2.3) после подстановки
ϕ
=
ϕ
0
(х) :
).n,P(М)Hx(f)x(М
H
−
−
=
τ
(3.1.5)
Подставив теперь в уравнение (3.1.4) значение х=Н, получим угол закручи-
вания нижнего торца бурильной колонны (забой) относительно верхнего (устье
скважины):
.),(
2
)(
0
⎟
⎠
⎞
⎜
⎝
⎛
+−= nPM
Hf
GJ
H
H
H
P
τ
ϕ
(3.1.6)

54
Знак «минус» указывает на отставание угла закручивания нижнего торца по от-
ношению к верхнему.
При х=0 соотношение (3.1.5) дает значение крутящего момента М(0), кото-
рый необходим для вращения колонны в скважине. Его абсолютная величина
М
0
=|М(0)| равна:
М f НМРп
Н0
=
+
τ
(,).
(3.1.7)
Заметим, что при отсутствии контакта породоразрушающего инструмента с
забоем (бурильная колонна находится в подвешенном состоянии) момент
М
Н
(Р=0,п)=0, а тогда при известном значении М
0
в верхнем сечении (ротор) и
известной глубине скважины формула (3.1.7) позволяет оценить величину па-
раметра f
τ
:
f
М
Н
τ
=
0
.
(3.1.8)
Очевидно, что крутящий момент создает в поперечном сечении бурильной
колонны касательные напряжения
τ
. Произведем их оценку.
Согласно (2.2.1) и (2.2.2) имеем:
τ
= Gr
d
dx
ϕ
.
Отсюда очевидно, что максимальное касательное напряжение
τ
max
будет равно:
.
dx
dGD
max
ϕ
τ
2
=
В силу равенства
d
dx
d
dx
ϕ
ϕ
=
0
согласно (3.1.4) получаем:
(
,)n,P(M)Hx(f
W
)x(
H
P
max
−−=
τ
τ
1
)
(3.1.9)
где W
P
называется полярным моментом сопротивления и вычисляется со-
гласно формуле:
W
J
D
P
P
=
2
.
(3.1.10)
3.2. Продольное движение бурильной колонны
55
Обратимся к математической модели, описывающей продольное перемеще-
ние бурильной колонны в вертикальной скважине, и выявим граничные условия
на забое и на устье скважины.
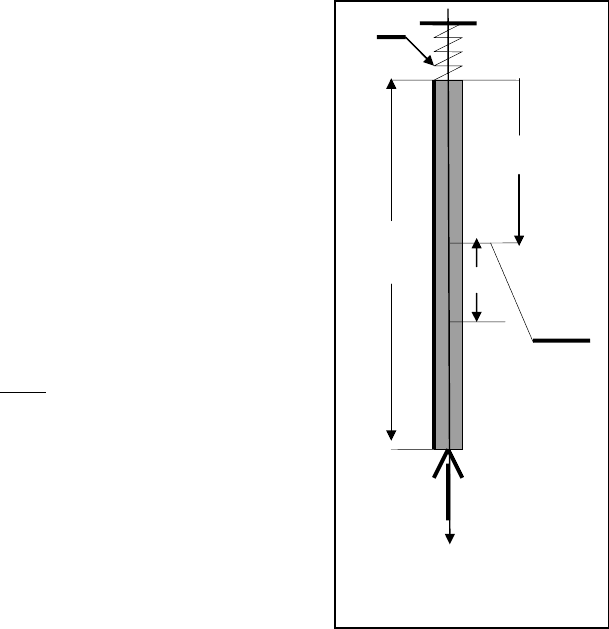
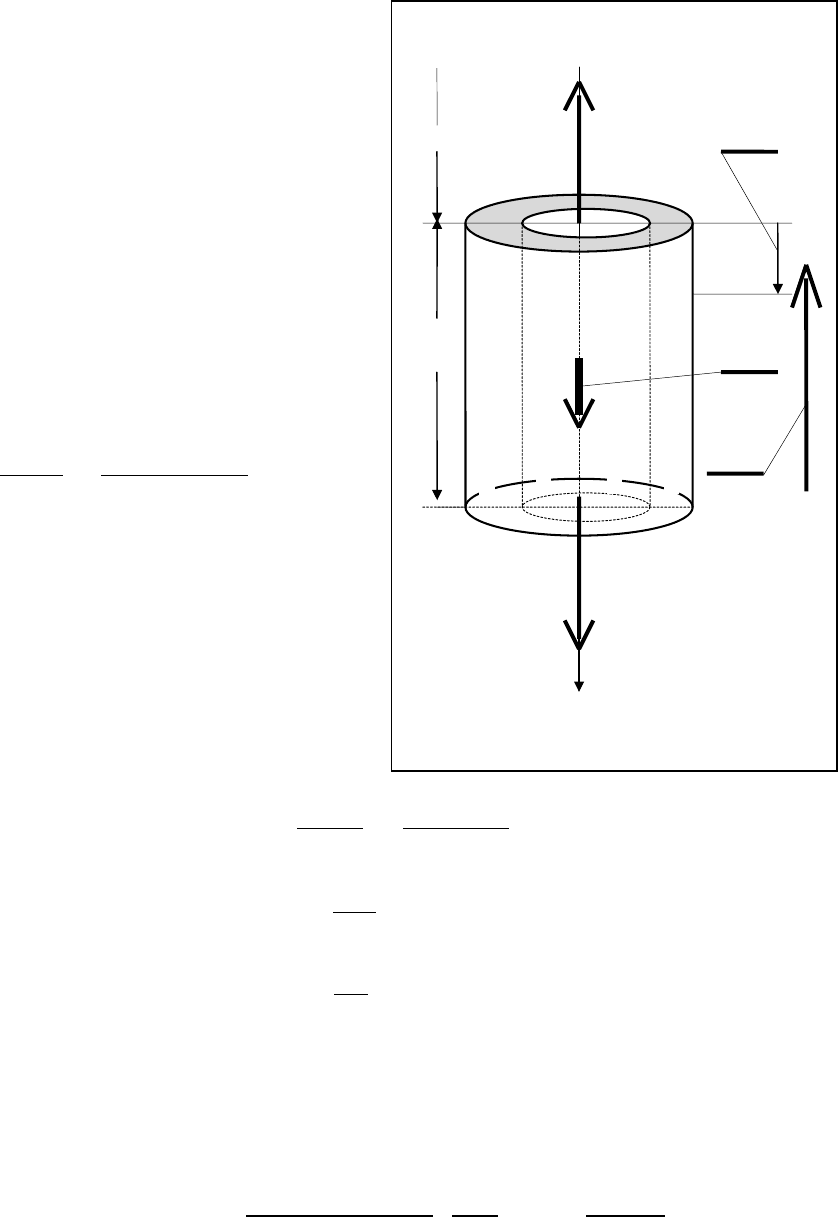
На рис.3.3 показана расчетная схема продольного
перемещения u(x,t) произвольного поперечного сече-
ния бурильной колонны. Координатная ось 0х на-
правлена от устья скважины к забою. Глубина сква-
жины равна Н. К нижнему торцу со стороны забоя
приложена сила Р (осевая нагрузка на долото). Оче-
видно, что согласно соотношению (2.1.4) граничное
условие на забое скважины может быть представлено
в виде:
c
0
x
H
∆
х
u(x)
х=Н :
EF
du
dx
P=− .
(3.2.1)
Знак «минус» перед силой Р взят потому, что ее
направление противоположно направлению коорди-
натной оси 0х. Верхний же торец бурильной колонны
(координата х=0) считаем закрепленным упруго (та-
левую систему с буровой вышкой заменяем условной
пружиной с коэффициентом упругости с). Рассмотрим более подробно краевое
условие на устье скважины.
P
x
Рис.3.3
Очевидно
, что коэффициент с определяется упругостью талевой системы и
буровой вышки. Рассмотрим вначале талевую систему.
На рис.3.4 приведена схема талевой системы, где l
0
- длина ветви талевого
каната; E
T
и F
T
- соответственно модуль Юнга материала талевого каната и
площадь его поперечного сечения; S
0
- расстояние от точки закрепления непод-
вижного конца талевой системы до оси шкивов кронблока; d
0
- диаметр шкива
талевой системы; j - число несущих ветвей талевой системы. Вычислим усилие
N
0
, возникающее в ветвях талевой системы (в талевом канате) в процессе буре-
ния скважины.
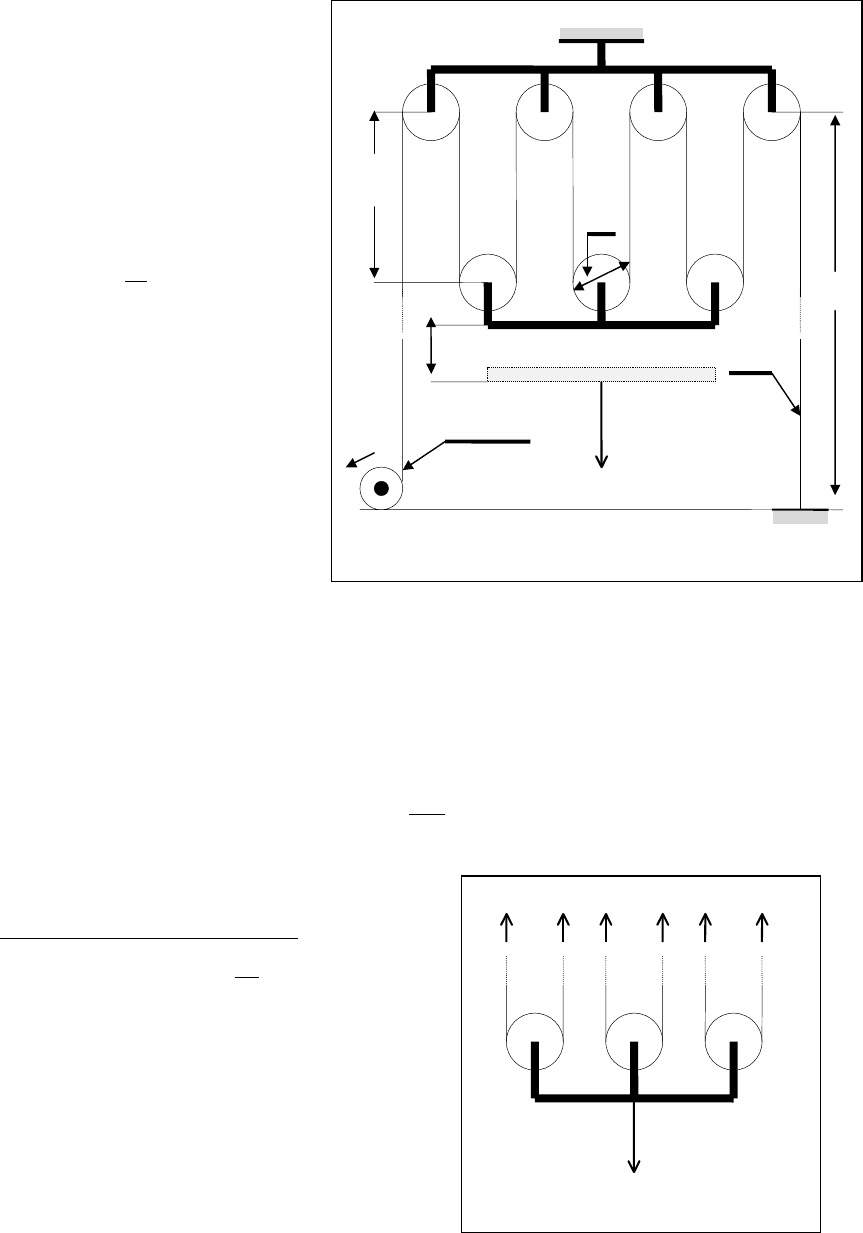
56
Очевидно, что общая длина ра-
бочей части талевого каната, смо-
танной с барабана (размерами са-
мого барабана пренебрегаем), в не-
нагруженном состоянии запишется
(это легко установить из рис.3.12):
l
0
d
0
S
0
∆
l E
T
,F
T
Барабан P
Т
).j(djiS
00
++= S 1
2
2 +
π
В нагруженном состоянии (сила
Р
Т
, создаваемая частью веса бу-
рильной колонны) длина каждой
несущей ветви увеличится на дли-
ну
∆
l из-за продольной деформа-
ции. Следовательно, суммарное
увеличение общей длины каната
.ljS
∆
∆
=
Тогда согласно закону Гука (2.1.1) легко получить, что усилие в одной ветви
талевой системы, равное усилию в канате (поскольку блок величину усилия не
меняет), можно представить, как
S
S
FEN
TT
∆
=
0
.
Отсюда с учетом значений
∆
S и S имеем:
N
jE F l
Sjl j d
TT
0
00 0
21
2
=
+++
∆
()
.
π
(3.2.2)
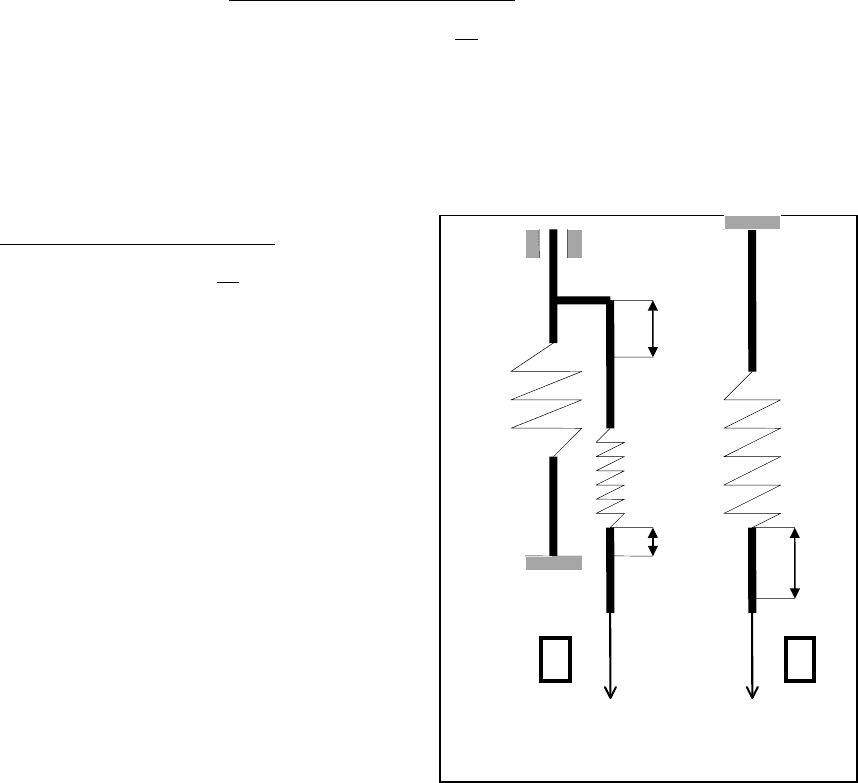
Очевидно, что суммарное усилие в ветвях
талевой системы (см. рис.3.5) должно уравно-
вешивать внешнюю нагрузку (силу от воздей-
ствия на талевую систему веса бурильной ко-
лонны). Это условие может быть записано в
виде :
,
0
jNP
T
=
Рис.3.4
j
⋅
N
0
N
0
N
0
N
0
N
0
N
0
N
0
P
T
Рис.3.5
57
откуда после подстановки N
0
согласно формуле (3.2.2) получаем:
.l
d)j(jlS
FEj
P
TT
T
∆
π
000
2
2
12 +++
=
Сравнив теперь эту запись с записью закона Гука для пружины Р
Т
= с
Т
∆
l, где
с
Т
- коэффициент упругости пружины, окончательную запись коэффициента уп-
ругости талевой системы с
Т
представим в следующем виде:
с
jEF
Sjl j d
T
TT
=
+++
2
00 0
21
2
()
.
π
(3.2.3)
Определим теперь суммарную приведен-
ную упругость талевой системы и буровой
вышки, поскольку последняя может тоже
существенно влиять на значение коэффици-
ента упругости крепления верхней части бу-
рильной колонны.
Пусть буровая вышка обладает коэффи-
циентом упругости с
в
. Тогда схематично уп-
ругую систему, включающую буровую выш-
ку и талевую систему, можно представить
так, как это изображено на рис.3.6,поз.1.
На этом же рисунке представлена эквива-
лентная пружина с эквивалентным коэффициентом упругости с (рис.3.6,поз.2).
Пусть
δ
в
- вертикальное перемещение вышки, вызванное силой Р
Т
,
δ
- деформа-
ция условной (эквивалентной) пружины с коэффициентом упругости с,
δ
Т
- де-
формация талевой системы. Тогда очевидна следующая система уравнений:
δ
в
с
в
с
с
Т
δ
Т
δ
1 2
Р
Т
Р
Т
Рис.3.6
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
=
=
+=
.сP
,сP
,сP
,
Т
ТТТ
ввТ
Тв
δ
δ
δ
δδδ
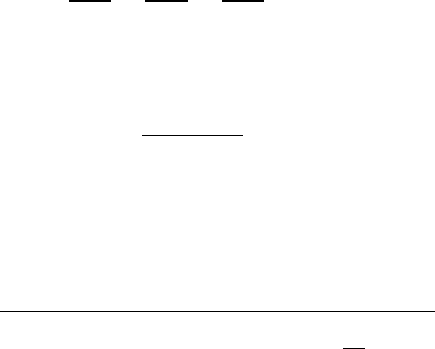
58
Выразив из трех последних равенств деформации
δ
,
δ
Т
и
δ
в
и подставив их в
первое уравнение системы, получаем:
Р
с
Р
с
Р
с
ТТ
в
Т
Т
=+.
Сократив левую и правую части на Р
Т
≠
0, найдем с :
с
сс
сс
вТ
вТ
=
+
.
После подстановки сюда значения с
Т
согласно (3.2.3) получаем окончатель-
ное выражение коэффициента упругости крепления верха бурильной колонны:
с
jEFс
jEF S jl j d c
TTв
TT в
=
++++
2
2
00 0
21
2
(()
.
π
)
t
(3.2.4)
Параметр с не остается постоянным, а изменяется в процессе углубления
скважины от предыдущего наращивания бурильной колонны к очередному. Ес-
ли через l
H0
обозначить начальное значение длины ветви, а через v
п
- скорость
подачи бурильного инструмента, то очевидно, что текущее значение l
0
будет
равно:
ll vd
Hn
t
00
0
=+
∫
,
(3.2.5)
где время t∈[0, t
K
] (t
K
- время бурения после одного наращивания колонны бу-
рильных труб).
Следовательно, коэффициент с является переменной во времени величиной.
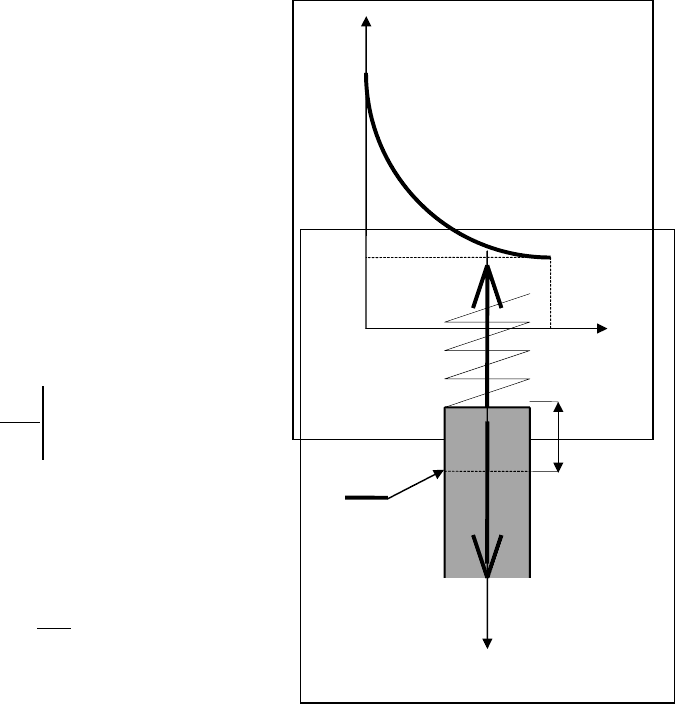
Примерный характер его изменения показан на рис.3.7. Коэффициент с изменя-
ется от максимального значения с
1
при t = 0 в момент начала бурения после на-
ращивания бурильной колонны до минимального значения с
К
при t = t
К
, когда
долото углубилось на величину ведущей трубы. Однако изменение во време-
ни этого коэффициента пренебрежимо мало по сравнению со скоростями проте-
кания волновых процессов в бурильной колонне, а потому принимаем его мед-
ленно изменяющимся параметром, что позволяет при проведении соответст-
вующих исследований считать его постоянной величиной. Указанное допуще-
59
ние позволит существенно упростить дальнейшие выкладки без привнесения
существенных погрешностей в конечные результаты.
Теперь запишем граничное условие на устье.
Для этого обратимся к рис.3.8, где схематиче-
ски изображено крепление верха бурильной ко-
лонны. При х=0 имеем, что со стороны услов-
ной пружины (буровая вышка и талевая систе-
ма)
c(t)
c
1
действует сила
N
2
= сu(0,t), где u(0,t) - переме-
щение верхнего сечения бурильной колонны;
сила N
1
, действующая в сечении, согласно зако-
ну Гука представляется, как
c
2
0 t
K
t
Рис.3.7
NEF
du
dx
x
1
=
N
2
c
0
u(0,t)
E, F
0=
.
Приравнивая силы N
1
и N
2
(по третьему зако-
ну Ньютона они равны между собой), получаем
граничное условие на устье скважины:
xEF
du
dx
cu==0: .
(3.2.6)
Выделим на расстоянии х (рис.3.3) от верхне-
го торца малый элемент стержня длиной ∆x и составим уравнение его равнове-
сия. Для этого обратимся к рис.3.9, на котором показан данный элемент массой
∆m =
ρ
F∆x, где
ρ
, F и ∆х - соответственно плотность материала, площадь попе-
речного сечения и длина элемента стержня (поскольку рассматривается одно-
родный стержень с неизменным поперечным сечением, то
ρ
и F в данном слу-
чае постоянные величины). Предположим, что на единицу длины стержня дей-
ствует сила сопротивления вертикальному перемещению стержня f
S
, вид кото-
рой на данном этапе для нас не принципиален. Кроме этого к элементу прило-
жена сила его веса ∆mg, где g - ускорение свободного падения. Проектируя
силы, действующие на элемент стержня, на ось х, запишем уравнение равнове-
сия:
N
1
x
Рис.3.8
60
,mgxf)x(N)xx(N
S
0
≈
+−−+
∆
∆
∆
где N(x) и N(x+∆x) - нормальные уси-
лия соответственно в верхнем и ниж-
нем сечениях элемента.
Воспользовавшись теперь соотно-
шением (2.1.4), поделив левую и пра-
вую части полученного равенства на
∆m =
ρ
F∆x и устремив ∆х
→
0, после
несложных преобразований получаем
искомое уравнение:
du
dx
fgF
E
F
2
ρ
.
S
2
=
−
(3.2.7)
x N(x) u(x)
∆x ∆mg
f
S
∆x
N(x+∆x)
x
Рис.3.9
Очевидно, что
ρ
gF является по-
гонным весом бурильной колонны
(весом единицы ее длины). Обозначив
этот параметр через q=
ρ
gF, оконча-
тельно имеем:
du
dx
fq
EF
S
2
2
=
−
.
(3.2.8)
Граничные условия: 1.
xEF
du
dx
cu==0: .
2. х=Н :
EF
du
dx
P=− .
В предположении постоянства по длине бурильной колонны сил сопротивле-
ния (параметр f
S
= сопst) задача (3.2.8) легко решается, а ее решение записывает-
ся как
2
2
x
EF
fq
x
c
EF
EF
тH)fq(
)x(u
. (3.2.9)
SS
−
−
⎟
⎠
⎞
⎜
⎝
⎛
+
−−
=
