Юнин Е.К. Введение в механику глубокого бурения
Подождите немного. Документ загружается.


21
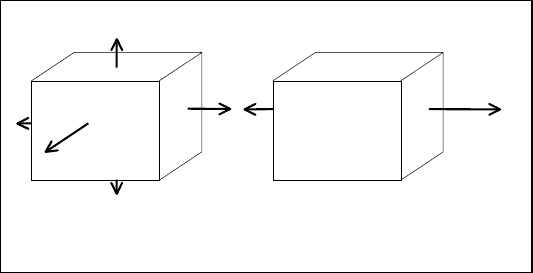
ругих деформаций (а именно этот вид деформации нами рассматривается) вы-
полняется закон Гука, то между деформацией
∆
r и усилием Р имеет место ли-
нейная зависимость, показанная в соответствующих координатных осях в пра-
вой части рис.1.13. Очевидно, потенциальная энергия стержня длиной
r и пло-
щадью поперечного сечения
F будет равна работе усилия Р, приложенного к
торцу стержня, на пути
∆
r, причем усилие будет меняться от нуля до некоторой
конечной величины. Работа же силы
Р на перемещении
∆
r равна площади тре-
угольника
0а
∆
r, откуда U
01
= 0,5Р
∆
r. Это равенство с учетом Р =
σ
F и
∆
r =
ε
r
можно переписать
,VrFrFU
2
1
2
1
2
1
01
εσεσεσ
===
где
V = Fr является объемом стержня. А теперь легко записать потенциальную
энергию деформации элемента
U
0
, как сумму работ нормальных сил на упругих
перемещениях в направлении осей
х, у и z. Так как сила, перпендикулярная пе-
ремещению, работы не производит, то, обозначив через
V
0
объем выделенного в
сплошной среде элемента (см. рис.1.12), найдем, что
.V)(VVVU
zyxzyx 03210302010
2
1
2
1
2
1
2
1
εσεσεσεσεσεσ
++=++=
Обозначив через
u
0
отношение U
0
/V
0
, то есть энергию, приходящуюся на
единицу объема, окончательно получаем:
).(u
zyx
εσεσεσ
3210
2
1
++= (1.1.16)
Положив теперь в соотношениях (1.1.11)
σ
x
=
σ
1
,
σ
y
=
σ
2
,
σ
z
=
σ
3
и подставив
полученные значения
ε
x
,
ε
y
,
ε
z
в (1.1.16), после несложных преобразований име-
ем:
[]
и
Е
01
2
2
2
3
2
12 23 31
1
2
2= ++− + +
σσσ µσσσσσσ
().
(1.1.17)
Потенциальная энергия (1.1.17) состоит из суммы двух частей, соответст-
вующих напряженным состояниям в случае шарового тензора и девиатора на-
пряжений (см. рис.1.12):
и
0
= и
об
+ и
ф,

22
где и
об
именуется энергией изменения объема, а и
ф
- энергией формоизмене-
ния
.
Энергию изменения объема найдем после подстановки в (1.1.17) значений
σ
1
=
σ
2
=
σ
3
= р, где р определяется формулой (1.1.15):
и
Е
об
=
−
++
12
6
123
2
µ
σσσ
().
(1.1.18)
Энергию же формоизменения найдем, вычитая из
и
0
величину и
об
, что после
ряда преобразований дает:
[]
и
Е
ф
=
+
−+−+−
1
6
12
2
23
2
31
2
µ
σσ σσ σσ
()()().
(1.1.19)
1.2. Элементы теории предельных напряженных состояний
В случае нагружения материальной среды посредством силовых факторов,
она может находиться в различных механических состояниях: при малых силах
нагружения, вызывающих малые напряжения, - в упругом состоянии; при воз-
растании сил, когда уже обнаруживаются остаточные деформации, - в упруго-
пластическом состоянии; наконец, по достижении некоторых значений напря
-
жений в среде происходит образование трещин и наступает состояние разруше-
ния материала.
Механическое состояние материала в точке определяется, в основном, на-
пряженным состоянием в этой точке. Однако следует сказать, что на механиче-
ское состояние могут оказывать заметное влияние такие факторы, как темпера-
тура, длительность времени силового нагружения и т.д
.
Предельное напряженное состояние - состояние материала, при котором
он переходит из одного механического состояния в другое.
Например, если
материал пластичен (на диаграмме «напряжение - деформация» имеется зона
пластичности), то предельным состоянием можно считать состояние, при кото-
ром возникают заметные остаточные деформации; для хрупкого же материала -
это состояние, при котором начинается разрушение материала. И хотя оба эти
состояния можно классифицировать как предельные, тем не менее отождеств-
лять их
нельзя, поскольку физика указанных процессов существенно различна, а
23
потому различны и условия перехода в эти состояния. Следовательно, необхо-
димо создание методов оценки меры опасности сложного напряженного состоя-
ния. Решение этой задачи является содержанием теории предельных напряжен-
ных состояний (теорий прочности).
Для оценки напряженного состояния некоторого материала его сравнивают с
некоторым напряженным состоянием, выбранным в качестве эталона. Очевид-
но,
что за такой эталон (эквивалент) удобнее всего принять одноосное на-
пряженное состояние (растяжение-сжатие) с главным напряжением
σ
экв
(рис.1.14).
Эквивалентное напряжение
σ
экв
- напряжение, которое надо
создать в растянутом (сжатом)
образце, чтобы его напряженное
состояние было равноопасно с
заданным.
Следовательно, задача состоит
в отыскании
σ
экв
через главные напряжения
σ
1
,
σ
2
,
σ
3
.
σ
3
σ
2
σ
экв
∼
σ
1
Рис.1.14
С возникновением необходимости вести расчеты на прочность был выдвинут
ряд гипотез.
В качестве критерия прочности предлагалось брать величину наибольшего
нормального напряжения
σ
1
без учета
σ
2
и
σ
3
, то есть
σ
экв
=
σ
1
. Однако практика
не подтвердила его.
Разрушение материала по плоскости можно рассматривать как результат пре-
одоления межмолекулярных сил сцепления из-за увеличения расстояния между
молекулами. На основании данного факта была предложена гипотеза, где в
качестве критерия предельного состояния принималась наибольшая линейная
деформация (в этом случае эквивалентное напряжение находят исходя из обоб
-
щенного закона Гука, записанного через главные напряжения:
)(
экв 321
σ
σ
µ
σ
σ
+−= ). Однако практика не подтвердила и этот критерий.
Известно, что образование остаточных деформаций в пластических материа-
лах происходит путем сдвига частиц относительно друг друга. Это явление вы-

24
звало к жизни гипотезу, предлагавшую брать в качестве критерия перехода от
упругого состояния к пластическому наибольшее касательное напряжение в
точке. Обратимся к напряженному состоянию, изображенному на рис.1.8. Для
этого напряженного состояния нами получены следующие значения главных
напряжений:
σ
1
=
τ
,
σ
2
= 0,
σ
3
= -
τ
. Отсюда легко найти, что
τ
σ
σ
=
−
13
2
.
Очевид-
но, что в данном случае найденное значение касательного напряжения является
максимальным:
τ
=
τ
max
. Можно показать, что это положение справедливо и для
общего случая напряженного состояния, то есть
.
max
2
31
σ
σ
τ
−
=
Очевидно, что для эквивалентного напряженного состояния (см. рис.1.14)
σ
1
=
σ
экв
,
σ
2
=
σ
3
= 0. Отсюда видно, что в этом случае
τ
max
= 0,5
σ
экв
. Приравнивая
значения максимальных касательных напряжений, получаем:
σ
σ
σ
экв
=
−
1
.
3
(1.2.1)
Полученное соотношение является
критерием Треска. Экспериментальная
проверка этого выражения при различных напряженных состояниях показала,
что переход от упругого к пластическому состоянию действительно определяет-
ся разностью между максимальным и минимальным главными напряжениями. В
числовом отношении (1.2.1) в случае пластичных материалов приводит к удов-
летворительным результатам, однако обнаруживает заметные погрешности для
материалов, имеющих различные механические характеристики при растяжении
и сжатии.
Рассмотрим теперь критерий, основанный на энергии формоизменения. В
этом случае в качестве критерия перехода из упругого состояния в пластическое
принимается соотношение (1.1.19).
Для случая одноосного напряженного состояния (рис.1.14) положив в (1.1.19)
σ
1
=
σ
экв
,
σ
2
=
σ
3
=0, имеем:
.
E
u
эквф
2
2
6
1
σ
µ
+
=

25
После приравнивания полученного значения и
ф
и значения и
ф
, даваемого
формулой (1.1.19) для общего случая, найдем, что
σσσσσσ
экв
=−+−+−
1
2
12
2
23
2
31
2
()()(
σ
).
(1.2.2)
Записанное равенство дает
критерий Мизеса. Этот критерий, несмотря на
некоторую искусственность исходных предпосылок, вполне удовлетворительно
подтверждается экспериментом.
Следует отметить, что соотношения (1.2.1) и (1.2.2) дают в числовом отноше-
нии близкие результаты, а потому все замечания, высказанные выше для (1.2.1),
верны и в отношении (1.2.2). Эти два критерия являются наиболее употреби-
тельными и не потеряли своего значения до настоящего времени
.
В заключение данного раздела заметим, что весьма простой и в то же самое
время очень плодотворной является теория прочности, предложенная О.Мором,
которая построена в предположении независимости предельного состояния от
промежуточного главного напряжения (принимается, что это состояние опреде-
ляется только максимальным и минимальным главными напряжениями). Одна-
ко этой теории здесь
мы не касаемся.
1.3. Напряженное состояние горных пород вокруг бурящейся
скважины (задача С.Г. Лехницкого)
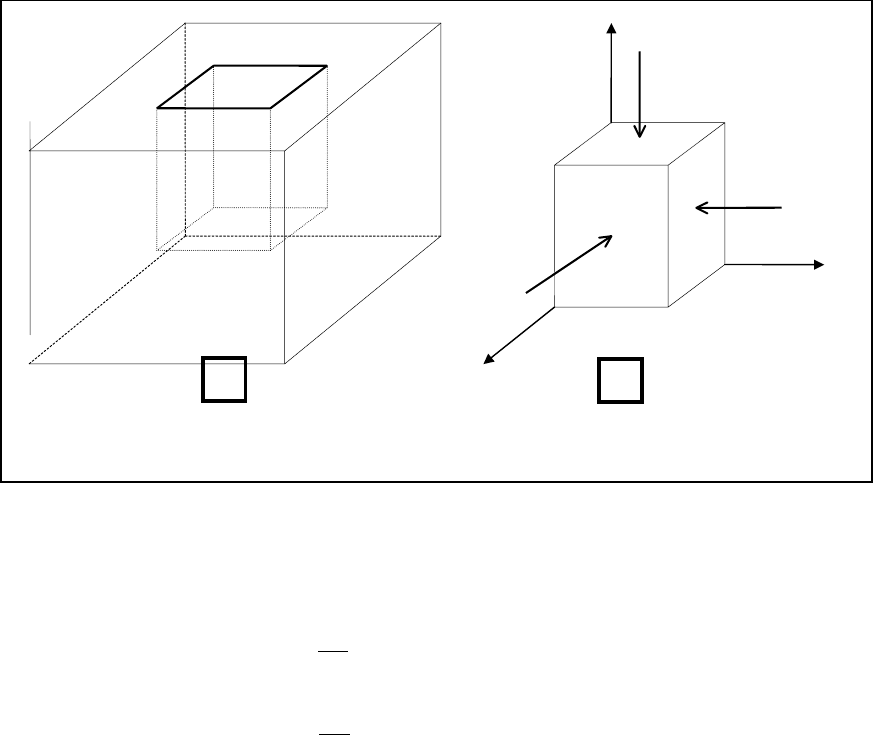
Пусть образец в виде прямоугольного параллелепипеда, изготовленного из
материала с коэффициентом Пуассона
µ
, помещен в абсолютно жесткую оправ-
ку, причем верхняя грань образца свободна, а между остальными гранями и оп-
равкой отсутствует трение (рис.1.15,поз.1). В некоторый момент в перпендику-
лярном направлении на свободную грань образца действует напряжение
σ
z
. Рас-
смотрим его напряженное состояние. Очевидно, что в силу отсутствия на кон-
тактирующих гранях параллелепипеда и оправки трения отсутствуют касатель-
ные напряжения, а потому на гранях образца действуют только нормальные на-
пряжения
σ
x
и
σ
y
(рис.1.15,поз.2).
26
z
σ
z
σ
y
y
σ
x
x
1 2
Рис.1.15
Обратимся теперь к соотношениям (1.1.11). Для рассматриваемого случая
они запишутся:
[]
[]
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+−=
+−=
.)(
E
,)(
E
xzyy
zyxx
σσµσε
σσµσε
1
1
Здесь, очевидно, нормальные напряжения
σ
x
,
σ
y
,
σ
z
являются одновременно
и главными напряжениями.
Поскольку образец заключен в абсолютно жесткую оправку, то при указан-
ном способе нагружения он не может деформироваться в поперечных направле-
ниях, то есть деформации
ε
х
=
ε
у
= 0. Следовательно, положив в записанной сис-
теме левые части нулю, получаем уравнения для определения напряжений
σ
х
и
σ
у
через
σ
z
:
σµσµσ
µσ σ µσ
xyz
xy
−=
−+=
⎧
⎨
⎩
,
.
z
Решив полученную систему, имеем:
27
σ
σ
λ
σ
xy z
=
=
,
(1.3.1)
где параметр
λ
µ
µ
=
−1
называется коэффициентом бокового распора.
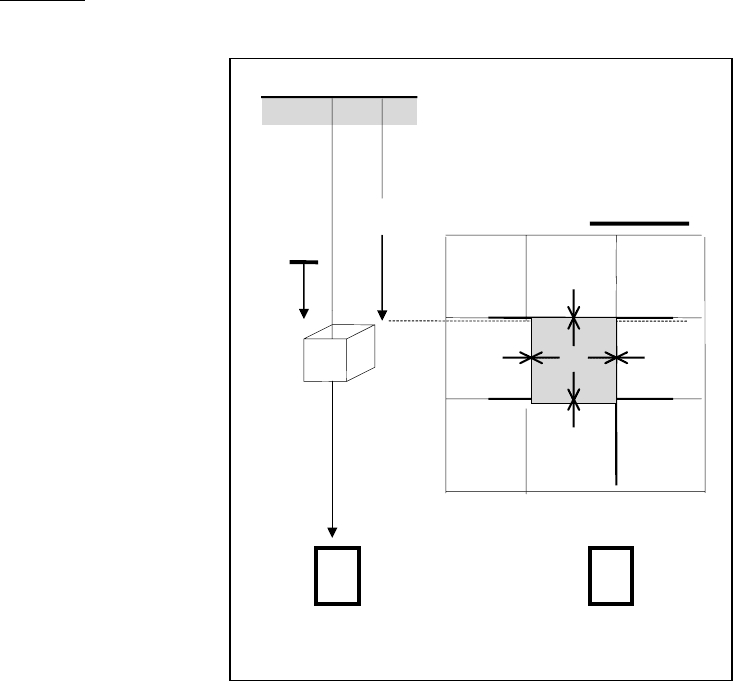
Рассмотрим теперь полупро-
странство, ограниченное поверхно-
стью Земли, и пустим из некоторой
точки
О поверхности вглубь коор-
динатную ось
Oz (рис.1.16,поз.1).
Пусть
γ
1
-средний удельный вес гор-
ных пород. Тогда, очевидно, на глу-
бине
z в плоскости, параллельной
земной поверхности, нормальное
напряжение
σ
z
= -
γ
1
z (знак «минус»
указывает на то, что напряжение -
сжимающее). Выделим мысленно на
глубине
z элементарный параллеле-
пипед, аналогичный рассмотренно-
му выше. Очевидно, что в силу отсутствия свободы деформирования в горизон-
тальном направлении, поскольку все рядом лежащие локальные элементы при
выпучивании в горизонтальном направлении в одинаковой степени взаимодей-
ствуют между собой с одинаковыми и противоположно направленными силами
(см. рис.1.16,поз.2, где искомый элемент затенен), все
элементы остаются на
месте по горизонтальным направлениям. Легко видеть, что рассматриваемый
элементарный параллелепипед находится в аналогичных условиях с вышерас-
смотренным (рис.1.15). Стягивая его в точку и воспользовавшись формулами
(1.3.1), получаем напряженное состояние в точке горной породы в условиях ес-
тественного залегания:
O
γ
1
Вид по А
z
А
z
1 2
Рис.1.16

28
⎪
⎩
⎪
⎨
⎧
−
=−=
−
=
=
.,z
,z
z
yx
µ
µ
λγσ
λγ
σ
σ
1
1
1
(1.3.2)
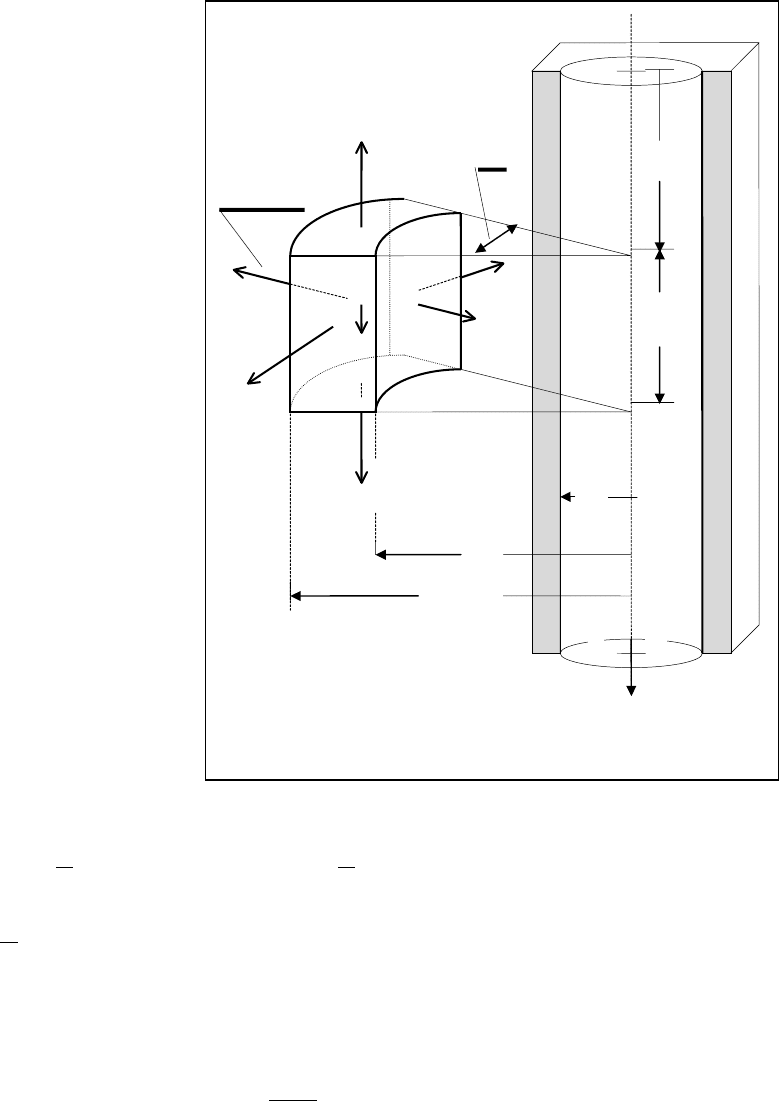
А теперь рассмотрим распределение напряжений в полупространстве, когда в
нем пробурена вертикальная глубокая скважина, заполненная жидкостью с
удельным весом
γ
2
(рис.1.17). Искомую задачу будем рассматривать в цилинд-
рической системе координат
(z,r,
θ
), где z - текущая глубина скважины, r - рас-
стояние от оси скважины до рассматриваемой точки массива горной породы,
θ
-
угол между плоскостями, проведенными через ось Оz, одна из которых фикси-
рована, а вторая проходит через рассматриваемую точку массива. Выделим
двумя коаксиальными цилиндрами с радиусами
r и r+
∆
r и плоскостями, две из
которых параллельны земной поверхности, и расстояние между ними равно
∆
z ,
а две - образуют между собой угол
∆θ
, локальный элемент на глубине z. В силу
симметрии нагрузки по границам полупространства с выемкой в виде кругового
цилиндра (скважина) относительно оси
Oz и в отсутствии нагрузок касательного
характера (на поверхности полупространства давление будем считать рав-
ным нулю, а на стенке скважины на глубине
z согласно закону Паскаля действу-
ет только давление по нормали к стенке, равное
γ
2
z), во-первых, напряжения
σ
z
в
направлении оси
Оz,
σ
r
вдоль радиуса r и
σ
θ
в направлении изменения угла
θ
не зависят от угловой координаты
θ
и, во-вторых, в выделенном элементе гор-
ной породы координатными плоскостями цилиндрической системы координат
(z,r,
θ
) отсутствуют касательные напряжения. Следовательно, искомые напряже-
ния зависят только от
z и r.
29
Очевидно, что нарушение
зависимостей (1.3.2) произой-
дет в силу изменения давления
при переходе из горной породы
в скважину из-за разностей
удельных весов
γ
1
породы и
γ
2
жидкости в скважине.
O
σ
z
(z)
∆θ
σ
r
(r+
∆
r)
γ
2
z
γ
1
σ
θ
σ
r
(r)
∆
z
σ
θ
σ
z
(z+
∆
z) r
0
r
r+
∆
r
z
Рис.1.17
Рассмотрим равновесие эле-
мента породы. Высота элемента
-
∆
z, расстояние между его
цилиндрическими поверхно-
стями -
∆
r, угол между боко-
выми плоскими гранями -
∆θ
(все эти параметры считаем
весьма малыми, в пределе
стремящимися к нулю). На
элемент действуют силы, соз-
даваемые напряжениями на его
гранях, и сила веса элемента.
Проектируя силы на ось
Оz,
имеем:
[]
[
]
[]
,r)rr()z(
zr)rr(r)rr()zz(
z
z
0
2
1
2
1
2
1
22
22
1
22
≈−+
→−−++−++
θ∆∆σ
∆θ∆∆γθ∆∆∆σ
откуда, сокращая на одинаковые множители и переходя к пределу при
∆
z
→
0,
получаем:
.
z
z
1
γ
∂
∂
σ
−= (1.3.3)
Заметим, что как сейчас, так и в дальнейшем, все производные по z и r - ча-
стные, так как напряжения
σ
z
,
σ
r
,
σ
θ
в общем случае зависят от обеих этих пе-
ременных.
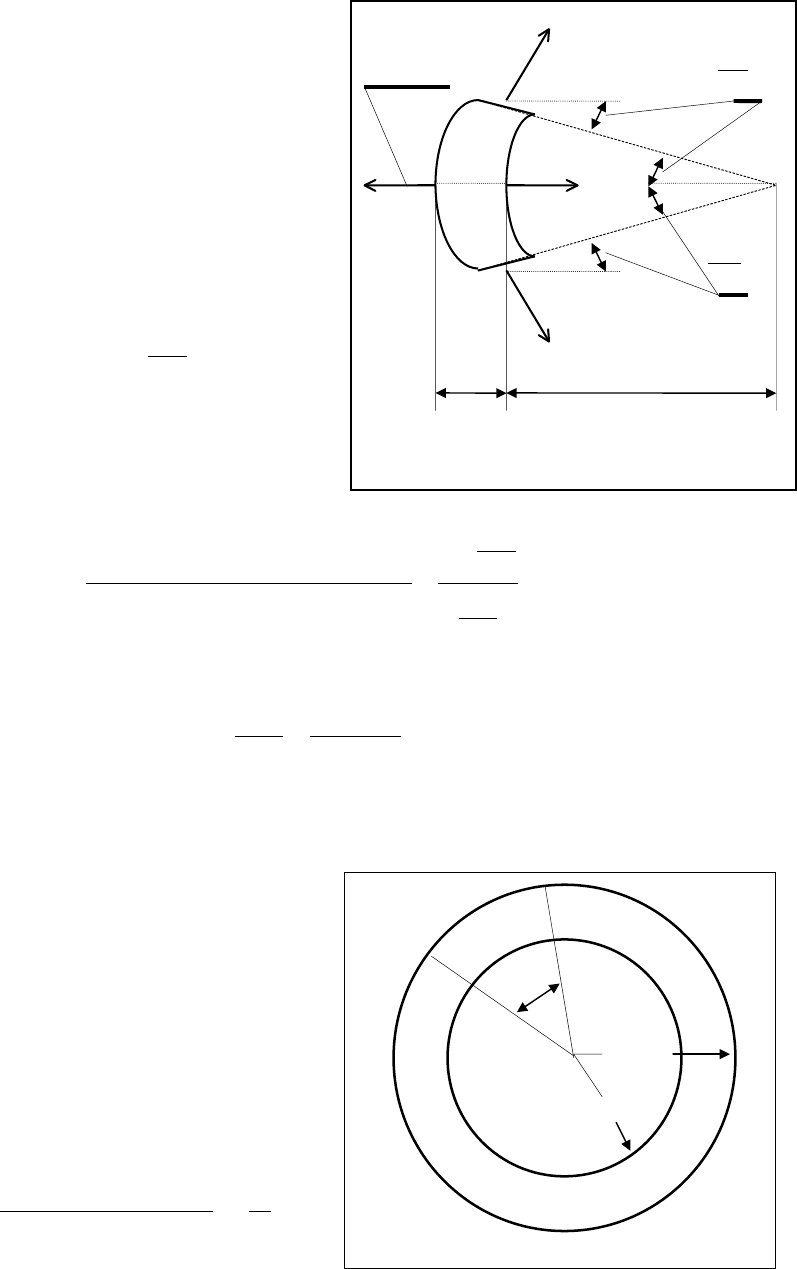
30
σ
θ
σ
r
(r+
∆
r)
2
θ
∆
σ
r
(r)
∆
θ
2
σ
θ
∆
r r
Рис.1.18
Теперь спроектируем все силы на
нормаль к цилиндрическим поверхно-
стям элемента породы, лежащую в ко-
ординатной плоскости (r,z) и делящую
угол
∆θ
пополам (рис.1.18). Очевидно,
что
.rz
z)
sinzr)r(
rr(r(
r
0
2
2 ≈−
→−++
∆∆
θ∆
σ∆θ
)r
r
∆σ
∆
∆
θ
∆
∆
σ
θ
Полученное равенство можно
переписать так:
.
sin
r
)r(r)rr()rr(
rr
0
2
2
≈−
−++
θ
σ
θ∆
θ
∆
∆
σ∆σ∆
Переходя к пределу при
∆
r
→0
и
∆θ→0
, получаем, что
.
rr
r
r
0=
−
+
θ
σ
σ
∂
∂
σ
(1.3.4)
Полученных уравнений (1.3.3) и (1.3.4) недостаточно для однозначного оп-
ределения искомых величин
σ
z
,
σ
r
и
σ
θ
. Обратимся теперь к деформациям.
Пусть при нагружении полупро-
странства радиус r цилиндрического
элемента получил приращение u(r) и
стал равен [r+u(r)] (рис.1.19). Тогда
деформация
ε
θ
в направлении угла
θ
может быть записана как отношение
разности длин «раздутой» и исходной
окружностей к длине исходной, то
есть
ε
π
π
π
θ
=
+−
=
22
2
()
.
ru r
r
u
r
С другой стороны, деформация
ε
r
в направлении радиуса может быть записана, как
∆θ
r+u(r)
r
Рис.1.19
