Юнин Е.К. Введение в механику глубокого бурения

11

lm.

z

ν

σ

ν

σ

τ

y

x

Рис.1.3

z

ν

r

О

y y

x

Рис.1.4

После подстановки сюда значений параметров

X, Y, Z согласно (1.1.3) полу-

чаем:

σσ σ σ τ τ τ

ν

=+ ++ + +

xy z yz zx xy

lmn mnnl

222

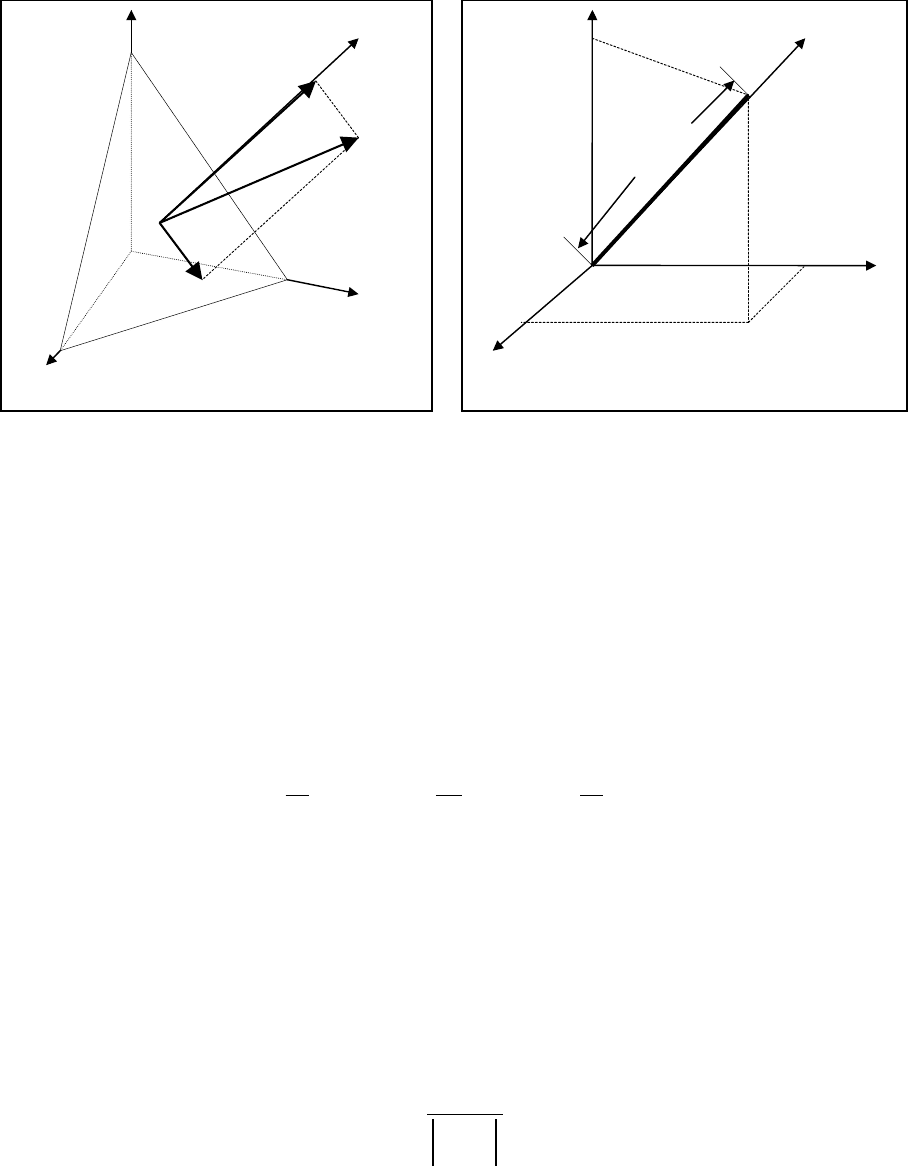
Рассмотрим теперь множество площадок общего положения, проходящих

через исследуемую точку

О (рис.1.4). По нормали к каждой площадке отложим

отрезок длиной

r (на рис.1.4 показан один из таких отрезков). Очевидно,

что косинусы направляющих углов запишутся как

,

r

z

n ,

r

y

m ,

r

x

l ===

где

х, у, z суть координаты конца отрезка длиной r.

Подставив записанные выражения для

l, m, n в выражение для

σ

ν

и совершив

несложные преобразования, имеем:

σσσσ τ τ τ

ν

r x y z xy xz yz

xyz xy xz yz

2222

222=+++ + + .

Выберем теперь параметр

r таким, чтобы выполнялось равенство

r

k

2

=

σ

ν

,

где

k - постоянная величина, отражающая масштаб построения.

Тогда после подстановки этого значения

r

2

в предыдущее выражение полу-

чим квадратичную форму, дающую центральную поверхность второго порядка:

12

0

Y ,lX

2

σσσ τ τ τ

xyz xy xz yz

xyz xyxz yzk

222

222+++ + + =m .

Выбрав соответствующие оси координат, записанную квадратичную форму

можно привести к каноническому виду, то есть к виду, когда коэффициенты при

парных произведениях координат

xy, xz. yz обращаются в нули. В рассматривае-

мом случае это говорит о том, что в исследуемой точке можно выбрать систему

координат, в которой касательные напряжения отсутствуют. Эти оси координат

называются

главными осями, а соответствующие им площадки - главными

площадками

. Нормальные же напряжения, действующие на этих площадках,

именуются

главными напряжениями. Главные напряжения в порядке их убы-

вания будем обозначать символами

σ

1

,

σ

2

,

σ

3

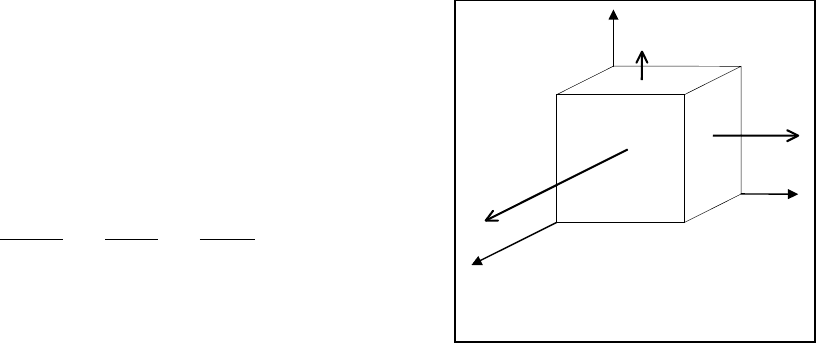
. Пример подобной ситуации по-

казан на рис.1.5. Очевидно, в данном случае система условий равновесия (1.1.3)

выделенного элемента существенно упрощается и принимает вид

.nZ ,m

31

σ

=

σ==

2

1++=,

σ

Так как верно равенство

lmn

22

то из записанных равенств легко найдем, что

.

Z

1

2

3

2

YX

2

1

2

=

σ

+

σ

+

σ

2

Записанное выражение в координатах

(X,Y,Z) является эллипсоидом с полуосями

σ

1

,

σ

2

,

σ

3

. Полученный эллипсоид называется эллипсоидом напряжений. Ве-

личины же

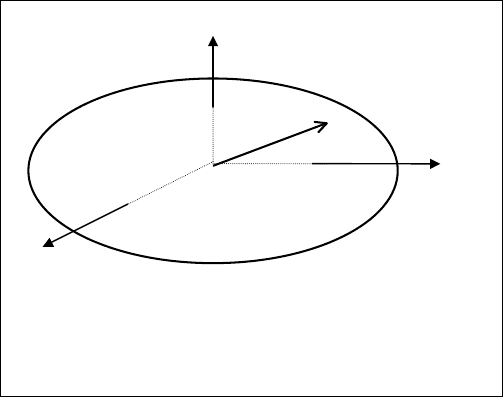
X, Y, Z можно рассматривать как координаты конца вектора полно-

го напряжения

р, действующего на площадке произвольного наклона, прохо-

дящей через выделенную в деформированном теле точку (рис.1.6). Так как

σ

1

является наибольшей осью эллипсоида, а

σ

3

- наименьшей, то очевидно (см.

рис.1.6), что наибольшее из главных напряжений является максимальным из

всего множества значений полного напряжения

р, действующего на любой

площадке произвольного наклона, проходящей через точку

О, а минимальное

главное напряжение будет наименьшим из множества значений полного напря-

жения.

z

σ

3

σ

2

σ

1

y

x

Рис.1.5

13

Очевидно, что при равенстве двух

главных напряжений эллипсоид ста-

новится эллипсоидом вращения, и

любая плоскость, проходящая через

ось вращения, является главной. Если

же равны все три главных напряже-

ния, то эллипсоид преобразуется в

сферу, и любая плоскость, проходя-

щая через исследуемую точку

О, бу-

дет главной.

Z

σ

3

p

O

σ

2

Y

σ

1

X

Рис.1.6

Займемся теперь задачей определения главных напряжений. Пусть некоторая

наклонная площадка является главной. Тогда, в силу отсутствия касательных

напряжений, нормальное напряжение

σ

, действующее на этой площадке, будет

связано со своими компонентами

X, Y, Z следующим образом:

.nZ ,mY ,lX

σ

=

σ

=

σ=

А тогда соотношения (1.1.3) примут вид

(1.1.5)

σσ τ τ

στ σ τ

στ τ σ

ll mn

mlm

nlm

xyx zx

xy y zy

х zyz z

=+ +

⎧

⎨

⎪

⎩

⎪

,

.

n

,

.

n

Перепишем (1.1.5) так:

(1.1.6)

()

σσ τ τ

τσστ

ττ σσ

xyxzx

xy y zy

xz yz z

lmn

lm

lm n

−+ + =

+− + =

++−=

⎧

⎨

⎪

⎩

⎪

0

В системе (1.1.6) неизвестными будут параметры

l, m, n.

Система линейных уравнений (1.1.6) является однородной, а потому услови-

ем не тривиальности ее решения (то есть отличие от нуля хотя бы одного из не-

известных

l, m, n) является равенство нулю определителя

14

.

zyzxz

zyyxy

zxyxx

0=

−

σσττ

τσστ

ττσσ

Раскрыв определитель, получаем уравнение относительно

σ

:

(1.1.7) ,III 0

32

2

1

3

=−+−

σσσ

где коэффициенты при степенях неизвестной величины записываются как

,I

zyx

σ

+

=

1

,I

yzxzxyzyzxyx

222

2

τττσσσσσσ

−−−++= (1.1.8)

.I

zyzxz

zyyxy

zxyxx

σττ

τστ

ττσ

=

3

Можно доказать, что корни уравнения (1.1.7) - вещественны. Они и опреде-

ляют главные напряжения

σ

1

,

σ

2

,

σ

3

.

Поскольку главные напряжения определяются только характером напряжен-

ного состояния в точке и не зависят от системы координат, то при повороте ко-

ординатных осей коэффициенты

I

1

, I

2

, I

3

остаются неизменными, а потому яв-

ляются

инвариантами тензора напряжений.

Если инвариант

I

3

=0, то один из корней уравнения (1.1.7) также равен нулю;

в этом случае напряженное состояние называется

двухосным (или же пло-

ским

). В случае I

2

=0, I

3

=0, то уравнение (1.1.7) имеет только один ненулевой

корень, а соответствующее этому случаю напряженное состояние называется

одноосным.

Рассмотрим деформацию прямоугольного образца при его растяжении

(рис.1.7). Как показывает эксперимент, удлинение образца в продольном на-

правлении (при упругой деформации) вызывает его сужение в поперечном на-

правлении. Если обозначить соответственно продольную и поперечную дефор-

мации как

,

a

,

b

nonпр

∆

=ε

∆

=ε

то опыт дает:

.

рпоп п

µε

ε

=

(1.1.9)

15

Здесь b и a соответственно

продольный и поперечный

размеры образца,

∆

b и

∆

a -

их изменения при действии

напряжения

σ

(см. рис.1.7).

Безразмерный параметр

µ

,

входящий в зависимость

(1.1.9), именуется

коэффи-

циентом Пуассона

и являет-

ся характеристикой свойств

материала образца, опреде-

ляемой экспериментально. Для всех изотропных материалов, как будет показано

ниже, величина

µ

не превосходит 0,5. Пусть связь между деформацией и напря-

жением подчиняется линейной зависимости. Тогда говорят, что материал под-

чиняется

закону Гука. При одноосном напряженном состоянии (например, рас-

тяжении или сжатии стержня) в этом случае имеем:

b

σ

a a-

∆

a

b+

∆

b

Рис.1.7

ε

σ

=

Е

.

(1.1.10)

Здесь параметр

Е именуется модулем Юнга и является характеристикой мате-

риала.

Рассмотрим элементарный параллелепипед, на гранях которого действуют

нормальные напряжения

σ

х ,

σ

у

,

σ

z

. Тогда, например, его удлинение в направле-

нии оси

х сопровождается сужением в поперечных направлениях (оси у и z),

причем это сужение определяется зависимостью (1.1.9). Одновременно подоб-

ный эффект имеет место из-за действия напряжений

σ

у

и

σ

z

, а потому, сум-

мируя компоненты деформаций вдоль соответствующих осей, имеем:

[]

εσµσσ

xxy

yyz

zzx

E

=−+

⎧

⎨

⎪

⎩

⎪

1

()

z

x

y

,

.

(1.1.11)

16

Рассмотрим теперь изменение объема элементарного параллелепипеда. По-

скольку величины его ребер равны

∆

x,

∆

y и

∆

z, то его объем V при отсутствии

деформаций запишется как

V=

∆

x

∆

y

∆

z. При действии напряжений из-за появле-

ния деформаций каждое ребро изменит свой размер и станет равным соответст-

венно

(1+

ε

x

)

∆

x, (1+

ε

y

)

∆

y и (1+

ε

z

)

∆

z. Очевидно, что изменение объема может

быть записано так:

∆

∆V xyz xyz

xyz

=+

+

−

()()()111 .

ε

Тогда после раскрытия скобок и пренебрежения, в силу малости, произведе-

ниями линейных деформаций, получим, что относительное изменение объема

eVV=∆

/

будет

e

xyz

=

+

ε

.

Подставив в полученное выражение деформации, определяемые соотноше-

ниями (1.1.11), имеем:

e

E

xyz

=

−

++

12

µ

σσσ

().

(1.1.12)

Полученное выражение объемной деформации позволяет определить наи-

большее значение коэффициента Пуассона для любого изотропного материала.

Поскольку (1.1.12) справедливо для любого напряженного состояния, то оно

применимо и для случая равенства напряжений

σ

x

=

σ

y

=

σ

z

=

σ

. В этом случае

получим, что

е

Е

=

−

3

12

µ

σ

.

Теперь будем рассуждать следующим образом. Поскольку при положи-

тельном

σ

(растяжение) объем увеличивается, а при отрицательном

σ

(сжатие) -

уменьшается, то соответственно в первом случае параметр е должен быть поло-

жительным, а во втором - отрицательным. Это возможно только в случае поло-

жительности коэффициента перед

σ

, то есть когда (1-2

µ

)

>0

, откуда и следует

искомая оценка для коэффициента Пуассона:

µ<0,5

.

17

στσ

32

−=

А сейчас рассмотрим напряженное со-

стояние, изображенное на рис.1.8. Очевид-

но, в этом случае

σ

x

=

σ

y

=

σ

z

=

τ

xz

=

τ

yz

=0,

τ

xy

=

τ

yx

=

τ

, и уравнение (1.1.7) для определе-

ния главных напряжений запишется как

0,

откуда легко найдутся главные напряжения:

σ

1

=

τ,

σ

2

= 0,

σ

3

= -

τ

.

Далее, присовокупив к системе (1.1.5)

условие равенства суммы квадратов косинусов направляющих углов единице,

получаем:

z

τ

y

x

Рис.1.8

⎪

⎩

⎪

⎨

⎧

=++

.nml

,nnml

,mnml

,lnml

zyz›z

zyyxy

zxyxx

1

222

σσττ

στστ

σττσ

Подставим сюда значения нормальных и касательных напряжений:

⎪

⎩

⎪

⎨

⎧

=++

=

.1

,0

,

222

nml

n

ml

lm

σ

στ

Из этой системы получаем, что

nlm===±0

1

2

,. Напряженное состояние бу-

дет плоским (это очевидно и из рис.1.8), а главные оси будут повернуты относи-

тельно исходного положения на угол

± 45

°

(значение знака в данном случае ро-

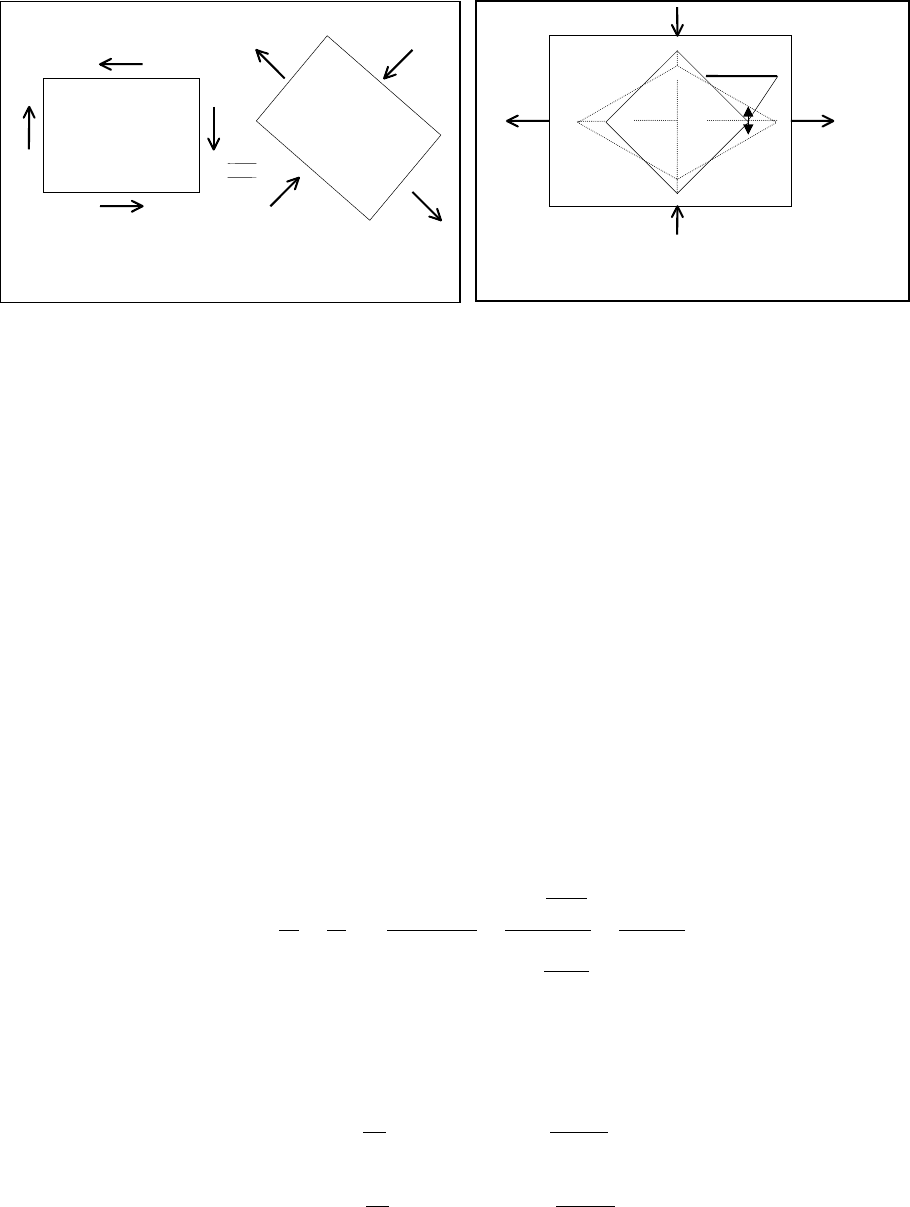
ли не играет). Если смотреть на выделенный элемент со стороны оси

z, то ис-

ходное напряженное состояние и равнозначное ему напряженное состояние в

главных осях схематично иллюстрируются так, как показано на рис.1.9.

18

τ

с 0,5

π

-

γ

с

/

τ

а

/

а О

τ

Рис.1.10

τ

Рис.1.9

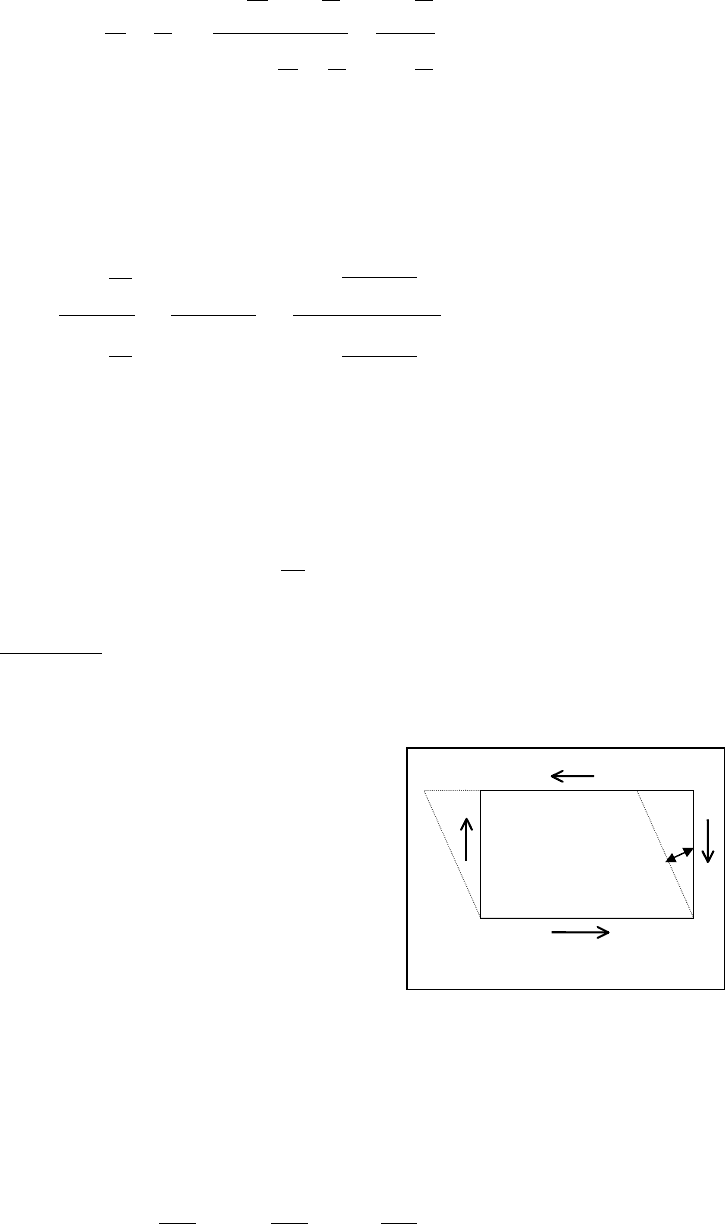
Рассмотрим теперь состояние элемента в главных осях. Оно изображено на

рис.1.10, причем для удобства параллелограмм повернут относительно своего

истинного положения на 45

°

. Пусть изначально элемент находится в ненапря-

женном состоянии. Выделим, как это показано на рис.1.10, в нем квадрат с цен-

тром в точке

О и пусть половина диагонали квадрата равна L. В результате воз-

действия силовых факторов квадрат при деформации изменяет свою форму.

При этом, в силу малости выделенного элемента, считаем, что стороны квадрата

в результате деформации претерпевают поворот и изменение размера, но сохра-

няют прямолинейную форму. Следовательно, квадрат приобретает форму ром-

ба, который на рис.1.10 показан штриховыми линиями. Рассмотрим диагонали

квадрата

аО и сО. В результате деформации они преобразуются в диагонали а

/

О

и с

/

О, а прямой угол при вершине а уменьшается на некоторую величину

γ

.

Очевидно, что угол

Оа

/

с

/

=0,5(0,5

π

-

γ

), а его тангенс вычисляется как

,

L

aa

L

cc

aaL

ccL

tg

/

2

1

24

ε

γπ

+

=

+

−

=

+

−

=

⎟

⎠

⎞

⎜

⎝

⎛

−

где через

ε

1

и

ε

2

обозначены относительные деформации (с учетом их знаков)

диагоналей

сО и аО. В силу соотношений (1.1.11) имеем, что

⎪

⎩

⎪

⎨

⎧

+

=−−=

+

−=−−=

.

E

))((

E

,

E

)(

E

τ

µ

τµτε

τ

µ

µττε

11

2

1

С другой стороны

19

.

tgtg

tg

2

1

2

1

24

1

24

γ

γπ

γ

π

γπ

+

−

≈

+

−

=

⎟

⎠

⎞

⎜

⎝

⎛

−

В последнем выражении из-за малости аргумента его тангенс заменен самим ар-

гументом.

Из полученных соотношений имеем:

.

Ѓ

τ

µ

τ

µ

ε

γ

+

−

=

+

=

+

−

1

2

1

2

1

2

1

Полученное равенство позволяет легко найти связь между угловой деформа-

цией

γ

и касательным напряжением

τ

. Опуская несложные промежуточные вы-

кладки, получаем:

,

G

τ

γ

= (1.1.13)

где параметр

)1(2

µ

+

=

E

G

называется модулем сдвига.

Смысл соотношения (1.1.13) раскрыт на рис.1.11.

Пусть напряженное состояние таково, что на

гранях выделенного элемента возникают только

касательные напряжения

τ

. Такое напряженное со-

стояние называется

чистым сдвигом. В этом слу-

чае (если условно принять нижнюю грань непод-

вижной) угловая деформация

γ

определяется со-

отношением (1.1.13). Важно отметить, что (1.1.13)

является следствием зависимостей (1.1.9) и (1.1.11). Если касательные напряже-

ния действуют по всем граням (см. рис.1.1), то искажение угла между двумя пе-

ресекающимися гранями зависит только от соответствующих компонент каса-

тельного напряжения и подчиняется зависимости (1.1.13). Отсюда получаем

τ

γ

τ

Рис.1.11

.

G

,

G

,

G

zx

yz

xy

τ

γ

τ

γ

τ

γ

=== (1.1.14)

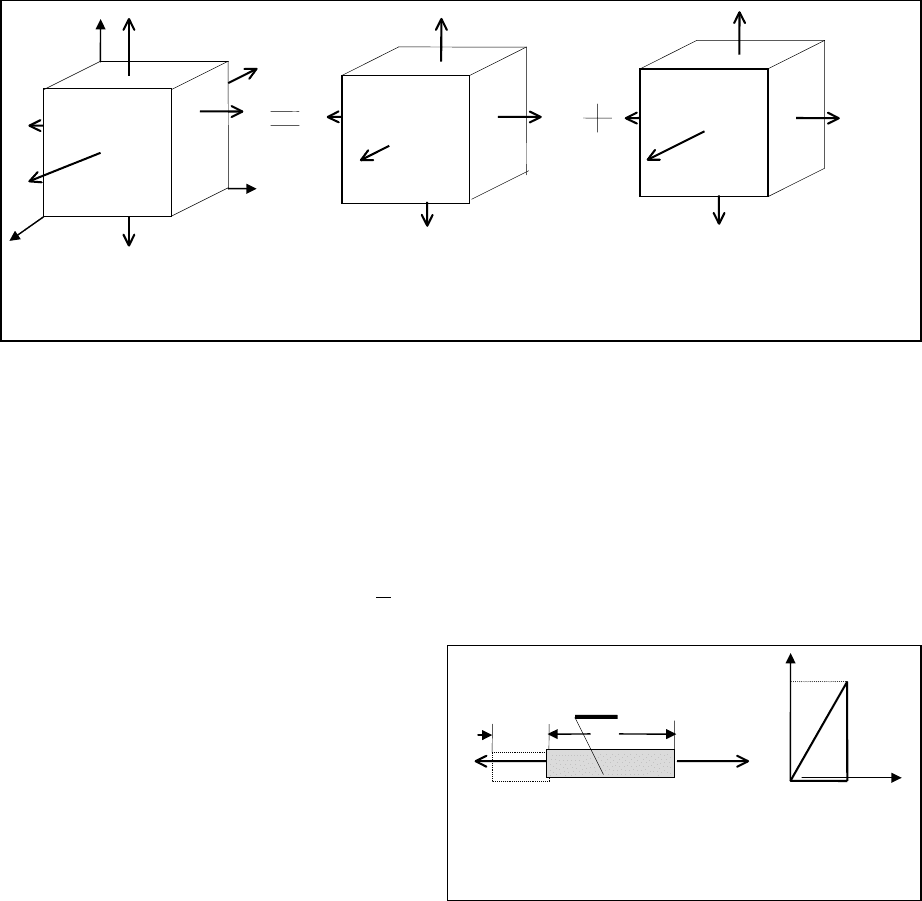
20

Соотношения (1.1.11), (1.1.12) и (1.1.14) выражают обобщенный закон Гука

для изотропного тела

. Эти соотношения подтверждаются многочисленными

экспериментами.

В заключение получим выражение для так называемой энергии изменения

формы, которое потребуется нам в дальнейшем. Для простоты напряженное со-

стояние выделенного элемента будем рассматривать в главных осях.

Обратимся к рис.1.12, где тензор напряжений представлен как сумма двух

тензоров - тензора с одинаковыми главными напряжениями

р (этот тензор назы-

вается

шаровым или же гидростатическим)

и дополнительным тензором (он именуется

девиатором напряжений):

.р,р,р

***

332211

σσσσσσ

+=+=+=

При этом требуется выполнение условия

.

***

0

321

=++

σσσ

Из записанных соотношений легко найдем, что

).(р

321

3

1

σσσ

++= (1.1.15)

Найдем потенциальную энергию

деформации

U

0

, которую запасает

элемент в результате его деформации.

Вначале рассмотрим растяжение (ли-

бо сжатие, что не принципиально)

упругого стержня длиной

r и площа-

дью поперечного сечения

F (рис.1.13)

и найдем энергию деформации

U

01

для этого случая. Поскольку в пределах уп-

z

σ

3

р

σ

3

*

σ

2

р

σ

2

*

σ

1

y р

σ

1

*

x

Рис.1.12

P

E,F P а

∆

r r

Р

0

∆

r

∆

r

Рис.1.13

Юнин Е.К. Введение в механику глубокого бурения

Подождите немного. Документ загружается.