Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

6.5. SEAMLESS COUPLING 277

how useful it will be.

6.5 Seamless coupling

With the exception of CPMD, the approaches discussed above all require converting

back and forth between the macro- and micro-states of the system. This can become

rather diﬃcult in actual implementations, particularly when constructing discrete micro-

states (needed for example in molecular dynamics) from continuous macroscale variables.

The seamless strategy proposed in [29] is intended to bypass this diﬃcult step.

To motivate the seamless algorithm, let us consider the trivial example of a stiﬀ ODE:











= f(x, y)

= −

(y − ϕ(x)).

(6.5.1)

Using the notations of earlier sections, we have U = x, u = (x, y). If we want an eﬃcient

algorithm for capturing the behavior of x without resolving the detailed behavior of y,

we can simply change the small parameter ε to a b igger value ε

′

, the size of which is

determined by the accuracy requirement (the issue of how the value of ε

′

aﬀects the

accuracy will be discussed later):











= f(x, y)

= −

′

(y − ϕ(x)).

(6.5.2)

This is then solved using standard ODE solvers. We will refer to this as “boosting”.

We can look at this diﬀerently. Instead of changing the value of ε, we may change the

clock for the microscale model, i.e. if we use τ = tε/ε

′

in the second equation in (6.5.2),

then (6.5.2) can be written as:











= f(x, y)

dτ

= −

(y − ϕ(x)).

(6.5.3)

If we discretize this equation using standard ODE solvers but with diﬀerent time step

278 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

sizes for the ﬁrst and second equations in (6.5.3), we obtain the following algorithm:

n+1

= y

−

δτ

− ϕ(x

)) (6.5.4)

n+1

= y

n+1

(6.5.5)

n+1

= x

∆tf(x

, D

n+1

). (6.5.6)

Here y

∼ y(nδτ) and x

∼ x(n

∆t). The value of δτ is the time step size we would use if

we attempt to solve (6.5.1) accurately. If (6.5.1) were the molecular dynamics equations,

then δτ would be the standard femtosecond time step size.

∆t is the time step one would

use for (6.5.2). It satiﬁes

∆t

′

δτ

(6.5.7)

In general,

∆t should be chosen such that one not only resolves the macro time scale, but

also allows the micro state to suﬃciently relax, i.e. to adjust to the changing macroscale

environment. For example, if ∆t is the time step size required for accurately resolving

the macroscale dynamics and if τ

is the relaxation time of the microscopic model, then

we should choose

∆t = ∆t/M where M ≫ τ

/δτ.

The advantage of this second viewpoint is that it is quite general, and it does not

require tuning parameters in the microscopic model. In a nutshell, the basic idea is as

follows.

1. Run the (constrained) micro solver using its own time step δτ .

2. Run the macro solver at a pace that is slower than a standard macro model:

∆t =

∆t/M.

3. Exchange data between the micro- and macro-solvers at every step.

Intuitively, what one does is to force the microscale model to accommo date the changes

in the macroscale environment (here the change in x) at a much faster pace. For example,

assume that the characteristic macro time scale is 1 second and the micro time scale is

1 femtosecond (= 10

−15

second). In a brute force calculation, the micro mo del will run

steps before the macroscale environment changes appreciably. HMM makes use of

the separation of the time scales by running the micro model only until it is suﬃciently

relaxed, which requires much fewer (say M) than 10

steps, and then extracting the

6.5. SEAMLESS COUPLING 279

data needed in order to evolve the macro system over a macro time step of 1 second.

Thus, in eﬀect, HMM skips 10

−M micro steps of calculation for the microscale model.

It exchanges data between the macro and micro solvers after every 10

micro time step

interval. The price one has to pay is that one has to reinitialize the microscale solver

at each macro time step, due to the temporal gap created by skipping 10

− M micro

steps. O ne can take a diﬀerent viewpoint. If we deﬁne

˜y(k

∆t + t

) = y

n,k

, k = 1, ··· , M (6.5.8)

where

∆t = ∆t/M and y

n,k

is th e k-th step solution to the microscale model at the

n-th macro step in HMM, the variable ˜y is deﬁned uniformly in the new rescaled time

axis. By doing so, we change the clock for the micro model (by a factor of

∆t/δt), but

we no longer need to reinitialize the micro model every macro time step , since the gap

mentioned above no longer exists. Because the cost of the macro solver is typically very

small compared with the cost of the micro solver, we may as well run the macro solver

using a smaller time step (i.e. 1/M second) and exchange data every time step. In this

way the data exchanged ten d to be more smooth. It turns out that this has the ad ded

advantage that it also reduces the statistical err or (see the numerical results presented

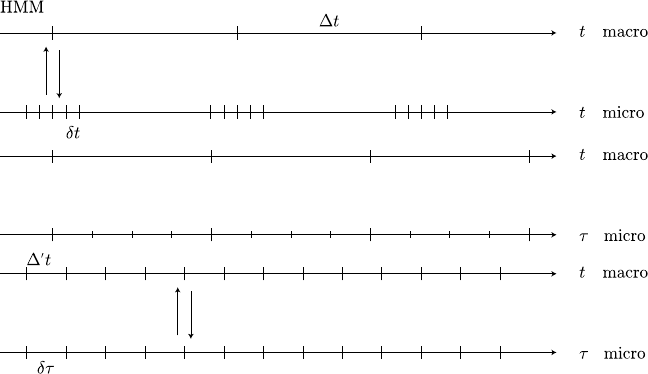
in the next section). This is illustrated in Figure 6.6.

Figure 6.6: Illustration of HMM (upper panel) and the seamless algorithm (lower panel).

Middle panel: rescaling the micro time scale.

280 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

Now we turn to the general form of the seamless algorithm proposed in [29] (see also

earlier related work in [35, 62]). Using the setu p in Section 6.3, we can write the seamless

algorithm as follows:

1. Given the current state of the micro variables u(τ) and the macro variables U(t),

evolve the micro variables for one time step

u(τ + δτ) = S

δτ

(u(τ); U(t)); (6.5.9)

2. Estimate D:

D = D(u(τ + δτ )); (6.5.10)

3. Evolve the macro variables

U(t +

∆t) = S

∆t

(U(t); D). (6.5.11)

In this algorithm, we alternate between the macro- and micro-solvers, each running with

its own time step (therefore the micro- and macro-solvers use diﬀerent clocks). At every

step, the needed macroscale d ata is estimated from the results of the micro-model (at that

step) and is supplied to the macro-solver. The new values of the macro-state variables

are then used to constrain the micro-solver.

Remarks:

1. The seamless algorithm incurs an additional cost due to the fact that we now

evolve the macro variables using much smaller time steps. However, in most cases, this

additional cost is insigniﬁcant since the cost of the micro-solver is still much bigger than

the cost of the macro-solver.

2. In HMM, we normally use time averaging to process the needed data. We may

still do that in the new algorithm. However, it is not clear that this indeed improves the

accuracy. We will r eturn to this issue later.

From the consideration of time scales alone, the computational savings in the seamless

algorithm come from the fact that eﬀectively the system evolves on the time step

∆t. In

the case when the time-scales are disparate,

∆t can be much larger than δτ . Therefore

one can deﬁne the savings factor:

∆t

δτ

∆t

Mδτ

(6.5.12)

6.5. SEAMLESS COUPLING 281

As an example, let us consider the case when the microscopic model is molecular dynam-

ics, and the time step size is femtoseconds (δτ = 10

−15

seconds). If one wants to simulate

one second of p hysical time, then one needs to compute for 10

steps. On the other

hand, assume that the relaxation time is on the order of picoseconds (10

−12

seconds)

which is about 10

micro time steps, then M = 10

is a reasonable choice. Simulating

one second of physical time using the seamless algorithm requires 10

steps. This is a

factor of 10

savings. The price to pay is that we no longer obtain accurate information

at the level of the microscopic details – we can only hope to get accurate information for

the macro-state variables.

Example 1: SDEs with multiple time scales

Consider the stochastic ODE:











= f(x, y)

= −

(y − ϕ(x)) +

˙w

(6.5.13)

where ˙w(t) is the standard white noise. The averaging theorems suggest that the eﬀective

macroscale equation should be of the form of an ODE:

= F (x). (6.5.14)

HMM with forward Euler as the macro-solver proceeds as follows:

1. Initialize the micro-solver, e.g. y

n,0

= y

n−1,M

;

2. Apply the micro-solver for M micro steps:

n,m+1

= y

n,m

−

δt

n,m

− ϕ(x

)) +

δt

n,m

(6.5.15)

m = 0, 1, ··· , M − 1. Here the {ξ

n,m

}’s are indep en dent normal random variables

with mean 0 and variance 1;

3. Estimate F (x):

m=1

f(x

, y

n,m

); (6.5.16)

282 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

4. Apply the macro-solver:

n+1

= x

+ ∆t F

. (6.5.17)

In contrast, the seamless algorithm with forward Euler scheme is simply:

n+1

= y

−

δτ

− φ(x

)) +

δτ

(6.5.18)

n+1

= x

∆t f(x

, y

n+1

) (6.5.19)

where the {ξ

}’s are independent normal random variables with mean 0 and variance

1. Note that for HMM, we have x

∼ x(n∆t), but for the seamless algorithm, we have

∼ x(n

∆t) = x(n∆t/M).

Example 2: The parabolic homogenization problem

Consider

∂

= ∂

· (a(x,

, t)∂

) (6.5.20)

where a(x, y, t) is a smooth function and is periodic in y, say with period 1. The

macroscale model is of the form

∂

U = ∂

· D (6.5.21)

D = ha(x,

, t)∂

i (6.5.22)

where h·i means taking spatial averages.

As in HMM, if we choose a ﬁnite volume method as the macro-solver, then D needs

to be evaluated at the cell boundaries [1]. We will make the assumption that the ﬂux

D depends on the local values of U and ∂

U only. Consequently for the micro model,

we will impose the boundary condition that u

(x, t) − Ax is periodic where A = ∂

U is

evaluated at the location of interest.

Denote the micro-solver as:

n+1

= S

δτ,δx

; A) (6.5.23)

In HMM, assuming that we have the numerical approximation {U

} (where t

= n∆t, U

∼

U(n∆t, j∆x)) at the n-th macro time step, we obtain the numerical approximation at

the next macro time step by:

1. For each j, let A

= (U

− U

j−1

)/∆x.

6.5. SEAMLESS COUPLING 283

2. Reinitialize the micro-solver, such that u

(x) − A

x is periodic for each j.

3. Apply the micro-solver M steps:

n,m+1

= S

δτ,δx

n,m

; A

)

with m = 0, 1, ··· , M − 1.

4. Compute

n+1

j−1/2

= ha(x,

, t

)∂

n,M

i (6.5.24)

5. Evolve the macro-state variables using

n+1

= U

+ ∆t

n+1

j+1/2

− D

n+1

j−1/2

∆x

(6.5.25)

In comparison, given {U

}, where U

denotes the numerical approximation at time

= n

∆t inside the j-th cell, the seamless strategy works as follows:

1. For each j, let A

= (U

− U

j−1

)/∆x.

2. Evolve the micro-state variable for one micro-time step:

n+1

= S

δτ,δx

; A

) (6.5.26)

3. Compute

n+1

j−1/2

= ha(x,

, t

)∂

n+1

i (6.5.27)

averaged over one period for the fast variable.

4. Advance the macro-state for one reduced macro-time-step:

n+1

= U

∆t

n+1

j+1/2

− D

n+1

j−1/2

∆x

(6.5.28)

It should be noted that as in HMM, the seamless algorithm is also a top-down strategy

based on a preselected macro-scale solver. In this sense, it can be regarded as a seamless

version of HMM.

284 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

6.6 Application to ﬂuids

The examples discussed above are all rather simplistic. As a more realistic example,

we discuss how HMM and the seamless algorithm can be used to model the macroscopic

ﬂuid dynamics of complex molecules, under the assumption that the stress depends only

on the rate of strain.

The basic formulation. The microscopic model we will use is a molecular dynamics

model for chain molecules. Assume that we have N molecules, each molecule consists of

L beads connected by springs. Each bead moves according to Newton’s equation:

dτ

= −

∂V

∂x

(6.6.1)

where j = 1, . . . , LN accounts for all the beads. The interaction potential consists of two

parts:

1. All beads interact via the Lennard-Jones (LJ) potential:

(r) = 4ε







−







(6.6.2)

where r is the distance between the beads, ε

and σ are some energy and length

parameters, respectively.

2. There is an additional interaction between neighboring beads in each molecule via

a spring force, modeled by the FENE potential (see Section 5.1):

FENE

(r) =











1 −





if r < r

∞ if r ≥ r

(6.6.3)

In principle, we should work with a set of compressible ﬂow equations at the macro

level, and an NVE ensemble at the micro level, as was discussed earlier in Section 6.3,

using (6.3.15) as the starting point for linking between the macro and micro models.

In practice, we will make two approximations for the sake of convenience: First, we will

assume that the ﬂow is incompressible at the macroscale. Secondly, we will work with the

NVT ensemble in molecular dynamics, i.e. we will impose constant temperature in the

6.6. APPLICATION TO FLUIDS 285

MD [36] (see Section 4.2). The constant temperature constraint is imposed by using vari-

ous kinds of thermostats [36]. After making these two assumptions, the conservation laws

(6.3.15) with σ deﬁned by the Irving-Kirkwood formula are no longer exact. However, we

will continue to use the Irving-Kirkwood formula as the basis for extracting macroscopic

stress from the MD data. This should be an acceptable approximation but its accuracy

remains to be carefully validated. For simplicity only, we will also limit ourselves to the

situation when the macroscale ﬂow is a two dimensional ﬂow. The molecular dynamics,

however, is done in three dimensions, and simple periodic boundary condition is used in

the third direction.

The macroscale model and the macro-solver. We will assume that the macro-

scopic density is a constant ρ

. Under this assumption, the macroscopic model should

be of the form:







(∂

U + ∇ · (U ⊗ U)) − ∇ · σ

= 0, x ∈ Ω

∇ · U = 0

(6.6.4)

where U is the macroscopic velocity ﬁeld, σ

is the stress tensor. The data that needs to

be supplied from the micro model is the stress: D = σ

. We will make the assumption

that it depends only on ∇U. As we remarked earlier (Section 6.3), since the macroscale

model is in the form of the equations for incompressible ﬂows, it is natural to use the

projection method as the macro solver [11]. Let us denote the time step by ∆t (or

∆t

in the seamless metho d ), and the numerical solution at time t

= n∆t by U

. In the

projection method, we discretize the time derivative in the momentum equation using

the forward Euler scheme:

n+1

− U

∆t

+ ∇ · (ρ

⊗ U

− σ

) = 0. (6.6.5)

For the moment, pressure as well as the incompressibility condition are neglected. Next,

the velocity ﬁeld U

n+1

at the new time step t

n+1

= (n + 1)∆t is obtained by projecting

n+1

onto the divergence-free subspace:

n+1

−

n+1

∆t

+ ∇P

n+1

= 0, (6.6.6)

where P

n+1

is determined by the incompressibility condition:

∇ · U

n+1

= 0 (6.6.7)

286 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

In terms of the pressure ﬁeld, this becomes:

∆P

n+1

∆t

∇ ·

n+1

(6.6.8)

with a Neumann type of boundary condition.

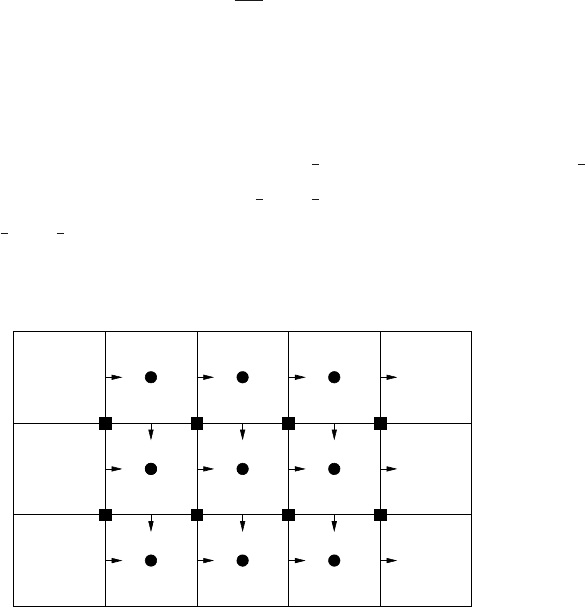
The spatial derivatives in the equations above are discretized using a staggered grid

as shown in Fig. 6.7. We denote the two components of the velocity ﬁeld by U and

V . In the staggered grid, U is deﬁned at {(x

, y

)}, V is deﬁned at {(x

, y

)}, and

P is deﬁned at the center of each cell {(x

, y

)}. The diagonal components of σ

are deﬁned at {(x

, y

)}, and the oﬀ-diagonal terms are deﬁned at {(x

, y

)}. The

operators ∇ and ∆ in the equations (6.6.5), (6.6.6) and (6.6.8) are discretized by standard

central diﬀerence and the ﬁve-point formulas respectively.

Figure 6.7: A staggered grid for the d iscretization of the spatial derivatives in the macro

model of incompressible ﬂuid dynamics. U = (U, V ). U is deﬁned at the mid-point of

the vertical edges, V is deﬁned at the mid-point of the horizontal edges, P is deﬁned at

the centers of the cell. The diagonal comp onents of the momentum ﬂux are computed at

the cell centers indicated by the circles, and the oﬀ-diagonal components are computed

at the grid points indicated by the squares.

The HMM algorithm. Given an initial value U

for the macro model, we set n = 0

and proceed as follows.

1. Compute the velocity gradient A

= ∇U

at each grid point where the stress is

needed.

2. Initialize an MD at each grid point.