Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

6.6. APPLICATION TO FLUIDS 287

3. Evolve each of the MD systems for M steps with a micro time step δτ. Each MD

is constrained by the local velocity gradient A

through the b oundary condition.

More details about this constrained MD will be discussed later.

4. Compute the stress σ

from the MD results. This is done using the Irving-Kirkwood

formula after suﬃcient number of relaxation steps. The stress is averaged over each

MD box as in (6.6.14) (see below) and also over time to reduce statistical error.

More details will be given later.

5. Evolve the macro model for one macro step to obtain U

n+1

∼ U((n + 1)∆t). This

is done using the projection method (6.6.5), (6.6.6), (6.6.8) with a macro time step

∆t and the stress computed from MD.

6. Set n := n + 1, and go to step 1.

The seamless algorithm. The seamless algorithm, on the other hand, works as

follows. At each step, we

1. Compute the velocity gradient A

= ∇U

at each grid point.

2. Evolve each MD system and the equation for the MD box (6.6.10) for one micro

time step δτ. For the MD, one uses a periodic boundary condition with respect to

an evolving box. The details of that are discussed next.

3. Compute t he stress σ

from the MD results. Similar to HMM, the stress is averaged

over the MD box.

4. Update the macro solution for one macro step

∆t to obtain U

n+1

∼ U((n + 1)

∆t).

This is done using the scheme in (6.6.5), (6.6.6), and (6.6.8) but with ∆t replaced

by the (smaller) time step

∆t.

5. Set n := n + 1, and go to step 1.

Compared with HMM, the main diﬀerence is that the micro solver (here the MD) runs

continuously without reinitialization at each time step. MD communicates with the

macro solver at every time step - the constraint (i.e. the velocity gradient) imposed on

the MD changes at each MD step while the instantaneous stress computed from MD step

288 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

is used to evolve the macro velocity ﬁeld. The simplest version of this algorithm for shear

ﬂows was introduced in [62].

Constrained MD and stress estimation. Next we discuss how to set up the

molecular dynamics in such a way to ensure that its average velocity ﬁeld coincides with

the local macroscale velocity ﬁeld. We have assumed that the stress is only a function

of the rate of strain. Therefore, associated with each macro grid point where stress is

needed, we make the approximation that the macroscale velocity ﬁeld is a linear function:

U = U

+ Ax (6.6.9)

where A is the rate of strain tensor at the given macroscale grid point. According to

our assumption, σ

depends only on A. Therefore, without loss of generality, we can

set U

= 0. We will set up a molecular dynamics system which is constrained in such

a way that its average strain rate coincides with A. This constraint is imposed by

using a periodic boundary condition for particle positions with respect to an evolving

computational box. The vertices of the MD box move according to the dynamics:

dτ

= AX(τ) (6.6.10)

When a particle goes outside the simulation box, it is inserted back from the opposite

side of the box and at the same time, its velocity is modiﬁed according to the imposed

velocity gradient:

= v

+ A(

− x

). This is a generalization of the Lees- Edwards

boundary condition for shear ﬂows [2]. See [63] for more details.

From the results of the molecular dynamics, we then compute the local stress using

a modiﬁcation of the Irving-Kirkwood formula. We split the particle velocity into two

parts:

= v

′

+ U(x

, τ) (6.6.11)

where v

′

is the ﬂuctuating part of the velocity and U(x) = h

δ(x −x

)i is the mean

velocity. Since the MD is constrained in such a way that the average velocity ﬁeld is

U = Ax, the ﬂuctuating part of t he velocity of the particles in (6.6.13) is simply given

by v

′

= v

− Ax

. The average momentum ﬂux ˜σ can then be written as:

h˜σi = h˜ρiU ⊗ U − h˜σ

i (6.6.12)

6.6. APPLICATION TO FLUIDS 289

where ˜σ

is given by

˜σ

= −

′

(τ) ⊗ v

′

(τ)δ(x − x

(τ))

−

j6=i

(τ) − x

(τ)) ⊗ f

(τ)

δ (x − (1 − λ)x

(τ) − λx

(τ)) dλ.

(6.6.13)

The ensemble average in (6.6.12) can be replaced or supplemented by spatial average (or

spatial-temporal average, as is done in HMM):

∆t) =

|ω|

˜σ

(x, nδτ)dx. (6.6.14)

Here ω is the (time-dependent) MD simulation box, |ω| is the volume of ω.

There is a basic diﬀerence between HMM and the seamless algorithm on how stress

is obtained from MD. In HMM, at each macro time step, a constrained MD is performed

and the stress is then computed following the dynamics. During the MD simulation,

the matrix A in (6.6.10) is ﬁxed at the value given by the macro state at that macro

time step. Usually, the above formula is also averaged over time to reduce the statistical

ﬂuctuations. In the seamless algorithm, however, (6.6.10) as well as the MD equations

are solved simultaneously with the macro model, and the data are exchanged at every

time step. Thus the matrix A changes at every step. But this change is very slow, due

to the fact that

∆t is smaller by a factor of M than th e time step ∆t used in HMM.

Example: The driven cavity ﬂow. Next we present some results of the seamless

algorithm for the driven cavity ﬂow. These results are taken from [29]. Results for

HMM are quite similar. We will pay special attention to the eﬀects of the ﬂuctuations

that are intrinsic to this type of algorithms. We consider two types of ﬂuids: The ﬁrst

is composed of simple particles interacting via the Lennard-Jones (LJ) potential. The

second is a polymer ﬂuid which at the microscale is modeled by the bead-spring model

described earlier. Under normal conditions, the LJ ﬂuid is approximately Newtonian

(i.e. the stress and the rate of strain have a linear relationship) and the macro ﬂow

behavior can be accurately described by the Navier-Stokes (NS) equation. Therefore, we

will regard th e solution of the Navier-Stokes equation as the exact solution and use it as

a benchmark for the multiscale method. The d etails of the numerical parameters can be

found in [29].

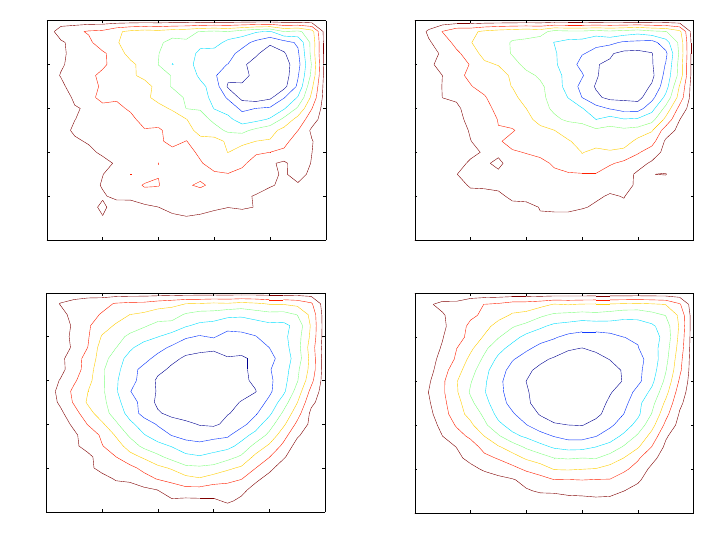
The numerical results for the LJ ﬂuid are shown in Fig. 6.8. The ﬁrst column of the

ﬁgure shows the instantaneous streamlines obtained from the seamless multiscale method

290 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

at several times. As a comparison, in the second column we show the numerical results of

the Navier-Stokes equation at th e same times. The parameters used in the Navier-Stokes

equation are measured from separate MD simulations of the LJ ﬂuid at the same density

and temperature (ρ = 0.81, µ = 2.0 in atomic units). From the ﬁgure we see that the

results of the multiscale method agree very well with the solution of the Navier-Stokes

equation.

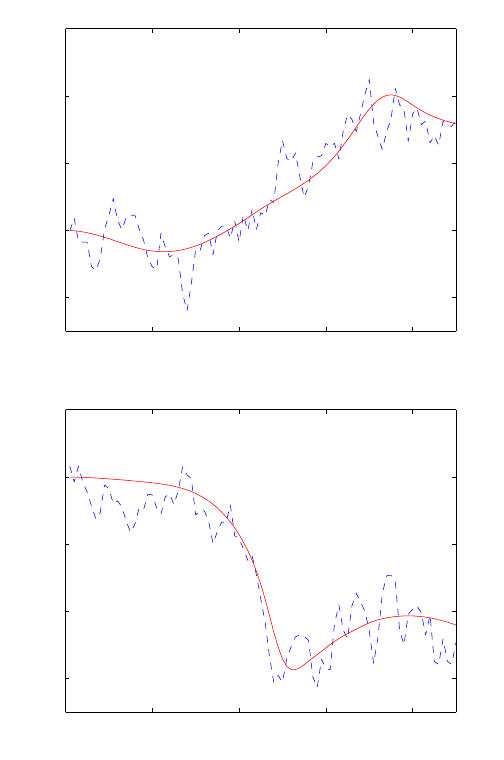
To further assess the performance of the seamless method , we show in Fig. 6.9 the

x-component of the velocity as a function of time at two locations. The dashed curves

are the solution of the seamless method. As a comparison, we also plot the solution

of the Navier-Stokes equation (smooth solid curves). From the ﬁgures we see that the

major diﬀerence of the two results is the ﬂuctuation in the solution of the multiscale

method. This is to be expected and is due to the statistical ﬂuctuations in the stress

tensor computed from MD. This is indeed a major diﬃculty for such multiscale methods.

It can be improved in various ways, e.g. by employing ensemble average (i.e. many

MD replica associated with each grid point), using larger MD system (consequently the

instantaneous stress will be averaged over larger space, see (6.6.14)), or by reducing the

macro time step (see the next example). Apart from the ﬂuctuations, the multiscale

result follows closely the solution of the Navier-Stokes equation.

Next we consider polymer ﬂuids. The MD system at each grid point contains 1000

polymers; each polymer has 12 beads. The density of the beads is 0.81; the MD time

step is 0.002 (in atomic units). All the other parameters are the same as in the previous

example for the LJ ﬂuid. The numerical results are shown in Fig. 6.10. In this example,

two diﬀerent macro time steps are used:

∆t = 0.5 and

∆t = 0.25. The results are

shown in the two columns respectively. Comparing the two solutions we see that their

overall b eh avior agrees very well. We also see that the solution obtained using the smaller

macro time step (the right column) has less ﬂuctuations. We can understand this in the

following way. In the seamless method, the stress tensor is implicitly averaged over time.

Given a macro time T , the MD simulation in the seamless algorithm is carried out for a

period of T δτ/

∆t in the clock of the macro-solver; therefore reducing the macro time step

∆t while keeping the micro time step δτ ﬁxed yields a longer MD simulation. Hence the

numerical result has less statistical error. This is similar to HMM in which the statistical

error can be reduced by increasing the value of the parameter M, the number of MD

steps in one macro time step. This example shows that in the seamless algorithm, the

6.7. STABILITY, ACCURACY AND EFFICIENCY 291

same eﬀect can also be achieved by reducing the macro time step. The diﬀerence is that

in HMM, time average is done explicitly whereas in the seamless method, this is d one

implicitly.

x/L

z/L

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

x/L

z/L

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

x/L

z/L

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

x/L

z/L

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Figure 6.8: Streamlines of a Lennard-Jones ﬂuid in the driven cavity ﬂow at diﬀerent

times: t = 7.5 × 10

, 1.0 × 10

, 1.25 × 10

, 2.25 × 10

(in atomic units, see text) from

top to bottom. The left column is the result of the seamless multiscale method, and the

right column is the numerical solution of the Navier-Stokes equation.

6.7 Stability, accuracy and eﬃciency

Error control for multiscale methods presents a new challenge to numerical analysis,

particularly for problems involving multi-physics. Since multiscale methods are relatively

new, and their errors typically involve several diﬀerent contributions, error analysis is very

much needed for understanding basic issues such as stability, accuracy and eﬃciency.

292 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

0 0.5 1 1.5 2

x 10

−0.2

0.2

0.4

0.6

0 0.5 1 1.5 2

x 10

−0.6

−0.4

−0.2

0.2

Figure 6.9: The x-component of the velocity at the location (1000, 1600) (upper panel)

and (1500, 500) (lower panel) as a function of time. The smooth solid curves are the

solution of the Navier-Stokes equation; the d ashed curves are the solution of the seamless

multiscale method.

6.7. STABILITY, ACCURACY AND EFFICIENCY 293

x/L

z/L

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

x/L

z/L

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

x/L

z/L

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

x/L

z/L

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Figure 6.10: Streamlines of a polymer ﬂuid in the driven cavity ﬂow at diﬀerent times:

t = 7.5 ×10

, 1.0 ×10

, 1.25 ×10

, 2.0 ×10

from top to bottom. The left column is the

result of the seamless multiscale method with the macro time step ∆

′

t = 0.5; the right

column is the result of the multiscale method with a smaller macro time step ∆

′

t = 0.25.

294 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

To begin with, what should we take as the exact or reference solution, to be com-

pared with the numerical solution of a multiscale method? In general, we should not take

the detailed solution of the microscopic problem as the reference solution, since approx-

imating that would require solving the full microscopic problem, and therefore defeat

the whole purpose. For type B problems, since we are only interested in the macroscale

behavior of the solutions, we can take Qu

as the reference solution, where u

is the

solution to the microscopic model, and Q is the compression (or projection) operator

that maps a microscopic state to a macroscopic state. In practice, in order to get explicit

analytical results ab out the behavior of the error, we have to limit ourselves to situations

where we have explicit control of Qu

. These are situations for which limit theorems are

available. These limit theorems allow us to approximate Qu

U, the solution to an

eﬀective macroscale model.

6.7.1 The heterogeneous multiscale method

The basic idea, as was explained in [18], is to compare the HMM solution with the

solution of the selected macroscale solver for the eﬀective macroscale model. Their dif-

ference is caused by an additional error in the HMM solution due to the error in the data

estimation process. This new error term is called the HMM error, denoted by e(HMM).

We will assume that both the HMM and the macro-solver for the eﬀective macroscale

model can be expressed in the form

n+1

HMM

= U

HMM

+ ∆tF

HMM

, U

n−1

HMM

, ···) (6.7.1)

n+1

+ ∆t

F (

n−1

, ···) (6.7.2)

Note that

||Qu

− U

HMM

|| ≤ ||Qu

−

U|| + ||

−

U|| + ||U

HMM

−

|| (6.7.3)

where

U is the solution of the macroscale model,

is th e numerical solution to the

eﬀective macroscale model computed using (6.7.2), U

hmm

is the HMM solution. The ﬁrst

term on the right hand side of (6.7.3) is due to the error of the eﬀective model; the second

term is due to the error in the macroscale solver; the third term is the HMM error, due

to the error in the estimated data. Normally we expect that estimates of the following

6.7. STABILITY, ACCURACY AND EFFICIENCY 295

type hold:

||Qu

−

U|| ≤ Cε

(6.7.4)

U −

|| ≤ C(∆t)

(6.7.5)

where k is the order of accuracy of the macro-solver. In addition, deﬁne

e(HMM) = max

F (U

, U

n−1

, ···) − F

, U

n−1

, ···)k (6.7.6)

Then under general stability conditions, one can show that [18]:

||U

HMM

−

|| ≤ Ce(HMM) (6.7.7)

for some constant C. Therefore, we have

||Qu

− U

HMM

|| ≤ C(ε

+ (∆t)

+ e(HMM)) (6.7.8)

The key in getting concrete error estimates and thereby giving guidelines to designing

multiscale methods lies in the estimation of e(HMM). This is speciﬁc to each problem.

Let us illustrate this general strategy using the example (6.5.1). Note that in the

limit as ε → 0, one expects y to be close to ϕ(x), and hence the eﬀective dynamics for

the slow variable x is given by

d¯x

= f(¯x, ϕ(¯x)) = F (¯x) (6.7.9)

In fact it can be easily shown that if we denote by (x

, y

) the solution of (6.5.1) and if

(0) = ¯x(0), then for any ﬁxed T > 0, there is a constant C

independent of ε, such

that

(t) − ¯x(t)| ≤ C

ε. (6.7.10)

if t ≤ T . This is (6.7.4) for the present example.

Next, let us pick the forward Euler as the macro solver. If we use it to solve the

eﬀective model with time step size ∆t and if we denote the numerical solution by {¯x

then we have

|¯x(t

) − ¯x

| ≤ C

∆t (6.7.11)

if t

≤ T . This is (6.7.5) for the present example.

296 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

The last component is to estimate the HMM error. We can express HMM as:

n+1

= x

+ ∆t

f(x

) (6.7.12)

for some function

f dep ending on the details of the HMM procedure. Let us assume that

the microscale problem is solved using forward Euler with time step δt for M steps and

the last value is used as the estimated force for the macro solver, i.e.

f(x

) = f (x

, y

n,M

then it is a simple matter to prove [17]:

e(HMM) = |

f(x

) − F (x

)| ≤ C|y

n,M

− ϕ(x

)| ≤ C



1 −

δt



δt

(6.7.13)

Here the ﬁrst term on the right hand side accounts for the relaxation error for the fast

variable, the second term accounts for the error in the micro-solver.

Putting all three components together, we have, for t

≤ T ,

) − x

| ≤ C

ε + ∆t +



1 −

δt



δt

(6.7.14)

In the general case when k-th order stable macro and micro solvers are used, we have

[17]:

) − x

| ≤ C

ε + ∆t





δt







δt



ℓ

(6.7.15)

where k and ℓ are the order of accuracy for the macro and micro solvers respectively.

A(λδt) is the ampliﬁcation factor of the microscale solver for the ODE ˙y = −λy.

This is what we get if we follow the standard procedure for analyzing HMM, and they

hold as long as {y

n,0

} are bounded. However, if we take y

n,0

= y

n−1,M

, then (6.7.13) can

be improved to [20]

e(HMM) ≤ C

ε∆t

Mδt

+ ∆t



1 −

δt



δt

. (6.7.16)

and similar results can be obtained when higher order macro and micro solvers are used.

In the same fashion, for stochastic ODEs (6.5.13), one can show that

sup

t≤T

E|x

(t) − ¯x(t)| ≤ C

√