Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

6.7. STABILITY, ACCURACY AND EFFICIENCY 297

where ¯x is the solution to the limiting equation discussed in Section 6.5. If we use the

reinitialization y

n,0

= y

n−1,M

in HMM, we have, under suitable conditions [22, 20]:

e(HMM) ≤ C

ε∆t

Mδτ



δτ



ℓ

. (6.7.17)

sup

t≤T

E|x

HMM

(t) − x

(t)| ≤ C

√

ε +

ε∆t

Mδτ



δτ



ℓ

+ ∆t

. (6.7.18)

Here k and ℓ are the (strong) order of the macro and micro-solvers, respectively.

Error analysis of this type has also been carried out for the ﬁnite element HMM

applied to elliptic homogenization problems [28]. The structure of the error is very similar

to what we just discussed. The parabolic homogenization problem has been analyzed in

[1, 58]. Error analysis and careful numerical studies for the hyperbolic homogenization

problem were presented in [10].

Error analysis of HMM for the case when the eﬀective macroscale model is stochastic

has been considered in [40, 39, 57].

Examples with discrete microscale models were considered in [21]. The microscopic

models can either be molecular dynamics or kinetic Monte Carlo methods. The macroscale

model considered in [21] was gas dynamics or general nonlinear conservation laws. It was

proven in [21] that e(HMM) consists of three parts: the relaxation error, the error due

to the ﬁnite size of the simulation box for the microscale model, and the sampling error.

Clearly as the system size increases, the ﬁnite size eﬀect decreases but the relaxation

error increases. Therefore this result gives some suggestions on how to choose the size of

the domain and the duration for the microscale simulation. Unfortunately there are very

few explicit results on the dependence of these errors on the box size. All known results

are proved for lattice models. We refer to [21] for a discussion of this issue.

These examples are admittedly simple, compared with the real problems we would

like to handle. However, they do provide crucial insight into the structure of the error,

and they give suggestions on the magnitude of each contribution.

6.7.2 The boosting algorithm

In principle, we should be able to develop a similar framework for the error analysis of

the seamless algorithm. However, this program has not yet been implemented. Therefore

298 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

as in [29], we will focus on the simple examples of ODEs and SDEs discussed in Section

6.5. Denote by x

the numerical solution for the macro variable x and ¯x the solution to

the limiting equation (as ε → 0). For these simple examples, the error for the seamless

algorithm can be understood very simply using the observation mentioned earlier when

we introduced the seamless algorithm: Instead of viewing the micro- and macro-solvers

with diﬀerent clocks, we can think of them as being running on the same clock, but with

a diﬀerent value of ε that satisﬁes

δτ

∆t

′

(6.7.19)

′

∆t

δτ

ε (6.7.20)

The seamless algorithm can be viewed as a standard algorithm applied to the modiﬁed

problem with a modiﬁed parameter value. The error consists of two parts: The error due

to boosting the p arameter value from ε to ε

′

and the error du e to the numerical solution

of the boosted model. For the stiﬀ ODE (6.2.1), we obtain the following: For any T > 0,

there exists constant C such that, for t ≤ T ,

(t) − ¯x(t)| ≤ C





′

∆t

′

ℓ

∆t





= C

∆t

δτ

ε +



δτ



ℓ

∆t

(6.7.21)

In terms of the parameters entering the HMM algorithm, (6.7.21) can be written as

(t) − x

(t)| ≤ C

ε +

∆t

δτ



δτ



ℓ



∆t



(6.7.22)

This is to be compared with the error for the HMM algorithm given in (6.7.15) and

(6.7.16). We see that the accuracy is comparable.

Let us now consider the S DE (6.5.13). Using δτ/ε =

∆t/ε

′

, we see that (6.5.18) and

(6.5.19) can be rewritten as:

n+1

= y

−

∆t

′

− ϕ(x

)) +

∆t

′

(6.7.23)

n+1

= x

∆tf(x

, y

n+1

) (6.7.24)

6.7. STABILITY, ACCURACY AND EFFICIENCY 299

which can be considered as a standard discretization of (6.5.13) with the parameter value

of ε boosted to ε

′

. Therefore, the error for the seamless algorithm is controlled by [22]:

sup

t≤T

E|x

(t) − ¯x(t)| ≤ C





√

′

∆t

′

ℓ

+ (∆t)





= C

ε∆t

Mδτ



δτ



ℓ

+ (∆t)

(6.7.25)

sup

t≤T

E|x

(t) − x

(t)| ≤ C

√

ε +

ε∆t

Mδτ



δτ



ℓ

+ (∆t)

. (6.7.26)

Compared with (6.7.18), we see that the errors are comparable for this case also.

6.7.3 The equation-free approach

We begin with the stability of the projective integrators for stiﬀ ODEs. This has been

analyzed in [37]. The essence of this analysis is very nicely illustrated by the following

simple calculation presented in [34] in which ideas similar to that of the projective in-

tegrators were also proposed. For the sake of clarity, we will follow the presentation of

[34].

Consider the ODE











= −

y(0) = 1

(6.7.27)

where ε ≪ 1. Consider a composite scheme which consists of m steps of forward Euler

with step size δt followed by one step of forward Euler with step size ∆t, where δt ≪

ε, ∆t ≫ ε.

After one composite step, the numerical solution is given by y

= R

where the

ampliﬁcation factor R

is given by



1 −

δt





1 −

∆t



(6.7.28)

In order for the method to be stable, i.e. |R

| ≤ 1, we simply need

m > −

log



∆t

− 1



log



1 −

δt



∼

δt

log



∆t



(6.7.29)

300 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

The value of ∆t and δt/ε is set by the error tolerance. Therefore as ε → 0, the total cost

for advancing the system over O(1) time interval is O(log(1/ε)), compared with O(1/ε)

if we use forward Euler with the same step sizes. This calculation illustrates nicely the

eﬀectiveness of solving stiﬀ ODEs using both big and small time steps.

Turning to the issue of spatial discretization in the equation-free approach. We will

focus on patch dynamics since it contains features of both the projective integrators and

the gap-tooth scheme. We will restrict our attention to a one dimensional problem and

denote by {x

= j∆x} the macro grid points. Around each grid point, there is a domain

of size H over which the microscopic model is simulated, and there is another domain of

size h on which the microscale variables are averaged to yield the macroscale variables.

Naturally, h ≤ H. Given the values of the macro variables at the grid points, {U

}, the

lifted state is given by [51]

˜u

) =

k=0

k,j

(x − x

)

(6.7.30)

where D

k,j

is some approximations to the derivatives of the macroscale proﬁle at x

, for

example:

2,j

j+1

− 2U

+ U

j−1

∆x

, D

1,j

j+1

− U

j−1

2∆x

, D

0,j

= U

−

2,j

(6.7.31)

Below we will consider the case when d = 2.

Consider the case when the microscale model is the heat equation [51]:

∂

u = ∂

u (6.7.32)

The eﬀective macroscale equation is also a heat equation: ∂

U − ∂

U. Without loss of

generality let j = 0 and let ˜u

= D

0,0

+ D

1,0

x +

2,0

. The solution to the microscale

model after time δt is

δt

˜u

(x) = D

0,0

+ D

1,0

x + D

2,0

(

+ δt) (6.7.33)

Denote by A

the averaging operator over the small domain (of size h), we have

δt

= A

δt

˜u

(x) = D

0,0

+ D

2,0

δt +

2,0

= U

+ D

2,0

δt (6.7.34)

Simple ﬁrst order extrapolation gives the familiar scheme:

n+1

= U

+ ∆tD

2,0

(6.7.35)

6.7. STABILITY, ACCURACY AND EFFICIENCY 301

as was shown in [51]. This is both stable and consistent with the heat equation, which

is the right eﬀective model at the macroscale.

Now let us turn to the case when the microscale model is the advection equation

∂

u + ∂

u = 0 (6.7.36)

In this case, we have

δt

˜u

(x) = D

0,0

+ D

1,0

(x − δt) +

2,0

(x − δt)

(6.7.37)

Hence,

δt

= A

δt

˜u

(x) = D

0,0

−D

1,0

δt+

0,0

δt

0,0

= U

−D

1,0

δt+

0,0

δt

(6.7.38)

Simple ﬁrst order extrapolation yields:

n+1

= U

+ ∆t(−D

1,0

δtD

2,0

) (6.7.39)

Since δt ≪ ∆t, the last term is much smaller than the other terms, and we are left

essentially with the Richardson scheme:

n+1

= U

− ∆tD

1,0

(6.7.40)

This is unstable under the standard time step size condition that ∆t ∼ ∆x, due to the

central character of D

1,0

There is also a problem of consistency. Assuming that the eﬀective macroscale model

is a 4th order PDE. Without knowing this explicitly, the lifting operator may stop short

of using any information on the 4th order derivatives, which leads to an inconsistent

scheme. These issues are discussed in [31].

These examples are very simple but they illustrate a central diﬃculty with the bottom-

up approach for multiscale modeling: Since the microscale model is only solved on small

domains for short times, it does not have enough inﬂuence on the overall scheme to bring

out the characters of the macroscopic process. Therefore the overall scheme does not

encode enough information about the nature of the macroscale behavior. In particular,

there is no guarantee of stability or consistency for such an approach.

These problems are ﬁxed in a subsequent version of patch dynamics proposed in [66].

In this version, one assumes a macro model of the form

∂

U = F (U, ∂

U, ··· , ∂

U, t) (6.7.41)

302 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

to begin with, and selects a stable “method-of-lines discretization” of this macro model:

∂

= F (U

, D

(U), ··· , D

(U), t) (6.7.42)

Here D

(U) is some suitable ﬁnite diﬀerence discretization of ∂

U. For example, for

advection equation, one should use some one-sided discretization. The operator D

then used in the lifting operator:

¯u

(x, t

) =

k=0

(

)

(x − x

)

, x ∈ [x

−

, x

] (6.7.43)

The idea here is to use a stable macro-solver to guide the construction of the lifting

operator. This version of the patch dynamics does overcome the diﬃculties discussed

above. However, it has also lost its original appeal as an approach that does not require

a preconceived form of the macroscale model. It now has the shortcomings of HMM, but

unlike HMM, it uses the macro-solver indirectly, through the lifting step. This adds to

the complexity of the lifting operator, without any obvious beneﬁts in return. Indeed in

this new version, the reinitialization process not only has to take into account consistency

with the local values of the macro variables (which is the only requirement in HMM),

but also some charateristics of the unknown macroscale model, such as the order of the

eﬀective macroscale PDE, the direction of the characteristic ﬁelds if the macroscale model

happens to be a ﬁrst order PDE. The most unsettling aspect is that we do not know what

else n eeds to be taken into account. This seems to be an issue for any kind of general

bottom-up strategy.

6.8 Notes

Memory eﬀects and time scale separation

Much of the present chapter assumes that there is a separation between the time scale

for the coarse-grained variables and the time scale for the rest of the degrees of freedom.

In many situations, particularly when analyzing the dynamics of macromolecules, it is

unlikely that such a time scale separation exists, yet it is still very desirable to consider

a coarse-grained description. In this case, the dynamics of the coarse-grained variables

should in general have memory eﬀects, as suggested by the Mori-Zwanzig formalism. How

to handle such memory eﬀects in practice is an issue that should receive more attention.

6.8. NOTES 303

Top-down vs. bottom-up strategies

An ideal multiscale method is one that relies solely on the microscale model, without

the need to make a priori assumptions about the form of the macroscale model. Clearly

such a strategy has to be a bottom-up strategy. Unfortunaltey, until now, there are no

such reliable, ideal strategies that are of general interest. Several candidates have been

proposed. The equation-free approach is one possibility. Another possible approach is

the renormalization group methods proposed by Ceder and Curtarolo [14]. There the

idea is to perform systematic coarse-graining to ﬁnd the eﬀective Hamiltonian at large

scales. This is certainly an attractive strategy. But it is not clear how widely applicable

this is. For example, it is not clear how to take into account dissipative processes such

as heat conduction and viscous dissipation.

As we explained earlier, HMM is an example of a top-down strategy. As such, it

does represent a compromise between idealism and practicality. In some sense, it is the

most straightforward way of extending the sequential multiscale strategy to a concurrent

setting.

The ﬁber bundle structure

The philosophy used in HMM and the seamless algorithm can be better appreciated

if we formulate the multiscale problems using a ﬁber bund le structure, in which the local

microstructure is represented by the ﬁbers. The relevance of the concept of ﬁber bundles

was noted in [18, 20]. The systematic treatment was presented in [26]. It is not clear

that there is any real substance in such a viewpoint. But it is sometimes a convenient

way to think about t his class of multiscale problems. In addition, it gives rise to some

interesting models (see [26]).

We start with a simple example. Consider the nonlinear homogenization problem:

∂

= ∇ · (a(u

, x,

)∇u

) (6.8.1)

Here a(u, x, z) is a smooth and uniformly positive deﬁnite tensor function, which is

periodic in z with period Γ. For this problem, the homogenized equation takes the form:

∂

U = ∇ · (A(U, x)∇U), (6.8.2)

where

A(U, x) =

|Γ|

a(U, x, z)(∇

χ(z; U, x) + I) dz. (6.8.3)

304 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

Here I is the identity matrix and χ(z; U, x) is the solution of

∇

· (a(U, x, z)(∇

χ + I)) = 0 in Γ (6.8.4)

with periodic boundary condition.

Intuitively, we can describe the behavior of the solution as follows. At each point x,

(x) is approximated closely by the value of U(x), the microstructure of u

is locally

described by χ, the solution to the cell problem (6.8.4). χ is parametrized by (U, x) and

is a function over Γ. We can think of χ as being the ﬁber over x that describ es the local

microstructure.

Another example is the Cauchy-Born rule discussed in Chapter 5. Here the macroscale

behavior is the large scale deformation of the material, the microstructure is the local

behavior of the crystal lattice at each point. It is more interesting to look at the case

of complex lattices. Roughly speaking, Cauchy-Born rule suggests the following picture

about the deformation of the material: The underlying Bravais lattice undergo es smooth

deformation, described by the Cauchy-Born nonlinear elasticity model. The shift vectors

, p

, ··· , p

), which describe the local microstructure (within each unit cell), minimize

the function W (A, p

, p

, ··· , p

) where A is given by the deformation gradient for the

Bravais lattice at the point of interest. Here the microstructure is parametrized by A

and is a function of the indicies for the shift vectors. The position of the shift vectors

can undergo bifurcations, as is the case for structural phase transformation.

This last example becomes more interesting when the atomistic model is an electronic

structure model, with the electronic structure playing the role of the internal structure

(the shift vectors). In this case, the problem becomes very similar to the homogenization

problem discussed in the ﬁrst example, with the local electronic structure being the ﬁber

that describes the local microstructure.

To explore the ﬁber bundle structure further, let us note that there are two ﬁber

bundles involved (see Figure 6.11): The ﬁrst is a ﬁber bundle in the space of indepen-

dent variables, for which the macroscale space-time domain of interest is the underlying

base manifold, called the domain base manifold, and the domains for the additional fast

variable z which describes the local microstructure are the ﬁbers. The second is a ﬁber

bundle that parametrizes the microstructure. The base manifold, the state base manifold,

is the space of the parameters for the microstructure (e.g. the cell problem). The ﬁbers

are the space of functions over the ﬁbers in the ﬁrst ﬁber bundle.

A ﬁber bundle model generally consists of the following three components:

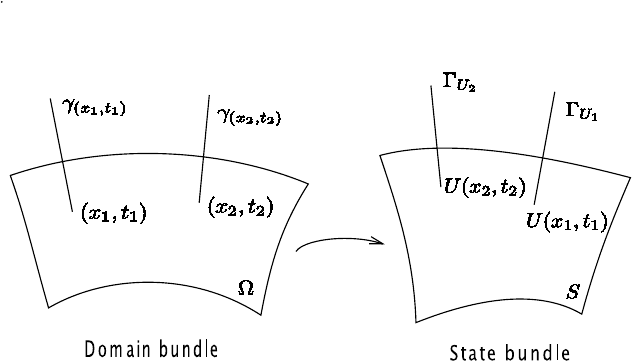
6.8. NOTES 305

Figure 6.11: Fiber bu ndle structure.

1. A macroscale model

L(U; D(U)) = 0. (6.8.5)

Here U = U(x) is a mapping from the domain base manifold Ω to the state base

manifold S. D is the data that depends on the microstructure.

2. The cell problem, which is a microstructure model over the ﬁbers for any x ∈ Ω:

L(u; U(x)) = 0. (6.8.6)

Here U(x) enters as parameters (or constraints) for the microscale model.

3. A relation that speciﬁes the missing input to the macroscale model in terms of the

solutions to the microstructure model:

D(U) = D(U, u(·; U)). (6.8.7)

This complex language simply says that the cell problems are parametrized by U and

the solutions to the cell problems give the missing data in the macro model.

For the homogenization example, the ﬁrst component is given by (6.8.2). The second

component is given by (6.8.4). The third component is given by (6.8.3).

This structure is useful in at least two ways. The ﬁrst is that it gives us a way of

thinking about the underlying mathematical structure for the problems handled by HMM

306 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

and the seamless algorithm. The second is that it yields very interesting models. For

example, in t he ﬁber bundle mo d els, the microstructure is usually slaved by the macro

state of the system. This is analogous to the Born-Oppenheimer model in ab init io

molecular dynamics. One can also formulate the analog of the Car-Parrinello model by

introducing relaxational dynamics for the ﬁbers. This yields interesting models when

applied to the examples discussed above. We refer to [26] for details and additional

examples.