Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

6.3. THE HETEROGENEOUS MULTISCALE METHOD 267

We can write down the HMM procedure formally as follows. At each macro time

step:

1. Given the current state of the macro variables U

, reinitialize the micro-variables:

n,0

= RU

(6.3.8)

2. Evolve the micro variables for some micro time steps:

n,m+1

= S

δt

n,m

; U

), m = 0, ··· , M − 1; (6.3.9)

3. Estimate D:

= D

n,0

, u

n,1

, ··· , u

n,M

); (6.3.10)

4. Evolve the macro-variables for one macro time step using the macro-solver:

n+1

= S

∆t

; D

) (6.3.11)

Here R is some reconstruction operator which plays the same role as the interpolation

or prolongation operators in the multi-grid method, S

δt

is the micro solver, which also

depends on U

through the constraints, as indicated. D

is some data processing oper-

ator which in general involves spatial/temporal/ensemble averaging. This is sometimes

referred to as the data estimator. Finally S

∆t

is the macro solver.

For dynamic problems, there are two important time scales that we need to consider.

The ﬁr st, denoted by t

, is the time scale for the dynamics of the macro-variables. The

second, denoted by τ

, is the relaxation time for the microscopic model. We will need to

distinguish two diﬀerent cases. The ﬁrst is when the two time scales are comparable, i.e.

∼ t

. In this case, from the viewpoint of numerical eﬃciency, there is not much room

to play with as far as time scales are concerned. We just have to evolve the microscale

model along with the macroscale model. The second case is when τ

≪ t

. This is the

case we will focus on. The general guideline in this case is:

1. Choose ∆t to accurately resolve the t

time scale.

2. Choose M such that Mδt covers suﬃciently the τ

time scale to allow equilibration

to take place in the micro model.

Next we consider an example in some detail.

268 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

6.3.2 Simulating gas dynamics using molecular dynamics

Instead of using kinetic theory as in kinetic schemes, we will discuss how to perform

gas dynamics simulation using molecular dynamics models. It is not clear at this p oint

how relevant this is in real applications. We will simply use it as an example to illustrate

HMM.

The microscale model is molecular dynamics, which we will write as

= v

, m

(6.3.12)

Here f

= −∇

(|x

− x

|) is the force on the j-th atom from the k-th atom. For

simplicity, we have assumed that there is only two-body interaction. First of all, recall

that if we deﬁne

˜ρ(x, t) =

δ(x − x

(t)), (6.3.13)

m(x, t) =

(t)δ(x − x

(t)),

E(x, t) =

(t)|

δ(x − x

(t))

(

i6=j

(|x

(t) − x

(t)|))δ(x − x

(t)) (6.3.14)

then we have

∂

˜ρ + ∇

m = 0, (6.3.15)

∂

m + ∇

· ˜σ = 0,

∂

E + ∇

J = 0

where ˜σ and

are deﬁned in terms of {x

, v

} (see Section 4.2). These are the analog

of the conservation laws used in deriving the continuum mo d els of gas dynamics, and is

our starting point for coupling the macroscale and microscale models.

Since the macroscale model is a system of conservation laws, it is natural to use

the ﬁnite volume method as the macro solver. There are many diﬀerent versions of the

ﬁnite volume methods (see for example [55]). We will choose the one that uses the least

amount of information about the details of th e model, since we do not know much about

6.3. THE HETEROGENEOUS MULTISCALE METHOD 269

the details of the model. For example, central type of schemes such as the Lax-Friedrichs

scheme are preferred over schemes that rely on characteristic decomposition such as the

Roe scheme. We will pick the Lax-Friedrichs scheme as the macro solver:

n+1

j+1/2

+ U

j+1

−

∆t

∆x



j+1

− F



. (6.3.16)

The data to be estimated are the ﬂuxes. This is done by performing MD simulation at

places where the numerical ﬂuxes are needed.

The Lax-Friedrichs scheme has another feature that helps to simplify the data esti-

mation step – it is deﬁned on a staggered grid. Consequently, in order to estimate F

we need to set up an MD with the constraints that the average mass, momentum and

energy densities be equal to U

. This can be achieved simply by initializing the MD with

such a constraint and then using the periodic boundary condition. Note that they are

conserved quantities of the MD.

As the MD proceeds, we extract the needed data, namely ˜σ and

by performing

statistical averaging using the Irving-Kirkwood type of formulas discussed in Section 4.2.

Some typical results are shown in F igure 6.3.2. One can see that after a limited number

of steps, the estimated values of ˜σ and

have already reached reasonable accuracy,

independent of how large the macroscale system is.

Shown in Figure 6.3.2 is an example of the numerical results produced using the HMM

just described, for a slightly diﬀerent application, namely one dimensional thermoelas-

ticity. This is a Riemann problem mimicking the setup of a shock tube problem, i.e. th e

macroscale initial condition is piecewise constant, U

= U

in the left half of the domain

and U

= U

in the right half of the domain. If we neglect viscous and thermal dissipa-

tion, then the macroscale solution should be self-similar. This fact is used in the ﬁgure:

The MD results are computed for a small system and for a short time and then rescaled

in space and time in order to be compared with HMM results which were computed for

much larger systems and much longer time.

6.3.3 The classical examples from the HMM viewpoint

Let us now reexamine the examples in Section 6.1 from an HMM perspective.

The Born-Oppenheimer dynamics can be viewed as a special case of HMM in which

the macro solver is the molecular dynamics algorithm chosen for (6.1.8), the data to

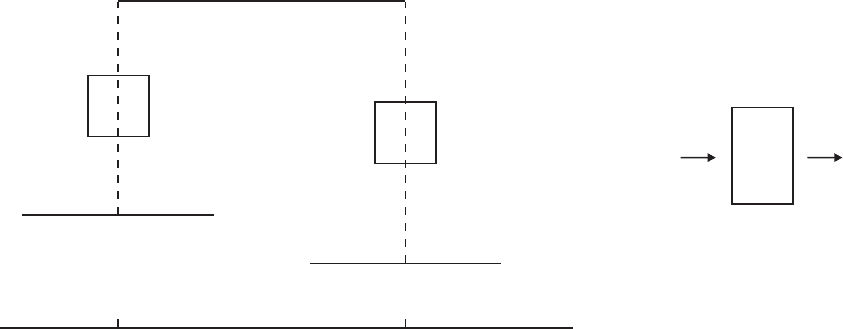
270 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

j+1

F(U

)

F(U

)

F(U

j+1

)

j+1/2

Figure 6.4: Illustration of the HMM procedure for capturing the macroscopic behavior

of gas dynamics using molecular dynamics. This setup takes advantage of the staggered

grid used in the macroscale solver. Courtesy of Xiantao Li.

be estimated is the force acting on the nuclei, and data estimation is done through an

iterative algorithm for the electronic structure model. For the local QC, the macro solver

is the linear ﬁnite element method, the data to be estimated is the energy associated

with the trial function or the forces on the representative atoms. Data estimation can be

done either using the Cauchy-Born rule or the cluster-summation rule. For the kinetic

scheme, the macro solver is the ﬁnite volume method. The data to be estimated are the

numerical ﬂuxes. Data estimation is done by solving the kinetic equation locally around

the point of interest.

Considering the fact that these algorithms are proposed for drastically d iﬀerent ap-

plications, this uniﬁed view is quite interesting. It also oﬀers some substances:

1. As will be discussed below (see Section 6.7), the HMM framework provides a general

strategy for analyzing the stability and accuracy of multiscale methods. This can be

used to analyze the algorithms discussed in Section 6.1. One example, the analysis

of the local QC, is carried out in [27] using this viewpoint.

2. HMM provides an alternative perspective on how to improve these existing meth-

ods. For example, if we are interested in developing high order kinetic schemes, we

6.3. THE HETEROGENEOUS MULTISCALE METHOD 271

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1

−15

−10

−5

x 10

−3

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1

−0.1

−0.05

0.05

0.1

0.15

0.2

0.25

0.3

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1

−0.012

−0.01

−0.008

−0.006

−0.004

−0.002

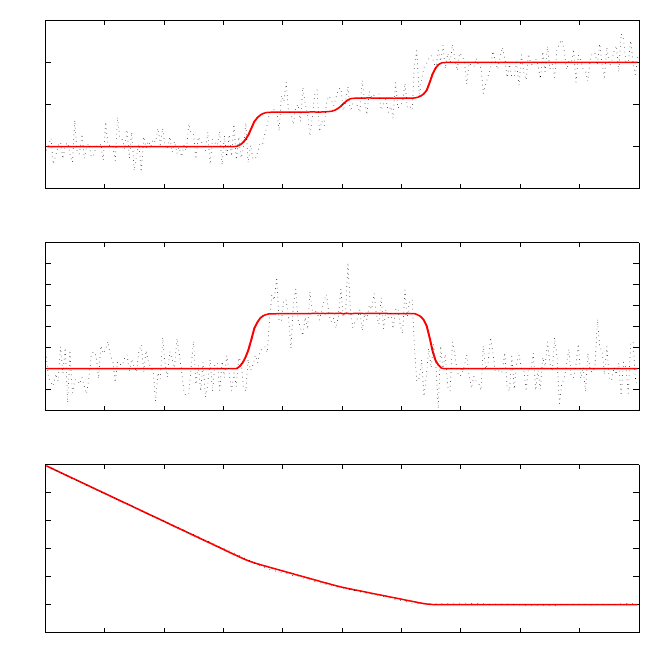
Figure 6.5: Comparison of the numerical solutions obtained using HMM and direct MD. Solid

line: computed solution; dashed line: full atom simulation (one realization). Top: strain;

middle: velocity; bottom: displacement.

272 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

might start with a high order macro solver and solve the kinetic model to high or-

der accuracy. This may not be that diﬀerent from what experts in kinetic schemes

would do anyway. But it does make the ideas a bit more systematic.

There is one very n otable exception though, and that is the Car-Parrinello molecular

dynamics (CPMD). It is of a rather d iﬀerent ﬂavor from that of the HMM we have

discussed so far. The coupling used in CPMD is much more seamless than the “multi-

grid” style of coupling used in HMM, which requires going back and forth explicitly

between the macro and micro states. We will return to th is issue later when we discuss

seamless coupling strategies (see Section 6.5).

6.3.4 Modifying traditional algorithms to handle multiscale prob-

lems

HMM can also be viewed as a principle for modifying traditional numerical algorithms

for the purpose of handling eﬃciently multiscale problems. To illustrate this point, we will

discuss how to mo d ify the fast multipole metho d to handle multiscale charge distribution.

As was discussed in Section 3.2, the fast multipole method (FMM) is among the most

eﬃcient algorithms for evaluating the Coulomb potential due to a distribution of charges

[43]. Consider the following problem:

(x) =

Ω

(y)

|x − y|

dy (6.3.17)

where q

(y) = q(y, y/ε) and q is a smooth function which is periodic in the second

variable with period I = [0, 1]

and ε ≪ 1. Problems of this type arise in electronic

structure analysis of crystalline materials [25]. Applying FMM directly to the evaluation

of φ

will require a cost of O(ε

−3

), since the smallest boxes used in FMM should resolve

the smallest scale of q

, which is of O(ε). A much more eﬃcient approach is to combine

FMM with HMM [46].

In the spirit of HMM, we select FMM as the macroscale solver, the size of the smallest

boxes in FMM is decided by the size needed to resolve the large scale features of the

charge distribution, not the small scale features. The data that are needed in FMM are

the coeﬃcients of the multi-pole expansion:

k,j

q(y,

)(y − x

k,j

)

6.4. SOME GENERAL REMARKS 273

where (C

k,j

, x

k,j

) =j-th (box, box-center) at the k-th level. These integrals can be ap-

proximately evaluated using, for example:

k,j

≃

k,j

q(y, z)(y − x

k,j

)

dydz

The total cost of this approach is O(1).

6.4 Some general remarks

6.4.1 Similarities and diﬀerences

There are obvious similarities between the extended multi-grid method, HMM and

the equation-free approach.

1. They all have the same objective, namely, developing algorithms that capture

the macroscale behavior of complex systems with the help of the microscopic models,

bypassing empirical macroscopic models, and hopefully, without the need to resolve all

microscopic details.

2. They all use a “multi-grid style of coupling”, namely, the macro and micro variables

are converted back and forth at each macro time step or macro iteration step, even though

somewhat diﬀerent terminologies are used (see Table 6.4.1).

3. They all explore the possibility of restricting the simulation of the microscale model

to small domains (boxes, windows) for short times (or few sweeps).

Moreover, as was mentioned earlier, the basic structure for the extended multi-grid

method is remarkably close to that of the equation-free approach, as can be seen in Table

6.4.1. Note in particular that the purpose of the “evolution” step in the equation-free

approach is to equilibrate.

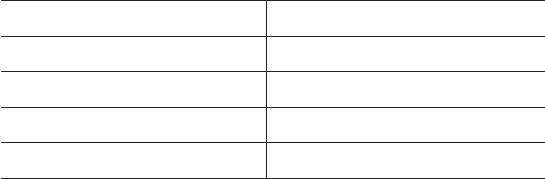
Publisher, could you ﬁx these tables including the references to the tables

in the text?

Macro to micro micro t o Macro

Extended multi-grid interpolation restriction (projection)

HMM reconstruction compression

Equation-free lifting restriction

274 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

Caption: A comparison between the t erminologies used in the extended multi-grid

method, HMM and the equation-free approach.

Extended multi-grid “Equation-free”

Interpolation Lifting

Equilibration Evolution (equilibration)

Restriction (projection) Restriction

Extrapolation

Caption: A comparison between the basic structure of the extended multi-grid method

and the equation-free approach.

There are also some diﬀerences. As was pointed out already, compared with the

multi-grid approach, equation-free uses extrapolation as a way of exploring time scale

separation. Between HMM and equation-free, it is quite clear that at a philosophical level,

HMM is a “top-down” approach, it is more of an “equation-based ” technique, although

the “equation”, i.e., the preconceived form of the macroscale model, is incomplete. In

contrast, equation-free seems to be more of a “bottom-up” strategy. Its purpose was to

set up microscopic simulations on small windows to mimic a simulation over the whole

macroscopic physical domain. One clear example is the gap-tooth scheme in [38] discussed

earlier. The main thrust there was to couple the diﬀerent microscopic simulations on

small boxes in order to mimic a microscopic simulation p erformed over the entire physical

domain, using basically the smoothness of the macro variables.

At a technical level, if we write the eﬀective macroscale model in the form:

∂

U = F ({U}) (6.4.1)

the diﬀerence between HMM and the equation-free approach is that equation-free focuses

on the left hand side and HM M focuses on the right hand side. Here we write F ({U})

instead of F (U) to emphasize that the right hand side can depend on more variables than

the pointwise value of U: For example, it may depend on the gradients of U. Equation-

free can be viewed as a strategy in which the microscale models are used to compute the

approximate value of ∂

U, and this value is used to advance U over macro time steps. In

HMM, however, the ﬁrst question one asks is: What can we say about the structure of

F ({U})? This information is then used to select a macro-solver. For example, in the case

6.4. SOME GENERAL REMARKS 275

when the eﬀective macroscale model is a stochastic diﬀerential equation, then F ({U}) is

a sum of two terms, a drift term and a noise term. HMM treats the two terms separately

[73].

If we do not know anything about the structure of F ({U}), then evaluating F ({U})

is the same as evaluating ∂

U directly. In this case, HMM still provides the ﬂexibility of

selecting a suitable macro solver.

6.4.2 Diﬃculties with the three approaches

Diﬃculties with the multi-grid method

While its general philosophy is very attractive, the algorithmic details for the extended

multi-grid method are sparse. In particular, it is not clear whether Brandt aims at con-

structing linear or sublinear scaling algorithms. The discussions about “small windows”

and “few sweeps” suggest that the goal is to construct sublinear scaling algorithms. But

his insistance on complete generality raises some doubts: Clearly it is not possible to

construct sublinear scaling algorithms that work for general problems.

Diﬃculties with HMM

The most signiﬁcant shortcoming of HMM is that it is based on a preconceived

macroscale model. If the form of the macroscale model is chosen incorrectly, one cannot

expect the resulting HMM procedure to produce accurate results. For example, if the

eﬀective macroscale model should be a stochastic ODE, but one makes the assumption

that it is a deterministic ODE, then the stochastic component of the macroscale solution

will not be captured correctly by an HMM based on such an assumption.

There is a important reason for starting with t he macro-solver: Even for problems for

which we do have a suﬃciently accurate macroscale model, ﬁnding an eﬀective numerical

algorithm for that macroscale model may still b e a signiﬁcant task. Indeed this has been

the focus of the computational mathematics community for more than 50 years. One

example is Euler’s equation in gas dynamics whose solutions typically contain shocks,

i.e. discontinuities [55]. In this case, the numerical algorithms have to satisfy certain

constraints in order to be able to solve Euler’s equation accurately. Obviously this should

also be a concern for multiscale methods.

For practical problems of interest, we often have accumulated some knowledge about

what th e macroscale model should be like. Such information can be used when making

276 CHAPTER 6. CAPTURING THE MACROSCALE BEHAVIOR

assumptions about the macroscale model used in HMM. In cases when one makes a wrong

assumption, one can still argue that HMM produces an “optimal approximation” for the

macroscale behavior of the solution in the class of the models considered. In this sense,

HMM is a way of addressing the following question: What is the best one can do given

the knowledge we have about the problem at all scales?

Diﬃculties with the equation-free approach

There is still some confusion about the basics, namely, the basic philosophy of the

equation-free approach. For this reason, we have carefully followed the original papers in

our presentation above about the equation-free approach. To give an example about the

kind of confusion we are concerned with, let us consider the example of analyzing the free

energy proﬁle of a complex system by computing the probability density of some coarse-

grained variables (see for example [33]). The probability density f = f(q) is assumed to

satisfy a Fokker-Planck equation of the form:

∂

(∂

[D(q)f(q)] − V (q)f(q)) = 0 (6.4.2)

Here q is some coarse-grained variable. Microscopic models are used to precompute the

coeﬃcients D and V . (6.4.2) is then used to ﬁnd the free energy density or for other

purposes. This is a very useful approach, as was demonstr ated in [33, 47] and numerous

other examples. It also extends the standard free energy analysis by allowing a more

general form of the diﬀusion coeﬃcient D. However, from the viewpoint of multiscale

modeling, it is anything but “equation-free”: It is a typical example of the precomputing

(or sequential coupling, see Chapter 1), equation-based technique. It has the standard

merits and diﬃculties of all precomputing techniques. For example, it becomes unfeasible

when the dimension of q is large.

In addition, as we will see later, the original patch dynamics may suﬀer from issues

of numerical instability. To overcome these problems, a new version of the patch dy-

namics has been proposed in which a preconceived macroscale model and a macroscale

solver is used to construct the lifting op erator (see Section 6.7). The original appeal of

the equation-free approach, namely that it does not require knowing much about the

macroscale model, seems to be lost in this modiﬁed version.

In summary, ﬁnding a robust bottom-up approach that does not require making a

priori assumpt ions on the form of the macroscale model is still an open problem. It is

not clear at this stage whether it is possible to have a general approach of this kind and