Weinan E. Principles of Multiscale Modeling
Подождите немного. Документ загружается.

5.3. THE MOVING CONTACT LINE PROBLEM 237
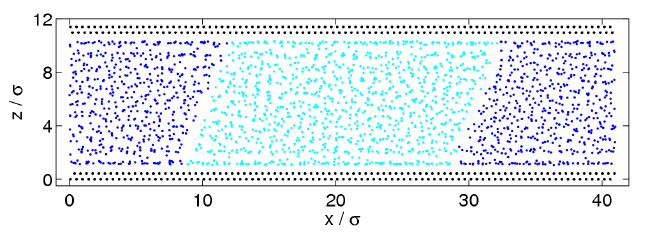
Figure 5.7: An instantaneous configuration of a two-phase fluid system obtained from
molecular dynamics simulation. The system is driven by the motion of the two confining
walls in opposite directions along the x axis.
strength. The simplest way to model the solid walls is to use a few layers of atoms
in a close-packed structure, i.e. the face-centered cubic lattice in the [111] direction,
with some number density ρ
w
. For the purpose of illustration, we will consider only the
particular case when the two fluid p hases have the same density and the same interaction
strength with the solid wall. In this case, we have γ
1
= γ
2
and θ
0
= 90
o
.
Standard techniques of molecular dynamics can be used to bring the system to a
statistical steady state. The friction force along the wall between the fluid and solid
particles can be computed at different values of U. A typical profile of t he friction force
along the wall is shown in Figure 5.8. Notice that the friction force drops sharply in
the fluid-fluid interfacial region. This region is defined as the contact line region. The
average friction force in this region is recorded as the friction force at the contact line,
and is plotted as a function of U in Figure 5.8. Here ε
wf
denotes the value of ε in the
LJ potential for the interaction between the fluid and solid particles. The corresponding
values for the fluid-fluid and solid-solid interaction are equal, and are denoted by ε.
From these results, one can see that the friction law is linear at small values of U,
and becomes nonlinear at large values. The friction force reaches a maximum at certain
critical contact line speed (relative to the wall), then decreases as the speed further
increases. The friction force is smaller for systems with larger solid number densities.
We also see that the critical contact line speed at which the friction force starts to decrease
also becomes smaller for systems with larger solid densities.
The combination of the macroscopic thermodynamic consideration and molecular
238 CHAPTER 5. EXAMPLES OF MULTI-PHYSICS MODELS
0 10 20 30 40 50
0
0.05
0.1
0.15
0.2
x / σ
f / εσ
−3
0 1 2 3 4
0
0.05
0.1
0.15
u
CL
/ στ
−1
f
CL
/ εσ
−3
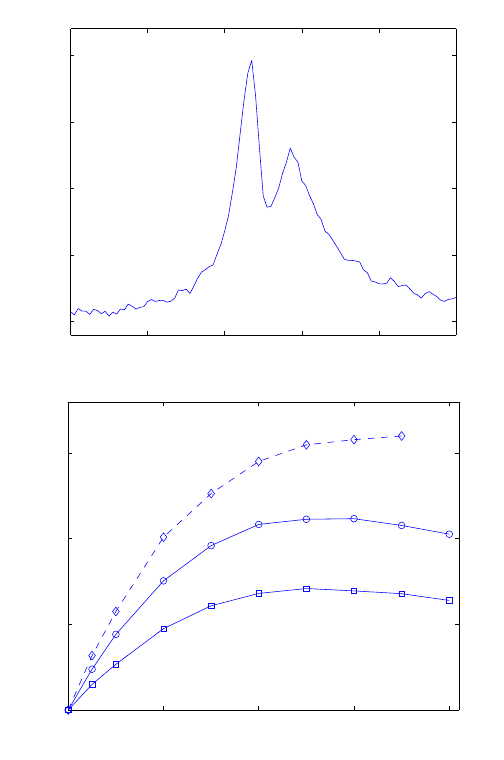
Figure 5.8: Upper panel: a typical profile of the friction force along the solid wall. Lower
panel: friction force in the contact line region versus the slip velocity at the contact
line for different fluid and solid densities as well as different interaction parameters,
ρ
w
= 8ρ
f
, 12ρ
f
for the dashed curve and solid curve respectively; ε
wf
= 0.2ε (diamonds),
ε
wf
= 0.3ε (squares) and ε
wf
= 0.5ε (circles). Here ρ
w
and ρ
f
are t he density of particles
in the wall and liquid phases respectively.
5.4. NOTES 239
dynamics studies allows u s to establish a fairly complete and fairly solid continuum model
for this problem. However, it should also b e noted that the accuracy of such a pro cedur e
relies on the accuracy of the microscopic model. From a quantitative viewpoint, we have
only considered a rather simplistic situation here. For systems of practical interest, it is
usually quite non-trivial to come up with accurate microscopic models.
5.4 Notes
This chapter discusses how multiscale ideas can be used to develop better models,
not just numerical algorithms. The material discussed in the section on polymer fluids
is quite standard and can be found in [3], for example. Ou r presentation follows that of
the review article by Li and Zhang [26]. We only touched up on the situation of dilute
polymer solutions. For more general introduction to polymer structure and dynamics,
we refere to [4, 3, 10, 29].
Clearly the philosophy of coupling the macroscopic model with some description of t he
microscopic constitu ents can be applied to a large variety of problems. We have already
mentioned the example of Car-Parrinello molecular dynamics in which the dynamics of
the nuclei is coupled with a description of the electronic structure. Another interesting
example is the analysis of material failure by coupling a macroscopic model with some
description of the dynamics of the micro damages [43].
Developing continuu m elasticity models from atomistic models has also been a subject
of intensive research. We refer to [1, 7, 17] for more discussions. Using continu um
concepts to study the mechanics of nano-tubes has also attracted a great deal of attention,
see for example [45].
As remarked earlier, the moving contact line problem has often been used to illustrate
the need to develop coupled atomistic-continuum simulation strategies [27, 20, 36]. The
viewpoint adopted here is different: Instead of coupling continuum and atomistic models
on the fly, we demonstrated a sequential coupling strategy in which the needed boundary
conditions were measured beforehand using molecular dynamics. This is possible since
we limited the form of the boundary conditions to some particular class of functions
that depend on very few variables (friction force depends only on the lo cal slip velocity).
The advantage of this approach is that we now have a complete continuum model with
which we can do analysis, not just simulation. It also reveals some physically interesting
240 CHAPTER 5. EXAMPLES OF MULTI-PHYSICS MODELS
quantities such as the three-phase friction coefficient. The disadvantage is that it is
limited to the special forms of constitutive relations we considered. Therefore in some
situations, it may not be adequate. This is an example of the top-down approach, in the
spirit of the heterogeneous multiscale method (HMM) to be discussed in more detail in
the next chapter.
An alternative is the bottom-up approach: One performs extensive MD simulations
and tries to extract the effective continuum model by mining the MD data. In the
context of the moving contact line problem, very careful work on measuring the b ound ary
condition at the contact line region from MD data was rep orted in [32]. Note that the
generality of this approach is also limited by the setup of the MD. S ince the MD performed
by Qian et al. also uses a Couette flow geometry, their boundary conditions are limited
to the form considered here.
Finally, a word about the Huh-Scriven singularity. Although the slip bound ary con-
dition helps to remove this singularity, it should be noted that the no-slip boundary
condition is recovered in the effective macroscopic models at length scales comparable
to the system size [34]. Therefore at the macroscopic scale, the Huh-Scriven singularity
seems to be unavoidable.
Bibliography
[1] M. Arroyo and T. Belytschko, “Finite element methods for the nonlinear mechanics
of crystalline sheets and nanotubes,” Intl. J. Num. Meth. Engrg., vol. 59, pp. 419–
256, 2004.
[2] J. W. Barrat and E. S¨uli, “Existence of global weak solutions to some regularized
kinetic models for dilute polymers,” Multiscale Model. Simul., vol. 6, no. 2, 506–546,
2007.
[3] R.B. Bird, C.F. Curtiss, R.C. Armstrong and O. Hassager, Dynamics of Polymeric
Liquids, Vol. 2: Kinetic Theory, John Wiley, New York, 1987.
[4] R.B. Bird, R.C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids, Vol.
1: Fluid Mechanics, John Wiley, New York, 1987.
[5] T. D. Blake, “Dynamic contact angles and wetting kinetics,” in Wettabili ty, pp .
252–302, ed. John C. Berg, Marcel Dekker, New York, 1993.
[6] T. D. Blake and J. M. Haynes, “Kinetics of liquid/liquid displacement,” J. Colloid
Interface Sci. vol. 30, pp. 421–423, 1969.
[7] X. Blanc, C. Le Bris and P. L. Lions, “From molecular models to continuum me-
chanics,” Arch. Rat. Mech. Anal., vol. 164, pp. 341–381, 2002.
[8] D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, “Wetting and spreading,”
Rev. Mod. Phys., vol. 81, pp. 739–805 , 2009.
[9] R. Car and M. Parrinello, “Unified approach for molecular dynamics and density-
functional theory,” Phys. Rev. Lett., vol. 55, pp. 2471–2474, 1985.
241
242 BIBLIOGRAPHY
[10] M. Doi and S. F. Edwards, The Theory of Polymer Dyn amics, Oxford Science Pub-
lications, 1986.
[11] P. G. de Gennes, “Wetting: statics and dynamics,” Rev. Mod. Phys. vol. 57, pp.
827–863, 1985.
[12] P.-G. de Gennes, F. Brochard-Wyart, and D. Quere, Capillarity and Wetting Phe-
nomena: Drops, Bubbles, Pearls, Waves, Springer-Verlag, 2003.
[13] S.R. de Groot and P. Mazur, Non-Equilibrium Thermodynamics, Dover Publications,
Inc., 1984.
[14] E. B. Dussan V., “On the spreading of liquids on solid surfaces: static and dynamic
contact lines,” Ann. Rev. Fluid Mech. vol. 11, pp. 371–400, 1979.
[15] W. E and P.B. Ming, “Cauchy-Born rule and the stability of the crystalline solids:
static problems,” Arch. Rat. Mech. Anal., vol. 183, pp. 241–297, 2007.
[16] W. E and P.B. Ming, “Cauchy-Born rule and the stability of the crystalline solids:
dynamic problems,” Acta Math. Appl. Sin., Engl. Ser. vol. 23, pp . 529–550, 2007.
[17] G. Friesecke and R. D. James, “A Scheme for the passage from atomic to continuum
theory for thin films, nanotubes and nanorods,” J. Mech. Phys. Solids, vol. 48, pp.
1519–1540, 2000.
[18] C. W. Gardiner, Handbook of Stochastic Methods, 2nd ed., Springer-Verlag, 1997.
[19] M. E. Gurtin, Thermodynamics of Evolving Phase Boundaries in the Plane, Oxford
Mathematical Monographs, Oxford University Press, 1993.
[20] N. Hadjiconstantinou, “Hybrid atomistic-continuum formulations and the moving
contact-line problems,” J. Comp. Phys, vol. 154, pp. 245–265, 1999.
[21] C. Huh and L. E. Scriven, “Hydrodynamic model of steady movement of a
solid/liquid/fluid contact line,” J. Colloid Interface Sci., vol. 35, pp. 85–101, 1971.
[22] X. Guo, J. B. Wang, H. W. Zhang, “Mechanical properties of single-walled carbon
nanotubes based on higher order Cauchy-Born rule,” Int. J. Solids Struct., vol. 43,
pp. 1276–1290, 2006.
BIBLIOGRAPHY 243
[23] D. Jacqmin, “Contact-line dynamics of a diffusive fluid interface”, J. Fluid. Mech.,
vol. 402, pp. 57–88, 2000.
[24] J. Koplik, J. R. Banavar and J. F. Willemsen, “Molecular dynamics of Poiseuille
flow and moving contact lines,” Phys. Rev. Lett., vol. 60, pp. 1282–1285, 1988.
[25] J. Koplik, J. R. Banavar and J. F. Willemsen, “Molecular dynamics of fluid flow at
solid surfaces,” Phys. Fluids A, vol. 1, pp. 781–794, 1989.
[26] T. Li and P. Zhang, “Mathematical analysis of multi-scale models of complex fluids,”
Comm. Math. Sci., vol. 5, no.1, pp. 1–51, 2007.
[27] S.T. O’Connell and P.A. Thompson, “Molecular dynamics-continuum hybrid com-
putations: A tool for studying complex fluid flows,” Phys. Rev. E, vol. 52, no. 6, pp.
R5792–R5795, 1995.
[28] B. Oksendal, Stochastic Differential Equations, 4th ed., Sprin ger, 1995.
[29] H. C.
¨
Ottinger, Stochastic Processes in Polymeric Liquids, Springer-Verlag, Berlin
and New York, 1996.
[30] H. C.
¨
Ottinger, Beyond Equilibrium Thermodynamics, Wiley Interscience, 2005.
[31] T. Qian, X. P. Wang and P. Sheng, “Molecular scale contact line hydrodynamics of
immiscible flows,” Phys. Rev. E vol. 68, pp. 016306-1–0616306-15, 2003.
[32] T. Qian, X. P. Wang and P. Sheng, “Molecular hydrodynamics of the moving contact
line in two-phase immiscible flows,” Commun. Comput. Phys., vol. 1, no. 1, pp. 1–52,
2006.
[33] W. Ren and W. E, “Boundary conditions for moving contact line problem,” Phys.
Fluids, vol. 19, pp. 022101–022101-15, 2007.
[34] W. Ren and W. E, “Hysteresis and effective models for the contact line problem on
heterogeneous surfaces”, preprint, 2010.
[35] W. Ren, D. Hu and W. E, “Continuum models for the contact line problem,” sub-
mitted.
244 BIBLIOGRAPHY
[36] W. Ren and W. E, “Heterogeneous multiscale method for the modeling of complex
fluids and micro-fluidics,” J. Comp. Phys., vol. 204, pp. 1–26, 2005.
[37] B. Schweizer, “ A well-posed model for dynamic contact angles,” Nonlinear Anal.
Theory Methods Appl., vol. 43, pp. 109–125, 2001.
[38] P. A. Thompson and M. O. Robbins, “Simulations of contact-line motion: Slip and
the dynamic contact angle,” Phys. Rev. Lett., vol. 63, pp. 766–769, 1989.
[39] P. A. Thompson and S. M. Troian, “A general boundary condition for liquid flow at
solid surfaces,” Nature, vol. 389, pp. 360–362, 1997.
[40] P. A. Thompson, W. B. Brinckerhoff and M. O. Robbins, “Microscopic studies of
static and dynamics contact angles,” J. Adhes. Sci. Technol., vol. 7, pp. 535–554,
1993.
[41] B. H. A. A. van den Brule, A. P. G. van Heel and M. A. Hulsen, “Brownian con-
figuration fields: A new method for simulating viscoelastic flow,” Macromol. Symp.,
vol. 121, pp. 205–217, 1997.
[42] G. Voth (eds), Coarse-Graining of Condensed Phase and Biomolecular Systems,
CRC Press, Taylor and Francis Group, 2009.
[43] H. Wang, Y. Bai, M. Xia and F. Ke, “Microdamage evolution, energy dissipation
and their trans-scale effects on m acroscopic failure,” Mechanics of Materials, vol.
38, pp. 57–67, 2006.
[44] X. P. Wang and Y. Wang, “The sharp interface limit of a ph ase field model for
moving contact line problem,” Methods and Applications of Analysis, vol. 14, pp.
287–294, 2007.
[45] B. I. Yakobson, C. J. Brabec, and J. Bernholc, “Nanomechanics of carbon tubes:
Instabilities b eyond linear response,” Phys. Rev. Lett., vol. 76, pp. 2511–2514, 1996.
[46] J. Z. Yang and W. E, “Generalized Cauchy-Born rules for elastic deformation of
sheets, plates, and rods: Derivation of continuum models from atomistic models,”
Phys. Rev. B, vol. 74, pp. 184110–184110-11, 2006.
BIBLIOGRAPHY 245
[47] P. Zhang, Y. Huang, P. H. Geubelle, P. A. Klein, K. C. Hwang, “The elastic modulus
of single-wall carbon nanotubes: A continuum analysis incorporating interatomic
potentials,” Int. J. Solids Struct., vol. 39, pp. 3893–3906, 2002.
246 BIBLIOGRAPHY
