Weinan E. Principles of Multiscale Modeling
Подождите немного. Документ загружается.


4.5. NOTES 207
In this case the Hamiltonian matrix has only two parameters: ε
s
, the on-site energy and
t, the hopping element:
H =
ε
s
−t −t
−t ε
s
−t 0
−t ε
s
·
· · ·
0 · · ·
· · −t
−t −t ε
s
(4.4.65)
The eigenvalues and eigenvectors for this matrix can be found by discrete Fourier trans-
form:
ε
k
= ε
s
− 2t cos(ka) (4.4.66)
Ψ
k
=
1
√
N
N/2
X
l=−N/2
e
ikx
l
ϕ
l
(4.4.67)
where l runs over all the integers between −N/2 and N/2, l and k are related to each
other by
k =
2πl
Na
(4.4.68)
k runs over the so-called first Brillouin zone:
−
π
a
< k ≤
π
a
(4.4.69)
The ranges of l and k can be shifted by periods of N and 2π/a respectively, corresponding
to a reordering of the eigenvalues and eigenvectors.
Since each state can accommodate two electrons, one with an up spin and one with a
down spin, only half of the states are filled in the ground state of the system. In addition,
when N is large, the energy gap between the occupied states and the unoccupied states
is very small. Therefore the system behaves like a metal.
4.5 Notes
The main objective of this chapter is to give an overview of how the physical models
at the different levels of detail are like and how they are related to each other. These
208 CHAPTER 4. THE HIERARCHY OF PHYSICAL MODELS
physical models are the main ingredients used in multiscale, multi-physics modeling. This
chapter is also very terse but we hope we have conveyed the main ideas.
From a mathematical viewpoint, a huge amount of work has been done on continuum
models such as models in elasticity theory and fluid dynamics. Some work has been done
on kinetic theory. Much less is done on atomistic and electronic structure models. As we
will see below, this relative lack of understanding for atomistic and electronic structure
models is an essential obstacle for building the foundation of multiscale, multi-physics
modeling.
Understanding the connection between the different models is also a very important
component of multiscale modeling. Here we have illustrated how continuum models of
nonlinear elasticity can be linked to atomistic models through th e Cauchy-Born rule,
and how hydrodynamic equations of gas dynamics can be derived from the Boltzmann
equation. An important topic that we did not discuss is the hydrodynamic limit of
interacting particle systems. We refer the interested reader to [25, 37].
Bibliography
[1] M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press,
New York, 2001.
[2] P. L. Bhatnagar, E. P. Gross and M. Krook, “A model for collision processes in gases.
I. Small amplitude processes in charged and neutral one-component systems,” Phys.
Rev. , vol. 94, pp. 511–525, 1954.
[3] X. Blanc, C. Le Bris and P. L. Lions, “From molecular models to continuum me-
chanics,” Arch. Rational Mech. Anal., vol. 164, pp. 341–381, 2002.
[4] M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Oxford University
Press, 1954.
[5] B.R. Brooks, R.E. Bruccoleri, B.D. Olafson, D.J. States, S . Swaminathan, M.
Karplus, “CHARMM: A program for macromolecular energy, minimization, and
dynamics calculations,” J. Comp. Chem. vol. 4, pp. 187–217, 1983.
[6] R. Car, unpublished lecture notes.
[7] E. A. Carter, “Orbital-free density functional theory dynamics: evolution of thou-
sands of atoms with quantum forces,” in Advances in Compuational Engineering
and Sciences, edited by S. N. Atluri and F. W. Brust, pp. 1967–1968, (Tech Science
Press, Palmdale, 2000).
[8] C. Cercignani, The Boltzmann Equation and its Applications, Springer-Verlag,
Berlin, 1988.
[9] D. Chandler Introduction to Modern Statistical Mechanics, Oxford University Press,
1987.
209
210 BIBLIOGRAPHY
[10] S. Chapman and T. G. Cowling, The Mathematical Theory of Non-uniform Gases:
An Account of the Kinetic Theory of Viscosity, Thermal Conduction, and Diffusion
in Gases, Cambridge University Press, 1939.
[11] M. S. Daw and M. I. Baskes, “Semiempirical, quantum mechanical calculation of
hydrogen embrittlement in metals,” Phys. Rev. Lett., vol. 50, pp. 1285–1288, 1983.
[12] S.R. de Groot and P. Mazur, Non-Equilibrium Thermodynamics, Dover Publications,
1984.
[13] M. Doi and S. F. Edwards, The Theory of Polymer Dyn amics, Oxford Science Pub-
lications, 1986.
[14] W. E and P.-B. Ming, “Cauchy-Born rule and the stability of the crystalline solids:
static problems,” Arch. Rational Mech. Anal., vol. 183, pp. 241–297, 2007.
[15] W. E and P.B. Ming, “Cauchy-Born rule and the stability of the crystalline solids:
dynamic problems,” Acta Math. Appl. Sin. Engl. Ser. vol. 23, pp. 529–550, 2007.
[16] J.L. Ericksen, “On the Cauchy-Born rule”, Mathematics and Mechanics of Solids,
vol. 13: 199220, 2008
[17] J. H. Ferziger and H. G. Kaper, Mathematical Theory of Transport in Gases, North-
Holland Publishing Company, Amsterdam, 1972.
[18] D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to
Applications, 2nd ed., Academic Press, 2001.
[19] N. Goldenfeld, Lectures on Phase Transitions and the Renormalization Group,
Perseus Books, Reading, Mass., 1992.
[20] H. Grad, “On t he kinetic theory of rarefied gases,” Comm. Pure Appl. Math. vol. 2,
pp. 331–407, 1949.
[21] P. Hohenberg and W. Kohn, “Inhomogeneous electron gas,” Phys. Rev., vol. 136,
pp. B864–B871, 1964,
[22] J. H. Irving and J. G. Kirkwood, “The statistical mechanical theory of transport
processes IV,” J. Chem. Phys., vol. 18, pp. 817–829, 1950.
BIBLIOGRAPHY 211
[23] R. D. James, Unpublished lecture notes.
[24] E. Kaxiras, Atomic and Electronic Stucture of Solids, Cambridge University Press,
2003.
[25] C. Kipnis and C. Landim, Scaling Limits of Interacting Particle Systems, Springer,
1999.
[26] W. Kohn and L. Sham, “Self-consistent equations including exchange and correlation
effects,” Phys. Rev., vol. 140, pp. A1133–A1138, 1965.
[27] L. Landau and E. M. Lifshitz, Theory of Elasticity, 3rd ed., Pergamon Press, 1986.
[28] C. D. Levermore, “Moment closure hierarchies for kinetic theories,” J. Stat. Phys.
vol. 83, no. 5-6, pp. 1021–1065, 1996.
[29] T. Li and T. Qin, Physics and Partial Differential Equations, (in Chinese), The High
Eduation Press, Beijing (in Chinese), 2000.
[30] X. Li and W. E, “Multiscale modeling of the d ynamics of solids at finite tempera-
ture,” submitted to J. Mech. Phys. Solids, vol. 53, pp. 1650–1685, 2005.
[31] E. H. Lieb and B. Simon, “The Hartree-Fock theory for Coulomb systems,” Com-
mun. Math. Phys., vol. 53, pp. 185–194, 1977.
[32] M. Marder, Condensed Matter Physics, Wiley-Interscience, 2000.
[33] R. M. Martin, Electronic Structure: Basic Theory and Practical Methods, Cambridge
University Press, 2004.
[34] R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford
University Press, 1989.
[35] D. G. Pettifor, Bonding and Structure of Molecules and Solids, New York, Clarendon
Press, 1995.
[36] L. E. Reichl, A Modern Course in Statistical Physics, University of Texas Press,
Austin, TX, 1980.
[37] H. Spohn, Large Scale Dynamics of Interacting Particles, Springer, Berlin, 1991.
212 BIBLIOGRAPHY
[38] H. Struchtrup, Macroscopic Transport Equations for Rarefied Gas Flows, Springer,
Berlin, New York, 2005.
[39] S. Tsien, Introduction to Physical Mechanics, (in Chinese), Science Press, 1962.
[40] G. A. Voth (eds), Coarse-graining of condensed phase and biomolecular systems,
CRC Press, 2009.
[41] M. Zhou, “A new look at the atomic level virial stress: on continuum-molecular
system equivalence,” Proc. R. Soc. Lond. A, vol. 459, pp. 2347–2392, 2003.
Chapter 5
Examples of Multi-physics Models
The next several chapters will be devoted to numerical algorithms for multiscale
problems. However, before launching into a discussion about numerics, we would like
to make the point that developing better physical m odels based on multiscale, multi-
physics considerations is as least as important, if not more. After all, the ultimate goal
of modeling is to get a better understanding of the physical problem and obtaining better
models is a very important way of getting better understanding. In addition, there is a
very close relation between multiscale algorithms and multiscale models.
Speaking in broad terms, there has been a long history of multiscale, multi-physics
models. One class of such models is associated with the resolution of singularities (shocks,
interfaces and vortices) by introducing additional regularizing terms that often represent
more detailed physics. In Ginzburg-Landau theory, for example, we add gradient terms
to the Landau expansion of the free energy to account for the contribution due to the
spatial variation of the order parameter. This allows us to resolve the internal structure
of the interface between different phases or the internal structure of the vortices, both
are at the micro-scale. Adding viscous and heat conduction terms to equations of gas
dynamics has a similar effect, namely, it allows us to resolve the internal structure of the
shocks.
Another class of examples are those that explicitly involve the coupling of models
at different levels of physics. Car-Parrinello molecular dynamics or first-principle-based
molecular dynamics is one such example (see the next chapter). Other examples include
coupled Brownian dynamics and hydrodynamics models for p olymer fluids, coupled atom-
istic and continuum models for solids, etc.
213
214 CHAPTER 5. EXAMPLES OF MULTI-PHYSICS MODELS
We will discuss three examples in this chapter. In the first example, we describe how
one may use kinetic theory, or Brownian dynamics to supply the constitutive relation
for the stress in polymer fluids. The final result is a coupled Brownian dynamics - hy-
drodynamics model. In the second example, we describe how one may derive continuum
nonlinear elasticity models for nano-structures using atomistic models. The last exam-
ple is the moving contact line problem where better boundary conditions are needed at
the contact line in order to resolve the singularity that arises in the classical continuum
theory.
When water is poured in or drained out of a cup, the th ree different phases, the
air, th e water and the cup, intersect at a line called the contact line. The dynamics of
the contact line is often regarded as being one of the few remaining unsolved problems
in classical fluid dynamics. It is well-known that if we use the classical Navier-Stokes
equation with no-slip boundary condition to describe the problem, we obtain a singularity
at the moving contact line with an infinite rate of energy dissipation [21]. Even though
this singularity is unavoidable at the macroscopic scale, many proposals have been made
to remove this singularity at smaller scales, by changing either the governing PDE or the
boundary condition. While these proposals do succeed in removing the singularity, it is
far from being clear whether they reflect the actual physics going on near the contact
line. One can also use molecular dynamics, or coupled atomistic-continuum models such
as the oned discussed in Chapter 7. These approaches are very useful for discovering new
microscopic physical phenomena, such as the existence of the slip region, but th ey are
inconvenient as analytical tools. We will describe an approach that has been advocated
in [35] in which thermodynamic considerations are used to suggest the form of the right
continuum model, e.g. the form of the boundary condition, and microscopic simulations
are then used to measure the detailed functional dependence of the constitutive relations.
This kind of multiscale modeling should be useful for many other problems of this type,
such as crack propagation, triple junction dynamics, etc.

5.1. BROWNIAN DYNAMICS MODELS OF POLYMER FLUIDS 215
5.1 Brownian dynamics models of polymer fluids
As we have seen before, the hydyrodynamic equations for incompressible fluids can
always be written in the form:
ρ
0
(∂
t
u + (u · ∇)u) + ∇p = ∇ · τ,
∇ · u = 0,
(5.1.1)
where u is the velocity field, p is the pressure, and τ is the viscous stress. Consider
polymers in a solvent. Then τ can be written as τ = τ
s
+ τ
p
where τ
s
is the stress due
to the solvent, τ
p
is the p olymer contribution to the stress. In general we can model τ
s
by a simple linear constitutive relation τ
s
= η
s
D, D = 1/2(∇u + ∇u
T
), where η
s
is the
viscosity of the solvent. The difficulty is in the modeling of τ
p
.
The traditional approach is to model τ
p
via some empirical constitutive relations
[4]. These constitutive relations are extensions of the constitutive relation for Newtonian
fluids discussed in the previous chapter. Examples of such empirical constitutive relations
include:
1. Generalized Newtonian models:
τ
p
= η(D)D (5.1.2)
i.e. th e viscosity coefficient may depend on the strain rate.
2. Maxwell models (for visco-elastic fluids):
τ
p
(x, t) =
Z
t
−∞
η
s
λ
exp
−
t − s
λ
D(x, s)ds, (5.1.3)
where η
s
/λ exp(−(t − s)/λ) is the relaxation modulus representing the memory
effect in the visco-elastic fluid.
3. Oldroyd models:
λ
∇
τ
p
+τ
p
+ f(τ
p
, D) = ηD, (5.1.4)
where
∇
τ
p
=
∂τ
p
∂t
+ (u · ∇)τ
p
− ∇u ·τ
p
− τ
p
· (∇u)
T
(5.1.5)
is the upp er convective derivative [4], λ is a relaxation time parameter. Well-known
examples include the Oldroyd-B model for which f(τ
p
, D) = 0, and the Johnson-
Segalman model for which f(τ
p
, D) = αλ(τ
p
· D + D · τ
p
).
216 CHAPTER 5. EXAMPLES OF MULTI-PHYSICS MODELS
The other extreme is of course the full atomistic model. This is possible but at the
present time, it is not very productive if one wants to study rheological behavior. A more
efficient approach is to coarse-grain the atomistic model, for example, by putting atoms
into groups to form beads. Typical coarse-grained models include:
1. beads and spring models;
2. dumbbell models;
3. rigid-rod models.
Such coarse-grained models have been very useful [3, 42].
In general, the inertial force for the polymer is much smaller than the friction force
against the solvent. Therefore, it is a common practice to neglect the inertial effects and
consider the so-called Brownian dynamics models.
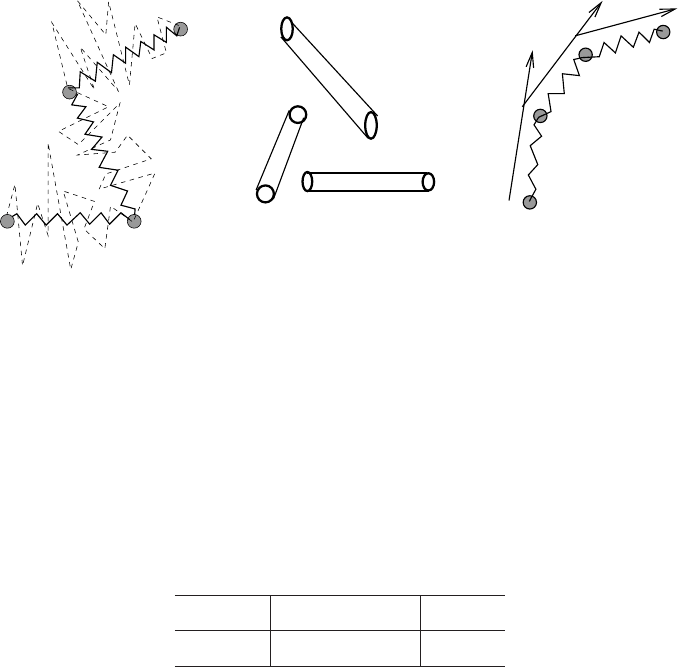
Flexible
Rigid
Semiflexible
Random flight
Additional angle potential
Figure 5.1: Illustration of flexible, semi-flexible and rigid polymers (courtesy of Tiejun
Li).
There are two important length scales in these systems. One is the bending persistence
length of a polymer l
p
, which is defined to be the correlation length for the tangent
vectors at different positions along the polymer. The other is the length of the polymer,
l. According to the relative size of l and l
p
, polymers are classified as
flexible semi-flexible rigid
l ≫ l
p
l ∼ O(l
p
) l ≪ l
p
