Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

487

0.5 1 1.5 2 2.5 3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

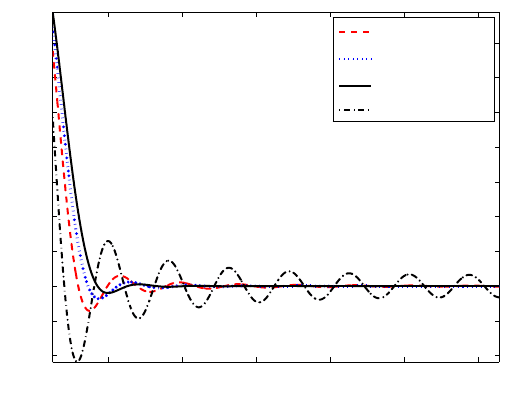
localized basis ψ(x)

weight x

Dirichlet kernel

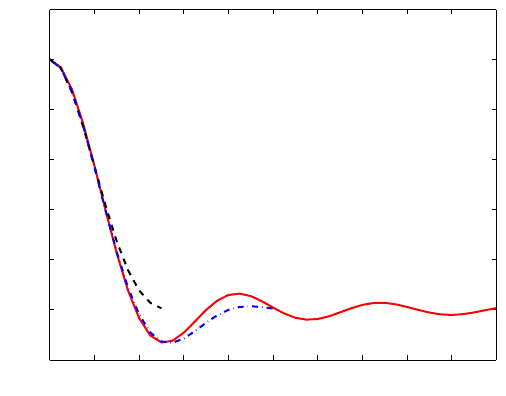
Figure 11.1: The localized bases produced by the weight functions x

(red dashed curve),

(blue dotted curve) and x

(black solid curve) and the Dirichlet kernel with n = 16

(black dot-dashed curve). Here the best localization is obtained with the weight function

488 CHAPTER 11. SOME PERSPECTIVES

eigenvalues and eigenvectors of a matrix. Subspace iteration consists of two main steps:

Multiplication of a set of approximate basis vectors by t he matrix A, followed by orthog-

onalization [14, 21]. The cost of this algorithm is at least O(NM

). [10] proposed a

localized version of the subspace iteration algorithm, the localized subspace iteration or

LSI, in which the orthogonalization step is replaced by a localization step. The resulting

algorithm has a complexity of O(N).

Consider for example the operator

A = −∇ · (a

(x)∇) (11.0.9)

When a

has the form a

(x) = a(x/ε), one can apply the homogenization theory to

reduce the complexity of this operator. In the most general case, one can ask: Given

an integer M, what is the M × M matrix that best approximates this operator? LSI

can be used to ﬁnd this matrix and the associated eigen-subspaces of A. See [10] for

details. In the case when a

has scale separation, the generalized ﬁnite element method,

residual-free bubble element and MsFEM can all be regarded as other ways of ﬁnding

approximately this optimal subspace (see Chapter 8).

Another example, the optimal reduction of Markov chains, has been discussed in [11].

In many cases, this kind of poorman’s optimal prediction procedure can produce

very poor results. For example, CGMD discussed in section 9.3 can be regarded as a

variational model reduction technique applied to molecular dynamics. As indicated there,

the results of CGMD can be qualitatively incorrect, since it neglects entirely the memory

eﬀect.

11.0.2 Modeling memory eﬀects

From a theoretical viewpoint, one can always eliminate degrees and obtain a “reduced

system” using the Mori-Zwanzig procedure, as was explained in Section 2.7. Here we put

“reduced system” in quotation marks since the complexity of the models obtained from

the Mori-Zwanzig procedure is not necessarily reduced: It contains the same amount of

information as the orginal model, except that the initial data for the eliminated degrees

of freedom is replaced by a random process. The complexity coming from the extra

degrees of freedom in the original model is replaced by the complexity from the memory

kernels in the Mori-Zwanzig formalism. Therefore unless we make approximations for

the memory kernels, these “reduced models” may just be as complicated as th e models

489

we begin with. This does not mean that the Mori-Zwanzig formalism is useless. In fact,

it provides a natural starting point for making approximations to the memory kernels.

From the viewpoint of the Mori-Zwanzig formalism, when the time scales for the

eliminated degrees of freedom are much shorter than the time scales for the variables

retained, the memory terms are very small and can be neglected. We have already seen

many examples of this kind.

In the other extreme when the memory kernels are long-ranged and slowly varying,

one can make a diﬀerent kind of approximation, as was done in [6, 16] to obtain the

t-model.

In between these two extreme cases we ﬁnd the most diﬃcult situation. Consider the

simplest example of this kind – a one-dimensional chain of atoms with nearest neighbor

interaction [1]

m¨x

= φ

′

j+1

− x

) − φ

′

− x

j−1

), −∞ < j < ∞ (11.0.10)

say with the Lennard-Jones potential:

φ(r) = 4ε



(σ/r)

− (σ/r)



(11.0.11)

The lattice parameter for this system is a

√

2 σ, and the displacement is deﬁned as

= x

− ja

. The p honon dispersion relation for this system is given by:

ω(k)



2 − 2 cos (ka

)



, k ∈



−



(11.0.12)

where κ

= φ

′′

We split the chain of atoms into two groups, one group consists of atoms whose

dynamics is what we are interested in and another consists of atoms that play the role of

heat bath. We deﬁne the heat bath as the set of atoms with j 6 0. After adopting the

harmonic approximation for the heat bath atoms, we obtain the following Hamiltonian

for the whole system:

H =

j60



j+1

− u



j>0

φ(x

j+1

− x

) +

Here v

is the velocity for the j-th atom. If we apply the Mori-Zwanzig formalism to

eliminate the heat bath atoms, we obtain the generalized Langevin equation (GLE) for

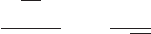
490 CHAPTER 11. SOME PERSPECTIVES

the retained atoms (see [1]):

m¨u

= φ

′

− x

) −

θ(t − s) ˙u

(s)ds + F (t),

m¨u

= φ

′

j+1

− x

) − φ

′

− x

j−1

), j > 1 (11.0.13)

where

θ(t) =

√

m κ



2κt

√



, (11.0.14)

F (t) =

j60

(t)



j+1

(0) − u

(0)



+ s

(t)v

(0).

Here J

is a Bessel function of the ﬁrst kind. The coeﬃcients c

(t) and s

(t) are governed

˙s

= c

j−1

− c

m ˙c

= κ

− s

j+1

(t) = 0, s

(0) = 0, c

−1

(0) = −κ

, c

(0) = 0, j ≤ −2

The term F (·) is often treated as a noise term. More examples of th is kind of analysis

can be found in [17].

The GLE is still quite complicated due to the presence of the long range kernels. For

high dimensional models, these long range kernels also have a spatial component that

couple all the boundary atoms together. Modeling such memory-dependent dynamics is

still a highly demanding task. Therefore it is desirable to make approximations [9]. A

systematic approach for making such approximations has been proposed in [18], based

on the following principles:

1. Eﬃciency: The kernels should be as local as possible.

2. Accuracy: Given the size of the time interval and the set of neighboring atoms that

the kernels depend on, we are interested in ﬁnding the most accurate approximation

to the original dynamics.

3. Stability: The approximate GLEs should be stable. This will constrain the approx-

imate kernels to be positive deﬁnite.

4. The noise term should be app roximated accordingly. For example, when applicable,

the ﬂuctuation-dissipation theorem should be preserved.

491

One interesting observation made in [18] is that one can “use space to buy time”,

i.e. by increasing the set of neighboring atoms that the memory kernels depend on, one

can increase the rate of decay of the memory kernels. For this reason, it is of interest to

increase the spatial dependence of the memory kernels since this is often more convenient

than dealing with long range memory terms. More details can be found in [9] and [18].

The work in [9, 18] is an interesting st art, but it is limited to the situation when

the interaction involving the eliminated degrees of freedom is approximately linear. The

problem is basically open for the more general cases.

492 CHAPTER 11. SOME PERSPECTIVES

0 5 10 15 20

−0.2

0.2

0.4

0.6

0.8

14 16 18

−0.05

0.05

10.6 10.8 11

0.8

0.85

0.9

0.95

Figure 11.2: The homogenization problem: The localized bases produced by the weight

functions x

(blue solid curve), x

(black solid curve), 1 −χ

[−1,1]

(red dashed curve) and

1−χ

[−2,2]

(magenta dot-dashed curve). The b ottom inset shows the t ail region; while the

top inset shows the oscillatory behavior of the basis functions in more detail. Courtesy

of Jianfeng Lu.

493

0 5 10 15 20

0.2

0.4

0.6

0.8

12 12.5 13

−0.1

0.1

0.2

0.3

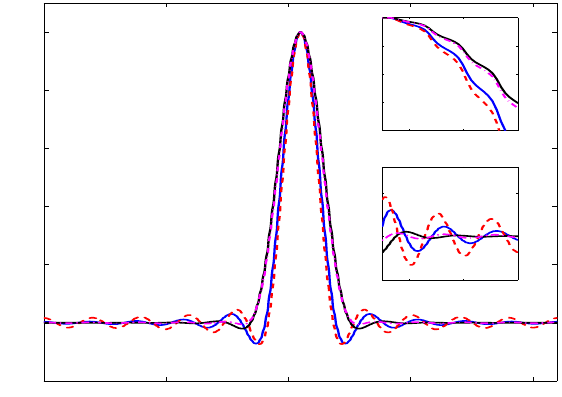
Figure 11.3: The homogenization problem: The localized bases produced by the weight

functions x

(black solid curve) and 1−χ

[−2,2]

(magenta dot-dashed curve) compared with

the basis function of the generalized ﬁnite element method (or MsFEM) with support

size 2 (red dashed curve) and 4 (blue solid curve). The inset shows the detail of these

basis functions two coarse grids away from the center. Courtesy of Jianfeng Lu.

u u

−1 2

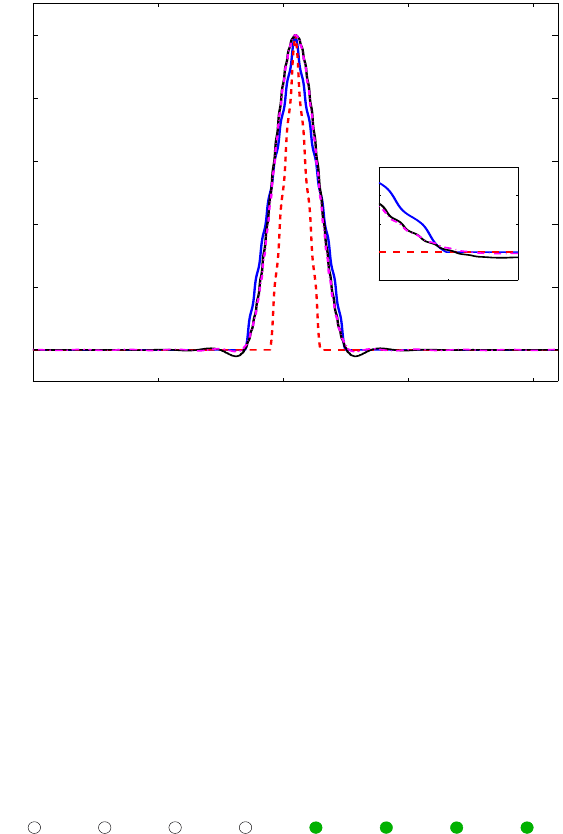
Figure 11.4: An illustration of the eliminated and retained degrees of freedom. The

degrees of freedom associated with the ﬁlled circles are kept. Others are eliminated.

494 CHAPTER 11. SOME PERSPECTIVES

0 1 2 3 4 5 6 7 8 9 10

−0.2

0.2

0.4

0.6

0.8

θ(t)

Figure 11.5: A typical memory kernel (solid line) and local approximations (dashed lines).

Bibliography

[1] S. A. Adelman and J. D. Doll, “Generalized Langevin equation approach for

atom/solid-surface scattering: Collinear atom/harmonic chain model,” J. Chem.

Phys., vol. 61, pp. 4242–4245, 1974.

[2] S. A. Adelman and J. D. Doll. “Generalized Langevin equation approach for

atom/solid-surface scattering: General formulation for classical scattering oﬀ har-

monic solids,” J. Chem. Phys., vol. 64, pp. 2375–2388, 1976.

[3] R.B. Bird, C.F. Curtiss, R.C. Armstrong and O. Hassager, Dynamics of Polymeric

Liquids, Vol. 2: Kinetic Theory, John Wiley, New York, 1987.

[4] A.J. Chorin, O. Hald and R. Kupferman, “Optimal prediction with memory,” Phys-

ica D, vol. 166, no. 3-4, pp. 239–257, 2002.

[5] A.J. Chorin, A.P. Kast and R. Kupferman, “Optimal prediction of u nderr esolved

dynamics,” Proc. N atl. Acad. Sci. USA, vol. 95, no. 8, pp. 4094–4098, 1998.

[6] A.J. Chorin and P. Stinis, “Problem reduction, renormalization, and memory”,

Comm. Appl. Math. Comp. Sc., vol. 1, pp. 1-27, 2005.

[7] S. Curtarolo and G. Ceder, “Dynamics of an inhomogeneously coarse grained mul-

tiscale system,” Phys Rev Lett., vol. 88, pp. 255504–255504-4, 2002.

[8] P. Drineas, R. Kannan, and W. Mahoney, “Fast Monte Carlo algorithms for matrices

II: Computing low-rank approximations to a matrix,” SIAM J. Sci. Comp., vol. 36,

pp. 158–183, 2006.

[9] W. E and Z. Huang, “Matching conditions in atomistic-continuum modeling of ma-

terials,” Phys. Rev. Lett., vol. 87, no. 13, pp. 135501–135501-4, 2001.

495

496 BIBLIOGRAPHY

[10] W. E, T. Li and J. Lu, “Localized basis of eigen-subspaces and operator compres-

sion,” Proc. N atl. Acad. Sci. USA, vol. 107, pp. 1273-1278, 2010.

[11] W. E, T. Li and E. Vanden-Eijnden, “Optimal partition and eﬀective dynamics of

complex networks,” Proc. Natl. Acad. Sci. USA, vol. 105, pp. 7907–7912, 2008.

[12] W. E, T. Li and E. Vanden-Eijnd en, “Variational model reduction,” in preparation.

[13] W. Gao, and W. E, “Orbital minimization with localization,” Discret. Contin. Dyna.

Sys. Ser. A, vol. 23, pp. 249–264, 2009.

[14] G. Golub, and C. Van Loan, Matrix Computation, The Johns Hopkins Univ. Press,

Baltimore, 1996.

[15] D. Gottlieb, and C. W. Shu, “On the Gibbs phenomenon and its resolution,” SIAM

Rev., vol. 39, pp. 644–668, 1997.

[16] O. H. Hald, P. Stinis “Optimal prediction and the rate of decay for solutions of the

Euler equations in two and three dimensions,” Proc. Nat. Acad. Sci. USA, vol. 104,

no. 16, pp. 6527–6553, 2007.

[17] E. G. Karpov, G. J. Wagner and W. K. Liu, “A Green’s function approach to

deriving wave-transmitting boundary conditions in molecular dynamics,” Int. J.

Numer. Meth. Engng., vol. 62, pp. 1250–1262, 2005.

[18] X. Li and W. E, “Variational boundary conditions for molecular dynamics simula-

tions of crystalline solids at ﬁnite temperature: Treatment of the thermal bath,”

Phys. Rev. B, vol. 76, no. 10, pp. 104107–104107-22, 2007.

[19] N. Marzari, and D. Vanderbilt, “Maximally localized generalized Wannier functions

for composite energy bands,” Phys. Rev. B, vol. 56, pp. 12847–12865, 1997.

[20] A.S. Monin and A.M. Yaglom, Statistical Fluid Mechanics, Vol. I: Mechanics of

Turbulence, Dover Publications; Dover Ed edition, 2007.

[21] Y. Saad, Numeri cal Methods for Large Eigenvalue Problems, Manchester Univ.

Press, Manchester, 1992.