Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

10.1. THEORETICAL BACKGROUND 447

Note also that m

(x) is not normalized: In fact, the total integral of m

gives the

probability of being A − B reactive.

2. What is the current associated with these reactive trajectories? The current asso-

ciated with the reactive paths is a vector ﬁeld J

: Ω 7→ R

, Ω = R

\(A ∪ B) such

that the following holds:

lim

T →∞

[−T,T ]

x(t)δ(x − x(t))1{t ∈ R}dt = J

(x) (10.1.69)

Note that if we consider the whole trajectory x(·) (not just t he reactive pieces),

then we have

lim

T →∞

[−T,T ]

x(t)δ(x − x(t))dt = J(x) (10.1.70)

where J(x) = (J

(x), . . . , J

(x))

∈ R

is the “equilibrium current” (or more

precisely the steady state current) with

(x) = b

(x)m(x) −

j=1

∂

∂x

(x)m(x)) (10.1.71)

This is obtained from the forward Kolmogorov equation, which can be written as

∂

ρ(x, t) + ∇ · (b(x)ρ(x, t) − ∇(a(x)ρ(x, t))) = 0 (10.1.72)

J is divergence-free. But it does not necessarily vanish for non-gradient systems,

since the detailed balance condition may not hold.

3. Transition rate: If N

is the number of A − B reactive trajectories of the given

trajectory x(·) in [−T, T ], what is the limit of N

/(2T ) as T → ∞?

= lim

T →∞

(10.1.73)

To answer these questions, we need the notion of committor functions [15], also re-

ferred to as the capacitance functions in the mathematics literature.

Let q

: Ω 7→ [0, 1] be the solution of

:= b ·∇q

+ a : ∇∇q

= 0, q

∂A

= 0, q

∂B

= 1 (10.1.74)

448 CHAPTER 10. RARE EVENTS

is called the forward committor function for the transition process from A to B. In

a similar fashion, we can deﬁne the backward committor function q

−

: Ω 7→ [0, 1] as the

solution of

−

:= −b·∇q

−

div(am)·∇q

−

+a : ∇∇q

−

= 0, q

−

∂A

= 1, q

−

∂B

= 0 (10.1.75)

and q

−

have a very simple interpretation: q

(x) is the probability that a trajectory

initiated at x will reach B before it hits A, q

−

(x) is the probability that a trajectory

arriving at x came from A, i.e. it did not hit B in between. The level sets of these

functions are called the isocommittor surfaces [15]. The level set {q

= 1/2} is of

particular interest: Points on this surface have an equal probability of ﬁrst reaching A

and B. This is the dividing surface t hat separates the reactant states from the product

states.

For gradient systems

x = −∇V (x) +

√

w (10.1.76)

we have q

= 1 − q

−

and q

satisﬁes the equation:

∆q

− ∇V · ∇q

= 0 (10.1.77)

Consider the simple example of a two-dimensional gradient system with potential

V (x

, x

) =

(1 − x

)

+ 5x

(10.1.78)

and let us take A = {x

< −0.8}, B = {x

> 0.8}. It is easy to see that in this case the

solution of (10.1.77) is only a function of x

: q

, x

) = 1 − q

−

, x

) ≡ q(x

) where

q(x

) =

−0.8

(1−z

)

0.8

−0.8

(1−z

)

(10.1.79)

The questions raised above can all be answered in terms of the quantities just deﬁned.

We will simply summarize the results. Details of the calculation can be found in [23].

1. Probability density of reactive trajectories.

We have m

(x) = q

(x)q

−

(x)m(x)

lim

T →∞

[−T,T ]∩R

φ(x(t))1{t ∈ R}dt =

Ω

(x)q

−

(x)m(x)φ(x)dx (10.1.80)

10.1. THEORETICAL BACKGROUND 449

If we limit ourselves to the ensemble of reactive trajectories and ask what the probability

density of ﬁnding them at x is, we have

ˆm

(x) =

(x)q

−

(x)m(x) (10.1.81)

where the normalization factor

Ω

(x)q

−

(x)m(x)dx (10.1.82)

is the probability to be reactive.

As an illustration, consider the simple example of the gradient system discussed above.

Shown in Figure 10.1.5 are the equilibrium probability density m and the probability

density for the A −B reactive trajectories m

. Notice that m peaks at the local minima,

whereas m

peaks at the saddle point, due to the fact that the reactive trajectories are

slowed down at the saddle point (hence it has to spend more time there) where the drift

term vanishes in the stochastic dynamics.

2. The current of A − B reactive trajectories.

This is given by

= q

−

J + mq

−

a∇q

− mq

a∇q

−

(10.1.83)

where J was given in (10.1.71). Note that div J

= 0 in Ω. Note also that

∂A

(x) · J

(x) = m(x)

i,j=1

∂A,i

(x)a

(x)

∂q

(x)

∂x

= m(x)|∇q

(x)|

−1

i,j=1

(x)

∂q

(x)

∂x

∂q

(x)

∂x

≥ 0.

(10.1.84)

where

∂A

(x) is the unit outward normal of ∂A which can also be deﬁned as ∇q

/|∇q

Similarly, one can show that

∂B

(x) · J

(x) ≤ 0 (10.1.85)

where

∂B

is the unit outward normal of ∂B.

3. The transition rate.

Let S be a dividi ng surface, i.e. a hypersurface in Ω that separates A and B, then

= lim

T →∞

(x) · J

(x)dS (10.1.86)

450 CHAPTER 10. RARE EVENTS

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

2.2

−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

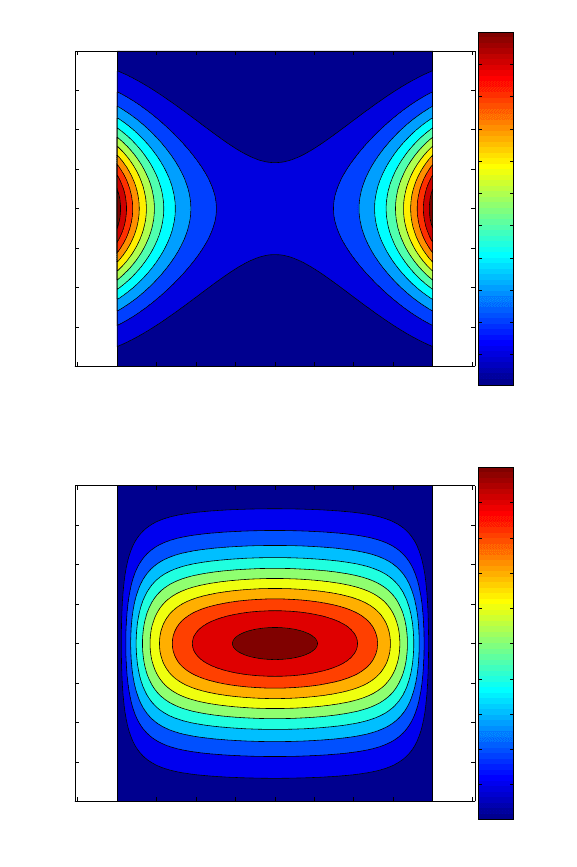
Figure 10.4: Equilibrium density and density of reactive trajectories for the example

(10.1.78), from [23]. The top ﬁgure shows the equilibrium density for the whole system.

The bottom ﬁgure shows the equilibrium density for the reactive trajectories. It is clear

that the equilibrium density for the whole system concentrates on the wells whereas the

equilibrium density for the reactive trajectories concentrates at the saddle point.

10.1. THEORETICAL BACKGROUND 451

Since J

is divergence-free, div J

= 0, it is easy to see that the integral over S deﬁned

above is actually independent of S. In fact, one can show that [23]

Ω

ha∇q

, ∇q

im(x)dx =

Ω

j,k

(x)∂

(x)m(x)dx (10.1.87)

For the setting considered in (10.0.3), we have

(x) = Z

−1

−V (x)/ε

∇q

(x) (10.1.88)

where Z

Ω

−V (x)/ε

dx. The t ransition rate is given by:

Ω\(A∪B)

−V (x)/ε

|∇q

(x)|

dx (10.1.89)

In fact, it is easy to see that the transition rate admits a variational formulation: Deﬁne

I(q) =

Ω

−V (x)/ε

|∇q(x)|

dx (10.1.90)

then

min

I(q) (10.1.91)

subject to the boundary condition that q = 0, 1 at ∂A and ∂B respectively.

4. Streamlines of the reactive current.

Given the vector ﬁeld J

, we can deﬁne the dynamics:

dx(τ)

dτ

= J

(x(τ)) (10.1.92)

where τ is an artiﬁcial time parameter, which should n ot be confused with the physical

time of the original trajectory x(·). Solutions to this equation deﬁne the streamlines for

the reactive current J

. They are u seful for deﬁn ing the transition tube.

5. The transition tube.

So far our statements are exact. Next we will deﬁne the analogous object of the

minimum energy path (or the most probable paths) for complex systems. For this to

make any sense, the system must be such that the reactive trajectories are localized in

the conﬁguration or phase space. This is not the case, for example, when the barrier is

mainly entropic in nature (an example is discussed below). Here we will limit ourselves

452 CHAPTER 10. RARE EVENTS

to the situation when the reactive trajectories are indeed localized, in the sense to be

made more precise below.

Suppose that we identify a (localized) region on ∂A, say S

⊂ ∂A, which contains a

(1 − δ) portion of the reactive current that goes out of A

∂A

(x) · J

(x)dS = (1 − δ)

∂A

(x) · J

(x)dS = (1 − δ)ν

(10.1.93)

Let S(τ) be the image of S

under the ﬂow map deﬁned by (10.1.92) at (the artiﬁcial)

time τ. Using the divergence theorem, we have

∂A

(x) · J

(x)dS =

S(τ )

(x) · J

(x)dS. (10.1.94)

We deﬁne the union of the S(τ)’s as the transi tion tube that carries 1 − δ portion of the

probability ﬂux of reactive trajectories.

When discussing the transition tube, we have implicitly made the localization as-

sumption, i.e. the diameter of the sets S(τ) is much smaller than the radius of curvature

of the centerline curve of t he tube. As was shown in [22], it is possible to establish an

approximate characterization of the transition tube using the ratio of the tube width and

the radius of curvature of the centerline as the small parameter to develop the asymp-

totics. Given a curve γ that connects A and B, let z be an arbitrary point along γ, let P

be the hyperplane normal to γ and den ote by µ

(dS) the restriction of the equilibrium

distribution µ(dx) to P

. It was shown in [22] that under the localization assumption,

the centerline of the transition tube γ

⋆

is approximately a principal curve with respect to

the family of distributions {µ

}: For every point z along the centerline γ

⋆

, if C(z) is the

center of mass of the distribution µ

on P

, then C(z) coincides with z, upto an error of

size ε:

C(z) = hxi

= z + O(ε) (10.1.95)

This characterization is the basis for the ﬁnite temperature string method, to be discussed

in the next section. Once the centerline curve is found, one can determine the width of

the transition tube by identifying the standard deviation of the distribution µ

on P

In the zero temperature limit, C(z) becomes a local minimizer of V restricted to P

Therefore the principal curve becomes the MEP.

The emp loyment of the hyperplanes is not necessary in this characterization. Other

objects, such as the iso-committor surfaces or the sets {S(τ)}, can also be used.

10.1. THEORETICAL BACKGROUND 453

−0.5 0 0.5

−0.5

0.5

x 10

−6

−0.5 0 0.5

−0.5

0.5

0.2

0.4

0.6

0.8

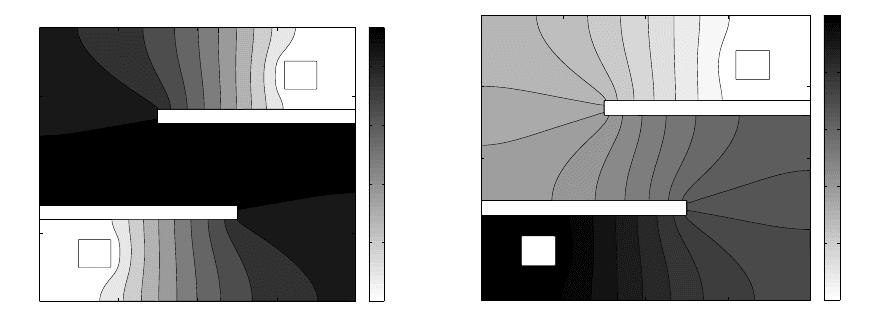
Figure 10.5: Probability density of reactive trajectories (upper) and the the committor

function (lower panel) for the example with an entropic barrier. From [43].

One may ask: How realistic is the localization assumption? Well, if it is violated,

it means that the transition paths are very diﬀusive. This is the case when entropic

barriers are dominant. To characterize the transition path ensemble in this situation,

one has to ﬁnd some coarse-grained variables to represent the entropic factors. At the

present time, there is no systematic way of doing this. Nevertheless, it should be noted

that transition path theory is equally valid in this case, even though the localization

assumption is violated.

6. Transition state ensemble. In the TPT language, the transition state ensemble

is simply the distribution µ

(dx) = m

(x)dx. For simple systems, this distribution is

sharply peaked at the transition states, the saddle points of the energy. Therefore, one

may replace the notion of the transition state ensemble by that of the transition state.

For complex systems, this is not necessarily the case. In fact, when entropic barrier

dominates, the transition state ensemble can be a rather ﬂat distribution, as we will

see later. When energy barrier dominates, the transition state ensemble should still be

454 CHAPTER 10. RARE EVENTS

−0.5 0 0.5

−0.5

0.5

Figure 10.6: A typical reactive trajectory for the example with an entropic barrier. From

[43].

peaked. The region that contains most of the masses of µ

is the bottleneck for the

transition, and should be considered as the analog of the transition states in TST.

7. Reaction coordinates. The notion of reaction coordinates has been used widely,

often incorrectly. Reaction co ordinates are variables that fully characterize the progress of

the reaction. There is an obvious reaction coordinate, namely the committor function q

The family of iso-committor surfaces give a geometric characterization of the progress of

the reaction. Given a set of functions r = (r

, r

, ··· , r

) where r

= r

(x), r can be used

as reaction coordinates if and only if it distinguishes the diﬀerent iso-committor surfaces,

i.e. for any two points x

and x

in Ω, r(x

) = r(x

) implies that q

) = q

We should distinguish the notion of reaction coordinates with that of the slow vari-

ables. The following example illustrates this point (see also [24]). Consider a two-

dimensional conﬁguration space with the energy function

V (x, y) =

(1 − x

)

(10.1.96)

where as usual ε ≪ 1. This is a bi-stable system with local minima (−1, 0) and (1, 0).

The slow variable in this problem is y, but the reaction coordinate for the transition

between the two local minima is x.

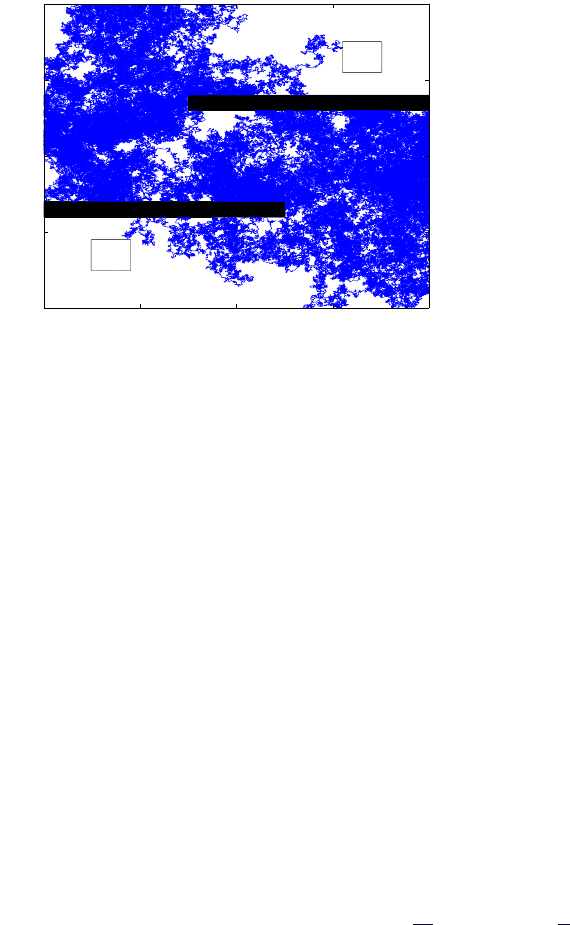
An example with entropic barrier [43]. Consider diﬀusion in the S-shaped re-

gion shown in Figure 10.5. We deﬁne the sets A and B to be the little squares at the

upper-right and bottom-left corners respectively. In this example, there are no potential

10.2. NUMERICAL ALGORITHMS 455

barriers, in fact, V = 0. However, there is an entropic barrier: Transition paths have to

ﬁnd their way between the two obstacles. Sup pose we start the dynamics in A. The closer

the trajectory gets to the region enclosed by the obstacles the higher the probability that

the trajectory will ﬁnally reach the lower-left corner before returning to A because the

probability to end up in B depends roughly on the distance between the current position

and the set B. Figure 10.5 shows the probability density for the reactive trajectories

and the committor function q(x, y) for this example. In Figure 10.6 we depict a typical

reactive trajectory. One can see that the trajectory spends most of its time between

the obstacles. This is consistent with the behavior of the probability density function

of reactive trajectories. Although not shown here, the probability current of reactive

trajectories is as expected: Basically, the streamlines follow the S-shape (see [43]).

10.2 Numerical algorithms

In this section, we will discuss numerical algorithms that have been developed for

computing the transition states, minimum energy paths and transition tubes. We will

restrict our attention to gradient systems.

10.2.1 Finding transition states

In the simplest case when the energy landscape is smooth, the most important objects

for the transition between the locally stable states are the transition states, which are

the saddle points separating the stable states. These saddle points are special critical

points for the potential V . They satisfy the equation:

∇V (x) = 0 (10.2.1)

If we have a rather good guess about the location of the particular saddle point, we

can use Newton’s method to solve (10.2.1) and ﬁnd the relevant saddle point. This is

quite eﬃcient but requires knowing a very good initial guess.

A more general approach is the dimer m ethod [33]. This is an iterative procedure

that involves a dimer, which consists of two images of the system connected by a short

line segment, say of length δ. The energy of the dimer is the sum of the energies of the

two images. The dynamics of the dimer is determined by the translation of t he mid-point

456 CHAPTER 10. RARE EVENTS

of the line segment and the rotation of the line segment. Each iteration consists of two

steps:

1. Rotating the dimer. The best orientation of the dimer is found by minimizing the

energy of the dimer with the mid-point ﬁxed. This can be done using, for example,

Newton’s method. The energy diﬀerence for the diﬀerent orientations of the dimer

is related to the curvature in diﬀerent directions. The minimum energy orientation

is given by the lowest curvature direction.

2. Translating the dimer. First we deﬁne the force on the dimer: F = (F

+ F

)/2,

where F

and F

are the forces acting on the ﬁrst and second images respectively. If

we use this force to move the dimer, the dimer will end up near the local minimum

state for the potential. In order to reach the saddle point, one idea is to reverse

the force in the direction of the dimer, i.e. let

∗

= F − 2F

(10.2.2)

where F

is the component of F in the direction of the dimer. The dimer is then

parallelly translated by moving its mid-point by ∆tF

∗

where ∆t is some appropriate

time step size.

The dimer method is fairly eﬀective, but it is not fo ol-proof either. There is no

guarantee that it will reach the relevant saddle point for the transition we are interested

in, since no information about the ﬁnal state of the transition is used.

Besides the two discussed above, there are many other methods (see for example,

[35]) for computing saddle points. The nudged elastic band method discussed below,

particularly the climbing image nudged elastic band method (CI-NEB), is also targeted

toward computing saddle points.

10.2.2 Finding the minimal energy path

If the stable states we are interested in are separated by multiple saddle points and

intermediate stable states, then it becomes quite diﬃcult to use direct saddle point

searching methods to ﬁnd the sequence of relevant saddle points. In this case, we really

should look for the minimum energy path (MEP).