Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

9.2. APPLICATION OF HMM TO STOCHASTIC SIMULATION ALGORITHMS407

However, unlike standard examples of HMM, here we do not need to know what the

slow and fast variables are, in order to carry out the computation. The algorithm is

formulated in terms of the original variables. This is to be expected, since the eﬀective

dynamics can also be formulated in terms of the original variables (see section 2.3.3).

Convergence and eﬃciency of the nested SSA

The original SSA is an exact realization of the stochastic chemical kinetic system.

The nested SSA, on the other hand, is an approximation. The errors in the nested SSA

can be analyzed using the general strategy for analyzing HMM (see section 6.7). The

details can be found in [13].

Assume as in section 2.3.3 that there is a complete set of slow variables of the form

= b

· x, j = 1, ··· , J}, where {b

, j = 1, ··· , J} is a set of basis vectors in the

subspace of vectors that are orthogonal to all the vectors {ν

}. Let f be a smo oth

function. Denote by

the solution of the n ested SSA. Consider the observable v(x, t) =

f(b ·

) where the expectation is taken with respect to the randomness in the outer

SSA only. Let u(x, t) be the solution of the eﬀective equation (2.3.82) with u(x, 0) =

f(b · x). The following result is proved in [12, 13]:

Theorem. For any T > 0, there exist constants C and α indepen dent of (N, T

, T

) such

that,

sup

0≤t≤T,x∈X

E |v(x, t) − u(x, t)| ≤ C

ε +

−αT

/ε

1 + T

/ε

N(1 + T

/ε)

. (9.2.6)

This result can be used to analyze the eﬃciency of the nested SSA. Given a chemical

kinetic system with R = {(a

, ν

)}, we assume that the total rate a(x) =

(x) does

not ﬂuctuate a lot in time: a(x) ∼ O(ε

−1

). Given an error tolerance λ, we choose the

parameters in the nested SSA such that each term in (9.2.6) is less than O(λ). One

possible choice of the parameters is

= 0, N = 1 + ε

−1

. (9.2.7)

The total cost for the nested SSA over a time interval of O(1) is

Cost = O(N(1 + T

/ε + T

/ε)) = O





. (9.2.8)

In comparison, the cost for the direct SSA is

Cost = O





. (9.2.9)

408 CHAPTER 9. PROBLEMS WITH MULTIPLE TIME SCALES

since the time step size is of order ε. When ε ≪ λ

, the nested SSA is much more eﬃcient

than the direct SSA.

Next we discuss the inﬂuence of the other numerical parameters on the eﬃciency. The

parameter T

which plays the role of numerical relaxation time does not inﬂuence much

the eﬃciency. Given the same error tolerance λ, for the last term in the error estimate

(9.2.6) to be less than O(λ), we need to have



1 +



≥ O





. (9.2.10)

Therefore

Cost ≥ O(N



1 +

−1



) = O





. (9.2.11)

which is the same as (9.2.9) regardless the value of T

. The above argument also implies

that the optimal cost for the nested SSA is O





to achieve an error tolerance of λ.

Turning now to the eﬀect of parameter N, the number of realizations for inner SSA,

let us see what happens when we take N = 1. For the error estimate (9.2.6) to satisfy

the same error tolerance λ, we have to choose

1 +

. (9.2.12)

The cost of the nested SSA is given by

Cost = O(N



1 +



) = O





, (9.2.13)

which is the same as the cost if we use multiple realizations. This means that u sing

multiple realizations in the inner SSA does not increase the eﬃciency of the overall

scheme either. Obviously, using multiple realizations is advantageous for implementation

on parallel computers .

Other versions of the nested SSA are discussed in [40, 39]. Although they appear to

be quite diﬀerent, it can b e shown that they are essentially the same as the nested SSA

discuss here.

A numerical example: A virus infection mo del

As a concrete example, we discuss a virus infection model studied in [12, 22]. The

model was originally proposed in [41] as an example of the failure of modeling react-

ing networks with deterministic dynamics. The reactions considered in this model are

9.2. APPLICATION OF HMM TO STOCHASTIC SIMULATION ALGORITHMS409

nucleotides

=1.×template

−−−−−−−−−−−−−−−−−−−−−−→

genome

nucleotides + genome

=.025×genome

−−−−−−−−−−−−−−−−−−−−−−−→

template

nucleotides + aminoacids

=1000×template

−−−−−−−−−−−−−−−−−−−−−−−−→

struct

∗

template

=.25×template

−−−−−−−−−−−−−−−−−−−−−−−→

degraded

struct

=1.9985×struct

−−−−−−−−−−−−−−−−−−−−−−−→

degraded/secreted

∗

genome + struct

=7.5d−6×genome×struct

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−→

virus

Table 9.1: Reaction channels of the virus infection model

listed in Table 9.1 with M

= 6. The species that need to be modeled are genome,

struct, template and virus (N

= 4). Genome is the vehicle of th e viral genetic infor-

mation which can take the form of DNA, positive-strand RNA, negative-strand RNA, or

some other variants. Struct represents the structural proteins that make up the virus.

T emplate refers to the form of the nucleic acid that is transcribed an d involved in catalyt-

ically synthesizing every viral component. The nucleotides and amino acids are assumed

to be available at constant concentrations.

When template > 0, the production and degradation of struct, which are the third

and ﬁfth reactions marked with ∗ in table 9.1, are faster than the others. From the

reaction rates, we can see that the ratio of time scales is about ε = 10

−3

. In a system

that consists of only the fast reactions, struct has an equilibrium distribution which is

Poisson with parameter λ = 500 × template such that

template

(struct = n) =

(500 × template)

exp(−500 × template). (9.2.14)

Notice that struct only shows up in the last slow reaction. The reduced dynamics in

the form of the slow reactions (a

1,2,4,6

) with the rates averaged with respect to the quasi-

equilibrium of the fast reactions (a

3,5

) can be given as a system with 4 reactions, sh own

in table 9.2. The initial condition is chosen to be:

(struct, genome, template, virus) = (0, 0, 10, 0). (9.2.15)

410 CHAPTER 9. PROBLEMS WITH MULTIPLE TIME SCALES

The mean value and the variance of template at time T = 20 are used as benchmark.

A computation of these values by a direct SSA using N

= 10

realizations led to

template = 3.7170 ± 0.005, var(template) = 4.9777 ± 0.005. (9.2.16)

For the nested SSA, we make a series of simulations in which we choose the size of the

ensemble and the simulation time of the inner SSA according to

(N, T

, T/ε) = (1, 0, 2

), (9.2.17)

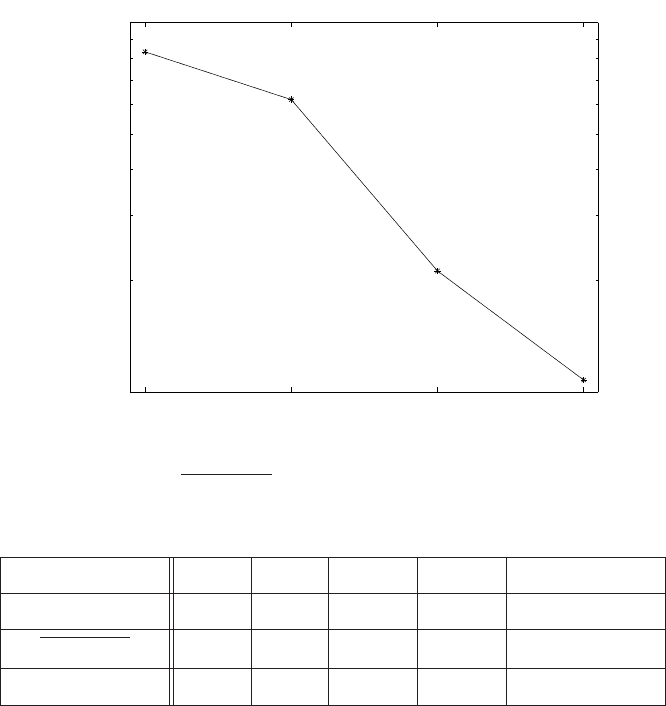
for diﬀerent values of k = 0, 1, 2, 3, . . .. The error estimate in (9.2.6) then implies that

the error δ should decay with the rate:

δ = O(2

−k

). (9.2.18)

which is consistent with the results in Figure 9.3. Table 9.3 gives the total CPU time

and the obtained values of

template and var(template) with the parameters of inner SSA

chosen according to (9.2.17) and using N

= 10

realizations of the outer SSA (same as

in the direct SSA).

9.3 Coarse-grained molecular dynamics

Coarse-grained molecular dynamics (CGMD) is a concept that has been around,

maybe implicitly, for a long time. When we develop bead-spring models of polymer

dynamics, we have in mind not a full atom model, but rather a coarse-grained model,

even though we do not necessarily call it as such. In the last decade or so, this notion

has attracted more attention and has been used quite extensively in several contexts:

nucleotides

=1.×template

−−−−−−−−−−−−−−−−−−−−−−→

genome

nucleotides + genome

=.025×genome

−−−−−−−−−−−−−−−−−−−−−−−→

template

=.25×template

−−−−−−−−−−−−−−−−−−−−−−−→

degraded

genome + struct

=3.75d−3×genome

×struct

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−→

virus

Table 9.2: The reduced virus infection model

9.3. COARSE-GRAINED MOLECULAR DYNAMICS 411

1 2 3 4

−2

−1

Error

Figure 9.3: Relative errors of template using the nested SSA for the virus infection model

(courtesy of Di Liu)

/ε 1 4 16 64 “exact

′′

CP U 154.8 461.3 2068.2 9190.9 34806.4

template 4.027 3.947 3.796 3.757 3.717 ± 0.005

var(template) 5.401 5.254 5.007 4.882 4.978 ± 0.005

Table 9.3: Eﬃciency of the nested SSA for the virus infection model

1. Multiscale simulations in material science, in which CGMD is used as a bridge

between full atomistic simulations and ﬁnite element methods based on continuum

models [37].

2. Coarse-grained models of macromolecules. This is an extension of the bead-spring

type of models for polymers, but with more attention on getting quantitatively cor-

rect eﬀective potential for the coarse-grained model. Techniques such as Boltzmann

inversion has been used to extract such p otentials from long time trajectories of

full MD simulation [46].

3. Free energy exploration for macromolecules. Free energy is an old concept. It is de-

ﬁned as a function of a set of coarse-grained variables. Until recently it was limited

412 CHAPTER 9. PROBLEMS WITH MULTIPLE TIME SCALES

to a very small number of such variables. Recent techniques such as metadynamics

and temperature-accelerated molecular d ynamics have made it possible to explore

the space of many coarse-grained variables [28, 34].

4. The application of the Mori-Zwanzig formalism to molecular dynamics [9, 32].

To begin with, what would be a good choice of the coarse-grained variables? Well,

the answer depend s on the purpose of the simulation. If the purpose is to understand

the mechanism of some chemical reaction, then the coarse-grained variables should be

able to serve as reaction coordinates. This issue will be discussed in Chapter 10. If

the interest is the macroscopic behavior of the system, then the coarse-grained variables

should be a complete set of the slow variables of the system, since in that case, the

time scale separation between the coarse-grained (slow) variables and the variables that

are eliminated allows us to make satisfactory approximations without the need to keep

memory terms. If the interest is the behavior of a speciﬁc set of variables, such as the

variables that describe the dynamics around a local defect, then we have no choice but

to include these variables in the set of coarse-grained variables and model the memory

eﬀects (see for example [32]).

As an example, we will discuss the version of the CGMD proposed by Rudd and

Broughton [37]. Starting with a Hamiltonian dynamics:

= ∇

= −∇

H (9.3.1)

where j = 1, 2, ··· , N,

H =

j=1

+ V (x

, x

, ··· , x

) (9.3.2)

we deﬁne a set of coarse-grained variables:

α,j

, P

α,j

(9.3.3)

for some choices of {f

α,j

}, where α = 1, ··· , K. In the Rudd-Broughton version of the

CGMD, the coarse-grained variables obey Hamiltonian dynamics

= ∇

= −∇

H (9.3.4)

9.3. COARSE-GRAINED MOLECULAR DYNAMICS 413

with the coarse-grained Hamiltonian:

H(X

, ··· , X

; P

, ··· , P

) (9.3.5)

Z Z

−βH

δ(X

−

α,j

)δ(P

−

α,j

)Π

j=1

where β = 1/k

T , Z is the partition function: Z =

−βH

j=1

. (9.3.5) is

the equilibrium distribution projected to the submanifold deﬁned by the coarse-grained

variables.

When V is a quadratic function:

V (x

, ··· , x

) =

j,k

(9.3.6)

then a direct computation gives

H =

α,β

+ X

α,β

+ 3(N − K)k

T (9.3.7)

where

α,β

= m

α,k

β,k

−1

(9.3.8)

α,β

j,k

α,j

−1

j,k

β,k

−1

{

} and {P

} are related by

α,β

(9.3.9)

This formalism can obviously be generalized to the case when the coarse-grained

variables are deﬁned by nonlinear functions. However, there are two main diﬃculties

with this approach.

1. The ﬁrst is whether Hamiltonian dynamics with (9.3.5) as the Hamiltonian is a good

approximation to the dynamics of the coarse-grained variables. (9.3.4) and (9.3.5)

assumes that there is a separation of the time scales between the dynamics for the

coarse-grained variables and the relaxation dynamics of the remaining degrees of

freedom. The accuracy of the approximation depends on the diﬀerence between

these two time scales.

414 CHAPTER 9. PROBLEMS WITH MULTIPLE TIME SCALES

2. On the practical side, it is not easy to evaluate the coarse-grained Hamiltonian H

and its derivatives. Analytical evaluation seems only feasible for the case when V

is quadratic. Add ing cubic terms to V makes the calculation much harder [38].

To illustrate the importance of the ﬁrst issue, let us consider the following example

[23]:

H =

+ x

+ p

) (9.3.10)

The Hamilton’s equations are:

= p

= −x

− x

(9.3.11)

= p

= −x

− x

If we regard (x

, p

) as variables for some thermal bath and use CGMD to eliminate

, p

), we obtain a system for the remaining variables (x

, p

= p

= −x

− x

E(x

, x

) (9.3.12)

where the conditional expectation is given by

E(x

, x

) =

−H

1 + x

(9.3.13)

Therefore the CGMD system is:

= p

= −q

−

1 + q

(9.3.14)

However, the behavior of this system is quite diﬀerent from the behavior of the original

system, even after averaging over diﬀerent initial conditions of x

and p

(using the

equilibrium distribution, conditioned on (x

, p

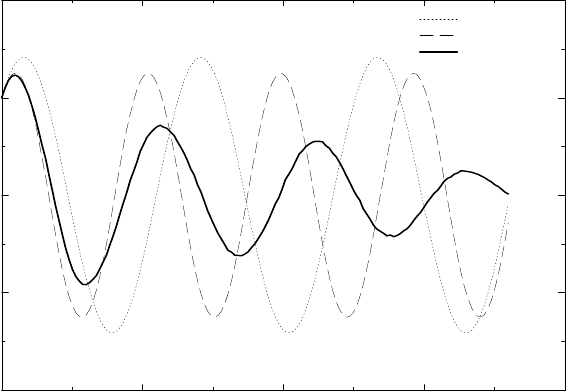
) been ﬁxed), as can be seen from Figure

9.4. In particular, the dissipative eﬀect in the original system, due to the fact that energy

in (x

, p

) is transferred t o the bath variables (x

, p

), is lost in the new system (9.3.14).

As was pointed out in [23], this error is caused by the drastic approximation used

in (9.3.5), which becomes quite inaccurate in non-equilibrium situations. To reduce this

kind of error, one has to take into account the memory and noise eﬀect, as can be seen

in the Mori-Zwanzig formalism (see Section 2.7). This is a general issue, which we will

return to in Chapter 11.

9.3. COARSE-GRAINED MOLECULAR DYNAMICS 415

0.0 5.0 10.0 15.0 20.0

Time

−1.0

−0.5

0.0

0.5

1.0

E[phi_1(t)|phi_1(0),phi_2(0)]

Galerkin

Averaging

Truth

Figure 9.4: Comparison of the ensemble-averaged solution (solid line) of the original

Hamiltonian system and the coarse-grained Hamiltonian system for the model problem

(9.3.10) (courtesy of Alexandre Chorin) [10]. The dashed line is the solution to the coarse-

grained molecular dynamics. The dotted line is the solution to the truncated system in

which the un resolved component is simply set to 0. The quality of the two solutions are

just about equally bad.

416 CHAPTER 9. PROBLEMS WITH MULTIPLE TIME SCALES

We now turn to the second diﬃculty. One way of overcoming this diﬃculty is to

formulate CGMD using the extended Lagrangian formulation [35]. This was done by

Iannuzzi, Laio and Parrinello [25]. The idea is to extend the phase-space to include the

coarse-grained variables as additional dynamic variables. For simplicity, we will follow

[14] and consider the case of overdamped dynamics:

x = −∇V (x) +

2β

−1

w (9.3.15)

in the conﬁguration space instead of MD in the phase space.

Assume that the coarse-grained variables are deﬁned by

X = q(x) = (Q

(x), Q

(x), ··· , Q

(x)) (9.3.16)

The equilibrium density for X is given by

¯ρ(X) =

−1

−βV (x)

δ(X − q(x))dx (9.3.17)

The question is how to compute this function eﬃciently.

The idea in [25] is to consider the energy in the extended space of variables (x, X):

V (x, X) = V (x) +

µ|X − q(x)|

, (9.3.18)

where µ > 0 is a parameter to be prescribed later. Introducing another friction parameter

γ, we can formulate the overdamped dynamics associated with (9.3.18):







x = −∇V (x) + µ(X − q(x))∇q(x) +

2γβ

−1

X = −µ(X − q(x)) +

2β

−1

(9.3.19)

where

W are independent white-noises.

For all γ > 0, the equilibrium density for (9.3.19) is

(x, X) = Z

−1

−βV (x)−

µβ|X−q(x)|

, (9.3.20)

where Z is a normalization factor such that the total integral of ρ

is 1. The corresponding

marginal density of X is

¯ρ

(X) = Z

−1

−βV (x)−

µβ|X−q(x)|

dx (9.3.21)