Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

8.3. SUBLINEAR SCALING ALGORITHMS 377

Neumann formulation

In this case, the microscale problem is formulated as







−∇ · (a

(x)∇)ϕ = 0, in I

(x)∇ϕ(x) · n = λ · n, on ∂I

(8.3.14)

where the constant vector λ ∈ R

is the Lagrange multiplier for the constraints

h∇ϕi = G. (8.3.15)

The eﬀective conductivity tensor is then given by

(x)∇ϕi = A

∗

h∇ϕi = A

∗

G. (8.3.16)

For example when d = 2, to solve problem (8.3.14) with the constraint (8.3.15), we

ﬁrst solve for ϕ

and ϕ

from







−∇ · (a

(x)∇ϕ

) = 0, in I

(x)∇ϕ

(x) · n = µ

· n, on ∂I

(8.3.17)

for i = 1, 2, where µ

= (1, 0)

, µ

= (0, 1)

. Given an arbitrary G, the Lagrange

multiplier λ = (λ

, λ

)

is determined by the linear equation

h∇ϕ

i + λ

h∇ϕ

i = G (8.3.18)

and the solution of (8.3.14)-(8.3.15) is given by ϕ = λ

+ λ

It is easy to see that for the 1-dimensional case, the three quantities A

∗

, A

∗

, A

∗

are

equal. In high dimensions, we have ([56])

Theorem 8.

∗

≤ A

∗

≤ A

∗

. (8.3.19)

To see the inﬂuence of the cell size and the particular boundary cond ition on the

accuracy of the eﬀective coeﬃcient tensor, [56] performed a systematic numerical study

on various examples. In particular, the two dimensional random checker-board problem

was used as a test case. This is a random two-phase composite material: The plane is

covered by a square lattice, and each square is randomly assigned one of the two phases

378 CHAPTER 8. ELLIPTIC EQUATIONS WITH MULTISCALE COEFFICIENTS

with equal probability. Both phases are assumed to be isotropic. The interest on this

problem stems from the fact that the eﬀective conductivity for this case can be computed

analytically using some d uality relations, and is found to be the geometric mean of the

conductivities of the two phases [54]. The main conclusions of this study were:

1. Periodic boundary condition performs better for both the random and periodic

problems tested.

2. In general the Neumann formulation underestimates the eﬀective conductivity ten-

sor and the Dirichlet formulation overestimates the eﬀective conductivity tensor,

consistent with the theorem mentioned earlier.

3. When computing the eﬀective tensor by averaging over the cell, the accuracy can

be improved if weighted or truncated averaging is used. In general, the results of

the weighted averaging, with smaller weights near the boundary, is more robust.

4. The variance of the estimated eﬀective conductivity tensor behaves as σ

∼ L

−2

for the random checker-board problem.

Table 8.1 gives a sample of the results for the random checker-board problem. The

exact eﬀective conductivity is 4.

8.3.3 Error estimates

To get an idea about how the method works, we follow the framework discussed in

Chapter 6 for the error analysis of HMM. Deﬁne

e(HMM) = max

ℓ

∈K,K∈T

kA(x

ℓ

) −

A(x

ℓ

)k,

where

A(x

ℓ

) is the estimated coeﬃcient at x

ℓ

using (8.3.4) and (8.3.5), A(x

ℓ

) is the

coeﬃcient of the eﬀective model. Following the general str ategies discussed for HMM in

Chapter 6, one can prove the following [25]:

Theorem 1. Assume that (8.0.1) and (8.3.1) are uniformly elliptic. Denote by U

and U

HMM

the solution of (8.3.1) and the HMM solution, respectively. If U

is suﬃciently

smooth, then there exists a constant C independent of ε, δ and H, such that

− U

HMM

≤ C (H + e(HMM)) , (8.3.20)

− U

HMM

≤ C



+ e(HMM)



. (8.3.21)

8.3. SUBLINEAR SCALING ALGORITHMS 379

Cell size 4 6 8 10 16

Number of realizations 1000 800 800 400 100

∗

4.354 4.253 4.182 4.164 4.109

∗

4.105 4.061 4.044 4.021 4.016

∗

3.790 3.838 3.848 3.883 3.925

0.619 0.295 0.153 0.090 0.035

0.645 0.267 0.153 0.093 0.038

0.502 0.204 0.134 0.080 0.030

Table 8.1: Random checker-board: Ensemble averaged eﬀective conductivities computed

using diﬀerent boundary conditions. Also shown are the results of sample variance.

This result is completely general. However, to estimate e(HMM) quantitatively, we

do need to make speciﬁc assumptions on th e structure of the coeﬃcients in (8.0.1). In

general, if we assume that a

(x) is of the form a(x, x/ε), then we have

|e(HMM)| ≤ C





(8.3.22)

where δ is the size of the computational domain for the microscale problem. The value

of the exponent α depends on the rate of convergence of the relevant homogenization

problem as well as the boundary conditions used in the microscopic problem. Some

interesting results are obtained in [34].

Error analysis of the full discretization including the eﬀect of discretization of the

microscale problem is considered in [2].

8.3.4 Information about the gradients

There is another important point to be made. So far in this section, we have empha-

sized capturing the macroscale behavior of the system. We paid little attention to what

380 CHAPTER 8. ELLIPTIC EQUATIONS WITH MULTISCALE COEFFICIENTS

happens at the microscale. In fact, we tried to get away with knowing as little as possible

about the microscale behavior, so long as we are able to capture the macroscale behav-

ior. For some applications involving (8.0.1), this is not what is needed. For example,

in the context of composite materials, we are often interested in the stress distribution

which is not captured by the eﬀective macroscale model, or the homogenized equation:

Information about stress (or the gradients) is part of the microscale details that we did

not pay much attention to. The same is true in the context of modeling multi-phase

ﬂow in porous medium. There we are also interested in the velocity ﬁeld for the purpose

of modeling the transport, and information about the velocity ﬁeld is also part of the

microscale details that we have not paid attention to.

It is possible to recover some information about the gradients from the HMM solu-

tions. Let u

be the HMM solution. Clearly, ∇u

is not going to be close to ∇u

, where

is the solution to the original microscale problem (8.0.1), since u

contains only the

macroscopic component. To recover information about the gradients, note that on each

element K ∈ T

, ∇u

is a constant vector G

= ∇u

. On K, we expect ∇φ

to contain some information about ∇u

. For example, we expect that their probability

distribution functions are close. At th is point though, this remains to be speculative

since no systematic quantitative study has been carried out on how much information

can be recovered about ∇u

from this procedure.

For the general case, having u

, one can also obtain locally the microstructural in-

formation using an idea in [47]. Assume that we are interested in recovering u

and ∇u

only in the subdomain D ⊂ Ω. Let D

be a domain with the property D ⊂ D

⊂ Ω and

dist(∂D, ∂D

) = η. Consider the following auxiliary problem:

−∇ · (a

(x)∇)˜u(x) = f(x) x ∈ D

, (8.3.23)

˜u(x) = u

(x) x ∈ ∂D

, (8.3.24)

We then have [25]



|D|

|∇(u

− ˜u)|



1/2

≤

− u

∞

)

. (8.3.25)

See [1] for a review of other relevant issues on ﬁnite elment HMM.

8.4. NOTES 381

8.4 Notes

Other approaches

There are many other related contributions that we should have included but could

not due to the lack of space. Some of these include:

• Eﬃcient use of the homogenization approach [22, 52]. In particular, Schwab and

co-workers have studied the use of sparse representation to solve eﬃciently the

homogenized models.

• Mixed formulation, see the work of [5, 20]. This is preferred in some applications

since it tends to have better conservation property.

Adaptivity

This is obviously an important issue. See [3, 47] for some initial results in this

direction. We will come back to this point at the end of the book.

Generality vs. eﬃciency

The main issue is still the conﬂict between generality and eﬃciency. Here by gener-

ality, we mean the class of problems that can be handled. The most general methods

are methods such as the classical multi-grid solver for the original microscale problem.

However, they are still too costly for many practical problems. The most eﬃcient algo-

rithms are HMM or approaches that are based on precomputing the eﬀective homogenized

equation, such as the RAV approach.

A central issue is whether one can make the former class of metho ds more eﬃcient

by taking into account the special features that the problem might have, and whether

we can make HMM type of algorithms more general.

It should be noted that when the co eﬃ cients have multiscale features, then the simple

version of the multi-grid algorithm discussed in Chapter 3 is no longer adequate, since

the choice of the coarse-grid operator discussed there does not necessarily reﬂect the

eﬀective properties on the coarse scale. How one should choose the eﬀective operators in

this case is still somewhat of an open question for general elliptic PDEs with multiscale

coeﬃcients. Some work has been reported in [28, 45].

We have discussed the case of spatial scale separation in which sublinear scaling

algorithms can be constructed. Other situations can also be contemplated. For example,

382 CHAPTER 8. ELLIPTIC EQUATIONS WITH MULTISCALE COEFFICIENTS

if we are solving a dynamic problem and the microstructure is frozen in time, or more

generally when th e microstructure changes much more slowly than the macro dynamics

of interest, then the kind of algorithms discussed in Section 8.1 such as RFB ﬁnite

element metho d and MsFEM might also be made sublinear, since the overhead involved

in formulating the ﬁnite element space (such as ﬁnding the basis functions) can be greatly

reduced. Yet another case for which sublinear scaling algorithms can be constructed is

discussed next.

Exploring statistical self-similarity

In the example discussed above, sublinear scaling was possible due to the disparity

between the macro and micro scales. Another situation for which it is possible to de-

velop sublinear scaling algorithms, and use sampling of the microscale behavior on small

domains to predict the behavior on larger scales was explored in [26]. This is the case

when the small scale components at diﬀerent scales are statistically self-similar. This

work is still quite far from being mature. Nevertheless, we will summarize it here since it

gives some interesting suggestions on how one may develop sublinear scaling algorithms

for problems without scale separation.

General strategy for data estimation. In the problems discused above and in

Section 6.3, scale separation was very important for the eﬃciency of HMM: It allows us to

work with small simulation boxes for the microscale problem and still retain reasonable

accuracy for the estimated data. Working with larger simulation boxes gives roughly the

same estimates for the data. In other words, if we denote the value of the estimated

data on a box of size L as f = f(L), then when L is above some critical size, f is

approximately independent of L:

f(L) ≈ Const (8.4.1)

Here the critical size is determined by the characteristic scale of the microscopic model,

which might just be the correlation length. This idea can be generalized in an obvious

way. As long as the scale depend ence of f = f(L) is of a simple form with a few

parameters, we can make use of this simple relationship by p er forming a few (not just

one as was done for problems with scale separation) small scale simulations and use the

results to establish an accurate approximation for th e dependence of f on L. Once we

have f = f(L), we can use it to predict f at a much larger scale.

One example of such a situation is when the system exhibits local self-similarity. In

8.4. NOTES 383

this case the dependence in (8.4.1) is of the form f (L) = C

with only two parameters

and β. Therefore we can use results of microscopic simulations at two diﬀerent values

of L to predict the result at a much larger scale, namely size of the macroscale mesh H.

Transport on a percolation network at criticality. This idea was demonstrated

in [26] on the example of eﬀective transport on a two-dimensional bond percolation

network at the percolation threshold.

In the standard two dimensional bond percolation model with parameter p, 0 ≤ p ≤ 1,

we start with a square lattice, each bond of the lattice is either kept with probability

p or deleted with probability 1 − p. Of particular interest is the size of the percolation

clusters formed by the remaining bonds in the network (see Figure 8.4 for a sample of

bond percolation). The critical value for this model is p = p

∗

= 0.5. For an inﬁnite

Figure 8.4: Bond percolation network on a square lattice at p = 0.5 (courtesy of Xingye

Yue)

lattice, if p < p

∗

, the probability of having inﬁnite size clusters is zero. For p > p

∗

, the

probability of having inﬁnite size clusters is 1. Given the parameter value p, the network

has a characteristic length scale – the correlation length, denoted by ξ

. As p → p

∗

, ξ

diverges as

∼ |p −p

∗

, (8.4.2)

where α = −4/3 (see [50]). At p = p

∗

, ξ

= ∞. In this case, the system has a continuum

distribution of scales, i.e. it has clusters of all sizes. In the following we will consider the

case when p = p

∗

384 CHAPTER 8. ELLIPTIC EQUATIONS WITH MULTISCALE COEFFICIENTS

We are interested in the macroscopic transport on such a network. To study transport,

say of some pollutants whose concentration density will be denoted by c, we embed this

percolation model into a domain Ω ∈ R

. We denote by ε the bond length of the

percolation network, and L the size of Ω. We will consider the case when ε/L is very

small.

The basic microscopic model is that of mass conservation. Denote by S

i,j

, i, j =

1, ··· , N the (i, j)-th site of the percolation network, and c

i,j

the concentration at that

site. Deﬁne the ﬂuxes

• The ﬂux from the right: f

i,j

= B

i,j

i+1,j

− c

i,j

)

• The ﬂux from the left: f

i,j

= B

i−1,j

− c

i,j

)

• The ﬂux from the top: f

i,j

= B

i,j

i,j+1

− c

i,j

)

• The ﬂux from the bottom: f

i,j

= B

i,j−1

− c

i,j

)

Here the various B’s are the bond conductivities for the speciﬁed bonds. The bond

conductivity is zero if the corresponding bond is deleted, and 1 if th e bond is kept. At

each site S

i,j

, from mass conservation, we have

i,j

+ f

i,j

+ f

i,j

+ f

i,j

= 0, (8.4.3)

i.e. the total ﬂux to this site is zero. This is our microscale model. It can be viewed as

a discrete analog of (8.0.1).

In the HMM framework, it is natural to choose a ﬁnite volume scheme over a macroscale

grid Ω

where H is the size of the ﬁnite volume cell. The data that we need to estimate

from the microscale model, here the p ercolation model, are the ﬂuxes at the mid-points

of the boundaries of the ﬁnite volume cells. Since the present problem is linear, we only

need to estimate the eﬀective conductivity for a network of size H. We note that at

p = p

∗

, the eﬀective conductivity is strongly size-dependent. In fact there are strong

evidences suggesting that [39]:

κ(L) ∼ C

(8.4.4)

for some values of β, where κ(L) is the mean eﬀective conductivity at size L.

Assuming that (8.4.4) holds, we will numerically estimate the values of β and C

. For

this purp ose, we perform a series of microscopic simulations on systems of sizes L

and

8.4. NOTES 385

, where ε ≪ L

ε < L

ε ≪ H. From the results we estimate κ(L

) and κ(L

). We then

use these results to estimate the parameter values C

, β in (8.4.4). Once we have these

parameter values, we can use (8.4.4) to predict κ(H).

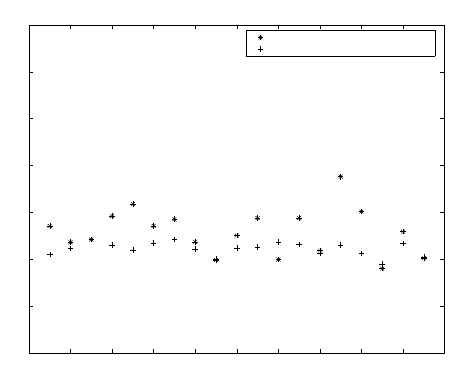
One interesting question is the eﬀect of statistical ﬂuctuations. To see this we plot

in Figure 8.6 the actual and predicted (using self-similarity) values of the conductivity

on a lattice of size L = 128 for a number of realizations of the percolation network. The

predicted values are computed using the simulated values from lattices of size L = 16

and L = 32. We see that the predicted values have larger ﬂuctuations than the actual

values, suggesting that the ﬂuctuations are ampliﬁed in the process of predicting the mean

values. Nevertheless the mean values are predicted with reasonable accuracy, considering

the relatively small size of the network.

−2

−1

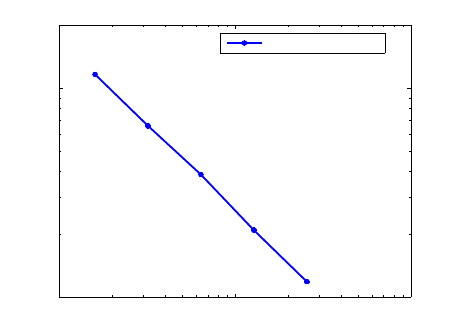
Log−log figure of effective conductivity vs size L

L=(16,32,64,128,256) ε

Figure 8.5: Eﬀective conductivity at diﬀerent scale L = (16, 32, 64, 128, 256)ε for a real-

ization of the percolation network with p = p

∗

= 0.5 (courtesy of Xingye Yue).

For more details, see [26].

The general case. In the general case when there are no special features that can

be made use of, one possibility is to use the viewpoint of model reduction, i.e. given

the operator L = −∇ · (a

(x)∇) or its discretization on a ﬁne grid, A

(where N is the

number of grid points), and given a number M (M ≪ N), one asks: What is its best

M ×M approximation

in the sense that the solutions to the equations A

u = f and

= f are the closest for a general right hand side f among all M × M matrices?

We will return to this problem in Chapter 11.

386 CHAPTER 8. ELLIPTIC EQUATIONS WITH MULTISCALE COEFFICIENTS

0 2 4 6 8 10 12 14 16 18 20

0.01

0.015

0.02

0.025

0.03

0.035

0.04

Predicted and actual conductivity for L=128

Different realizations of percolation

predicted value from L=16 and 32

acutal value

Figure 8.6: Eﬀect of ﬂuctuations: Actual and predicted eﬀective conductivity at scale

L = 128ε for diﬀerent realizations of the percolation network with p = 0.5. The predicted

values are computed from L = 16ε and 32ε lattices (courtesy of Xingye Yue).