Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

7.6. NOTES 347

Let F = (L

atom

− L

qqc

)(y

). Then

= 0, k ≤

= ε

−1

(G(2

) − G( 2D

)),

= ε

−1

(G(2

) + G(2D

−

) − 2G(2D

)),

= (L

atom

− L

)

, k ≥ 1.

(7.5.11)

Taylor expansion gives:











0, k ≤

O(1), k =

1, 0

O(ε

), k ≥ 1.

(7.5.12)

We see that the truncation error is small, except at the interface where it is O(1). Using

this fact, one can show under sharp stability conditions that the maximum error in the

deformation gradient is of O(ε). The details can be found in [33].

As we said earlier, what makes this kind of analysis possible is that the models used

in both the local and the nonlocal region can be regarded as consistent approximations to

the same continuum model. Extension of this kind of analysis to the case when statistical

errors are involved is still an open problem.

7.6 Notes

This is the most diﬃcult chapter to write, and perhaps many readers will not ﬁnd

the materials they expected to see. The diﬃculty is the following. On one hand, the

idea of developing hybrid formulations or hybrid algorithms that couple diﬀerent levels

of physical models together is extremely popular in many disciplines nowadays. On the

other hand, a lot of the existing work involves some ad hoc components in one way or

another. Except for very few cases, it is not clear how on e can assess the accuracy of

these hybrid schemes. Consequently, a description of these methodologies will inevitably

become a set of receipes rather than a coherent set of ideas with a solid foundation.

For this reason, we opt to discuss the general principles rather than the latest exciting

examples. Our selection of the gener al principles also reﬂect the desire to put things on

a solid foundation: After discussing the general coupling strategies, we chose to focus on

two classical issues in numerical analysis, namely, stability and accuracy.

348 CHAPTER 7. RESOLVING LOCAL EVENTS OR SINGULARITIES

The most unsatisfactory aspect of all this is the lack of understanding of the eﬀect

of noise or ﬂuctuations. We have seen from Ren’s work that the accumulation of noise

can lead to numerical instabilities. Bu t what about accuracy? There are examples which

demonstrate that the amplitude of the ﬂuctuations is reduced when kinetic Monte Carlo

models are replaced in part of the computational domain by deterministic continuum

equations [17, 43]. This suggests that instead of deterministic continuum models, one

should use stochastic continuum models when developing coupled atomistic-continuum

simulation methods [17, 43]. Doing this consistently is still a challenge.

Figure 7.6 is an image taken from [10] for the adiabatic piston problem. A long

quasi one-dimensional box with adiabatic walls is divided in two halves by a thermally-

insulating piston of mass M that can move along the length of the box without friction.

The two halves of the box is ﬁlled with ﬂuid particles of mass m (m ≪ M). Pressure

diﬀerence on both sides of the piston drives the piston to mechanical equilibrium, in

which the pressure diﬀerence vanishes. More interestingly, it has been understood th at

the mechanical asymmetric ﬂuctuations of the piston due to its thermal motion eventually

drives the system to thermal equilibrium, in which the temperature diﬀerence of the two

sides also vanishes. This process can in principle be simulated using molecular dynamics

or ﬂuctuating hydrodynamics. However, classical (deterministic) hydrodynamics fails to

predict the eventual full thermal equilibrium. The consequence of this is that the hybrid

method with deterministic hydrodynamics fails to predict the long term behavior of the

system accurately.

There is another diﬃculty. Take for example QM-MM methods at zero temperature.

In this case, we do not have to worry about noise. However, we still do not know how

to systematically quantify the error in QM-MM meth ods since we do not have a natural

small parameter to measure the size of the error. In classical numerical analysis, we

measure the numerical error in terms of the size of the grid. In homogenization theory,

we measure the error of the homogenized model in terms of the small parameter ε (see

Section 2.3). Here, th ere is no such a small parameter, not an obvious one at least.

7.6. NOTES 349

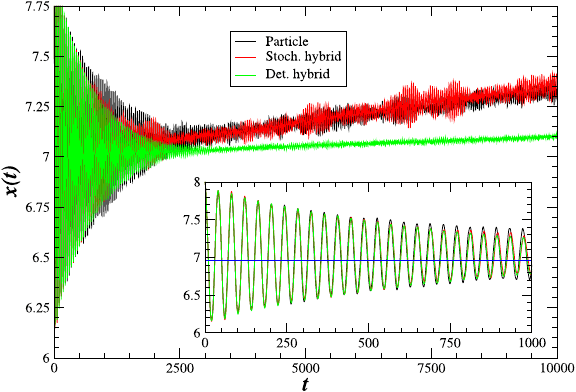
Figure 7.9: Relaxation of a massive rigid piston (M/m = 4000) which is initially not in

mechanical equilibrium. Shown in the ﬁgure is the position of the piston as a function

of time. Mechanical equilibrium is established through rapid oscillations. Both the

hybrid method with ﬂuctuating hydrodynamics and the direct particle simulation are

able to predict the very slow relaxation to the thermal equilibrium. The hybrid method

with deterministic hydrodynamics fails to do so or at least under-predicts the relaxation

rate. The inset highlights the initial oscillations and shows that in the regime where th e

ﬂuctuations do not matter the deterministic and stochastic hybrid methods agree well

(from [10], courtesy of John Bell.)

350 CHAPTER 7. RESOLVING LOCAL EVENTS OR SINGULARITIES

Bibliography

[1] F.F. Abraham, J.Q. Broughton, N. Bernstein and E. Kaxiras, “Spanning the contin-

uum to quantum length scales in a dynamic simulation of brittle fracture,” Europhys.

Lett., vol. 44, no. 6, pp. 783–787, 1998.

[2] S. Badia, P. Bochev, J. Fish, M. Gunzburger, R. Lehoucq, M. Nuggehally and M.

Parks, “A force-based blending model for atomistic-to-continuum coupling,” Intern.

J. Multiscale Comp. Engrg., vol. 5, pp. 387–406, 2007.

[3] T. Belytschko and S. P. Xiao, “Coupling methods for continuum model with molec-

ular model,” Intern. J. Multiscale Comput. Engrg., vol 1, pp. 115–126, 2003.

[4] G.A. Bird, Molecular Gas Dynamics, Oxford University Press, USA, 1976.

[5] N. Choly, G. Lu, W. E and E. Kaxiras, “Multiscale simulations in simple metals:

A density-functional based methodology,” Phys. Rev. B, vol. 71, no. 9, pp. 094101–

094101-16, 2005.

[6] P. Degond, J.-G. Liu and L. Mieussens, “Macroscopic ﬂuid modes with localized

kinetic upscaling eﬀects,” Multiscale Model. Simul, vol. 5, pp. 695–1043, 2006.

[7] R. Delgado-Buscalioni and P. V. Coveney, “Continuum-particle hybrid coupling for

mass, momentum, and energy transfers in unsteady ﬂuid ﬂow,” Phys. Rev. E, vol.

67, pp. 046704–046704-13, 2003.

[8] H. Ben Dhia, “Multiscale mechanical problems: The Arlequin method,” C. R. Acad.

Sci. IIb, vol. 326, pp. 899–904, 1998.

[9] M. Dobson and M . Luskin, “An analysis of the eﬀect of ghost force oscillation on

quasicontinuum error,” Math. Model. Numer. Anal., vol. 43, pp. 591–604, 2009.

351

352 BIBLIOGRAPHY

[10] A. Donev, J. B. Bell, A. L. Garcia, and B. J. Alder, “A hybrid particle-continuu m

method for hydrod ynamics of complex ﬂuids”, Multiscale Modeling and Simulation,

vol. 8, No. 3, pp. 871-911, 2010.

[11] W. E, B. Engquist, X. Li, W. Ren and E. Vanden-Eijnden, “Heterogeneous multi-

scale methods: A review,” Commun. Comput. Phys., vol. 2, pp. 367–450, 2007.

[12] W. E and Z. Huang, “Matching conditions in atomistic-continuum modeling of ma-

terials,” Phys. Rev. Lett., vol. 87, no. 13, pp. 135501–135501-4, 2001.

[13] W. E and J. F. Lu, “The continuum limit and the QM-continuum approximation

of quantum mechanical models of solids,” Comm. Math. Sci., vol. 5, pp. 679–696,

2007.

[14] W. E, J. Lu and Jerry Z. Yang, “Uniform accuracy of the quasicontinuum method,”

Phys. Rev B, vol. 74, pp. 214115–214115-12, 2006.

[15] W. E and P. B. Ming, “Cauchy-Born rule and the stability of the crystalline solids:

Static problems,” Arch. Rat. Mech. Anal., vol. 183, pp. 241–297, 2007.

[16] E. G. Flekkoy, G. Wagner and J. Feder, “Hybrid model for combined particle and

continuum dynamics,” Europhys. Lett, vol. 52, pp. 271–276, 2000.

[17] A. L. Garcia, J. B. Bell, W. Y. Crutchﬁeld and B. J. Alder “Adaptive mesh and

algorithm reﬁnement using direct simulation Monte Carlo,” J. Comput. Phys., vol.

154, pp. 134–155, 1999.

[18] C. Garcia-Cervera, J. Lu and W. E, “A sublinear scaling algorithm for computing

the electronic structure of materials,” Comm. Math. Sci., vol. 5, no. 4, pp. 990–1026,

2007.

[19] J. Gao, “Metho ds and applications of combined quantum mechanical and molecular

mechanical potentials,” Reviews in Computational Chemistry, vol 7, K. B. Lipkowitz,

D. B. Boyd, Eds., pp. 119–185, VCH Publishers, New York, 1995.

[20] J. Gao, P. Amara, C. Alhambra, J. J. Field, “A generalized hybrid orbital (GHO)

method for the treatment of boundary atoms in combined QM/MM calculations,”

J. Phys. Chem. A, vol. 102, pp. 4714–4721, 1998.

BIBLIOGRAPHY 353

[21] V. Gavini, K. Bhattacharya and M. Ortiz, “Quasi-continuum orbital-free density

functional theory: A route to multi-million atom non-periodic DFT calculation,” J.

Mech. Phys. Solids, vol. 55, pp. 697-718, 2007.

[22] N. Hadjiconstantinou, “Hybrid atomistic-continuum formulations and the moving

contact-line problems,” J. Comp. Phys, vol. 154, pp. 245–265, 1999.

[23] N. Hadjiconstantinou and A. T. Patera, “Heterogeneous atomistic-continuum rep-

resentation for dense ﬂuid systems,” Int. J. Modern Phys. C, vol. 8, pp. 967–976,

1997.

[24] J. Li, D. Liao and S. Yip, “Coupling continuum to molecular-dynamics simulation:

Reﬂecting particle method and the ﬁeld estimator,” Phys. Rev. E, vol. 57, pp. 7259–

7267, 1998.

[25] J. Li, D. L iao and S . Yip, “Nearly exact solution for coupled continuum/MD ﬂuid

simulation,” J. of C omputer-Aided Material Design, vol. 6, pp. 95–102, 1999.

[26] X.-T. Li and W. E, ‘Multiscale modeling of the dynamics of solids at ﬁnite temper-

ature,” J. Mech. Phys. Solids, vol. 53, pp. 1650–1685, 2005.

[27] X.-T. Li, J. Z. Yang and W. E., ”A multiscale coupling method for the modeling of

dynamics of solids with application to brittle cracks,” J. Comput. Phys., vol. 229,

no. 10, pp. 3970–3987, 2010.

[28] P. Lin, “Convergence analysis of a quasi-continuum approximation for a two-

dimemsional material without defects,” SIAM J. Numer. Anal., vol. 45, pp. 313–332,

2007.

[29] P. Lin, “Theoretical and numerical analysis for the quasi-continuum approximation

of a material particle model,” Math. Com p., vol. 72, pp. 657–675, 2003.

[30] G. Lu and E. Kaxiras, “Overview of multiscale simulations of materials,” in Hand-

book of Theoretical and Com putational Nanothechnology, vol. X, pp. 1–33, M. Rieth

and W. Schommers eds., American Scientiﬁc Publishers, Stevenson Ranch, CA,

2005.

354 BIBLIOGRAPHY

[31] R. Miller and E. Tadmor, “A uniﬁed framework and performance benchmark of four-

teen multiscale atomistic/continuum coupling methods,” Modelling and Simulation

in Material Science and Engineering, vol. 17, pp. 053001–053001-51, 2009.

[32] P. B. Ming, “Error estimates of forced-based quasicontinuum method,” Comm.

Math. Sci., vol. 5, pp. 1089–1095, 2008.

[33] P. B. Ming and J. Z. Yang “Analysis of the quasicontinuum method,” Multiscale

Model. Simul., vol. 7, pp. 1838–1875, 2009.

[34] X. Nie, S. Chen, W. E and M. O. Robbins, “A continuum and molecular dynamics

hybrid method for micro- and nano-ﬂuid ﬂow,” J. Fluid Mech., vol. 500, pp. 55–64,

2004.

[35] S. T. O’Connel and P. A. Thompson, “Molecular dynamics-continuum hybrid com-

putations: A tool for studying complex ﬂuid ﬂows,” Phys. Rev. E, vol. 52, pp.

5792–5795, 1995.

[36] J. T. Oden and K. S. Vemaganti, “Estimation of local modeling error and goal-

oriented adaptive modeling of heterogeneous materials; Part I: Error estimates and

adaptive algorithms,” J. Comput. Phys., vol. 164, pp. 22–47, 2000.

[37] C. Ortner and E. S¨uli, “Analysis of a quasicontinuum method in one dimension,”

ESAIM M2AN, vol. 42, pp. 57–92, 2008.

[38] H. S. Park, E. G. Karp ov, W. K. Liu and P. A. Klein, “The bridging scale for

two-dimensional atomistic/continuum coupling,” Phil. Mag. A, vol. 85, pp. 79–113,

2005.

[39] W. Ren, “Analytical and numerical study of coupled atomistic-continuum methods

for ﬂuids,” J. Comput. Phys., vol. 227, pp. 1353–1371, 2007.

[40] W. Ren and W. E, “Heterogeneous multiscale method for the modeling of complex

ﬂuids and micro-ﬂuidics,” J. Comp. Phys., vol. 204, pp. 1–26, 2005.

[41] R. D. Richtmyer and K. W. Morton, Diﬀerence Schemes for Initial Value Problems,

Interscience Publishers, New York, 1967.

BIBLIOGRAPHY 355

[42] R.E. Rudd and J.Q. Broughton, “Coarse-grained molecular dynamics and the atomic

limit of ﬁnite elements,” Phys. Rev. B, vol. 58, no. 10, pp. R5893–R5896, 1998.

[43] T. Schulze, P. Smereka and W. E, “Coupling kinetic Monte-Carlo and continuum

models with application to epitaxial growth,” J. Comput. Phys., vol. 189, no. 1, pp.

197–211, 2003.

[44] V.B. Shenoy, R. Miller, E.B. Tadmor, R. Phillips and M. Ortiz, “An adaptive ﬁnite

element approach to atomic scale mechanics-the quasicontinuum method,” J. Mech.

Phys. Solids, vol. 47, pp . 611–642, 1999.

[45] T. Shimokawa, J.J. Mortensen, J. Schiøz and K.W. Jacobsen, “Matching cond itions

in the quasicontinuum method: Removal of the error introduced in the interface

between the coarse-grained and fully atomistic region,” Phys. Rev. B, vol. 69, pp.

214104–214104-10, 2004.

[46] U. C. Singh, P. A. Kollman, “A combined abinitio quantum-mechanical and molec-

ular mechanical method for carrying out simulations on complex molecular systems

applications to the CH3Cl + Cl- exchange-reaction and gas-phase p rotonation of

polyethers,” J. Comput. Chem., vol. 7, pp. 718–730, 1986.

[47] G. Strang, “Accurate partial diﬀerence methods; Part II: Non-linear problems,”

Numer. Math, vol. 6, pp. 37–46, 1964.

[48] E. B. Tadmor, M. Ortiz and R. Phillips, “Quasicontinuum analysis of defects in

crystals,” Philos. Mag. A, vol. 73, pp. 1529–1563, 1996.

[49] A. Toselli and O. Widlund, Domain Decomposition Methods, Springer, 2004.

[50] A. Warshel, M. Karplus, “Calculation of ground and excited state potential surfaces

of conjugated molecules; Part I: Formulation and parametrization,” J. Am. Chem.

Soc., vol. 94, pp. 5612–5625, 1972.

[51] A. Warshel and M. Levitt, “Theoretical studies of enzymic reactions,” J. Mol. Biol.,

vol. 103, pp. 227–249, 1976.

[52] T. Werder, J. H. Walther, J. Asikainen and P. Koumoutsakos, “Continuum-particle

hybrid methods for dense ﬂuids,” in Multiscale Modeling and Simulation, vol. 39, pp.

356 BIBLIOGRAPHY

35–68, edited by S. Attinger and P. Koumoutsakos, Lecture Notes in Computational

Science and Engineering, Springer, 2004.

[53] T. Werder, J. H. Walther and P. Koumoutsakos, “Hybrid atomistic-continuum

method for the simulation of dense ﬂuid ﬂows,” J. Comp. Phys., vol. 205, pp. 373–

390, 2005.

[54] Y. Zhang, T.-S. Lee and W. Yang “A pseudobond approach to combining quantum

mechanical and molecular mechanical methods,” J. Chem. Phys., vol. 110, pp. 46–

54, 1999.