Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

8.1. MULTISCALE FINITE ELEMENT METHODS 367

where C

and C

are constants independent of ε and H. When the over-sampling tech-

nique is used, (8.1.31) can be improved to [27]:

− ˜u

(Ω)

≤ C

Hkfk

(Ω)

+ C

√

ε (8.1.32)

8.1.5 Relations between the various metho ds

It is quite obvious that the RFB ﬁnite element method is closely related to VMS: As

was pointed out already in [40, 41], the RFB ﬁnite element method can be viewed as a

special case of VMS in which the bubble functions represent the ﬁne scale component of

the solution.

The relation b etween the RFB ﬁnite element method and MsFEM has also been in-

vestigated [18, 51, 55]. The most thorough discussion is found in [55]. We now summarize

its main conclusions.

We split the bubble component into two parts u

= M

) + M(f), such that

), M(f) ∈ V

, and

a(u

+ M

), v) = 0, for all v ∈ V

(8.1.33)

a(M(f), v) = (f, v), for all v ∈ V

. (8.1.34)

Roughly speaking M

) is the intrinsic part of the bubble component due to the mul-

tiscale structure of the coeﬃcients in the PDE (8.0.1), M(f) is the part of the bubble

component due to the forcing term.

Let K ∈ T

. In (8.1.16), let f = 0, u

= ϕ

K,j

. Then u

= M

(ϕ

K,j

). (8.1.16) becomes

L(ϕ

K,j

+ M

(ϕ

K,j

)) = 0, on K (8.1.35)

with the boundary condition M

(ϕ

K,j

) = 0 on ∂K. Compared with (8.1.28), we see that

if φ

K,j

satisﬁes the boundary condition (8.1.29), then we must have

K,j

= ϕ

K,j

+ M

(ϕ

K,j

) (8.1.36)

A similar statement also holds for the numerical solutions, namely

˜u

= u

+ M

) (8.1.37)

if the bilinear form a is symmetric. Here u

, ˜u

are respectively the coarse component

of the numerical solution of the RFB method and the solution of MsFEM. This can be

368 CHAPTER 8. ELLIPTIC EQUATIONS WITH MULTISCALE COEFFICIENTS

seen as follows. With the notations deﬁned above, we can reformulate the RFB ﬁnite

element method as

a(u

+ M

) + M (f), v

) = (f, v

), for all v

∈ V

a(u

+ M

) + M (f), v

) = (f, v

), for all v

∈ V

Letting v

= M

) in the second equation and adding the two equations, we obtain

a(u

+ M

) + M (f), v

+ M

)) = (f, v

+ M

)), for all v

∈ V

(8.1.38)

If the bilinear form a(·, ·) is symmetric, then from (8.1.33),

a(M(f), v

+ M

)) = a(v

+ M

), M(f)) = 0 (8.1.39)

Therefore

a(u

+ M

), v

+ M

)) = (f, v

+ M

)), for all v

∈ V

. (8.1.40)

Together with (8.1.36), we obtain (8.1.37).

It should be noted that both the RFB ﬁnite element method and MsFEM have been

extended to situations when a(·, ·) is unsymmetric. In that case, (8.1.37) may not hold.

For a discussion on the connection between variational multiscale method and Ms-

FEM, please see [6].

8.2 Upscaling via successive elimination of small scale

components

In many situations, we are interested in ﬁnding an eﬀective model for the large scale

component of the solution. In some cases, su ch models can be obtained analytically, using,

for example, the techniques discussed in Chapter 2. However, analytical app roaches are

often quite limited. They rely on very special features such as periodicity of the small

scale structure of the problem. Therefore, it is of interest to develop numerical techniques

for deriving such eﬀective models, i.e., for the purpose of upscaling. The objective then is

to eliminate the small scale components. At an abstract level, such a procedure has been

discussed at the end of Chapter 2. However, many practical issues have to be resolved

in order to implement this procedure eﬃciently.

8.2. UPSCALING VIA SUCCESSIVE ELIMINATION OF SMALL SCALE COMPONENTS369

To begin with, we can either eliminate the small scales in one step or do it successively.

Using the notation in Chapter 3, if we write

u =

k=1

and choose to keep only the components with k ≤ K

, we can use one of the following

two approaches:

1. Eliminate the components

k=K

in one step. Using the notation of Chapter

2, this can be done by choosing H

to be the space that contains the components

we would like to keep, and perform the procedure discussed at the end of Chapter

2. Eliminate the small scale components successively, i.e. we ﬁrst eliminate u

, then

N−1

, u

N−2

, and so on.

Our experience with the renormalization group analysis suggests that the second ap-

proach is more preferrable in general. The main reason is that with the second approach,

each step is a perturbation of the previous step. Therefore it is more likely that the

eﬀective operator only changes slightly at each step. This is important when making

approximations on the eﬀective op erators. For this reason, we will focus on the second

approach, which was initially suggested by Beylkin and Brewster [15], and has been pur-

sued systematically by Dorobantu, Engquist, Runborg, et al. [23, 4]. A nice review can

be found in [29].

The basic idea is to implement the scale elimination procedure outlined at the end

of Chapter 2 in a multi-resolution framework. For this purpose, we need a sequence of

multi-resolution subspaces of L

, as discussed in Chapter 3. The sequence of subspaces

generated by wavelets is a natural choice, even though other choices are also possible. In

renormalization group analysis, for example, one often chooses the Fourier spaces.

Recall the basic setup for multi-resolution analysis:

[

, (8.2.1)

where

j+1

= V

⊕ W

, W

= V

⊥

(8.2.2)

370 CHAPTER 8. ELLIPTIC EQUATIONS WITH MULTISCALE COEFFICIENTS

To start the upscaling procedure, one ﬁrst chooses a V

and discretize the original

problem (8.0.1) in V

. V

should be large enough to resolve the ﬁne scale details of the

solution of (8.0.1). After discretization, one obtains a linear system of equations:

= f

(8.2.3)

Let u

= u

, A

= A

, f

= f

. In V

, deﬁ ne P

as the projection operator to the

subspace V

−1

, and Q

= I−P

. Write u

= u

−1

where u

−1

= P

, w

−1

. Using th e basis functions in V

−1

and W

−1

, one can rewrite (8.2.3) as:



−1







(8.2.4)

Eliminating w

−1

, one obtains:

− A

)

−1

= f

− A

)

−1

(8.2.5)

Let A

−1

= A

− A

)

−1

, f

−1

= f

− A

)

−1

, one can then rep eat the

above procedure.

One obvious problem with the procedure described so far is the following. Our original

operator was a diﬀerential operator and therefore one expects the matrix A

obtained

from ﬁnite diﬀerence or ﬁnite element discretizations to be sparse. This property is

lost after the elimination step, since (A

)

−1

is in general a full matrix and so is A

−1

Fortunately, even though A

−1

is full, many of its components are very close to zero,

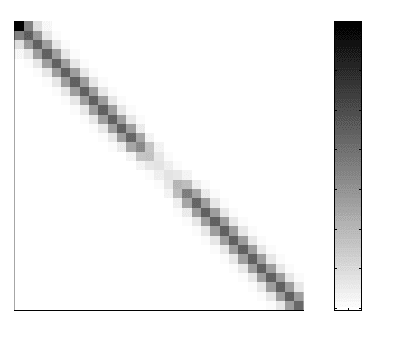
due to their fast decay property, as shown in Figure 8.1. The decay rate in the wavelet

representation was analyzed systematically in [16]. See also [29]. Therefore one should be

able to approximate the matrix A

−1

by a sparse matrix and still retain good accuracy.

Two ways of approximating the matrix A

−1

have been proposed and tested. The ﬁrst

is a direct truncation to banded or block-banded matrix. For one dimensional problems,

this is done as follows. Given a matrix A, deﬁne a new banded matrix trunc(A, ν) of

bandwidth ν by:

trunc (A, ν)







, if 2|i − j| ≤ ν − 1

0, otherwise

(8.2.6)

For higher dimensional problems, one should consider block-banded matrices (see [29]).

The second approach is to project the matrix A

−1

to the space of banded (or block-

banded) matrices, with the constraint t hat the action of the original matrix and the

8.2. UPSCALING VIA SUCCESSIVE ELIMINATION OF SMALL SCALE COMPONENTS371

1000

2000

3000

4000

5000

6000

7000

5 10 15 20 25 30

Figure 8.1: The structure of the matrices obtained during the elimination process (cour-

tesy of Olof Runborg).

projected matrix be the same on some special subspaces, e.g. subspaces representing

smooth functions. This is called band projection.

In principle, there is a third possibility, namely, thresholding: If a matrix element is

less than a prescribed threshold value, it is set to 0. This is less practical, since one does

not have a priori control of the sparsity pattern in such an approach.

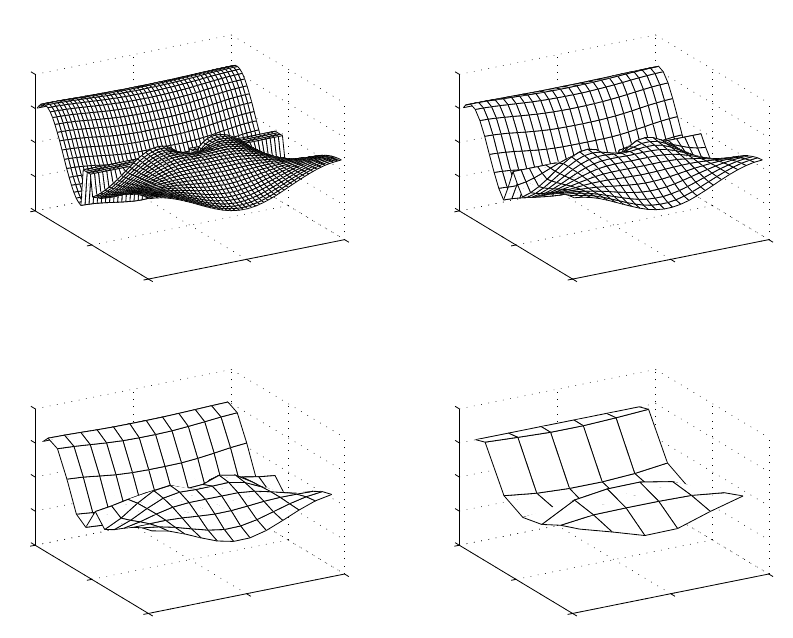
An example of the numerical solutions obtained using this successive scale elimination

procedure is shown in Figure 8.2.

The pr ocedure described above is an example of the numerical homogenization tech-

niques. It has been applied to several diﬀerent classes of problems, including elliptic

equations with multiscale coeﬃcients, Helmholtz equations, as well as some hyperbolic

and nonlinear problems (see [29]). It has a close resemblance to the renormalization

group procedure. Its main advantage is its generality: There are no special requirements

on either the PDE or the multiscale structure. Nevertheless, it requires starting from

a fully resolved numerical discretization. Therefore, the best one can hope for is a lin-

ear scaling algorithm. In addition, information about the small scale components of the

solution is lost during the process. For example, in the context of stress analysis of com-

posite materials, special eﬀorts have to be made to recover information about the stress

distribution.

372 CHAPTER 8. ELLIPTIC EQUATIONS WITH MULTISCALE COEFFICIENTS

0.5

−2

−1

Original

0.5

−2

−1

1 homogenization

0.5

−2

−1

2 homogenizations

0.5

−2

−1

3 homogenizations

Figure 8.2: An example of the numerical solutions of the Helmholtz equation obtained

after successively eliminating the smalls scales, see [29]

8.3. SUBLINEAR SCALING ALGORITHMS 373

8.3 Sublinear scaling algorithms

The approaches discussed above are all linear or super-linear scaling algorithms. Take

the example of the homogenization problem with periodic coeﬃcients (8.0.1): a

(x) =

a(x, x/ε). In their current formulation, the overhead for forming the ﬁnite element spaces

in GFEM, RFB ﬁnite element, VM S and MsFEM all scales as 1/ε

or more, where d is

the spatial dimension of the problem. The cost for forming the ﬁne scale discretization

operator in the numerical homogenization procedure that we just discussed also scales as

1/ε

. In some applications, algorithms with such a cost are not feasible and one has to

look for more eﬃcient techniques, i.e. sublinear scaling algorithms.

As we explained in the ﬁrst chapter, we can not expect to have sublinear scaling

algorithms for completely general situations. We have to rely on special features of the

problem, such as separation of scales, or similarity relations between diﬀerent scales. In

other words, the problem has to have a special structure in th e space of scales. This

special structure allows us to make predictions on larger scales based on information

gathered from small scale simulations, therefore achieving sublinear scaling. For the

problems treated here, the heterogeneous multiscale method (HMM) discussed in Chapter

6 provides a possible framework for developing such algorithms. We will discuss two

situations for which sublinear scaling algorithms can be developed. The ﬁrst is the case

with scale separation. The second, discussed in the notes, is the case when the small

scale features exhibit statistical self-similarity.

There is another reason for designing algorithms such as HMM which focus on small

windows: For practical problems, we often do not have the full information about the

coeﬃcients everywhere in the physical domain of interest. In the context of sub-surface

porous medium modeling, for example, we often have rather precise information locally

near the wells, and some coarse and indirect information away from the wells. The per-

meability and porosity ﬁeld s used in porous medium simulations are obtained through

geostatistical modeling. This is also a source of signiﬁcant error. Therefore it might be

of interest to consider the reversed approach: Instead of ﬁrst performing geostatistical

modeling on the coeﬃcients and solving the resulting PDE, one may develop algorithms

for predicting the solution by using only the data that are obtained directly from mea-

surements. HMM can be viewed as an example of such a procedure.

374 CHAPTER 8. ELLIPTIC EQUATIONS WITH MULTISCALE COEFFICIENTS

8.3.1 Finite element HMM

To setup HMM, we need to have some idea about how t he macroscale model looks

like. In the case of (8.0.1), abstract homogenization theory tells us that the macroscale

component of the solution satisﬁes an eﬀective equation of the form [14]:

−∇ · (A(x)∇U(x)) = f(x), x ∈ D (8.3.1)

where A(x) is the eﬀective coeﬃcient at the macroscale. These coeﬃcients are not ex-

plicitly known. It is possible to precompute them. But if we are interested in a strategy

that works equally eﬀectively for more complicated situations such as nonlinear or time-

dependent problems, we should compute them “on-the-ﬂy”.

As the macro-solver, it is natural to use the standard ﬁnite element method. The

simplest choice is the standard C

piecewise linear element, on a triangulation T

where

H denotes the element size. We will denote by V

the ﬁnite element space. The size of

the elements should resolve t he macroscale computational domain D, but they do not

have to resolve the small scales.

The needed data is the stiﬀness matrix for the ﬁnite element method:

A = (A

) (8.3.2)

where

(∇Φ

(x))

A(x)∇Φ

(x) dx (8.3.3)

and A(x) is the eﬀective coeﬃcient (say, the conductivity) at th e scale H, {Φ

(x)} are

the standard n odal basis functions of V

. Had we known A(x), we could evaluate (A

)

by numerical quadrature. Let f

(x) = (∇Φ

(x))

A(x) · ∇Φ

(x), then

(x)dx ≃

K∈T

|K|

ℓ

∈K

ℓ

) (8.3.4)

where {x

ℓ

} and {w

ℓ

} are the quadrature points and weights respectively, |K| is the volume

of the element K. Therefore the data that we need to estimate are the values of {f

ℓ

)}.

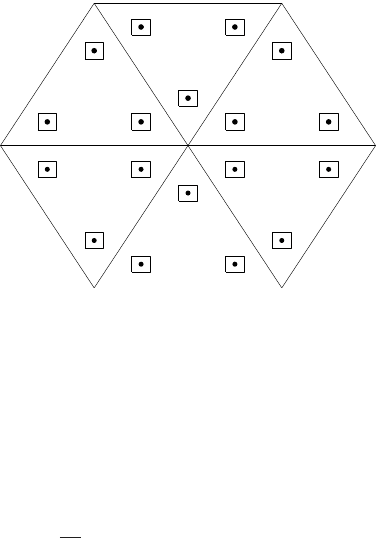
This will be done by solving the original microscopic model, properly reformulated, locally

around each quadrature point {x

ℓ

} on the domain I

ℓ

), as shown in Figure 8.3.1.

The key component of this method is the boun dary condition for the microscale

problem (8.0.1) on I

ℓ

). This will be discussed in the next subsection.

8.3. SUBLINEAR SCALING ALGORITHMS 375

Figure 8.3: Illustration of HMM for solving (8.0.1). The dots are the quadrature points. The

little squares are the microcell I

ℓ

From the solution to the microscale problem, we estimate the needed data f

ℓ

) by

ℓ

) ≃

ℓ

)

(∇ϕ

(x))

(x)∇ϕ

(x) dx (8.3.5)

where ϕ

is the solution to the microscale problems on I

ℓ

) that correpond to Φ

(more

precise formulation will be discussed below)

− ∇(a

(x) · ∇)ϕ

(x) = 0 (8.3.6)

h∇ϕ

= ∇Φ

ℓ

) (8.3.7)

and similarly for ϕ

. Knowing {f

ℓ

)}, we obtain the stiﬀness matrix A by (8.3.4).

8.3.2 The local microscale problem

We now come to the boundary conditions for the local microscale problem. Ideally,

one would like to formulate the boundary conditions in such a way as if the boundary

was not present, i.e. we would like to capture exactly the microscale solution on I

(see

Chapter 7), which is the solution of the microscale problem over the whole macroscale

domain restricted to I

. This is not possible, due to the intrinsic nonlocality of the

elliptic equations. Still, we would like to minimize the error due to the artiﬁcial boundary

conditions.

376 CHAPTER 8. ELLIPTIC EQUATIONS WITH MULTISCALE COEFFICIENTS

To formulate the local microscale problem on I

, we ask the question: If the average

gradient is G, what is the corresponding microscale b ehavior? To answer this question,

we solve the microscale problem (8.3.6) subject to the constraint

h∇ϕ

= G (8.3.8)

We will denote the solution to the microscale problem with the constraint (8.3.8) by ϕ

This problem was investigated in [56]. Below is a summary of the ﬁndings in [56]. Three

diﬀerent types of boundary conditions were considered.

Dirichlet formulation

In this case, Dirichlet boundary condition is used for the local microscale problem







−∇ · (a

(x)∇ϕ) = 0, in I

ϕ(x) = G · x, on ∂I

(8.3.9)

One can check easily that

h∇ϕ(x)i ≡

−

∇ϕ(x)dx ≡

∇ϕ(x)dx = G. (8.3.10)

In the Dirichlet formulation the eﬀective cond uctivity tensor A

∗

is deﬁned by the relation

(x)∇ϕi = A

∗

h∇ϕi = A

∗

G. (8.3.11)

Periodic formulation

In this case, the microscale problem is given by:







−∇ · (a

(x)∇)ϕ = 0, in I

ϕ(x) − G · x is periodic with period I

(8.3.12)

It can be easily checked that the constraint (8.3.8) is satisﬁed. The eﬀective conductivity

tensor A

∗

is deﬁned through

(x)∇ϕi = A

∗

h∇ϕi = A

∗

G. (8.3.13)

It is obvious that when the micro-structure of a

is periodic, A

∗

will be the same as

the homogenized coeﬃcient tensor obtained in the homogenization theory ([57], see also

Section 2.4) if I

is chosen to be an integer multiple of the period.