Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

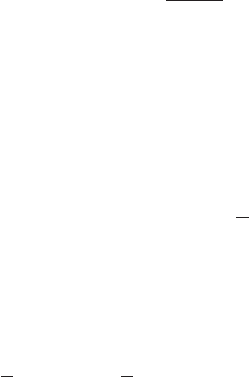
7.4. STABILITY ISSUES 337

This lemma can be proved by ind uction. It is enough to consider the upper half

channel due to the symmetry assumption. Consider the VV coupling scheme for example.

In the ﬁrst iteration, one starts with an equilibrium MD in the p-region. The average

velocity at y = a is denoted by ξ

, and is used as the Dirichlet boundary condition for the

continuum model in the c-region. The steady state solution of the continuum equation

(7.1.12) with the boundary condition u(L) = 0 and u(a) = ξ

is given by

(y) = ξ

L − y

L − a

= ξ

V V

(y) (7.4.8)

This proves (7.4.1) for n = 1. Assume that (7.4.1) is valid for the n-th iteration. In

the (n + 1)-th iteration, the MD in the p-region is constrained so that the mean particle

velocity at y = b is equal to u

(b) =

i=1

n−i

V V

g(b). Therefore the average velocity in

the p-region in the (n + 1)-th iteration is given by

˜u

n+1

(y) = u

(b)

+ η

(y)

where η

(y) denotes the random ﬂuctuations in the averaged velocity. Therefore, if we

let ξ

n+1

= η

(a), we have

n+1

(a) = u

(a)

+ ξ

n+1

g(a)

i=1

n−i

V V

+ ξ

n+1

i=1

n+1−i

V V

(7.4.9)

The solution to the continuum equation with boundary condition u(a) = u

n+1

(a), u(L) =

0 is then given by

n+1

(y) = u

n+1

(a)g

V V

(y) =

n+1

i=1

n+1−i

V V

(y). (7.4.10)

This proves (7.4.1) for the (n + 1)-th iteration.

Following a similar procedur e, one can prove the lemma for the other three coupling

schemes.

Note that the ampliﬁcation factors can also be computed using a much simpler pro-

cedure, by replacing the MD by the continuum model, which in this case becomes:

∂

u = 0 (7.4.11)

For example, for the VV coupling scheme, this results in the following deteriministic

domain decomposition method: At the n-th iteration,

338 CHAPTER 7. RESOLVING LOCAL EVENTS OR SINGULARITIES

1. one ﬁrst solves the continuum equation (7.4.11) in the c-region with boundary

condition u

(a) = ˜u

n−1

(a), u

(L) = 0 t o obtain u

, and

2. one then solves the continuum equation (7.4.11) in the p-region with the boundary

condition ˜u

(b) = u

(b), ˜u

(0) = 0 to obtain ˜u

To ﬁnd the ampliﬁcation factor for such an iterative process, we look for solutions of this

problem in the form:

(y) = k

U(y), ˜u

(y) = k

U(y)

It is easy to see that U and

U must be of the form:

U(y) = C

U(y) =

L − y

L − a

From the boundary conditions at y = a, b, we get

k =

L − b

L − a

C =

Similarly, one can compute the ampliﬁcation factors for the VF, FV, and FF schemes.

Let us try to understand what these analytical results tell us. First note that according

to the size of the ampliﬁcation factor, we can put the four coupling schemes into three

categories:

1. The FF scheme. In this case, we have k

F F

= 1. If we assume that the {ξ

}’s are

independent, then we have

(y)

1/2

∼

√

nσ|g(y)|

where σ = hξ

1/2

. The important fact is that the error grows like

√

n due to the

random ﬂuctuations.

2. The VV and FV scheme. Since |k

V V

|, |k

F V

| < 1, in both cases, we h ave

(y)

1/2

≤ Cσ|g(y)|

i.e. the error is bounded. This is the best situation as far as stability is concerned.

3. The VF scheme, for which the ampliﬁcation factor satisﬁes |k

V F

| > 1. We will show

later that this is an artifact of using T

= ∞. For practical values of T

, |k

V F

| is

usually less than 1. Therefore this case should be combined with the second case.

7.4. STABILITY ISSUES 339

Now we consider the case when T

is ﬁn ite. We can also deﬁne the ampliﬁcation

factor. For example, for the VV coupling scheme, on e simply has to replace the continuum

equation (7.4.11) by a time-dependent version:

ρ∂

u = µ∂

and the boundary conditions by:

(a, t) = ˜u

n−1

(a, T

), ˜u

(b, t) = u

(b, T

To compute the ampliﬁcation factor, we look for solutions that satisfy:

(y, T

) = k

U(y), ˜u

(y, T

) = k

U(y).

In this case, it is much simpler to compute k numerically (we refer to [39] for the details

on how to compute k), and the results are shown in Figure 7.6 for all four coupling

schemes:

0 200 400 600 800 1000

0.5

, k

10 30 50 70 90

0.8

0.9

1.1

, k

Figure 7.6: The ampliﬁcation factor k versus T

/∆t for the four schemes: VV (squares),

FV (diamonds), VF (triangles) and FF (circles) (courtesy of Weiqing Ren).

340 CHAPTER 7. RESOLVING LOCAL EVENTS OR SINGULARITIES

In general, we are interested in the case when T

∼ ∆t, i.e. when we exchange data

after a small number of macro time steps. In this case, the results in Figure 7.6 agree

with the ones discussed earlier when T

= ∞, except for the VF coupling scheme: If T

is not too large, the VF coupling scheme is quite stable.

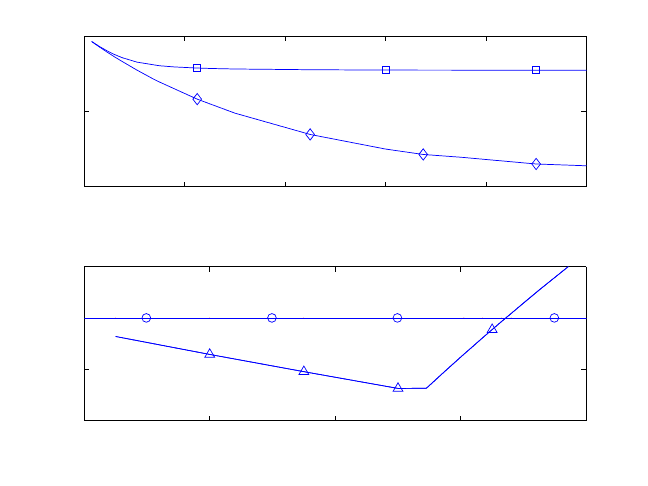
These predictions are very well conﬁrmed by the numerical results presented in [39]

for more general situations. In particular, it was found that the FF coupling scheme does

lead to large error. Consider an impulsively started shear ﬂow with constant pressure

gradient. A term of the form ρf with f = 2 × 10

−3

(in atomic units) is added to the

right hand side of the continuum equation. In the MD region, besides the inter-molecular

forces, the ﬂuid particles also feel the external force f = (f, 0, 0). The numerical results

for the case when T

= ∆t and t = 1500 obtained using the FV and FF coupling schemes

are shown in Fig. 7.7. We see from the bottom panel that the error eventually grows

roughly linearly, and the mean velo city proﬁle becomes discontinuous, as shown in th e

middle panel. Note that the setup is changed slightly: The particle regions are at the

boundary and the continuum region is now in the middle.

7.5 Consistency issues illustrated using QC

In general, the issue of consistency in a coupled multi-physics algorithm should be

examined at two diﬀerent levels:

1. Consistency between the diﬀerent physical models when they are used separately for

systems for which they are all su pposed to be adequate. For example, a continuum

elasticity model and an atomistic mod el should produce approximately the same

result, when they are used for analyzing the mechanical response of an elastically

deformed single crystal material.

2. Consistency at the interface where the diﬀerent physical models are coupled to-

gether. In general it is inevitable that coupling introduces extra error. One main

task for formulating good coupling schemes is to minimize this error.

An example of such coupling error is the ghost force in the nonlocal quasicontinuum

method (QC). In what follows, we will use this example to illustrate the origin of the

coupling error, what their consequences are and how to reduce this error.

7.5. CONSISTENCY ISSUES ILLUSTRATED USING QC 341

−100 −50 0 50 100

0 2000 4000 6000 8000

0.1

0.2

t / T

Figure 7.7: Upper and middle panel: Numerical solutions of the channel ﬂow driven by

the pressure gradient at t = 1500, obtained using the FV scheme (up per panel) and the

FF scheme (middle panel) respectively. The dashed curve is the reference solution. The

oscillatory curves at the two ends are the numerical solution in the p-region; the smooth

curve in the middle is the numerical solution in the c-region. Lower panel: The error of

the numerical solution versus time. The two curves correspond to the FV scheme (lower

curve) and the FF scheme (upper curve) respectively. From [39].

342 CHAPTER 7. RESOLVING LOCAL EVENTS OR SINGULARITIES

0 5 10 15 20 25 30 35

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

0.6

−x)

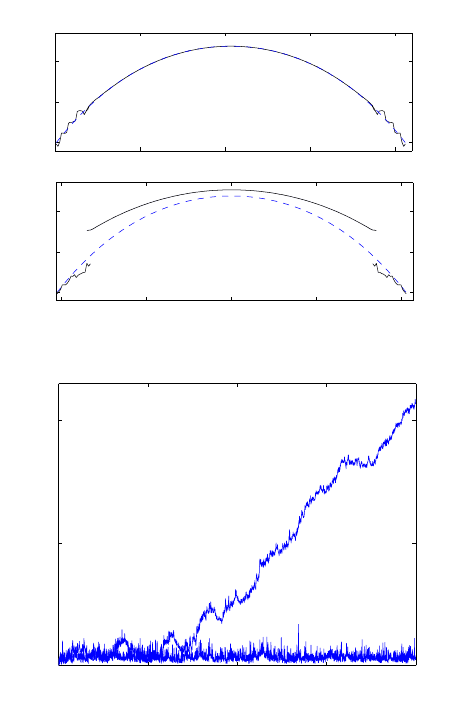
Figure 7.8: Error in deformation gradient for the original QC with next nearest neigh-

borhood quadratic interaction potential. From [33].

A very important question is how to quantify this error. We will see th at in the

case of QC, we can use a simple generalization of the notion of local truncation error to

quantify the error due to the mismatch between the diﬀerent models at the interface.

To best illustrate the heart of the matter, we will focus on the one dimensional model

problem discussed in Section 7.2. We assume that there exists a smooth function f(x)

such that

f(x

) = f

, j = ···

1, 0, 1, 2, ··· (7.5.1)

where f

is the external force acting on the j-th atom.

7.5.1 The appearance of the ghost force

First, let us consider the simplest case when there are no external forces, f = 0.

The exact solution should be given by: y

= x

for all j, i.e. the atoms should be in

their equilibrium positions. Obviously this solution does satisfy the equations (7.2.4).

However, this is no longer true for QC. Indeed, it is easy to see that if we substitute

= x

(for all j) into the QC equations (7.2.11), we have

(x)

= −

G(2)

2ε

, L

(x)

G(2)

, L

(x)

= −

G(2)

2ε

The force that appears at the right hand side is called the ghost-force [48]: They are

entirely the artifact of the numerical method.

7.5. CONSISTENCY ISSUES ILLUSTRATED USING QC 343

The origin of this ghost force is intuitively quite clear: The inﬂuence between atoms

in the local and nonlocal regions is unsymmetric. For the example discussed here, y

inﬂuences the energy associated with the atom indexed by

1, but not the other way

around.

The error induced by the ghost force can be analyzed explicitly in the case when the

interaction potential is harmonic, as was done in [33] (see also [9] for a more streamlined

argument). This explicit calculation tells us several things:

1. The deformation gradient has O(1) error at the interface.

2. The inﬂuence of the ghost force decays exponentially fast away from the interface.

3. Away from an interfacial region of width O(ε|log(ε)|), the error in the deformation

gradient is of O(ε).

The large error at the interface is a concern [33, 31]. In realistic situations, it is

conceivable that artiﬁcial defects may appear as a result of the ghost force. In any case,

it is of interest to design modiﬁcations of Q C in order to eliminate or reduce the ghost

force.

7.5.2 Removing the ghost force

Force-based ghost force removal

The simplest idea for removing the ghost force is a force-based approach [44]. In this

approach, one deﬁnes

fqc

(y))







atom

(y))

if j ≤ 0

(y))

if j ≥ 1

The deformed positions of the atoms are found by solving:

fqc

(y) = f (7.5.2)

Quasi-nonlocal QC

The force-based approach discussed above does not admit a variational formulation,

i.e. there is no un derlying energy. Shimokawa et al [45] introduced the concept of

344 CHAPTER 7. RESOLVING LOCAL EVENTS OR SINGULARITIES

quasi-nonlocal atoms, which are interfacial atoms. When computing the energy, a quasi-

nonlocal atom acts like a nonlocal atom on the nonlocal side of the interface, and like

a local atom on th e local side of the interface. As we will see below, if the inter-atomic

interaction is limited to the next nearest neighbors as in the case we are considering, the

quasi-nonlocal tr eatment of the interfacial atoms is suﬃcient for removing the ghost-force.

For the simple example considered here, the quasi-nonlocal atoms are the atoms

indexed by

1 and 0, whose energies are computed using

(V (r

) + V (r

) + V (2r

)) (7.5.3)

(V (r

) + V (r

1,0

) + V (r

1,2

) + V (2r

1,2

)) (7.5.4)

The energies for the other atoms are calculated in the same way as before for QC (see

(7.2.7)). Similarly, the Euler-Lagrange equations are the same as before for the original

QC, except for atoms indexed by

1, 0:

−

(G(r

) + G(r

) + G(2r

)) = f

, (7.5.5)

−

(G(r

) + G(r

)G(2r

) + G(r

0,1

) + 2G(2r

0,1

)) = f

Again following [33], we will write them in a compact form as:

qqc

(y) = f (7.5.6)

It is straightforward to check that there are no ghost forces, i.e. when f = 0, the

Euler-Lagrange equations are satisﬁed with y = x.

Introducing quasi-nonlocal atoms is only suﬃcient when the inter-atomic interaction is

limited to the next nearest neighbors. For the general case, E, Lu and Yang introduced the

notion of geometrically consistent schemes, which contain the quasi-nonlocal construction

as a special case [14].

7.5.3 Truncation error analysis

In classical numerical analysis, the standard way of analyzing the errors in a dis-

cretization scheme for a diﬀerential equation is to study the truncation error of the

scheme, which is deﬁned as the error obtained when an exact solution of the diﬀerential

7.5. CONSISTENCY ISSUES ILLUSTRATED USING QC 345

equation is substituted into the discretization scheme. If in addition the scheme is stable,

then we may conclude that the error in the numerical solution is of the same order as

the truncation error [41].

In general, it is unclear how to extend this analysis to multi-physics problems, as

remarked earlier. However, QC provides an example for which the classical truncation

error analysis is just as eﬀective. The main reason is that the models used in the local

and nonlocal regions can both be considered as consistent numerical discretizations of

the same continuum model, the elasticity model obtained using the Cauchy-Born rule.

The fact that this holds for the local region is obvious. The fact that this holds for

the atomistic model in the nonlocal region requires some work, and this was carried out

in [15]. For this reason, we will focus on the truncation error at the interfacial region

between the local and nonlocal regions. Note that the ghost force is the truncation error

for the special case when f = 0.

Deﬁnition. Let y

be the solution of the atomistic model (7.2.5). We deﬁne th e

truncation error F = (··· , F

, F

, ···) as

= (L

atom

− L

)(y)

, k = ··· ,

1, 0, 1, 2, ··· (7.5.7)

where L

stands for the Euler-Lagrange operator for the diﬀerent versions of QC.

It is now a simple matter to compute the truncation error for the various QC schemes

that we have discussed. The results are as follows [33].

Truncation error of the original QC

Let F = (L

atom

− L

)(y

). Then we have

= 0, k ≤

= 2ε

−1

G(2

= ε

−1

(G(2

) − 2G(2D

)),

= ε

−1

(−

G(2

) + G(2

) + 2G(2D

−

) − 2G(2D

)),

= (L

atom

− L

)

= ε

−1

(G(2

k+1

) − G( 2

k−1

) − 2G(2D

) + 2G(2D

−

)), k ≥ 2.

where

D, D

−

and D

are the central divided diﬀerence, backward divided diﬀerence

and forward divided diﬀerence operators respectively. Straightforward Taylor expansion

346 CHAPTER 7. RESOLVING LOCAL EVENTS OR SINGULARITIES

gives:











0, k ≤

O(1/ε), k =

1, 0, 1

O(ε

) k ≥ 2.

(7.5.8)

Truncation error of the force-based QC

Let F = (L

atom

− L

fqc

)(y

). Then

= 0, k < 0,

= (L

atom

− L

)

, k ≥ 0.

For k ≥ 0, we can write F







0, k ≤

, k ≥ 0

where

= G(2

) + G(2

k−1

) − 2G(2D

k−1

Using Taylor expansion, we have

= ε



′′



(1 + t)D

k−1

+ (1 − t)D



δt



)

k−1

− ε



′′



(1 + t)D

k−1

+ (1 − t)D

k−2



δt



)

k−2

= ε



′′



(1 + t)D

k−1

+ (1 − t)D



δt



)

k−2

− ε



′′′



(1 + t)D

k−1

+ (1 − t)D

(sy

+ (1 − s)y

k−2

)



dsδt



× (D

)

k−2

+ y

k−1

)(D

)

k−2

. (7.5.9)

This gives Q = O(ε

). Furthermore, we also have D

= O(ε

). Therefore, we have

F = O(ε

). (7.5.10)

Truncation error of the quasi-nonlocal method