Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

7.2. ADAPTIVE MODEL REFINEMENT OR MODEL REDUCTION 327

Given the external force f = (··· , f

, f

, ···), the total energy of the atom-

istic model can be written as:

tot

−

where u

= y

− x

and

(V (y

− y

j−1

) + V (y

j+1

− y

) + V (y

− y

j−2

) + V (y

j+2

− y

)) (7.2.2)

(V (r

j−1,j

) + V (r

j,j+1

) + V (r

j−2,j

) + V (r

j,j+2

))

Here and in what follows, we use the notation: r

j,k

= y

− y

There is an obvious problem here: For an inﬁnite system, this energy is usually

inﬁnite. In reality, the system of interest is always ﬁnite and we should supp lement the

problem with some boundary conditions. However, we will simply ignore this problem

since our main interest is really the forces acting on the atoms, not the total energy.

The Euler-Lagrange equation for the minimization of E

tot

is given by:

−(G(y

− y

j−1

) + G(y

− y

j−2

) + G(y

− y

j+1

) + G(y

− y

j+2

)) = f

(7.2.3)

−



∂



− y

j−1



+ ∂



− y

j−2



+ ∂



− y

j+1



+ ∂



− y

j+2





= f

(7.2.4)

for j = ··· ,

1, 0, 1, 2, ···. We will write this in a compact form:

atom

) = f (7.2.5)

For the nonlocal QC, we assume that the local region consists of atoms indexed by

the integers j ≥ 0, the nonlocal region consists of atoms indexed by negative integers.

The region with x ≥ 0 will be treated using a piecewise linear ﬁnite element method,

with each atom being a vertex. We will denote the j- th element [x

, x

j+1

] by I

. The

total energy of the system can be written as:

= E

local

+ E

nonlocal

+ E

int

−

328 CHAPTER 7. RESOLVING LOCAL EVENTS OR SINGULARITIES

where E

nonlocal

is the total potential energy due to the atoms in the nonlocal region,

summed over the atoms:

nonlocal

j<0

local

is the contribution from the local region, which is a sum over all the elements

local

j≥0

is the contribution of the potential energy from the element I

, computed using the

Cauchy-Born rule:

= V (r

j,j+1

) + V (2r

j,j+1

) (7.2.6)

int

is the additional contribution from the local-nonlocal interface, i.e. the atom with

index 0. Since the interaction between this atom with the atoms in the local region

is already taken into account by the Cauchy-Born rule, we only have to consider the

interaction with the atoms in the nonlocal region. This gives

int

(V (r

) + V (r

))

The interfacial region can be larger, depending on the range of the inter-atomic potential

and the details of the QC algorithm.

We can also rewrite the total energy as a sum over contributions from each atom:

−

where

= E

j−1

+ e

) (7.2.7)

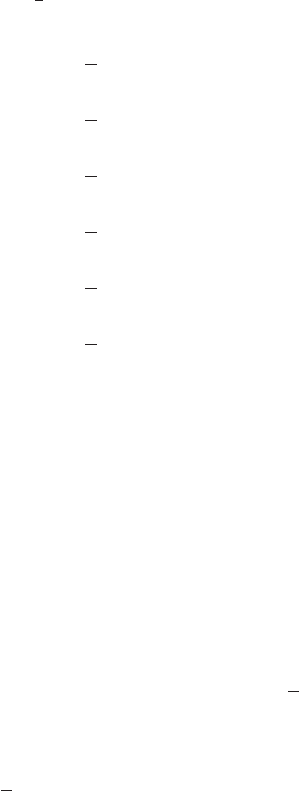
7.2. ADAPTIVE MODEL REFINEMENT OR MODEL REDUCTION 329

for j > 0, and

+ E

int

. For example:



V (r

) + V (r

)



, (7.2.8)



V (r

) + V (r

)





V (r

) + V (r

1,0

) + V (r

1,1

)





V (r

) + V (r

0,1

) + V (2r

0,1

)



(V (2r

0,1

) + V (r

0,1

) + V (r

1,2

) + V (2r

1,2

)) ,

(V (2r

1,2

) + V (r

1,2

) + V (r

2,3

) + V (2r

2,3

)) . (7.2.9)

The Euler-Lagrange equations are the same as (7.2.4) for j ≤ −1. For j ≥ 2, we have

(y)

= f

where

(y)

= −(G(r

j,j−1

) + G(r

j,j+1

) + 2G(2r

j,j−1

) + 2G(2r

j,j+1

)) (7.2.10)

For j = −

1, 0, 1, we have

− (G(r

) + G(r

G(r

)) = f

− (G(r

) + G(r

0,1

) + G(2r

0,1

)) = f

− (

G(r

) + G(r

1,0

) + G(r

1,2

) + 2G(2r

1,0

) + 2G(2r

1,2

)) = f

As before, we will write these equations in a compact form as

(y) = f. (7.2.11)

It is quite obvious that nonlocal QC can be thought of both as an adaptive model

reﬁnement procedu re and as an adaptive model reduction or coarsening procedure. As an

adaptive model reﬁnement procedure, one starts with an adaptive ﬁnite element method

for a Cauchy-Born-based continuum model. Near defects, the mesh should be reﬁned to

the atomic level and at the same time, one replaces the Cauchy-Born rule by the full

atom model. As an adaptive model reduction procedure, one starts with a full atomic

330 CHAPTER 7. RESOLVING LOCAL EVENTS OR SINGULARITIES

model and coarsens the full atom representation to a rep-atom representation. Away

from the interface, one also makes t he approximation that the deformation is locally

homogeneous, i.e. one approximates the full atom summation by the Cauchy-Born rule.

Compared with the example of ﬂuids discussed in the last subsection, QC is much

simpler due to the absence of statistical ﬂuctuations. However, consistency errors still

exist at the interface. The simplest and most well-known form of the consistency error

is the “ghost force”, i.e. forces that act on the atoms when they are in the equilibrium

position. These forces are the result of numerical error. We will come back to this

problem later in this chapter.

7.2.2 Coupled gas dynamic-kinetic models

Our next example is continuum gas dynamics locally corrected near shocks by the

kinetic model. The macroscopic model is the gas dynamics equation, say the Euler’s

equation. The microscopic model is a kinetic equation such as the Boltzmann equation

or the BGK model (see Chapter 4). We will assume that the Euler and the kinetic

equations are consistent in the sense that Euler’s equation is obtained from the kinetic

equation under the local equilibrium approximation. As the macroscale solver, it is

natural to choose the kinetic scheme for Euler’s equation (see Chapter 6). Recall that

this is a ﬁnite volume scheme with numerical ﬂuxes computed using (6.1.19). This will

help to guarantee consistency between the Euler’s equation and the kinetic equation even

at the numerical level.

Near the shocks the numerical ﬂuxes are computed by solving directly the kinetic

model using micro time steps. Consider a one-dimensional example. Assume that the

interface is located at x

k+1/2

, with Euler’s equation solved on the left side of x

k+1/2

and

the kinetic equation solved on the right side of x

k+1/2

. For the kinetic equation, we need

a boundary condition when v > 0. It is natural to choose

f(x, v, t) = M(x

−

k+1/2

, v, t), v > 0 (7.2.12)

where the right hand side is the local Maxwellian corresponding to the macroscopic state

at x

k+1/2

, where superscript “−” means that left limit is taken. The numerical ﬂux at

7.2. ADAPTIVE MODEL REFINEMENT OR MODEL REDUCTION 331

Figure 7.3: Schematics for the coupled kinetic-gas dynamics simulation: A ﬁnite volume

method is imposed everywhere in the x − t domain. The numerical ﬂuxes are computed using

the kinetic scheme away from the shocks, and directly from the solutions of the kinetic equations

around the shocks. The shaded regions indicate where the kinetic equation needs to be solved.

The left panel illustrates the case when there is no scale separation between the relaxation time

scale inside the shock and the hydrodynamic time scale. The right panel shows the case when

there is time scale separation [11].

k+1/2

is computed using:

k+1/2

∆t

n+1

M(x

−

k+1/2

, v, t)













−

f(x

k+1/2

, v, t)













(7.2.13)

The ﬁnal component of the method is a criterion for locating the kinetic region. In

principle, we would like to have something like the a posteriori error estimators discussed

in Chapter 3 to help locating kinetic regions. At the present time, little has been done in

this direction. As a working scheme, one may simply use the size of the local gradients

as the local err or indicator. If it is above certain threshold, we make it a shock region or

kinetic region.

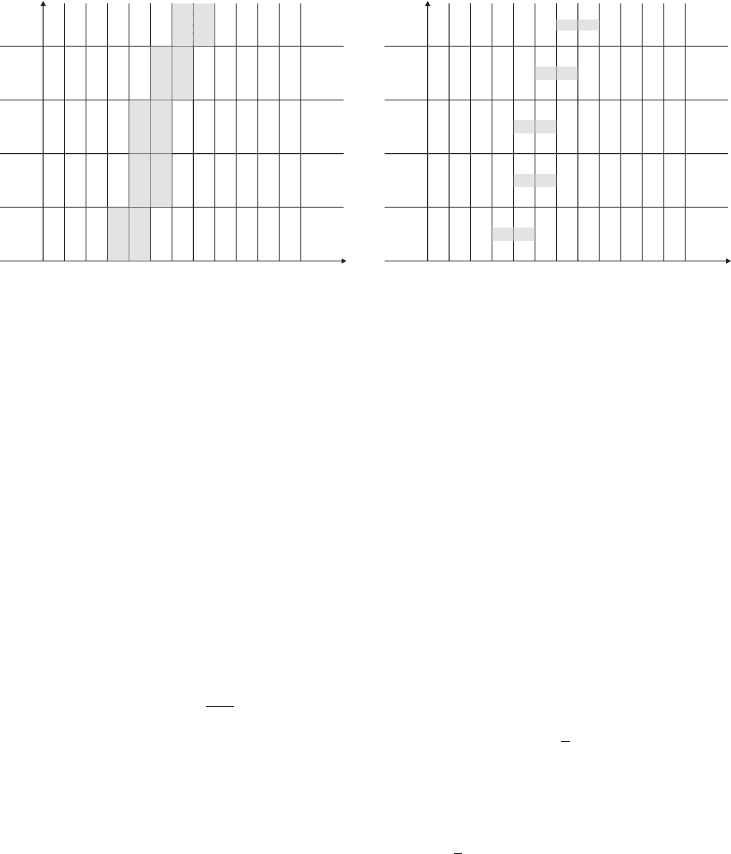
An example of numerical results computed using this method is shown in Figure 7.4

[11]. Here the result from the kinetic equation is taken as the exact solution. Note that

332 CHAPTER 7. RESOLVING LOCAL EVENTS OR SINGULARITIES

0 0.2 0.4 0.6 0.8 1

0.5

1.5

2.5

0 0.2 0.4 0.6 0.8 1

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

Figure 7.4: Numerical results for the shock tube problem: solid line – results of the kinetic

equation; ‘o’ – results of the coupled kinetic/gas dynamics simulation; ‘+’ – results of the gas

dynamics equation. Note that the coupled approach gives shock proﬁles that are more accurate

than that of the gas dynamics equation (courtesy of Xiantao Li).

7.3. THE HETEROGENEOUS MULTISCALE METHOD 333

the coupled kinetic-Euler equation gives more accurate shock proﬁles than the Euler’s

equation.

For this one dimensional example, one may solve the kinetic equation using ﬁnite

diﬀerence or other deterministic grid-based methods. For high dimensional problems, it

might be advantageous to use discrete simulation Monte Carlo methods [4], as was done

in [17].

Again we may regard the strategy discussed above either as an adaptive model re-

ﬁnement strategy, or as an adaptive model reduction strategy. Indeed, the macroscopic

model used in the region away from the shocks can be regarded as the simpliﬁcation of

the kinetic equation under the local equilibrium approximation.

7.3 The heterogeneous multiscale method

In some cases, we are only interested in getting the right macroscale behavior, not so

much about the microscopic details near the defects or singularities. In this situation,

HMM might be a good choice. One starts with a macro-solver that covers the whole

computational domain. The information needed about th e structure or dynamics of the

defects in order to und erstand the macroscale beh avior is extracted from microscopic

simulations near the defects. Such a strategy has been applied to several examples,

including the dynamics of the moving contact line [40] and the interaction of elastic

waves with crack dynamics [27] (see also [26] for a description of the main ideas in the

algorithm).

In the moving contact line problem, the macroscale behavior of interest is the dynam-

ics of the two-phase ﬂow, modeled by equations of the form:











ρ(∂

u + ∇ · (u ⊗ u)) + ∇p = µ∆u + ∇ · σ + f

∇ · u = 0

= u ·

(7.3.1)

where

σ = −γ(I −

n ⊗

n)δ

(7.3.2)

models surface tension force along the ﬂuid-ﬂuid interface Γ, γ is the surface tension

coeﬃcient,

n is the unit normal vector along Γ, δ

is the surface delta function associated

334 CHAPTER 7. RESOLVING LOCAL EVENTS OR SINGULARITIES

Repulsive Force

Sampling Region

Constrained MD

G G H H’

C’

Ι ΙΙ

D’

G’

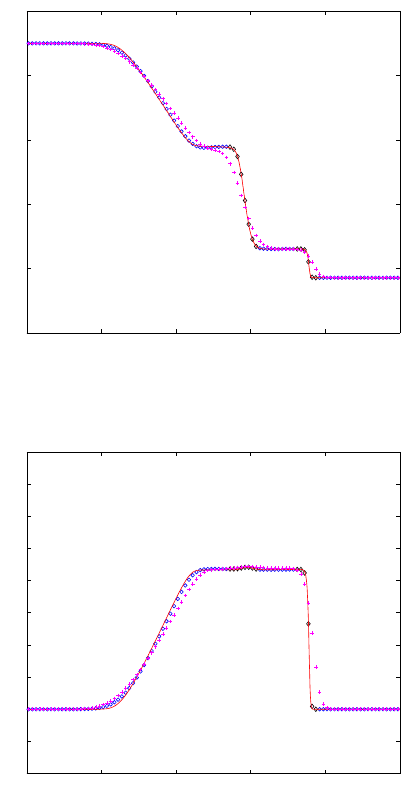
Figure 7.5: Schematic of the multiscale method for the contact line problem. Macro grid

used in the computation is represented by dotted lines in the left panel. MD is carried

out in a local region around the contact line. The dynamics in the sh aded strips GD, DC

and CH are constrained by continuum velocity ﬁeld. The shear stress and the position

of the contact point are computed in the strip along GH. From [40].

with Γ. f is some external forcing. The last equation of (7.3.1) says that the ﬂuid-ﬂuid

interface is advected by the velocity ﬁeld of the ﬂuid, v

is the normal velocity.

The data that need to be estimated from microscopic models such as MD are:

1. shear stress near the contact line,

2. velocity of the contact line, which provides the boundary condition for the dynamics

of Γ.

The schematics is shown in Figure 7.3. See [40] for details.

Compared with adaptive model reﬁnement, HMM might provide a more eﬀective way

of handling the case when the relaxation time of t he local defects τ

is much smaller than

the time scale for interesting dynamics in the local region, t

. This is possible, even

for type A problems, since τ

is governed by microscopic processes whereas t

depends

on external driving force. In this case, HMM provides a natural setting for capturing

the correct local structure around the defects, without the need to follow exactly the

microscopic dynamics.

In the same spirit, one can also extend the seamless strategy discussed in the last

chapter to this case.

7.4. STABILITY ISSUES 335

Once a general strategy is chosen, the questions to be addressed next are: Which data

are going to be exchanged between the macro and micro models and how the exchanged

data are used? The most important concern when addressing these questions is the

consistency between the macro and micro models at the interface where the two models

meet. The coupling scheme should not create signiﬁcant artifacts or numerical errors at

the interface. However, this is not the only concern. As we see below, numerical stability

might also be an issue.

7.4 Stability issues

We will focus on the domain decomposition strategy, since this is the simplest coupling

strategy. We have seen in Chapter 3 that the domain decomposition method may not

converge if we do not exchange data b etween the diﬀerent domains in the right way, since

some components of the error are not damped d uring the iteration. This has important

consequences in a multiscale, multi-physics context.

To illustrate this point, we will discuss the work of Ren [39] who considered coupled

atomistic-continuum models of ﬂuids based on the domain decomposition method. Using

a very simple example, Ren demonstrated that the performance of the coupled scheme

depends very much on how data are exchanged between the atomistic and continuum

models. Some coupling schemes lead to numerical instabilities.

The general setup of the domain decomposition-based coupling strategy was intro-

duced already in Section 7.1. Our focus is the four coupling schemes discussed : The VV,

VF, FV and FF schemes.

To begin with, let us note that the domain decomposition method considered here is

diﬀerent from the domain decomposition method discussed in Chapter 3 in at least two

aspects:

1. The p-region is usually much smaller than the c-region. This means that L ≫ b.

2. One can not avoid statistical error.

We will see later that these diﬀerences have important consequences.

Let us ﬁrst consider the simplest case when:

1. The system of interest is in equilibrium. Therefore the mean velocity should be

zero. Of course the velocities of the individual particles in the p-region will not be

336 CHAPTER 7. RESOLVING LOCAL EVENTS OR SINGULARITIES

zero, neither will the averaged velocity obtained from simulations, due to statistical

ﬂuctuations.

2. We assume reﬂection symmetry with respect to the (x, z)-plane for the coupled

scheme. Therefore the mean velocity on the (x, z)-plane vanishes.

3. T

= ∞. This means th at we only exchange data after the results of each simulation

(the continuum model or the MD) have reached (statistical) steady state.

4. We will also assume that the (spatio-temporal) averaged velocity ˜u in t he p-region

is linear in y plus some rand om ﬂuctuations. Similarly we will assume that the

averaged shear stress in the p-region is constant plus random ﬂuctuations. This is

the case if the eﬀective constitutive relation is linear. As we said earlier, this is a

very good approximation in the regime we are considering.

Admittedly, this is a very idealized case. But as we will see below, the results obtained

are already quite instructive.

Lemma 7. [39]. Under these assumptions, the numerical solutions of the coupled scheme

have the following form:

(y) =

i=1

n−i

g(y) (7.4.1)

where u

(·) is the velocity at the n-th iteration in the c-region. ξ

is the statistical er-

ror int roduced in the boundary condition at the i-th iteration. k, the ampliﬁcation (or

damping) factor, is given for the diﬀerent coupling schemes by:

V V

L − b

L − a

, (7.4.2)

F V

a − L

, (7.4.3)

V F

b − L

, (7.4.4)

F F

= 1. (7.4.5)

The function g(·) is given by:

V V

(y) = g

F V

(y) =

L − y

L − a

, (7.4.6)

V F

(y) = g

F F

(y) = y − L. (7.4.7)