Weinan E. Principles of Multiscale Modeling

Подождите немного. Документ загружается.

9.1. ODES WITH DISPARATE TIME SCALES 397

This is the complement of the unit disk centered at z = 1.

Note that the stability region for the backward Euler method contains the negative

real axis. This is an important feature since the fast component of the dynamics in (9.1.9)

is of the form of (9.1.22) with λ = −1/ε. This is not just a feature of the simple model

problem such as (9.1.9), it is rather common for ODE systems that arise from chemical

kinetic models, discretization of dissipative PDEs, etc.

So far we have only discussed the simplest implicit scheme, the backward Euler

method. There are other implicit methods such as the Adams-Moulton methods and

the bacward diﬀerentiation formula. We refer to st andard ODE textbooks such as [21]

for details.

From a practical viewpoint, one disadvantage of the implicit schemes is that they are

implicit: At every time step, one has to solve a system of algebraic equations in order to

obtain the numerical solution at that time step. These algebraic equations are usually

solved by some iterative methods. While there are very eﬃcient techniques available

for solving these algebraic equations, this does represent one additional complication

compared with the explicit methods.

It is quite remarkable that one can capture the large scale behavior of solutions to stiﬀ

ODEs without the need to resolve the small scale transients, even though we are so used to

this and we tend to take it for granted. In fact, this seems to be special to systems whose

quasi-equilibrium distributions are delta functions. The same kind of philosophy does

not work for other systems for which the quasi-equilirbium distributions are non-trivial

(i.e. not delta functions), for example stochastic ODEs or highly oscillatory systems [31],

and it is unclear how useful implicit methods are for these kind of problems.

9.1.3 Stablized Runge-Kutta methods

Now we tu rn to explicit methods. As we said earlier, simple explicit schemes such

the forward Euler method are not very eﬀective for the kind of problems discussed here.

However, composite schemes, which are sometimes formed as a composition of a large

number of forward Euler steps with diﬀerent stepsizes, can be quite eﬀective. Here we

will show how one can design such schemes in the framework of explicit Runge-Kutta

methods.

398 CHAPTER 9. PROBLEMS WITH MULTIPLE TIME SCALES

Consider the mid-point rule for the ODE ˙x = f(x):

= x

∆t

f(x

) (9.1.26)

n+1

= x

+ ∆tf(x

)

When this is applied to (9.1.22), we have

n+1

= R(z)x

(9.1.27)

where z = λ∆t

R(z) = 1 + z +

(9.1.28)

R is the stability polynomial of the mid-p oint rule. Since the exact solution of (9.1.22)

satisﬁes x(t

n+1

) = e

λz

x(t

) and since

λz

− R(z) = O(z

) (9.1.29)

we see that the local error is O(∆t

) and the global error is O(∆t

). Similarly for th e

classical 4th order Runge-Kutta method, its stability polynomial is

R(z) = 1 + z +

(9.1.30)

The local error is O(∆t

) and the global error is O(∆t

The two examples given above are examples of Runge-Kutta methods that have opti-

mal accuracy, in the sense that their order of accuracy is the maximally achievable given

the number of stages (which is the same as the number of function evaluation). The

stability region for these methods is however, quite limited.

It is possible to design Runge-Kutta methods with less accuracy but much larger

stability region. This class of methods are generally referred to as “stabilized Runge-

Kutta methods”. We will discuss a particularly interesting class of stabilized Runge-Kutta

methods, the Chebychev methods [29].

Consider an s-stage Runge-Kutta method. For consistency, its stability polynomial

has to take the form

(z) = 1 + z +

k=2

(9.1.31)

i.e. the ﬁrst two terms have to match the Taylor series for e

. We would like to choose the

coeﬃcients {C

} in order to maximize the stability region of the corresponding Runge-

Kutta method. Note that our interest is mainly in the case when the spectrum of the

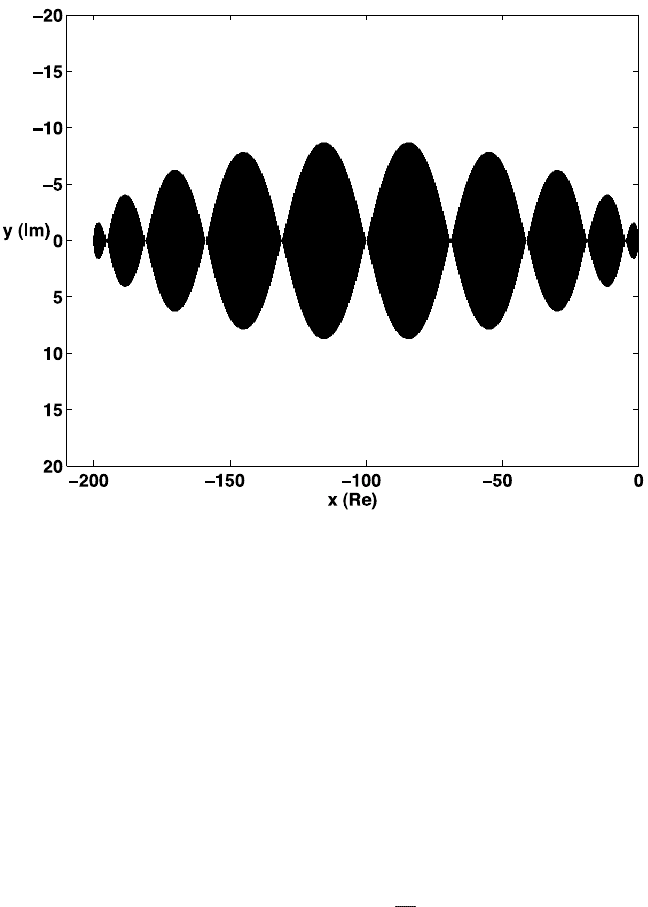
9.1. ODES WITH DISPARATE TIME SCALES 399

Figure 9.1: Stability region of the Chebychev metho d with s = 10 (courtesy of Assyr

Abdulle).

linearized ODE is located near the negative part of the real axis. Therefore our problem

can be formulated as:

Maximize l

, subject to the condition that

(−l

, 0) ⊂ {z : |R

(z)| < 1}. (9.1.32)

It is easy to see that the solution to this problem is given by

(z) = T



1 +



(9.1.33)

where T

is the Chebyshev polynomial of degree s. In this case, we have

= 2s

(9.1.34)

How do we turn this into a Runge-Kutta method? There are two ways to proceed.

The ﬁrst is to write

(z) =

j=1

(1 + c

z) (9.1.35)

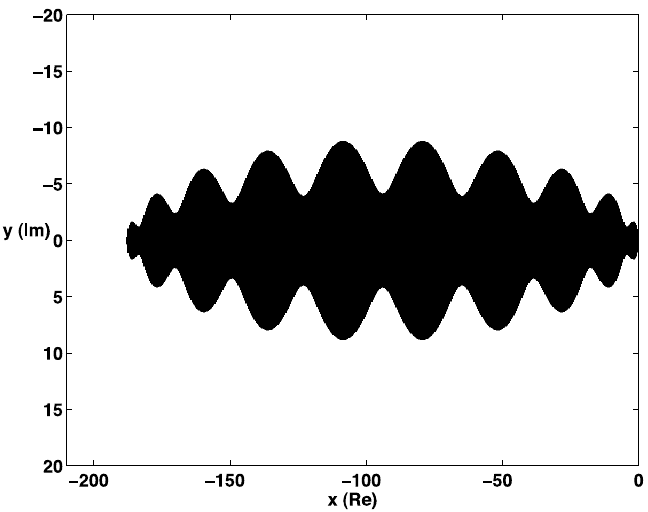
400 CHAPTER 9. PROBLEMS WITH MULTIPLE TIME SCALES

Figure 9.2: Stability region of the improved Chebychev method with s = 10, q = 0.9

(courtesy of Assyr Abdulle).

9.1. ODES WITH DISPARATE TIME SCALES 401

where the {−1/c

}’s are the roots of R

(z) which are all real and negative. Given x

, we

then form

n,0

= x

n,1

= x

n,0

+ ∆tc

f(x

n,0

)

n,2

= x

n,1

+ ∆tc

f(x

n,1

)

. . . . . .

n,s

= x

n,s−1

+ ∆tc

f(x

n,s−1

)

n+1

= x

n,s

(9.1.36)

It is easy to see that the stability polynomial of this Runge-Kutta method is given by

(9.1.33). In fact th e stability polynomial up to the k- th stage is

s,k

(z) =

j=1

(1 + c

z) (9.1.37)

This algorithm can be thought of as being a composition of forward Euler methods with

diﬀerent step sizes {c

∆t}. As such it can be regarded as a special case of the variable

time step methods. However, we prefer not to do so, partly due to the fact that when

formulated this way, the Chebyshev methods may suﬀer from the problem with internal

instabilities. Even if |R

(z)| < 1, there is no guarantee that |R

s,k

(z)| < 1 for all k. For

large s, the numerical errors might be ampliﬁed a lot in the intermediate stages before

they have a chance to be damped out eventually. This problem of internal instabilities

can be alleviated by ordering {c

} in a better way [30].

An easy way to avoid such internal instabilities is to make use of the three-term

recurrence relation for Chebyshev polynomials

n+1

(x) = 2xT

(x) − T

n−1

(x) (9.1.38)

Using this, we reformulate (9.1.36) as

n,0

= x

n,1

= x

n,0

∆t

f(x

n,0

)

. . . . . .

n,j+1

= 2x

n,j

− x

n,j−1

2∆t

f(x

n,j

)

n+1

= x

n,s

(9.1.39)

402 CHAPTER 9. PROBLEMS WITH MULTIPLE TIME SCALES

It is easy to check that if f(x) = λx, z = λ∆t, then

n,j

(z)x

(9.1.40)

where

(z) = T

(1 + z/s

), and T

is the Chebyshev polynomial of degree j. This

ensures stability for the intermediate stages, even though the scheme is no longer in the

form of a composition of forward Euler steps [24, 45].

Another point to be noted is that th e width of the stability region vanishes at the

points where T

= ±1. This is an undesirable feature. It can be avoided by replacing the

domain of consideration from {z : |R

(z)| < 1} to {z : |R

(z)| < q} where q is a positive

number less than 1. In this case R

is replaced by

(z) =

(ω

)

(ω

+ ω

z) (9.1.41)

where

= 1 +

, ω

(ω

)

′

(ω

)

(9.1.42)

The stability domain is shown in Figure 9.1.3. l

is no longer equal to 2s

. But it is still

O(s

So far, we have only discussed ﬁrst order methods. For higher order Chebyshev

methods we refer to [5, 2]. For extension to stochastic ODEs, we refer to [3, 4]. For

obvious reasons, these methods are referred to as the Chebychev methods.

Returning to the system (9.1.9) discussed earlier, we have |λ| ∼ 1/ε. If we want

∆t|λ| ≤ O(s

then we must have

∆t ≤ O(s

ε)

Since the cost per step is O(s), the total cost required to advance to O(1) time is

Cost = O





= O(

sε

)

The cost is O(1/ε) if we choose s to be O(1), and O(1) if we choose s to be O(1/ε).

In the latter case, however, the accuracy also deteriorates. Therefore th e optimal choice

depends on considerations of both accuracy and eﬃciency.

If the spectrum of the problem has a diﬀerent structure, one can design stabilized

Runge-Kutta methods accordingly. For example, if the spectrum is clustered in two

9.1. ODES WITH DISPARATE TIME SCALES 403

regions separated by a gap, one can design Runge-Kutta methods whose stability regions

cover these clusters [21, 29]. It can be shown that such stabilized Runge-Kutta methods

can be considered as compositions of forward Euler steps whose step sizes cluster into

two regions [1, 29]. In other words, they are compositions of forward Euler with small

and large time steps.

9.1.4 HMM

To illustrate the idea, let us consider the simple example (6.2.1). Here the macroscale

variable of interest is x. We will assume that its dynamics is approximated accurately

by an ODE, which can be written abstractly as:

x = F (

x, ε),

x(0) = x

(9.1.43)

with unknown right hand side,

Since the macroscale equation takes the form of an ODE, we will select stable ODE

solvers as the macro-solver. This suggests an HMM that consists of the following:

1. The macro-solver, say forward Euler:

n+1

∆t,

= x

(9.1.44)

where ∆t is the macro time step, and

denotes the approximate value of F (

, ε)

that needs to be estimated at each macro time step.

2. The micro-solver: In this case, the constrained microscale model is simply the

second equation in (6.2.1) with x = x

. In the simplest case of a forward Euler

scheme with micro time step δt, we have:

n,m+1

n,m

, t

+ mδt)δt (9.1.45)

m = 0, 1, ··· .

3. A force estimator: For example, we may use a simple time-averaging to extract

M−1

m=0

n,m

, t

+ mδt) (9.1.46)

404 CHAPTER 9. PROBLEMS WITH MULTIPLE TIME SCALES

The macroscale solver can be quite general. For example, we may also choose higher

order Runge-Kutta methods or linear multi-step methods. If we use the mid- point rule

as the macro solver, we have

n+1/2

∆t

(9.1.47)

n+1

+ ∆t

n+1/2

(9.1.48)

(9.1.49)

Here both

and

n+1/2

are unknown forces that have to be estimated from the mi-

croscale model.

One should distinguish this kind of methods from multi-time-step methods [42]. In

multi-time-step methods, diﬀerent time step sizes are used for diﬀerent terms in the

forcing. However, the detailed behavior of the model is computed accurately over the

whole time interval of interest. An illstrative example is as follows. Consider

x = f

(x) + f

(x) (9.1.50)

Assume that for some reason, we believe f

varies more slowly than f

. Then one might

use a multi-time-step integrator of the tyep:

n,0

+ ∆tf

) (9.1.51)

n,m+1

n,m

+ δtf

n,m

), m = 0, 1, ··· , M − 1 (9.1.52)

n+1

n,M

(9.1.53)

with M = ∆t/δt. In contrast, in HMM (or projective integrators for that matter), M is

determined by the relaxation time of the fast component of the dynamics.

If the ODE has a stochastic component, then the macroscale model might be in t he

form of stochastic ODEs. In this case, one should use a stochastic O DE solver as the

macro-solver in HMM. The simplest example is the Euler-Maruyama scheme:

n+1

= x

+ ∆t

+ ˆσ

√

∆tw

(9.1.54)

Now both

and ˆσ

need to be estimated. This can be done in a similar way as described

above. The details can be found in [11].

In the same spirit, seamless HMM can also be applied to this class of problems.

9.2. APPLICATION OF HMM TO STOCHASTIC SIMULATION ALGORITHMS405

9.2 Application of HMM to stochastic simulation al-

gorithms

First, let us review brieﬂy the standard stochastic simulation algorithm (SSA) for

chemical kinetic systems proposed in [20, 19], also known as the Gillespie algorithm.

This is closely related to the BKL algorithm in statistical physics [6]. The general set up

for the stochastic chemical kinetic system was discussed in section 2.3.3. Suppose we are

given a chemical kinetic system with reaction channels R

= (a

, ν

), j = 1, 2, ··· , M

Let

a(x) =

j=1

(x). (9.2.1)

Assume that the current time is t

, and the system is at state X

. We perform the

following steps:

1. Generate independent random numbers r

and r

with uniform distribution on the

unit interval (0, 1]. Let

δt

n+1

= −

ln r

a(X

)

, (9.2.2)

and let k

n+1

be the natural number such that

a(X

)

n+1

−1

j=0

) < r

≤

a(X

)

n+1

j=0

), (9.2.3)

where a

= 0 by convention.

2. Update the time and the state of the system by

n+1

= t

+ δt

n+1

, X

n+1

= X

+ ν

n+1

. (9.2.4)

Then repeat.

In this algorithm, r

is used to update the clock and r

is used to select the particular

reaction to be executed.

As we explained in section 2.3.3, in practice, the reaction rates often have very dis-

parate magnitudes. This can be appreciated from the reaction rate formula from tran-

sition state theory (see next chapter): The rates depend exponentially on the energy

barrier. Therefore a small diﬀerence in the energy barrier can result in a large diﬀerence

406 CHAPTER 9. PROBLEMS WITH MULTIPLE TIME SCALES

in the rate. In such a case, we are often interested more in the slow reactions since

they the bottlenecks for the overall dynamics. A t heory for the eﬀective dynamics was

described in section 2.3.3. However, it might be quite diﬃcult to compute the eﬀective

reaction rates in the eﬀective dynamics either analytically or by precomputing. There-

fore various strategies have been proposed to capture the eﬀective dynamics of t he slow

variables “on-the-ﬂy”. We will discuss an algorithm proposed in [12] which is a simple

modiﬁcation of the original SSA, by adding a nested structure according to the time scale

of the rates. The process at each level of the time scale is simulated with an SSA with

some eﬀective rates. Results from simulations on fast time scales are used to compute

the rates for the SSA at slower time scales. For simple systems with only two time scales,

the nested SSA consists of two SSAs organized with one nested in the other: An outer

SSA for the slow reactions only, but with modiﬁed slow rates which are computed in an

inner SSA modeling fast reactions only.

Let t

, X

be the cu rrent time and state of the system respectively. The two-level

nested SSA proceeds as follows:

1. Inner SSA: Pick an integer N. Run N independent replicas of SSA with the

fast reactions R

= {(ε

−1

, ν

})} only, for a time interval of T

+ T

. During this

calculation, compute the modiﬁed slow rates for j = 1, ··· , M

˜a

k=1

)dτ, (9.2.5)

where X

is the result of the k-th replica of this auxiliary virtual fast process at

virtual time τ whose initial value is X

t=0

= X

, and T

is a parameter we choose

in order to minimize the eﬀ ect of the transients to the equilibrium in the virtual

fast process.

2. Outer SSA: Run one step of SSA for the modiﬁed slow reactions

= ( ˜a

, ν

)

to generate (t

n+1

, X

n+1

) from (t

, X

Then repeat.

In the HMM language, the macro-scale solver is the outer SSA, the data that need

to be estimated is the eﬀective rates for the slow reactions. These data are obtained by

simulating the virtual fast process which plays the role of the micro-scale solvers here.