Weinan E. Principles of Multiscale Modeling
Подождите немного. Документ загружается.


4.4. ELECTRONIC STRUCTURE MODELS 197
The Hartree-Fock approximation is the solution to the variational problem:
inf
{ψ
i
}
I
HF
({ψ
i
}) (4.4.21)
subject to the orthonormality constraint (4.4.19). Obviously, the Hartree-Fock approxi-
mation gives an upper bound of the energy of the many-body system.
The Euler-Lagrange equations of (4.4.20) can be written as
Hψ
i
(x) −
X
j
Z
R
3
ψ
j
(x)ψ
i
(y)ψ
∗
j
(y)
|x − y|
dy = ε
i
ψ
i
(x), , i = 1, ··· , N (4.4.22)
where
H = −
1
2
∆ + V
ext
(x) +
Z
R
3
ρ(y)
|x − y|
dy, (4.4.23)
with the density ρ defined as
ρ(x) =
N
X
i=1
|ψ
i
(x)|
2
. (4.4.24)
The term
X
j
Z
R
3
ψ
j
(x)ψ
i
(y)ψ
∗
j
(y)
|x − y|
dy (4.4.25)
is called the exchange term, since it comes from the antisymmetry of the wave function.
For a mathematical introduction of the Hartree-Fock model, we refer the readers to [31].
4.4.3 Density functional theory
Density functional theory is an alternative approach for describing the electronic
structure of matter [21, 26, 34]. Its original motivation is to use only the density of
the electrons, rather than the wave functions, as the basic object for describing the
electronic structure of matter (at its ground state). Given the N-body wave function Ψ
e
,
the electron density is defined by:
ρ(x) = N
Z
|Ψ
e
(x, x
2
, . . . , x
N
)|
2
dx
2
. . . dx
N
(4.4.26)
which is the probability of finding an electron at point x. At a first sight, it seems
quite impossible to describe the electronic structure of an arbitrary system just by the
electron density, since ρ seems to contain much less information than the many-body

198 CHAPTER 4. THE HIERARCHY OF PHYSICAL MODELS
wave function. However, we should note that both the wave function and the density are
very much constrained by the fact that they are associated with the ground state of some
Hamiltonian operator. In fact, Hohenberg and Kohn showed that there is a one-to-one
correspondence between the external potential of an electronic system and the electron
density of its ground state [21], provided that the ground state is n ondegenerate. Since
the external potential determines the entire system, the ground state wave function
and hence the ground state energy is uniquely determined by the ground state electron
density. Indeed, not only the total energy, all the energy terms, such as the kinetic energy
and Coulomb interaction energy, are uniquely determined by the ground state electron
density. They can be expressed as universal functionals of the ground state electron
density.
Instead of discussing the details of the Hohenberg-Kohn theorem, it is more convenient
for us to introduce the formulation of the Levy-Lieb constrained variational problem.
Imagine solving the variational problem (4.4.13) in two steps: First we fix a density
function ρ and minimize the functional I over all wave functions whose density is ρ, and
we then minimize over all ρ. More precisely, define the functional
F (ρ) = inf
Ψ7→ρ
hΨ|H
e
|Ψi = hΨ| −
X
i
1
2
∆
x
i
+ V
ee
|Ψi, (4.4.27)
where the constraint Ψ 7→ ρ means that ρ is equal to the density given by Ψ using
(4.4.26). Ψ is also assumed to be anti-symmetric.
The ground energy of the system can now be expressed as:
E = inf
ρ
(F (ρ) +
Z
V
ext
ρ dx). (4.4.28)
The functional F contains the kinetic energy of the electrons and Coulomb interaction
between the electrons. F is a universal fun ctional, in the sense that it does not depend
on the external potential V
ext
. However, the explicit form of F is not known, and further
approximations are necessary in order to make this formulation useful in practice.
Kohn-Sham density functional theory
The first step, made by Kohn and Sham [26], is to restrict Ψ in (4.4.27) to the form
of a Slater determinant (4.4.18), where the the one-body wave functions {ψ
1
, . . . , ψ
N
}
satisfy the orthonormality constraints (4.4.19). This is similar in appearance to the
Hartree-Fock approximation, but the underlying philosophy is quite different. In the
4.4. ELECTRONIC STRUCTURE MODELS 199
Hartree-Fock approximation, we aim at obtaining an upper bound of t he energy by
restricting the form of the many-body wave function. Here we are mapping the system
to a virtual system of non-interacting electrons (i.e. whose wave function is given by a
Slater determinant), with an effective potential carefully chosen so that the density of
the electrons is the same as the density of the system we are interested in. The question
reduces to the choice of this effective potential. To see this, we first compute the energy
of a system of non-interacting electrons. Since
hΨ| −
X
i
1
2
∆
x
i
+ V
ee
|Ψi =
N
X
i=1
Z
R
3
1
2
|∇ψ
i
(x)|
2
+
1
2
ZZ
R
3
×R
3
ρ(x)ρ(y)
|x − y|
dx dy
−
1
2
N
X
i,j=1
ZZ
R
3
×R
3
ψ
∗
i
(x)ψ
i
(y)ψ
∗
j
(y)ψ
j
(x)
|x − y|
dx dy, (4.4.29)
the error made by neglecting electron-electron interaction is given by:
E
c
(ρ) = F (ρ) − inf
{ψ
i
}7→ρ
N
X
i=1
Z
R
3
1
2
|∇ψ
i
(x)|
2
dx +
1
2
ZZ
R
3
×R
3
ρ(x)ρ(y)
|x − y|
dx dy
−
1
2
N
X
i,j=1
ZZ
R
3
×R
3
ψ
∗
i
(x)ψ
i
(y)ψ
∗
j
(y)ψ
j
(x)
|x − y|
dx dy
. (4.4.30)
Here {ψ
i
} 7→ ρ means that ρ(x) =
P
i
|ψ
i
(x)|
2
. This is called t he correlation energy. Note
that it is a functional of ρ.
The last term on the right hand side of (4.4.30) will give a nonlocal potential in the
Euler-Lagrange equation as we have discussed in the Hartree-Fock approximation. This
is sometimes unpleasant, and one replaces it by an explicit functional of ρ, called the
exchange energy:
E
x
(ρ) =F (ρ) − inf
{ψ
i
}7→ρ
N
X
i=1
Z
R
3
1
2
|∇ψ
i
(x)|
2
dx − E
c
(ρ) −
1
2
ZZ
R
3
×R
3
ρ(x)ρ(y)
|x − y|
dx dy.
(4.4.31)
E
x
is also a functional of ρ. Define the exchange-correlation energy,
E
xc
(ρ) = E
x
(ρ) + E
c
(ρ), (4.4.32)
we can write
F (ρ) = T (ρ) +
1
2
ZZ
R
3
×R
3
ρ(x)ρ(y)
|x − y|
dx dy + E
xc
(ρ). (4.4.33)

200 CHAPTER 4. THE HIERARCHY OF PHYSICAL MODELS
Here T (ρ) is the new kinetic energy functional
T (ρ) = inf
{ψ
i
}7→ρ
N
X
i=1
Z
R
3
1
2
|∇ψ
i
(x)|
2
dx (4.4.34)
Notice that up to this point, what we have done is just a reformulation of the original
many-body problem – no approximations have been made. We still do not know the form
of E
x
(ρ) and E
c
(ρ), which account for the error made by approximating the many-body
wave funct ion using a single Slater determinant, and approximating the electron-electron
Coulomb interaction by the Hartree energy
E
H
(ρ) =
1
2
ZZ
R
3
×R
3
ρ(x)ρ(y)
|x − y|
dx dy (4.4.35)
The main insight of Kohn and Sham [26] is that by approximating the kinetic energy
using the one-body wave functions, one takes care of a large portion of the kinetic energy.
The remaining contribution is small and can be approximated with acceptable accuracy
using simple ideas, such as the local density approximation (LDA):
E
xc
(ρ) =
Z
ǫ
xc
(ρ(x)) dx, (4.4.36)
where ǫ
xc
(ρ) is a local function (rath er than a functional) of ρ, to b e modeled. For
example, for homogeneous free electron gas, its exchange energy can b e easily calculated
and is given by [34]:
E
x
= −C
D
V ρ
4/3
, (4.4.37)
where V is the volume C
D
is some universal constant. Based on this, it is assumed that
for systems close to homogeneous electron gas, the exchange energy can be approximated
as
E
x
(ρ) = −C
D
Z
ρ(x)
4/3
dx (4.4.38)
in the spirit of the local density approximation. One can also put in local density gradients
in order to get better accuracy:
E
xc
(ρ) =
Z
ǫ
xc
(ρ(x), ∇ρ(x)) dx (4.4.39)
under the name of generalized gradient approximation (GGA) [33].

4.4. ELECTRONIC STRUCTURE MODELS 201
These approximate exchange-correlation functionals can often give satisfactory re-
sults in practical computations. However, in general, it is difficult to make systematic
corrections to improve the accuracy.
Under the approximations for the exchange-correlation energy, the Kohn-Sham energy
functional is given by
I
KS
(ρ) = T (ρ) +
Z
V
ext
ρ dx + E
xc
(ρ) +
1
2
ZZ
ρ(x)ρ(y)
|x − y|
dx dy (4.4.40)
where
1. T (ρ) is the universal kinetic energy functional for noninteracting electron gas.
2. V
ext
is the external potential, particularly, for the nuclei-electron system:
V
ext
(x) = −
X
I
Z
I
|x − R
I
|
.
3. E
xc
is the exchange-correlation energy, we will assume LDA or GGA approximations
so that it is an explicit functional of ρ.
4. The last term on the right hand side is called the Hartree energy.
Notice that we may also consider the energy functional defined in terms of the one-
body wave functions:
I
KS
({ψ
i
}) =
X
i
Z
1
2
|∇ψ
i
|
2
dx +
Z
V
ext
ρ dx + E
xc
(ρ) +
1
2
ZZ
ρ(x)ρ(y)
|x − y|
dx dy (4.4.41)
The formulation presented above treats every electron in the system in an equal foot-
ing. In practice, one often associates the core electrons with the nucleus and treats only
the valence electrons. This has a tremendous practical advantage, since the wave func-
tions associated with the core electrons typically have rapid variations and are therefore
difficult to compute numerically. In addition, they usually do not participate in binding
between atoms or chemical reactions. However, in doing so, we also have to represent
the effect of the nuclei differently, by introducing some effective potential, often called
the pseudo-potential [33]. We can then rewrite the Kohn-Sh am functional as
I
KS
(ρ) = T (ρ) + J(ρ) + E
xc
(ρ) (4.4.42)

202 CHAPTER 4. THE HIERARCHY OF PHYSICAL MODELS
where
J(ρ) =
1
2
ZZ
(ρ(x) − m(x))(ρ(y) − m(y))
|x − y|
dx dy (4.4.43)
m(x) is the background charge distribution due to the nuclei and the core electrons. It
usually takes the form
m(x) =
X
I
m
a,I
(x − R
I
)
where m
a,I
is the contribution from the I-th nucleus with its core-electrons and R
I
is
its position. Note that in the new form (4.4.42), the effect of the nuclei-nuclei Coulomb
interaction is included in the functional.
Thomas-Fermi and orbital-free density functional theory
In Thomas-Fermi theory, we model T [ρ] by considering the kinetic energy of a homo-
geneous free (i.e. n on-interacting) electron gas. This gives rise to [34]
T
T F
[ρ] = C
F
Z
ρ
5/3
(x)dx, (4.4.44)
where C
F
is an universal constant. This result is the consequence of a simple scaling
argument. Since we are considering homogeneous free electron gas, the end result can
only depend on the pointwise value of ρ (not on, for example, the gradient of ρ). Obviously
on dimensional grounds, we have [Ψ]
2
= [ρ], [ρ] = 1/L
3
where L denotes the dimension
of length. Therefore we have
[|∇Ψ|
2
] = [ρ]/L
2
= [ρ]
5/3
and this gives (4.4.44).
The simplicity of the Thomas-Fermi theory comes with a big price: The Thomas-
Fermi model does not allow binding between atoms. Indeed the well-known Teller’s
theorem states that if we divide a neutral electronic system (i.e. total charge vanishes)
into two disjoint neutral subsystems, then within the Thomas-Fermi theory, the total
energy is a decreasing function of the distance between the two subsystems [34].
Many ideas have been proposed to remedy this problem. One well-known example is
the Thomas-Fermi-von Weizs¨acker (TFW) model
T
T F W
[ρ] = T
T F
[ρ] + λ
Z
|∇ρ|
2
ρ
dx. (4.4.45)
where λ is some parameter. The TFW model does allow binding between atoms.
4.4. ELECTRONIC STRUCTURE MODELS 203
The second idea is to add integral terms. The most well-known example of such a
functional is the Wang-Teter functional [7]
T
W T
[ρ] = T
T F W
[ρ] +
Z Z
ρ
5/6
(x)K
W T
(x, y)ρ
5/6
(y)dxdy. (4.4.46)
Here K
W T
is a kernel function, constructed in order to reproduce accurately the linear
response of a homogeneous free electron gas, given by the Lindhard function [7].
4.4.4 Tight-binding models
Tight-binding models (TBM) are th e simplest electronic structure models with explicit
wave functions. They are the minimalist type of models, based on
1. representing the wave functions using a minimum basis set, often in the form of
atomic orbitals which are the ground and excited states for the electron in the
hydrogen atom, and
2. neglecting electron-electron interaction except that the Pauli exclusion principle is
still imposed.
Under these approximations, the state space becomes finite and the Hamiltonian operator
becomes a matrix. This makes it possible to carry out explicit analytical calculations
as well as efficient numerical computations. Even though TBM is quite crude, it is very
useful as a theoretical and practical tool. Its accuracy can be improved to some extend
by calibrating the matrix elements of the Hamiltonian against results from more accurate
models.
Let us start with the example of a hydrogen ion H
+
2
. To set up the coordinates, we
put the two atoms on the real axis, see Figure 4.6. The wave function Ψ is expressed as
a linear combination of a minimal set of atomic orbitals:
Ψ = c
1
ϕ
1
+ c
2
ϕ
2
(4.4.47)
where ϕ
1
is the 1s orbital of atom 1, and ϕ
2
is the 1s orbital of atom 2 (see [24]). The
Hamiltonian operator is of the form:
H = T + V
1
+ V
2
(4.4.48)

204 CHAPTER 4. THE HIERARCHY OF PHYSICAL MODELS
where T is the kinetic energy operator, V
1
and V
2
are the Coulomb potential associated
with atoms 1 and 2 respectively. We will discuss the explicit form of H later. Our
problem is then reduced to the eigenvalue problem
HΨ = εΨ (4.4.49)
for finding c
1
, c
2
and ε.
Figure 4.6: S etup of the tight-binding model for the analysis of the binding of two atoms.
Taking inner product of ( 4.4.49) with respect to ϕ
1
and ϕ
2
respectively, we get
(ϕ
1
, HΨ) = ε(ϕ
1
, Ψ) (4.4.50)
(ϕ
2
, HΨ) = ε(ϕ
2
, Ψ)
We can express this equation in a matrix form:
H
c
1
c
2
= εS
c
1
c
2
(4.4.51)
where
H =
H
11
H
12
H
21
H
22
!
=
(ϕ
1
, Hϕ
1
), (ϕ
1
, Hϕ
2
)
(ϕ
2
, Hϕ
1
), (ϕ
2
, Hϕ
2
)
!
(4.4.52)
S =
S
11
S
12
S
21
S
22
!
=
(ϕ
1
, ϕ
1
), (ϕ
1
, ϕ
2
)
(ϕ
2
, ϕ
1
), (ϕ
2
, ϕ
2
)
!
are the Hamiltonian and mass matrices respectively.
Next we discuss how the elements of these two matr ices can be app roximated. In
orthorgonal TBM, the overlapping integral between the different atomic orbitals are ne-
glected: (ϕ
1
, ϕ
2
) ∼ 0, and S is approximated by the identity matrix. For the Hamiltonian

4.4. ELECTRONIC STRUCTURE MODELS 205
matrix,
H
11
= hϕ
1
|T + V
1
+ V
2
|ϕ
1
i (4.4.53)
= hϕ
1
|T + V
1
|ϕ
1
i + hϕ
1
|V
2
|ϕ
1
i (4.4.54)
= ε
0
1s
+ ∆ (4.4.55)
= ε
s
(4.4.56)
ε
s
is called the on-site energy. ε
0
1s
= hϕ
1
|T + V
1
|ϕ
1
i is the en ergy of the 1s state of the
hydrogen atom.
H
12
= hϕ
1
|T + V
1
+ V
2
|ϕ
2
i (4.4.57)
= hϕ
1
|T + V
1
|ϕ
2
i + hϕ
1
|V
2
|ϕ
2
i
= ε
0
1s
(ϕ
1
, ϕ
2
) + hϕ
1
|V
2
|ϕ
2
i
≈ hϕ
1
|V
2
|ϕ
2
i = −t < 0
The last equation defines the parameter t. Since ϕ
1
and ϕ
2
are positive, V
2
is negative,
t is positive. The values of ε
s
and t depend on the distance between the two ions. Their
expression can be obtained empirically with input from results of more accurate models.
To summarize, we can write H as
H =
ε
s
−t
−t ε
s
!
(4.4.58)
The eigenvalues for this matrix are
ε
+
= ε
s
− t < ε
s
(4.4.59)
ε
−
= ε
s
+ t
with the corresponding eigenvectors:
Ψ
+
=
1
√
2
(ϕ
1
+ ϕ
2
) (4.4.60)
Ψ
−
=
1
√
2
(ϕ
1
− ϕ
2
)
Ψ
+
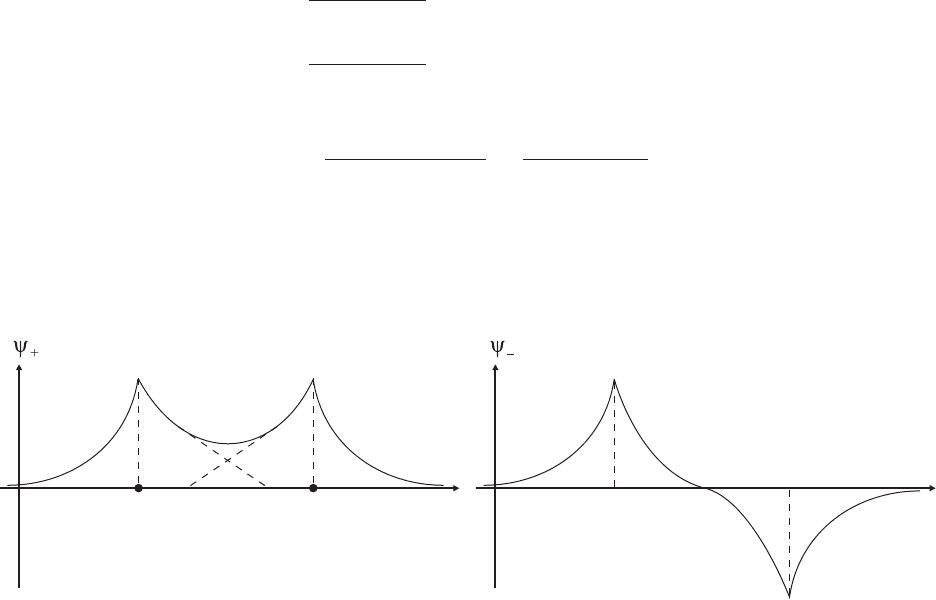
is the bonding state: an electron in this state has a higher probability to be found
between the two nuclei. Ψ
−
is the anti-bonding state, see Figure 4.7.
206 CHAPTER 4. THE HIERARCHY OF PHYSICAL MODELS
If we take into account the overlap, then Ψ
+
and Ψ
−
are still the eigenvectors, but
the eigenvalues change to:
ε
+
=
hΨ
+
|H|Ψ
+
i
hΨ
+
|Ψ
+
i
= ε
s
+ V
ssσ
− hϕ
1
|ϕ
2
iV
ssσ
(4.4.61)
ε
−
=
hΨ
−
|H|Ψ
−
i
hΨ
−
|Ψ
−
i
= ε
s
− V
ssσ
− hϕ
1
|ϕ
2
iV
ssσ
(4.4.62)
where
V
ssσ
=
H
12
− hϕ
1
|ϕ
2
iε
s
1 − hϕ
1
|ϕ
2
i
2
=
hϕ
1
|V
2
|ϕ
2
i
1 − hϕ
1
|ϕ
2
i
2
< 0 (4.4.63)
The first term at the right hand side of (4.4.61) is the on-site energy. The second term
is negative, corresponding to an attractive interaction. The third term is only important
when there is significant overlap, i.e. at short distance. This is a repulsive term.
Figure 4.7:
Figure 4.8: Bonding (left) and anti-bonding (right) states
Next we consider the problem of a one-dimensional chain of N lithium atoms. We
will use the periodic boundary condition. We denote by x
j
the position of the j-th
atom, x
j
= ja where a is the distance between neighboring atoms. The wave function is
represented as a linear combination of the 1s orbitals of the atoms:
Ψ =
N
X
j=1
c
j
ϕ
j
(4.4.64)
where ϕ
j
is the 1s orbital of the j-th atom. Again for simplicity, we will use the orthorg-
onal TBM. For the Hamiltonian matrix we will use the nearest neighbor approximation.
